Ces documents sont disponibles en version pdf et postscript (plus court à télé-charger). Pour lire les version pdf, si vous n'avez pas Acrobat Reader, vous pouvez le télé-charger gratuitement en cliquant sur l'icône ci-contre.

Ressources du site CultureMath

Sites externes

  Résumés

Combinatoire, dénombrement :

• Les colliers de G. Polyà

  Il est ici question d'un théorème peu connu de G. Polyà, résultat qui fournit une méthode systématique pour dénombrer les coloriages possibles d'un ensemble sous l'action d'un groupe. De tels problèmes peuvent être posés de façon extrêmement simple : par exemple, combien peut-on faire de colliers différents si l'on dispose de 10 perles noires et de 3 perles rouges ? (par Thomas Chomette)
  

  Prérequis :

  • Quelques notions élémentaires de théorie des groupes (définition d'une action de groupe, du groupe des transformations d'une figure). Fiche de rappels disponible au format ps ou pdf.
  • Savoir manipuler des expressions algébriques un peu élaborées (sommes de produits...)

Importer l'article en version ps ou pdf.

Pour revenir au sommaire :

Un problème de digicode

Un peu de théorie des graphes, où comment venir à bout d'un digicode plus vite que n'importe qui. Nous nous intéressons ici à la question de savoir combien de chiffres il faut taper successivement sur un digicode pour être sûr d'avoir tapé toutes les combinaisons possibles. Il s'avère que cette question se modélise de façon agréable dans le langage des graphes orientés, et que l'on peut alors résoudre notre problème initial. Nous voyons enfin quelques applications classiques du résultat de théorie des graphes utilisé. (par Thomas Chomette)

Prérequis :

Aucun, si ce n'est une idée intuitive de ce qu'est un graphe. Tous les objets nécessaires à la résolution de notre problème sont définis, mais il est bon de pouvoir s'en faire une image mentale.

Importer l'article en version ps ou pdf.

Pour revenir au sommaire :

Graphes planaires

À quelle condition peut-on dessiner un graphe dans le plan, sans que ne se croisent des arêtes dudit graphe ? Le problème est assez classique : on connaît des condition nécessaires, qui dérivent de la formule d'Euler. Nous introduisons ici ces résultats, en montrant quelques applications sur des graphes particuliers. Il existe également une caractérisation exacte, dûe au mathématicien Polonais Kuratovsky, que nous présentons à la fin de ce texte. (par Thomas Chomette)

Prérequis :

Aucun.

Importer l'article en version ps ou pdf.

Pour revenir au sommaire :

Combien de rangements possibles ?

Nous allons nous intéresser ici au nombre de manières de ranger des boules dans des boîtes. Problème classique s'il en est : nombre d'arrangements, nombre de combinaisons... Contrairement aux apparences, ce problème n'est pas toujours si simple lorsque l'on s'impose comme ici une contrainte supplémentaire : les boîtes sont indistinguables les unes des autres. Là, les choses se compliquent !
Dans le cas où les boules sont, elles numérotées, on arrive à dire pas mal de choses : d'abord, on peut établir une formule explicite pour le nombre de façons de ranger n boules dans k boîtes. Et l'on détermine alors le comportement asymptotique de cette suite... Le cas des boules elles-mêmes indistinguables est plus complexe, on se contentera d'une formule de récurrence et d'un équivalent. (par Arvind Singh, ENS)

Prérequis :

Manipulation d'expressions algébriques complexes, de suites définies de manière récurrente.

Ordres de grandeur sur les suites (suites équivalentes, négligeables l'un par rapport à l'autre).

Pour la partie 1.5 : développements en série, développements limités, notations exponentielles.

Importer l'article en version ps ou pdf.

Pour revenir au sommaire :

Du Triangle de Pascal aux Séries Formelles

Les suites de Fibonacci, le nombre de parenthésages “légaux” possibles avec 2n parenthèses, le profil des montagnes... Ces sujets on un rapport, dans le monde des mathématiques !

Il existe en effet une manière assez générale d'étudier des suites dont la définition fait apparaître (clairement ou après analyse), des phénomènes de récurrence. Il s'agit d'introduire une série formelle associée à cette suite. Le but de ce texte est d'introduire cette notion qui généralise celle de polynôme en autorisant les degrés infinis.

Nous verrons que cet objet algébrique permet d'effectuer des manipulations combinatoires sans passer par le traitement analytique de la notion de somme infinie. Nous verrons également que ces manipulations doivent être effectuées avec prudence, et uniquement dans un cadre clairement établi.

Par Farouk Boucekkine, ENS.

Prérequis :

Manipulation d'expressions algébriques complexes, de suites définies de manière récurrente.

Fractions rationnelles (définition)

Cardinal d'un ensemble (combinatoire niveau terminale)


Importer l'article en version ps ou pdf.

Pour revenir au sommaire :

 

Montagnards et polygones

Voici un texte qui nous a été envoyé par un de nos jeunes lecteurs, Thibault Bourgeron, actuellement en classe de terminale S au lycée Sainte-Marie d'Antony ! Ce travail traite de deux problèmes à résoudre par récurrence.

Le premier vous est peut-être familier, puisqu'il s'agit de voir combien de contours de montagnes on peut imaginer avec n montées et n descentes (Thibault, lecteur assidu de CultureMATH, a lu notre article sur les chemins de Dyck, et nous a donc envoyé son travail, avec l'accord de ses professeurs).

Le second problème consiste à déterminer le nombre de manières de découper un polygone en triangles dont les sommets sont des sommets du polygone, et dont les arêtes ne se croisent pas.

Ce texte a été produit pendant son année de première S dans le cadre du club Maths-en-Jeans de son lycée, jumelé avec celui du lycée Blaise Pascal d'Orsay, sous le patronage des professeurs de mathématiques Guillaume Gervet et Marie-dominique Mouton, et de deux doctorantes, Sophie Donnet et Marie Sauvé. Outre Thibault, trois élèves ont participé à sa rédaction, Michaël Beniluz, Yves Desclercs et Alice Magnaudet (à l'époque tous en première S).

Prérequis :

Manipulation d'expressions algébriques complexes, de suites définies de manière récurrente.

Fractions rationnelles (définition)

Cardinal d'un ensemble (combinatoire niveau terminale)


Importer l'article en version ps ou pdf.

Pour revenir au sommaire :

Imparité rythmique

Par André Bouchet

Résumé -  L’ethnomusicologue Simha Arom a observé une structure rythmique asymétrique utilisée entre autres par les Pygmées Aka de la vallée de la Lobaye, République centrafricaine.
La propriété caractéristique de ces formules rythmiques, l’imparité rythmique, a été étudiée par Marc Chemillier (Mathématiques de la musique d’Afrique centrale, CultureMATH, 2009).
Cet article propose une nouvelle approche de cette propriété et en donne un théorème de caractérisation.

Lire l'article

Pour revenir au sommaire :

Arithmétique, théorie des nombres :

L'Algorithme de Génération des Premiers (AGP)

Résumé- Cet article décrit un algorithme qui propose un point de vue nouveau sur la génération des nombres premiers. On l’appellera Algorithme de Génération des Premiers ou AGP.

Utilisation en classe -  Ce texte offre un exemple original  d'algorithme. La description de l'algorithme AGP est accessible à un élève de seconde. Quant aux lois mathématiques de l'AGP, elles pourraient être abordées en terminale S ou en classe préparatoire. Une version courte en anglais offre une ressource pertinente pour des classes de sections européennes  "maths-anglais".

Lire l'article

Lire la version anglaise - The Prime-Generating Algorithm (PGA)

Pour revenir au sommaire :

Arithmétique

Marc Hindry, professeur à l’Université Paris Diderot (Paris 7), membre de l’équipe de Théorie des Nombres de l’Institut de Mathématiques de Jussieu. Résumé - A l'occasion de la sortie de son livre "Arithmétique" aux éditions Calvage et Mounet (2008), Marc Hindry a bien voulu répondre aux questions de CultureMmath. Dans cette conversation à bâtons rompus, il nous parle de son travail de mathématicien et d'enseignant et nous entraîne sur les traces de Fermat, Euler, Gauss, Dirichlet, Riemann et bien d'autres. Lire l'article

Voir aussi: Points rationnels et courbes elliptiques de Jérôme Gärtner.

Pour revenir au sommaire :

Points rationnels et courbes elliptiques

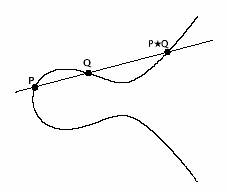
Jérôme Gärtner, Ecole Normale Supérieure de Cachan et Institut de mathématiques de Jussieu (Université Paris 6, Pierre et Marie Curie) Résumé - Le but de cet article est d'introduire à deux notions utilisées actuellement dans la recherche en théorie des nombres : les points rationnels et les courbes elliptiques. On y trouvera en premier lieu une explication de l'intérêt porté aux points rationnels, en lien avec le théorème de Pythagore. Ensuite, après avoir expliquer la notion de loi de groupe sur les points rationnels d'une courbe elliptique, on énonce un résultat important, le théorème de Mordell- Weil. La fin de l'article est consacrée à la manière dont ces notions interviennent dans la recherche actuelle, autour de deux exemples : un problème ouvert, la conjecture de Birch et Swinnerton-Dyer, et les points de Heegner. On trouvera en conclusion un panorama des notions relatives aux courbes elliptiques en lien avec la théorie des nombres, ainsi qu'une bibliographie détaillée. Le niveau requis est le bagage classique d'un étudiant de premier cycle (un petit peu de géométrie, et la définition d'un groupe). Importer l'article (pdf - 14 pages - 225 Ko)

Voir aussi: Arithmétique, entretien avec Marc Hindry.

Pour revenir au sommaire :

Problème des bœufs du soleil

250 ans avant notre ère le savant Archimède (né et mort à Syracuse, ville de Sicile) proposait à Eratosthène de Cyrène, le problème du troupeau du Soleil dont le texte en grec a été retrouvé par Gotthold Ephreim Lessins et publié en 1773. Ce texte publié en grec dans le tome III du livre "Archimède" de Charles Mugler (Société d'édition "les belles Lettres" 1971), numérisé par l'auteur ici; il est également accessible en ligne.

L'article donne la traduction en français de l'énoncé d'Archimède et détaille les calculs menant à "la" solution. Celle-ci utilise toutes les finesses de l'arithmétique, de l'algèbre des corps finis, en utilisant aussi la théorie des fractions continues pour solutionner l'équation de Pell-Fermat, clef du problème. L'effectif minimal du troupeau du Soleil est un nombre de 206 545 chiffres, qui occupent 60 pages à l'impression (serrée) et qui commence à gauche par 7760 et se termine par 1800 (pour voir ce nombre cosmique, cliquer ici).

Le lecteur pourra trouver la procédure, en Maple ici, ou bien sur le web, par exemple sur le site de Philippe Dumas de l'Inria qui donne également de multiples liens. Ce même lecteur trouvera d'autres liens par Google en demandant : troupeau du Soleil Archimède ou les sites anglophones par cattle of the Sun, par exemple celui-ci.

Par Lazare Georges Vidiani, Professeur de Mathématiques.

Importer l'article (version pdf, 6 pages, 202 Ko)

Pour revenir au sommaire :

Le problème des nombres gelés de Saint-Exupéry

Dans le numéro spécial 12-14 de la revue Confluences 1947, numéro spécial consacré à Antoine de Saint Exupéry, dans le chapitre "voyage de l'Universel", écrit par le général Chassin, qui fut le chef de Saint-Exupéry, ce problème est évoqué, annoncé situé dans les annexes où il ne figure pas !   Après une traque de trois ans et huit mois, l'auteur a réussi à retrouver son énoncé, et en donne une solution, en rappelant le problème célèbre du Pharaon.

Merci à Mr Fabien Petitjean pour ses corrections.

Par Lazare Georges Vidiani, Professeur de Mathématiques.

Importer l'article (version pdf, 5 pages, 131 Ko)

Pour revenir au sommaire :

• Quelques résultats et conjectures de transcendance

  Nous présentons ici un panorama des résultats et conjectures les plus classiques autour de la notion de transcendance. Ce n'est bien sûr pas une revue exhaustive de l'état de la recherche dans ce domaine, mais les problèmes dont il est ici question, quoique simples dans leur formulation, restent au coeur des préoccupations actuelles. (d'après Stéphane Fischler, ENS Ulm)
  

  Prérequis :

  • Quelques notions d'arithmétique (lemme de Gauss, décomposition en facteurs premiers).
  • Exponentielle et logarithme complexe (une vague connaissance de ces fonctions suffit).
  • Un peu d'algèbre linéaire (familles libres et familles liées).

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• Sur l'algorithme RSA

  L'algorithme RSA, inventé en 1978, est plus que jamais d'actualité, puisqu'il reste 20 ans plus tard la cheville ouvrière de nombreux protocoles de cryptographie utilisés pour la transmission de tout type de données. Il est basé sur un principe d'inversion modulo un très gros nombre, lui-même produit de deux très gros nombres premiers.
  Nous expliquons ici le protocole ainsi que les principes d'arithmétique qu'il utilise, tout en nous intéressant également aux problèmes pratiques de sa mise en oeuvre, qui nécessite de savoir manipuler rapidement de très gros entiers, et a donc besoin d'algorithmes performants. (d'après François Maurel, Paris VII)
  

  Prérequis :

  • Bases de l'arithmétique (ce texte se veut auto-suffisant, mais une certaine familiarité avec les raisonnement d'arithmétique aident à sa compréhension).

  Importer l'article en version ps ou pdf.
  

Pour revenir au sommaire :

• Une démonstration originale de l'infinité de l'ensemble des nombres premiers

  La démonstration la plus classique de ce résultat, par l'absurde, qui consiste à exhiber un nombre premier à tous les autres, est certes très élégante, mais assez contre-intuitive. Comment y penser si on ne la connaît pas déjà ?
  Celle que nous présentons ici, sans être radicalement différente, semble plus naturelle. Il s'agit de savoir ce qui se passerait si l'ensemble des nombres premiers était fini. On arrive alors assez vite à un problème pour décomposer tous les entiers en facteurs premiers : à partir d'un certain rang, il y aura des trous ! (d'après Joël Bellaiche, ENS Ulm, avec une contribution d'Yves Mulet Marquis, ingénieur électronicien)
  

  Prérequis :

  • Décomposition en facteur premiers.
  • Comportement asymptotique de la fonction logarithme.

   

  Importer l'article en version ps ou pdf.
  Pour revenir au sommaire :

• Approximation diophantienne et réseaux

  La théorie de l'approximation diophantienne est l'étude des propriétés d'approximation de nombres par des rationnels. Elle intervient dans de nombreux domaines des mathématiques. Nous présentons ici quelques premiers résultats d'approximation par des rationnels, en traitant d'abord le cas d'un seul réels, puis de plusieurs ou, ce qui revient au même, d'un vecteur dans un espace vectoriel réel de dimension finie. (par Benoît Mselati, ENS)
  

  Prérequis :

  • Manipulation de suites.
  • Mesure de Lebesgue (seule la mesure d'un pavé et la propriété d'additivité finie de la mesure sont ici utilisés)
  • Calcul matriciel : multiplication, inversion.
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• Fermat revisité

  Le "petit théorème de Fermat" est un bijou de simplicité et d'utilité. Depuis sa découverte il y a plus de 400 ans par Fermat, on l'a redémontré d'au moins 100 manières différentes !

  Dans ce texte, à la limite des programmes d'arithmétique de terminale scientifique, nous vous proposons de (re)découvrir ce petit joyau sous plusieurs points de vue, ainsi que des applications (Wilson) et des réciproques partielles.

  Par Géry Huvent, Michel Gouy et Alain Ladureau, dans le cadre de l'IREM de Lille.
  

  Prérequis :

  • Aucun, une habitude des manipulations de congruences est toutefois utile (des rappels sont proposés au début du texte).
  
  

  Importer l'article entier au format ps ou pdf.

Probabilités et statistiques :

• Combien de fois faut-il battre un jeu de cartes ?

  Lorsque l'on bat un jeu de cartes, selon le procédé classique qui consiste à couper le paquet en deux parties puis à alterner les cartes des deux parties pour reformer un seul tas (puis à recommencer l'opération un certain nombre de fois), le but est bien sûr qu'aucun joueur ne puisse deviner l'ordre des cartes après battage. Manifestement, si l'on ne bat qu'une seule fois, un joueur attentif qui connaissait l'ordre initial des cartes dispose encore de certaines informations. D'où la question de savoir combien de fois il faut battre le paquet de cartes pour qu'il soit "bien mélangé".
  Nous introduisons ici un modèle probabiliste de l'opération de battage, et nous étudions les probabilités des différents ordres possibles des cartes après un nombre de battages donné. Puis nous nous posons la question de savoir à partir de combien de battages on peut considérer que la répartition est vraiment aléatoire, c'est-à-dire quand est-ce que la répartition des probabilités est (quasi) homogène. (par Philippe Biane, ENS/CNRS)
  

  Prérequis :

  • Manipulation de nombres de combinaisons et de factorielles.
  • Loi binomiale.
  • Probabilités conditionnelles, multiplicativité des probabilités.
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• Avant le référendum

  Les sondages d'opinions sont devenus partie intégrante de notre quotidien. Tout le monde sait comment ils sont effectués, dans les grandes ligne. Mais que signifient-ils exactement ? Quel crédit leur apporter ?
  En nous basant sur cet exemple fondamental, nous introduisons dans ce texte la notion d'inférence statistique, en essayant de la décortiquer au maximum. Notre but est en l'occurrence de définir ce que peut-être une marge d'erreur, un intervalle de confiance. (par Thomas Chomette, avec l'aide de Patricia Reynaud-Bouret, ENS)
  

  Prérequis :

  • Notion de variable aléatoire.
  • Manipulation d'expression algébriques.
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• La percolation

  La percolation est un phénomène physique que l'on rencontre bien sûr lorsque l'on étudie le passage de la vapeur à travers du café, mais également des situations aussi diverses que la propagation d'un incendie de forêt, la circulation automobile, la conductivité électrique d'une alliage...
  Nous introduisons ici cette théorie, partant de la notion de graphe aléatoire. Nous verrons notamment qu'il existe une notion de probabilité critique, c'est-à-dire un seuil tel qu'en-dessous la probabilité d'avoir un phénomène de percolation est nulle, et égale à 1 au-delà.
  Nous nous pencherons plus particulièrement sur les cas des arbres infinis et des réseaux cubiques.

  Par Clément Gallo, ENS Cachan. Texte issu d'un mémoire effectué au cours de la scolarité au département de mathématiques de l'ENS Cachan. Le texte intégral du mémoire est disponible ici.
  

  Prérequis :

  • Théorie de la mesure, probabilités :
    
    • Définition d'un espace de probabilité, d'une tribu, d'une mesure.
    • Espérance, probabilité d'un événement sous forme d'intégrale.
  • Manipulation de bornes supérieures, limites supérieures...
  • Propriétés élémentaires des graphes.
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• La corde de Bertrand

  Étant donné un cercle, si l'on trace une corde au hasard sur ce cercle, quelle est la probabilité pour que celle-ci soit plus longue que le rayon du cercle ?
  Cette question, connue sous le nom de "paradoxe" de la corde de Bertrand, est particulièrement judicieuse pour illustrer la notion de mesure de probabilité. Nous allons voir que la réponse varie en fonction du mode de construction, chaque façon de penser étant lié à une mesure particulière. (par Thomas Chomette, avec l'aide de Patricia Reynaud-Bouret, ENS)
  

  Prérequis :

  • Géométrie élémentaire.
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• Processus de branchement et descendance d'un individu.

  Les processus de branchement sont des modèles introduits pour étudier le développement d'une population, dans laquelle les individus se reproduisent indépendamment les uns des autres, et selon la même loi de probabilité. Introduit au 19ème siècle pour étudier la probabilité d'extinction de noms de familles illustres en Grande Bretagne, le modèle de Galton-Watson et ses variantes trouve de nombreuses applications en biologie ou en physique nucléaire. (par Thomas Chomette, avec l'aide de Vincent Beffara, ENS)
  

  Prérequis :

  • Manipulations élémentaires de séries entières (dérivation...) et de séries à termes positifs.
  • Probabilités conditionnelles, indépendance de variables aléatoires.
  • Convergence de suites récurrentes.
  • Propriétés classiques des fonctions convexes.
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• Marches aléatoires sur Z

  Quelle est la probabilité, lors d'un dépouillement, pour que le candidat majoritaire le soit tout au cours du dépouillement ? Quelle est la probabilité de ruine d'un joueur ? Combien faut-il de monnaie dans un caisse pour pouvoir servir tout le monde ? Voici quelques-unes des questions qui nous amènent à étudier la notion de marche aléatoire. Nous présentons donc ici un survol de résultats, très élémentaires au début, sur les marches aléatoires dans Z, l'ensemble des entiers relatifs. C'est ensuite l'occasion d'aborder un certain nombre de résultats assez classiques de probabilités. (par Thomas Chomette, avec l'aide de Yannick Baraud, ENS/CNRS).
  

  Prérequis :

  • Aucun pour la première partie.
  • Pour la seconde partie, on utilise assez régulièrement les propriétés des probabilités conditionnelles. Une certaine habitude des séries et des suites récurrentes est également souhaitable.
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• Le jeu de Pile ou Face

  Pierre et Paul jouent à pile ou face selon une règle simple. Pierre joue en premier, s'il tire Pile, il gagne. Sinon, c'est au tour de Paul qui tire deux fois et qui gagne s'il tire Pile au moins une fois. Si ce n'est pas le cas, Pierre joue à nouveau et tire trois fois, et ainsi de suite...

  Quelle est la probabilité que Pierre gagne ?

  Partant de ce problème concret, les auteurs développent des algorithmes permettant de simuler une longue partie de pile ou face, échaffaudent des conjectures et les démontrent par la suite. Un bon exemple à montrer à des élèves !

  Ce texte a été conçu dans le cadre du groupe de Calcul Formel de l'IREM de Lille par Géry Huvent, Michel Gouy et Alain Ladureau.
  
  

  Prérequis :

  • Aucun pour une grande partie du texte. Pour aller en profondeur, utilisation de suites récurrentes, séries pour quelques détails dans les preuves.
  • Le texte présente des algorithmes de calcul et des programmes, il est profitable mais non nécessaire de pouvoir les mettre en œuvre chez soi.
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• La statistique comme outil d'aide à la décision

  Un texte général (sans aspects techniques). Ce texte est le résumé d'un exposé fait par l'auteur devant les élèves du lycée Parc de Vilgenis (Massy) en mars 2004. Les statistiques sont une partie souvent mal connue des mathématiques, alors même qu'elle croise la réalité bien souvent, et ce texte tente d'en montrer les aspects peu connus sans entrer dans les détails. Nous proposerons un dossier mathématiquement plus complet sur le sujet au cours de l'année 2005.
  
  Par Gilles Stoltz, chercheur à l'ENS.

  Prérequis :

  • Aucun

  Lire l'article (html).

  Voir aussi

  • Information incomplète et regret interne en prédiction de suites individuelles, Gilles Stoltz
  • Les conférences filmées du groupe de travail "Apprentissages" sur le site de la "Diffusion des savoirs" de l'ENS
    • Optimal oracle inequality for aggregation of classifiers under low noise condition (le 12 juin 2006) — Guillaume Lecué
    • Groupe de lecture ’Fléau de la dimension’ (le 15 mai 2006) — Jean-Michel Marin
    • Vitesses minimales en dimension infinie dans le cadre du bruit blanc gaussien (le 3 avril 2006) — Patricia Reynaud-Bouret
    • Sélection de modèles par agrégation (le 20 mars 2006) — Jean-Yves Audibert
    • Obtention d’inégalités oracle exactes par méthodes de prédiction séquentielle (le 6 mars 2006) — Gilles Stoltz
    • Problèmes de classification à coûts asymétriques (le 20 février 2006) — Francis Bach - Conférence en français
    • Propriétés statistiques des espaces propres de l’analyse en composantes principales à noyau (le 30 janvier 2006) — Laurent Zwald
    • Estimation de modèles graphiques gaussiens (le 16 janvier 2006) — Nicolas Verzelen
    • Sélection itérative de caractéristiques en estimation de régression (le 28 novembre 2005) — Pierre Alquier
    • A propos de ’The Dantzig selector: Statistical estimation when p is much larger than n’ de Candes et Tao (le 14 novembre 2005) — Vincent Rivoirard
    • In search of graphical models (le 7 novembre 2005) — Guido Consonni
    • Consistency of one Class SVM and related algorithms (le 24 octobre 2005) — Régis Vert
    • Ouverture du groupe de lecture Fléau de la dimension (i.e., Curse of Dimensionality) (le 3 octobre 2005) — Pascal Massar

  Pour revenir au sommaire :

Géométrie :

Géométrie non arguésienne dynamique

Par Yves Martin, IUFM de la Réunion

Résumé - Lors de son axiomatisation de la géométrie euclidienne, dans ses Fondements de la géométrie, Hilbert a montré l’importance de la configuration de Desargues pour obtenir une géométrie affine. On appelle depuis “non arguésienne” une géométrie plane qui ne vérifie pas le théorème de Desargues. Le modèle le plus simple est le plan de Moulton (1902). En dehors de questions sur les fondements de la géométrie projective, avec les travaux Ruth Moufang vers 1933, la géométrie non arguésienne en général, et celle du plan de Moulton en particulier, n’ont jamais fait l’objet d’une étude spécifique, le traitement algébrique ne se prêtant pas à sa singularité. Mais depuis quelques années, les possibilités de modélisation des logiciels de géométrie dynamique récents permettent d’explorer cette géométrie sans difficulté. C’est ce que propose cet article. On y verra tout d’abord en quoi l’absence de la configuration de Desargues rend inopérant le concept de milieu quand il est considéré comme affine. Ensuite, la géométrie de Moulton vérifiant tous les autres axiomes de la géométrie euclidienne, nous pouvons effectuer des investigations sur les concepts d’angle, d’orthogonalité et de distance. Contrairement à la typologie associée aux angles pour les géométries usuelles (hyperboliques, euclidienne, elliptique) pour lesquelles la somme des angles triangles sont respectivement inférieure, égale ou supérieure à deux droit, dans le plan de Moulton, les 3 configurations se rencontrent. L’orthogonalité y est, elle aussi, est bien particulière puisque d’un point il peut ne pas passer de perpendiculaire à une droite donnée ou en passer deux – et deux seulement. La distance (ou semi distance selon les auteurs) n’est pas une métrique : l’inégalité triangulaire n’y est pas vérifié ce qui induit des résultats assez surprenants non seulement sur les triangles, mais aussi sur la distance d’un point à une droite.

Utilisation dans l'enseignement - Cette présentation simple d’une géométrie inhabituelle présente un grand intérêt pédagogique à plusieurs niveaux de l’enseignement. La simple manipulation des figures dynamiques peut permettre de faire sentir à des élèves de terminale ou à des étudiants de première année ce qu’est un système axiomatique. Dans un contexte de formation initiale des enseignants au sein d’un module de géométrie, mais aussi pour un questionnement didactique en formation continue, les figures de cet article sont l’occasion de travailler – outre les propriétés détaillées ci-dessus – le sens des axiomes de congruence, en particulier sur le fait qu’ils ne sont pas nécessairement liés à l’existence du mouvement dans la géométrie ainsi décrite. La géométrie de Moulton vérifie tous les axiomes de Hilbert, y compris les axiomes de congruence de segments, sauf celui (de congruence sur les angles) qui aboutit au théorème de Desargues. Pourtant dans cette géométrie, aucune translation, aucun déplacement ne vient appuyer les axiomes de congruences sur les segments: ces axiomes  ne sont en rien liés au mouvement.

Lire l'article

Revenir au sommaire :

• Les cercles de Tücker

  Par Jacques Bouteloup, professeur de mathématiques à Rouen - L'énoncé E.207 du "Coin des problèmes" de la belle revue mathématique Quadrature (Magazine de mathématiques pures et épicées) numéro 48 (Avril-juin 2003) page 47, avait pour but de montrer que les six projetés orthogonaux des sommets d'un triangle sur ses bissectrices extérieures. La solution proposée dans le numéro 51 (Janvier-Mars 2004) introduisait la notion de cercle de Taylor d'un triangle. Ce cercle est un cas particulier d'une famille générale de cercles attachés à un triangle, les cercles de Tücker, dont cet article donne la définition générale et les principales propriétés.

Cet article est à paraître dans la revue Quadrature, numéro 63 Janvier-Février-Mars 2006 p 28-32. Culture Math remercie l'éditeur EDP qui l'a autorisé à diffuser l'article sur le site CultureMath. Voici, en remerciement, un lien vers le site de Quadrature http://www.edpsciences.org/journal/index.cfm?edpsname=quadrature

Pour les amateurs de joyaux de la géométrie du triangle, signalons quelques sites:

• http://faculty.evansville.edu/ck6/encyclopedia/ETC.html, (Encyclopedia Triangle Center), où on découvrira 3217 points "remarquables" répertoriés.
• http://perso.orange.fr/bernard.gibert/ctc.html, où on découvrira 413 cubiques liées au triangle.

Importer l'article (version pdf, 8 pages)

Pour revenir au sommaire :

 

• Cubiques circulaires passant par leurs foyers singuliers

Par Jacques Bouteloup, professeur de mathématiques à Rouen - Ces courbes possèdent un grand nombre de propriétés remarquables. Souvent appelées "cubiques circulaires focales", elles sont notamment étudiées dans les articles, dans la splendide revue Quadrature (Magazine de mathématiques pures et épicées), de Roux et Tixier (numéro 46 automne 2002 et numéro 47 janvier 2003) sur les configurations de Reye, où elles sont qualifiées d'axées. Dans ces articles comme dans beaucoup d'autres, il n'est pas fait de distinction entre éléments réels ou complexes. L'étude ci-après se place par contre en espace euclidien, supposant donc les éléments introduits (droites, cercles, cubiques) réels. Bien entendu il est nécessaire de supposer cet espace plongé dans son complexifié projectif, ce qui permet d'introduire les points cycliques et de définir les cubiques circulaires comme cubiques les contenant. On appelle, depuis Plücker, foyer d'une courbe un point tel que les isotropes issues de ce point soient tangentes à la courbe. Il est dit singulier si les points de contact sont les points cycliques. Le titre de cette étude est ainsi justifié. Un but fondamental de cette étude est de démontrer l'équivalence de ce passage d'une cubique circulaire par son foyer singulier avec la propriété d'être "auto-isogonale de première espèce", cette notion étant explicitée au début de l'article.

Note de LG Vidiani : comme la cubique étudiée par Monsieur Bouteloup, n'est pas répertoriée dans le catalogue des 413 cubiques liées au triangle (voir le site remarquable de Bernard Gibert http://perso.orange.fr/bernard.gibert/ctc.html), il est naturel de lui donner le nom de son découvreur.

Le beau tracé de cette courbe est dû à Alain Esculier, que nous remercions. Le lecteur pourra se rendre également sur le site http://faculty.evansville.edu/ck6/encyclopedia/ETC.html (Encyclopédie Triangle Center) où il découvrira les propriétés des 3217 points "remarquables" d'un triangle, et rerchercher ceux qui étaient connus au 19ème siècle.

Importer l'article (version pdf, 5 pages)

Pour revenir au sommaire :

 

• Fermeture Hexagonale

  S'inspirant du problème d'Agrégation de Calcul Différentiel et Intégral (Femmes) 1947 cet article donne un critère de fermeture hexagonale et l'illustre dans le cas de faisceaux de cercles à points de base et de Poncelet, ou de solutions d'équations différentielles à variables séparables.
  Le dernier bulletin de l'APMEP n°463 d’avril de mars-avril 2006, montre, sous une forme plus élémentaire, que ces problèmes constituent une mine pour l’enseignement : voir l’article de Jean-Pierre Friedelmeyer « Les problèmes de fermeture : une mine d’exercices à ouvrir en classe », p. 267-276.

Extrait de l’introduction - Les problèmes pouvant donner lieu à des exercices simples, qu’on peut poser en classe, tout en ouvrant à des situations plus élaborées et difficiles sont plutôt rares. Les problèmes de fermeture sont de ceux-là : on peut commencer au collège, continuer au lycée et tomber sur des situations qui paraissent insolubles ou nécessitent des outils très puissants. Souvent, un problème de fermeture facile peut en cacher un autre beaucoup plus difficile : il suffit de modifier légèrement les hypothèses. De sorte que tout un chacun peut, avec un peu d’imagination, inventer ses propres problèmes de fermeture.

Par Lazare Georges Vidiani, Professeur de Mathématiques.

Importer l'article (version pdf, 6 pages)

Pour revenir au sommaire :

 

• Géométrie sur une Strophoïde.

Cet article traite d'une condition d'alignement et de cocyclicité de trois et quatre points sur une cubique circulaire. Son but est de montrer qu’on peut avec des calculs très réduits obtenir de très belles propriétés géométriques, qu’il serait difficille d’obtenir par des arguments géométriques (alignement, cocyclicité, bitangence). Le fait de se limiter à une courbe algébrique de degré 3, une strophoïde, ne réduit pas le principe de la méthode, car on peut démontrer qu’en fait ceci est généralisable, étant une conséquence du théorème intégral d’Abel appliqué aux courbes algébriques.

Utilisation : conditions d'alignement, de cocyclicité.

Par Lazare Georges Vidiani, Professeur de Mathématiques.

Importer l'article (version pdf, 6 pages)

Pour revenir au sommaire :

• Loi de groupe dans un triangle

Une loi de groupe est définie dans un triangle par des conditions de concours et d'alignement. L'auteur montre comment trouver et construire géométriquement l'inverse d'un point, et le composé de deux points, et même les racines carrées d'un point donné.

Utilisation : exemple et illustration géométrique de la théorie des groupes et théorie du calcul barycentrique.

Par Lazare Georges Vidiani, Professeur de Mathématiques.

Importer l'article (version pdf, 14 pages)

Pour revenir au sommaire :

 

• Les épi ou hypo trochoïdes

Photos Vidiani

Cet article propose un classement complet des courbes trochoïdales obtenues par roulement sans glissement. L'auteur donne un tableau à double entrée qui permet suivant les divers paramètres (rayons du cercle de base, de roulement et rapport d'élongation) de donner immédiatement la forme de la courbe. La recherche des développées de ces courbes est une application exploitée. La théorie complète du Centre Instantané de Rotation est donnée en annexe et donne donc aussi une utilisation cinématique à cet article géométrique. Ces problèmes de roulement se retrouvent dans les problèmes d'engrenages. Des simulations animées se trouvent par exemple sur le site de Robert Férréol http://www.mathcurve.com/courbes2d/epitrochoid/epitrochoid.shtml et celui d'Alain Esculier : http://aesculier.chez-alice.fr/ (aller à Rubrique, Maple). En particulier sur http://aesculier.chez-alice.fr/fichiersMaple/wondergraph/wondergraph.html, on verra un jouet "extraordinaire" datant de 1910, le Wondergraph, qui permet de tracer des courbes plus générales que les épi- et hypo-trochoïdes, obtenues elles-mêmes pour certains réglages particuliers (remarque: pour les liens vers les publicités -du Wondergraph- cliquer avec le click droit de la souris et ouvrir, ou bien désactiver votre anti-spam). Par Lazare Georges Vidiani, Professeur de Mathématiques. Importer l'article (version pdf, 15 pages)

Pour revenir au sommaire :

Sur les nombres constructibles

Depuis l'antiquité grecque, l'un des problèmes les plus fameux en mathématiques est de savoir quels sont les figures, et de manière plus générale les nombres que l'on peut construire à la règle et au compas, partant de deux points du plan qui définissent l'unité de longueur. Les réponses à ces questions sont désormais assez complètes, mais il a fallu attendre plus de deux millénaire pour cela.
Nous présentons ici une réponse assez générale au problème posé, donnant des conditions nécessaires et suffisantes de constructibilité. Celles-ci nous permettent au passage de répondre à quelques questions célèbres posées par les grecs. (par Thomas Chomette)

Prérequis :

• Définitions des structures algébriques courantes (anneau, corps, espace vectoriel)
• Arithmétique des polynômes (division euclidienne, relation de Bezout)

Importer l'article en version ps ou pdf.

Pour revenir au sommaire :

• Construction des polygones réguliers

  Parmi les problèmes les plus célèbres en mathématiques, la construction des polygones réguliers à la règle et au compas possède une place de choix puisqu'elle a tenu en haleine les mathématiciens pendant plus de vingt siècles. Il a fallut attendre les travaux du mathématicien allemand Gauss pour que la question soit entièrement résolue.
  Nous introduisons dans ce texte les résultats de Gauss. Le théorème principal démontré en annexe nécessitant quelques connaissances sur les extensions de corps (pour cela, voir par exemple le texte précédent dans lequel nous avons essayé d'introduire certains outils de manière élémentaire), nous nous penchons également sur une méthode plus simple, même si elle ne permet pas d'aboutir au résultat le plus général. (par Thomas Chomette)
  

  Prérequis :

  • Arithmétique des polynômes et des entiers.
  • Relations de trigonométrie.

  Pour la démonstration du théorème de Gauss (en annexe) :

  • Familiarité avec les extensions de corps.
  • Notion de groupe d'automorphismes.
  • Polynômes cyclotomiques.
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• Courbure des surfaces triangulées

  Il existe, en géométrie riemannienne, une notion très importante qui est celle de courbure, mais qui est, hélas, très difficile à définir et à utiliser. On peut cependant, dans le cas des surfaces, en donner une vision assez simple et néanmoins assez précise.
  Dans cet article est définie la courbure en un point comme le "défaut de platitude" de la surface en ce point. C'est une notion qui a une signification locale, liée à une métrique. Elle est utilisée ensuite pour présenter la caractéristique d'Euler-Poincaré des surfaces, et montrer ainsi l'intérêt de la courbure globale.
  Par Frédéric Bosio, université de Poitiers. Article issu du journal de maths des élèves de l'ENS Lyon (JME), Volume 1.
  

  Prérequis :

  • Certains raisonnements demandent un effort de vision dans l'espace.
  
  

  Importer l'article en version pdf.

  Pour revenir au sommaire :

• Problème des 5 cercles

  Si l'on trace les cercles circonscrits aux cinq triangles correspondant aux "branches" d'une étoile à cinq branches, on s'aperçoit que les points d'intersection de chacun de ces cercles avec le suivant sont cocycliques !
  Ce problème de géométrie assez classique à été remis au goût du jour par le président chinois, à l'occasion du congrès international des mathématiciens (Pékin, août 2002)...
  Par Thomas Chomette, sur une suggestion de Charles Torossian, ENS/CNRS.
  

  Prérequis :

  • Nombres complexes, affixe d'un point du plan.
  • Angles et argument d'un nombre complexe.
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• Tas d'oranges, cristaux et empilement de sphères

  Comment empiler efficacement des oranges (ou tout autre fruit sphérique) de façon à obtenir un tas occupant aussi peu de volume que possible ? Est-il préférable d'empiler des couches où les fruits sont disposés en carrés, ou une disposition en triangles est-elle plus efficace ? Ce problème, en apparence anodin, mais dont le champ d'application s'étend de l'étude des cristaux à la théorie des codages informatiques, aura donné du mal aux mathématiciens pendant près de quatre siècles : dès 1610, Kepler formulait une conjecture sur la question, mais il aura fallu attendre 1998 pour que les travaux de Thomas Hales en apportent la preuve de façon rigoureuse. (Par Denis Auroux, CNRS/École Polytechnique)
  
  

  Prérequis :

  • Calculs élémentaires d'aires et de volumes.
  • Un peu de vision dans l'espace.
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• Reconnaître effectivement les Ensembles Algébriques Réels

  La question est de savoir s'il existe une méthode qui, étant donné un objet géométrique W, permet de savoir si W peut être décrit par des équations algébriques, à des changements qui ne modifient pas sa topologie près. Ce problème fait intervenir de manière fondamentale la notion de triangulation, et plus généralement mène à l'introduction de quelques notions importantes de topologie qui peuvent souvent se comprendre à l'aide de dessins. Dans le cas de la dimension 1 ou 2, les conditions se révèlent relativement simples.
  Dans la dernière partie de ce texte, d'un abord plus ardu, on donne une idée d'outils plus sophistiqués qui permettent de présenter une méthode de décision en dimension 3, et de montrer que le problème est en pratique indécidable en dimension plus grande. (par Michel Coste, CNRS/Université de Rennes 1)
  
  

  Prérequis :

  • Notion de surface, d'équation d'une surface
  • Homéomorphisme, transformations de l'espace telle l'inversion...
  • Pour la dernière partie : bonne vision dans l'espace (intersections de surfaces).
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• Pour nouer, il faut courber

  Quand on découvre les mathématiques, on étudie des formes et des nombres. Une manière usuelle d'associer des nombres à une forme est de mesurer des longueurs. Ce texte nous présente de façon intuitive les notions de courbure et de torsion des courbes et des surfaces, et présente un théorème classique sur la courbure des nœuds.
  Il peut constituer une introduction à la Courbure des surfaces triangulées, ou au texte sur Gaspard Monge. Le style adopté par l'auteur est très simple et illustré par de nombreux dessins. Quelques annotations mathématiques viennent donner une idée des outils nécessaires pour aller plus loin. (par Patrick Popescu-Pampu, Maître de Conférences, Universté Paris 7)
  

  Prérequis :

  • Aucun pour l'essentiel du texte, les annotations mathématiques se basent sur le niveau lycée (dérivation, intégration).
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• Autour des triangles inscrits sur une hyperbole équilatère

  Ce texte a une forme inhabituelle sur ce site : c'est un problème destiné à explorer certaines propriétés de l'hyperbole y = 1/x. Il mélange géométrie plane, géométrie analytique et utilisation des moyens de calcul modernes, et pourra donner des idées d'exercices aux profeseurs... tout en leur pemettant de s'exercer !

  Une solution détaillée est fournie, ainsi que des figures interactives réalisées en CabriJAVA permettant d'illustrer les notions évoquées ainsi que certaines notions connexes.

  Ce texte a été conçu dans le cadre du groupe de Calcul Formel de l'IREM de Lille (par Géry Huvent, Michel Gouy et Alain Ladureau).
  
  

  Prérequis :

  • Géométrie plane élémentaire, géométrie analytique. Certaines questions ont trait à l'utilisation de logiciels de calculs, comme Maple ou les calculatrices modernes (la TI 92 est l'exemple utilisé dans les solutions).
  
  

  Importer l'article en version ps ou pdf. Voir les figures.

  Pour revenir au sommaire :

• Gaspard Monge, de la planche à dessin aux lignes de courbure

  L'expérience du dessin de plans et la curiosité scientifique de Gaspard Monge ont à notre avis influencé sa manière, très visuelle, de raisonner en mathématiques. Il était aussi un enseignant remarquable. Le souci de former les futurs cadres de la nation, donc d'expliquer à la fois les notions mathématiques et leurs éventuelles applications est sans doute lié à son besoin de voir et de représenter de manière précise les objets mathématiques qu'il définit.

  Par Rémi Langevin, Professeur à l'Université de Dijon. Ce texte est extrait du recueil "De la Méthode", publié aux Presses Universitaires Franc-Comtoises sous la direction de Michel Serfati.
  
  

  Prérequis :

  • Une vision dans l'espace raisonnable. Pour une initiation à la notion de courbure, on pourra se référer au texte Pour nouer, il faut courber.
  • Le paragraphe 4.1 utilise des dérivées partielles (mais ce n'est pas nécessaire pour la lecture de la suite du texte !).
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• Principe de Fermat, applications à la réflexion et à la réfraction

  Le principe de Femat s'énonce de manière simple : Pour aller d'un point-source S à un point-détecteur D après une réflexion ou une réfraction, la lumière suit un chemin pour lequel le temps de parcours est extrêmal (i.e. minimal ou maximal). A partir de ce principe, ce texte démontre les lois classiques de la réflexion et de la réfraction (en particulier la Loi de Descartes).

  Par Jean Gounon, professeur de mathématiques.

  Prérequis :

  • Niveau Première scientifique (avec une bonne maîtrise des dérivées).
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• Arc en ciel, soucoupes volantes, toupies, courbes elliptiques, et tout ça

  Ce texte nous donne quelques exemples de singularités lagrangiennes. Mais ne vous effrayez pas tout de suite ! L'auteur prend le parti de ne jamais définir cette notion, préférant tourner autour en prenant plusieurs points de vue amusants (ceux qui donnent son titre à l'exposé) pour insuffler l'intuition de ce qu'elles sont.

  Nous y voyons par exemple comment mettre une structure de groupe sur une courbe elliptique, entre autres tours de magie géométrique.

  C'est aussi l'occasion de réflexions personnelles de l'auteur sur "ce que devrait être" un bon texte de vulgarisation mathématique, dans un style direct, explosif et divertissant.

  Un peu plus tard, nous donnerons un versant "théorisé" avec définitions, propriétés, etc... à cette notion.

  Par Michèle Audin, Professeure à l'Université Louis Pasteur de Strabourg.

  Prérequis :

  • Aucun !
  
  

  Importer l'article en version pdf.

  Pour revenir au sommaire :

• La théorie mathématique des Nœuds

  Toute personne se trouvant aux prises avec un embrouillaminis de fils est amenée à se demander si les fils sont simplement emmêlés, ou si des nœuds viennent corser l'affaire et rendre le démélage plus compliqué. Auquel cas, se pose la question de la marche à suivre pour dénouer la pelote, ou au moins d'éviter d'aggraver la situation !

  La théorie des nœuds est l'abstraction naturelle de cette interrogation, et le texte que nous vous proposons cette semaine en survole les bases, expliquant ce qu'est un nœud pour un mathématicien, et comment exprimer en termes rigoureux la questions « est-ce qu'il est vraiment noué ou pas ? »

  Par Jérôme Dubois, chercheur à l'Université de Genève.
  Ce texte a été écrit par l'auteur pour présenter ses travaux de thèse, à l'occasion de sa participation au Prix Jeune Chercheur 2004 de la ville de Clermont-Ferrand, dont il a reçu un accessit.
  

  Prérequis :

  • Aucun pour l'essentiel du texte, qui s'adresse au grand public.
  • Certains paragraphes parlent de la notion de groupe (on pourra en profiter pour regarder notre introduction à ce domaine.)
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• La médiatrice (en BD)

  Ce texte est une petite Bande Dessinée expliquant avec humour ce qu'est la médiatrice d'un segment, à un niveau collège, et est un extrait du travail de l'auteur, qui souhaiterait trouver un éditeur.

  N'hésitez pas à lui écrire si vous êtes intéressé par son travail !

  Par Jean-Pierre Guidoni, professeur au collège-lycée Pascal Paoli, à Corte.

  Prérequis :

  • Aucun !

Importer l'article en version pdf.

Pour revenir au sommaire :

Analyse

Les mathématiques du mouvement : Introduction informelle aux systèmes dynamiques

Revenir au sommaire :

Equations fonctionnelles

Les équations fonctionnelles, par leur diversité, le fait qu'il n'y ait pas de méthode standard ou universelle pour les résoudre, rivalisent aussi bien avec l'arithmétique que la géométrie, pour montrer la richesse des mathématiques. Elles obligent aussi l'étudiant ou le chercheur à appréhender la nécessité d'une argumentation rigoureuse. L'extrême variété des domaines où on les rencontre (recherche, problèmes de concours, exercices d'oraux, sujets de compétitions internationales telles que les O.I.M....) ne fait que renforcer leur attrait, d'autant plus que chaque jour amène de nouveaux exemples originaux (sites web, revues, sujets de concours, ou de compétitions,...). L'article qui suit a pour but d'essayer de dégager 6 méthodes principales qui permettent de résoudre quatre vingt dix neuf pour cent des exemples proposés au niveau Classes Préparatoires Scientifiques.

Les cinq premières pages (sur 14) de cet article ont été publiées dans la revue Quadrature (Magazine de mathématiques pures et épicées http://www.edpsciences.org/journal/index.cfm?edpsname=quadrature) de Juillet-Septembre 2004, numéro 53 pages 7-12; elle sont reproduites, avec l'aimable autorisation du rédacteur en chef Olivier Courcelle, que nous remercions.

Les neuf pages suivantes sont un catalogue d'exemples (trente cinq) très divers, avec leur référence précise et l'indication de leur solution. Pour garder une dimension raisonnable à l'article publié dans Quadrature, elles n'avaient pas été publiées, mais la dernière note de l'article précisait que les lecteurs intéressés, pouvaient demander leur envoi, ce que beaucoup ont fait à l'époque. Les voici rendues accessibles au plus grand nombre. Pour d'autres pistes et d'autres références bibliographiques les lecteurs peuvent se reporter à l'article « Racine carrée fonctionnelle » du même auteur, sur le site de CultureMath.

Importer l'article (version pdf, 14 pages)

Par Lazare Georges Vidiani, Professeur de Mathématiques

Revenir au sommaire :

Jauge d'une cuve à Mazout

Il s'agit d'étalonner une jauge de cuve à Mazout cylindrique bombée, horizontale, et d'utiliser du calcul intégral pour établir la formule exacte de cette jauge.

Importer l'article (version pdf) et la figure correspondante

Par Lazare Georges Vidiani, Professeur de Mathématiques

Revenir au sommaire :

• Les motifs des pelages d’animaux

Les motifs de pelages d'animaux sont expliqués suivant la théorie de réaction-diffusion due à Turing (qui a contribué à casser les codes secrets de la machine Enigma). Qui croirait que ceci est en fait une illustration de la théorie des équations aux dérivées partielles et d'un problème de conditions aux limites? Ces modélisations servent aussi pour gérer la lutte contre les feux de forêts.   Cet article est modélisé par de très belles illustrations sur le site d'Alain Esculier et d'Yann Bouret de l'ENS de Chimie UMR 8640 (lab P9) qui les a conçues à la demande de l’auteur.

Utilisation : équations au dérivées partielles et chimie, équation de réaction-diffusion.

Importer l'article (version pdf, 7 pages) .

Par Lazare Georges Vidiani, Professeur de Mathématiques.

Voici quelques illustrations animées des modèles présentés dans l'article. Les visiteurs intéressés peuvent en demander d'autres à l'auteur.

panthère animation

zèbre

panthère rose animation

arc-en-ciel animation 1 animation 2

 

Revenir au sommaire :

• Le produit d'Hadamard de deux séries entières

Quel lien y a t-il entre le rayon des séries entières et celui de leur produit d'Hadamard? L'auteur donne à la façon de Cyrano dans la tirade des nez de multiples applications et illustrations dont une formule donnant la somme du produit d'Hadamard en fonction de celles des deux séries arguments.   Utilisation : variation originale sur les séries entières.

Par Lazare Georges Vidiani, Professeur de Mathématiques.

Importer l'article (version pdf, 4 pages) .

Revenir au sommaire :

Critères d'Ermakov

Résumé: En 1870 Vassili Petrovitch Ermakov découvre des critères très fins de convergence de séries et d'intégrales ; ces critères se retrouvent (de manière anonyme) dans beaucoup d'exercices d'oraux. L'auteur en rappelle l'énoncé en illustrant leur principe.  
Erratum: dans le dernier théorème encadré page 2, la suite p_n doit être non bornée.
Utilisation: convergence des séries numériques.

Par Lazare Georges Vidiani, Professeur de Mathématiques.

Importer l'article (version pdf, 3 pages) .

Revenir au sommaire :

• Racine carrée fonctionnelle

Inspiré du problème d'agrégation 1949 proposant de rechercher les fonctions g inconnues telles que g(g(x))=f(x) (f donnée), cet article, abondamment illustré par des exemples concrets, montre comment trouver les solutions et donne diverses applications très récentes de cette théorie (réseaux de neuronnes (et le fameux Perceptron), géographie pour la prédiction de l'occupation des sols, recherche des périodes en théorie du chaos, prédiction boursière, technique du laminage en industrie,...). Dans l'enseignement, il montre que des problèmes abstraits peuvent avoir de nombreuses applications pratiques.
Par Lazare Georges Vidiani, Professeur de Mathématiques.

Erratum (12 02 09 14h30) : 8 lignes de texte avant la fin de la page 1, remplacer (x/2)^n=(y/2)^m par x/2^n=y/2^m.

Importer l'article (version pdf, 8 pages) .

Revenir au sommaire :

 

• Le théorème de JUEL et la surface de CLEBSCH

Recherche des 27 droites sur une surface cubique non réglée, représentation paramétrique, double six de Schlaffli, lien avec la théorie des groupes et même lien avec la théorie des super-cordes. L'auteur, dans un style très personnel, ne cache rien de toutes les étapes de sa recherche, et des problèmes divers soulevés et fournit même une photo du bijou offert à Juel le 25 janvier 1925, pour son jubilé scientifique.
Par Lazare Georges Vidiani, Professeur de Mathématiques.

Utilisation dans l'enseignement : pour les classes préparatoires aux grandes écoles, en relation avec la théorie des surfaces et en illustration du groupe Psp4(F2).

Lire l'article

Revenir au sommaire :

• Le théorème de Sharkovskii

  Ce résultat est assez connu sous une forme plus faible : période 3 implique période n pour tout entier n. C'est-à-dire qu'une fonction continue, d'un segment dans lui-même, ayant un point de période 3 a nécessairement un point de période n pour tout n.
  En fait, ceci est une conséquence du théorème de Sharkovskii, qui affirme que si une fonction continue d'un segment dans lui-même a un point de période m (m entier), alors cette fonction a un point de période n pour tout n plus grand que m pour l'ordre de Sharkovskii (ordre sur les entier dont 3 est bien sûr le plus petit élément).
  Par Jean-Yves Briend, université de Provence. Article issu du journal de maths des élèves de l'ENS Lyon (JME), Volume 1.
  

  Prérequis :

  • Analyse réelle : théorème des valeurs intermédiaires...
  • Topologie élémentaire : intersections de compacts emboîtés, image réciproque de segments...
  
  

  Importer l'article en version pdf.

  Pour revenir au sommaire :

• Propagation d'épidémie

  La théorie des épidémies fournit de nombreux systèmes d'équations différentielles ou aux dérivées partielles. On a d'autre part une idée intuitive du comportement de ces phénomènes, de la propagation de ces maladies. Y interviennent des phénomènes de contamination, de diffusion... Nous allons ici prendre l'exemple de la diffusion de la rage dans une population de renards, et en présenter quelques modèles assez simples.
  Ceux-ci sont accompagnés de simulations numériques. Les programmes utilisés sont disponibles, commentés, en version matlab et scilab (scilab est un logiciel libre distribué par l'INRIA, que l'on peut télé-charger ici).
  Par Thomas Chomette, avec l'aide d'Emmanuel Grenier, ENS Lyon.
  

  Article disponible en version html, ps ou pdf.

  Pour revenir au sommaire :

• Petits pièges de la simulation numérique

  La simulation numérique ne pose pas toujours seulement des problèmes de capacités de calcul : même avec des ordinateurs de plus en plus puissants, l'opération laisse encore des problèmes au mathématicien ! Il s'agit en effet de mettre en place des algorithmes qui fonctionnent, or même dans des cas très simples, on ne peut pas faire n'importe quoi.

  Texte accompagné de simulations numériques en java. Les algorithmes sont également déclinés et mis à disposition en version matlab et scilab (scilab est un logiciel libre distribué par l'INRIA, que l'on peut télé-charger ici).
  Par Emmanuel Grenier, ENS Lyon. Illustrations de Thomas Chomette.
  

  Prérequis :

  • Éléments de calcul différentiel (fonction de deux variables, dérivée partielle).
  
  

  L'article seul, en version ps ou pdf. Illustrations numériques, disponibles en version html.

  Pour revenir au sommaire :

• Arbres et dérivée d'une fonction composée

  On connaît des formules de dérivation à un ordre quelconque pour un produit de fonction (formule de Leibnitz). Pour ce qui est d'une somme de fonctions, c'est encore plus évident : la dérivée n-ième de la somme est la somme des dérivées n-ièmes, par linéarité.
  En revanche, pour ce qui est de la composée de deux fonctions, on ne sais pas faire... Nous allons voir ici que le problème se transpose en quelque chose de purement combinatoire sur les arbres. Une illustration de plus des ponts surprenants qui peuvent se créer entre des domaines a priori complètement étrangers l'un à l'autre, ici l'analyse classique et la théorie des graphes !
  Par Thomas Chomette, sur une suggestion de Charles Torossian, ENS/CNRS. Pour aller (beaucoup) plus loin dans le domaine, un article intitulé "Runge-Kutta methods and renormalization", par Christian Brouder, est disponible ici.
  

  Prérequis :

  • Notion d'arbre (graphe sans cycle).
  • Règles de dérivation usuelles.

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• Homographies et suites récurrentes

  On apprend à tous les étudiants en mathématiques comment étudier une suite récurrente définie par une homographie : on cherche les points fixes de l'homographie, puis on définit une autre suite à l'aide de la première, en distinguant le cas où l'homographie a un point fixe double, et cette suite se révèle miraculeusement être une suite géométrique ou arithmétique...
  Partant de cette méthode, on on s'aperçoit qu'en rajoutant au plan complexe un "point à l'infini", les choses s'expliquent de manière plus simple, plus élégantes, plus convaincantes. En réalité, nous avons introduit rien moins que la droite projective complexe, un des cas le plus simples de la géométrie projective, mais qui permet d'introduire de nombreuses notions fondamentales. (par Thomas Chomette, avec l'aide de Gaëtan Chenevier, ENS)
  

  Prérequis :

  • Suites récurrentes.
  • Composée de fonctions, bijection réciproque.
  • Calcul matriciel en dimension 2, changement de base.
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• L'intégration selon Riemann et selon Lebesgue

  Ce texte est une présentation systématique de deux théories de l'intégration : celle de Riemann et celle de Lebesgue. Ces deux cadres sont décrits par le menu, ainsi que les résultats les plus marquants (le plus souvent sans démonstration). L'objectif de ce texte est de servir de référence rapide pour la lecture d'autres textes, ou pour avoir une idée d'ensemble de ces théories sans devoir se plonger dans les détails les plus techniques, ou acquérir au prélable trop de connaissances abstraites.

  Par Jean Gounon.

  Prérequis :

  • Une connaissance raisonnable du langage des intégrales (niveau terminale), et une habitude des notations condensées (quantificateurs etc...) est utile.
  
  

  Importer l'article, en version ps ou pdf.

  Pour revenir au sommaire :

• Signal numérique et théorie de l'échantillonnage

  Du compact-disc, au DVD, en passant par l'appareil photo numérique, le scanner, et une hypothétique télévision numérique (plus en panne politique que technologique), le numérique a fait une entrée progressive mais écrasante et sans doute irréversible dans la vie quotidienne. Ce n'est évidemment pas sans raison : pour le meilleur et pour le pire, les signaux numériques sont plus simple à dupliquer (et donc à diffuser), ils peuvent être efficacement compressés et transmis, ils sont faciles à stocker, et on peut aisément les manipuler.

  De plus, les vendeurs n'ont de cesse de vanter les qualités des signaux numériques, tant audio que vidéo. Dans cet article, nous limiterons quelque peu cet enthousiasme et verrons qu'un signal numérique construit sans précaution peut présenter des défauts perceptuels flagrants. Fort heureusement, un examen quelque peu minutieux de la nature des signaux numériques et un passage par l'analyse de Fourier nous montrerons comment aisément éviter ces défauts.

  Par Frédéric Cao, Chargé de recherches IRISA/INRIA.

  Prérequis :

  • Une certaine familiarité avec la notion d'intégrale est nécessaire. Certains passages impliquent d'avoir déjà vu des espaces de fonctions (convergences de suites et séries de fonctions...) mais ne sont pas obligatoires pour la lecture générale de l'article.
  
  

  Importer l'article, en version ps ou pdf.

  Pour revenir au sommaire :

• Les intégrales de Coxeter

  En 1926, H.S.M. Coxeter calcula certaines intégrales intervenant dans des calculs de volumes, lors de ses études du groupe cristallographique. Pour ce faire, il utilisa des méthodes géométriques avancées, et soumit la découverte d'une preuve "élémentaire" à la sagacité des lecteurs de la Mathematical Gazette. Seul le mathématicien Hardy trouva une réponse !

  Cet article se propose donc de calculer ces intégrales récalcitrantes (qui interviennent dans plusieurs champs de la géométrie) en n'utilisant pas de méthodes excédant le niveau Licence. Par ailleurs, l'auteur utilise un style très personnel rendant vivantes ses pérégrinations au milieu des concepts abstraits foisonnant autour de ces intégrales, et replace les idées dans leur contexte afin de ne pas noyer le lecteur dans la technique.

  Par Lazare Georges Vidiani, Professeur de Mathématiques, cet article est paru dans le numéro 50 de la revue Quadrature que nous remercions vivement (en particulier Olivier Courcelle qui nous a donné l'accord de publication en quelques heures !).

  Prérequis :

  • Une bonne habitude des calculs d'intégrales est fortement conseillée.
  • Cet article traitant d'un sujet frontalier avec plusieurs domaines, une certaine culture mathématique (groupe cristallographique, par exemple) aidera à comprendre certains passages - qui ne sont pas nécessaire pour lire le corps du texte.
  
  

  Importer l'article, en version ps ou pdf (15 pages).

  Pour revenir au sommaire :

• Equirépartition d'une suite de nombres

  Ce texte part d'une observation expérimentale: quand on calcule une trentaine ou plus de valeurs de 2^n , on constate que le premier chiffre est nettement plus souvent "1" que n'importe quel autre. Il arrive dans plus de 30% des cas ! Mais que signifie ce pourcentge ?

  Cette observation contre-intuitive amène à se poser la question des probabilités sur l'ensemble des entiers naturels, et rectifier l'intuition, trompeuse, puis définir la notion d'équirépartition d'une suite de nombre dans [0;1], c'est à dire à définir rigoureusement l'idée qu'une suite peut "tapisser" uniformément [0;1].

  Développant cette petite théorie, on arrivera à lever ce paradoxe apparent.

  Par Thomas Chomette, professeur en classes préparatoires, et Farouk Boucekkine, ENS, d'après un texte de François Fayard, professeur en classes préparatoires.

  Prérequis :

  • Une bonne habitude de la manipulation des suites et de leurs limites pour comprendre l'essentiel.
  • Quelques notions sur la topologie de R (densité) sont utiles (mais rappelées en cas de nécessité.)
  • Pour lire certaines démonstrations, la définition de l'intégrale de Riemann, et quelques résultats classiques sur les suites de fonctions (Stone-Weierstrass). (ce n'est pas nécessaire pour lire les énoncés, exprimés de la manière la plus simple possible.)
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• Le lemme de Baire

  Ce texte nous présente le lemme de Baire, ainsi que son créateur, René Baire, mathématicien maudit du début du XX° siècle. Il nous raconte, comme un récit, certaines théories qui ont révolutionné l'analyse il y a une centaine d'années, en les entremêlant d'éléments biographiques sur les principaux acteurs de ces petites révolutions, Borel, Lebesgue et Baire, moins connu du fait de son histoire plus tragique. Nous y croiserons, pêle-mêle, rivalité entre chercheurs, fonctions pathologiques (continues mais pas dérivables, etc...), remarques générales et petites digressions pour connaisseurs.

  L'analyse, de nos jours, nécessite un arsenal de notations qui effaye facilement les lecteurs, et il est bon de se (re)plonger dans ces notions, modernes par leur contenu (toujours enseigné dans l'enseignement supérieur) mais qui ont été crées à une époque où l'on écrivait encore les mathématiques presque sans symboles...

  Par ailleurs, ce texte sera une source d'inspiration et une illustration très intéressante pour ceux qui souhaitent passer l'agrégation de mathématiques, le lemme de Baire et ses applications en étant de grands classiques.

  Il se termine sur quelques réflexions d'ordre pédagogique à propos des difficultés qu'on peut rencontrer dans la vulgarisation des mathématiques.

  Nous remercions à cette occasion Paul-Louis Hennequin et Animath pour nous avoir autorisé à utiliser ce texte (et celui de Michèle Audin au paravant.)

  Par Gilles Godefroy, Directeur de Recherches CNRS/Paris

  Prérequis :

  • Notions essentielles sur les fonctions (dérivations, continuité) pour l'essentiel du texte.
  • Théorie des ensembles pour certains passages
  • la démonstration du théorème nécessite une habitude des notations et notions de la topologie (niveau Licence ou Maîtrise.)
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• 
  

• Addendum sur l'équirépartition

  Ce petit addendum de deux pages démontre un résultat simple mais surprenant : si l'on prend n chiffres quelconques, il existe une infinité de puissances de 2 commençant par ces chiffres !

  Par François Lo Jacomo, informaticien, trésorier d'Animath.

  Prérequis :

  • Notre texte Equirépartition d'une suite de nombres.
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

 
 

Théorie des jeux :

• Le Berlekamp's switching game

  Le ``Berlekamp's switching game'' est un jeu inventé par Elwin R. Berlekamp et David Gale. Son support est un tableau carré de m*m ampoules, contrôlées par 2m interrupteurs frontaux, un pour chaque ligne ou colonne. Quand un interrupteur est basculé, les ampoules qui étaient allumées dans la ligne ou la colonne correspondante sont éteintes, et celles qui étaient éteintes sont allumées. Le jeu consiste à trouver, pour un état initial donné, le nombre minimal d'ampoules allumées après manipulation à volonté des interrupteurs commandant les lignes et les colonnes, puis à maximiser ce nombre par un choix judicieux de l'état initial.
  Par Jonathan Le Roux, ENS. Texte adapté d'un travail réalisé dans le cadre des TIPE, sous la direction de Philippe Esperet, professeur de Maths Spé MP* au lycée Henri IV, Paris Vè.
  

  Prérequis :

  • Notions d'algèbre linéaire (dimension d'un sous espace, produit matriciel, opérations sur les lignes et les colonnes d'une matrice).
  • Corps finis (surtout le corps à deux éléments).

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• Jeux sur les graphes et théorème de Ramsey

  Si l'on prends six personnes au hasard, alors trois d'entre elles se connaissent, ou alors on peut en trouver trois dont aucune ne se connaissent. Cette remarque, en apparence anodine, permet de déboucher sur toute une théorie combinatoire. En effet, reformulée en termes de graphe, cela signifie que, si l'on colorie les arêtes du graphe complet à six sommet en deux couleurs, alors on peut trouver un triangle dont les trois arêtes sont de la même couleur. La question se pose alors pour d'autres type de configurations, et l'on verra que le résultat reste valable à condition de colorier les arêtes d'un graphe suffisamment gros. (par Thomas Chomette)
  

  Prérequis :

  • Principes combinatoires élémentaires (principe des tiroirs, etc)
  • Récurrence doubles.
  • Familiarité avec les graphes simples.

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• Jeux et stratégies

  Comment gagner à coup sûr au jeu de Nim ? Peut-on gagner à coup sûr aux échecs ? Ou bien est-ce qu'au contraire deux ordinateurs infiniment puissants jouant l'un contre l'autre aboutiraient nécessairement à une partie nulle ?
  Toutes ces questions tournent autour de la notion de stratégie, le jeu de Nim comme le jeu d'échecs étant des jeux à deux joueurs, finis. Après avoir montré que l'étude de tous ces jeux peut se ramener à des propriétés de certains arbres, nous définissons ici la notion mathématique de stratégie. L'intérêt étant que, notamment, ce formalisme nous permet de savoir que va être l'issue de la partie, si les deux joueurs jouent parfaitement. (par Thomas Chomette)
  

  Prérequis :

  • Notion d'arbre (graphe sans cycle).
  • Notion intuitive de stratégie.
  • (Décomposition en base 2.)

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

Algèbre :

Le Rubik's cube, Groupe de poche

Par Pierre Colmez (École Polytechnique - CNRS)

Résumé- Ce petit texte vise à expliquer pourquoi, si on démonte le cube de Rubik et qu'on le remonte au hasard, on a une chance sur douze de pouvoir le résoudre.  La démonstration est un joli exercice de théorie des groupes utilisant, en particulier, la notion d'action de groupe opérant sur un ensemble.

Utilisation  en classe- Cet article illustre de façon originale la notion d’action de groupe opérant sur un ensemble. Le lecteur qui n’aurait pas manipulé cette notion depuis un certain temps  pourra trouver  les prérequis nécessaires sur CultureMATH  dans l'article Intoduction à la théorie des groupes de Farouk Boucekkine et Thomas Chomette.
Ce texte n’est pas utilisable dans l’enseignement  secondaire  ;en revanche, les enseignants du supérieur trouveront dans cet article une façon originale pour aider leurs étudiants à maîtriser le vocabulaire d'action de groupes.  

Lire l'article

Pour revenir au sommaire :

La transformation du Boulanger

Un petit film de P. Trivic (la Tempête) dans le cadre du "quart-d'heure mathématique" sur les systèmes mélangeants, commenté par le savant géométre Marcel Berger, diffusé sur la 7 le 24 novembre 1990 à 22h30, présentait une séquence particulièrement percutante : Le portrait de Poincaré -initiateur de la théorie du Chaos- était déstructuré par une transformation dite de la pâte feuilletée (on étale la pâte intialement en carré, et on replace les morceaux débordants pour reconstituer le carré). Puis –oh miracle- au bout de 241 opérations dé-structurantes, le portrait de Poincaré réapparaissait "intact". Un bon dessin valant mieux qu'un long discours, observez l'image ci-contre, ou bien allez voir ici. Le but de cet article est d'expliquer ce qui se passe, en utilisant algèbre linéaire (matrice) et arithmétique (mise en évidence de la période), en l'illustrant sur une image de papillon déstructuré puis ressuscité. On peut observer le phénomène ici. Par Lazare Georges Vidiani, Professeur de Mathématiques. Importer l'article en version pdf (8 pages, 2 Mo)

Pour revenir au sommaire :

 

Loi de groupe sur une surface.

 

Le lecteur est habitué aux lois de groupe usuelles dans des ensembles algébriques, parfois géométriques plans sur une hyperbole ou une cubique (en liaison avec les critères d’alignement de trois points, succédané des conséquences du théorème d’Abel, et utilisé maintenant en codage elliptique). Voici un exemple de loi de groupe sur une surface. Cette loi a été proposée dans un problème de concours à l’école supérieure des Industries chimiques de Nancy en 1947, dont l’énoncé est partiellement reproduit dans les « Exercices de Géométrie » de E. Râmis. Ce sujet fait partie d’une dizaine de problèmes très originaux pour l’époque dont l’auteur était Jean Frédéric Auguste Delsatre, qui était alors le Doyen de la Faculté des Sciences de Nancy. Son thème est le point de départ périodiquement de nombreuses questions d’oral des concours.

Utilisation : montrer que la théorie des groupes a des illustrations géométriques et ne se réduit pas à des manipulations algébriques.  

Par Lazare Georges Vidiani, Professeur de Mathématiques.

Importer l'article en version pdf (3 pages)

Pour revenir au sommaire :

• Équations algébriques

  Une équation n'est rien d'autre qu'une égalité entre deux membres. Souvent, il s'agit de déterminer une certaine quantité, connaissant simplement une égalité qui fait intervenir cette quantité inconnue. On parle d'équation algébrique lorsque l'on cherche à déterminer les racines d'un polynôme. Nous allons ici nous intéresser plus spécifiquement à ce type d'équation, et voir notamment des méthodes générales pour résoudre les équations algébriques de degré allant de 1 à 4. (d'après un article de Xavier Caruso, ENS, et un historique issu du forum fr.sci.maths, dont on peut trouver une compilation sur le site faq.maths)
  

  Prérequis :

  • Manipulation d'expressions polynomiales.
  • Nombres complexes.
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

  Une remarque sur la méthode de Cardan et ses limites, d'après Hugues Randriambololona, ENST (nécessite quelque connaissances générales sur les extensions de corps). Version ps ou pdf.
   

• Intégration de polynômes, points de Gauss

  Peut-on calculer l'intégrale d'une fonction (sur l'intervalle [0,1] par exemple) si l'on ne connaît que sa valeur en 3 points ? Évidemment non, sauf si l'on sait en outre qu'il s'agit d'un polynôme de degré 2 ! Facile, me direz vous : dans ce cas, la donné des valeurs en trois points, quels qu'il soient, permet de retrouver le polynôme et donc de calculer cette intégrale. Beaucoup plus fort : si l'on choisit correctement ces trois points, on peut calculer l'intégrale de n'importe quel polynôme de degré 5, en ne connaissant que sa valeur en nos trois points. Et cette fois, plus question de trouver le polynôme... (par Thomas Chomette, sur une suggestion de Charles Torossian, ENS/CNRS.)
  

  Prérequis :

  • Définition d'un espace vectoriel, d'une application linéaire.
  • Une certaine familiarité avec la notion de produit scalaire peut être utile.
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• Les tonalités musicales vues par un mathématicien

  L'objet de cet article est, en particulier, de montrer que le choix des 7 notes de la gamme classique (do-ré-mi-fa-sol-la-si) parmi les 12 notes du système tempéré (do-do#- ré-ré#-mi-fa-fa#-sol-sol#-la-la#-si) est le seul choix possible qui satisfasse à des critères naturels liés à la transposition. L'approche utilisée, qui n'emploie que des considérations mathématiques élémentaires, fournit également des justifications purement mathématiques ou combinatoires à l'usage de la gamme mineure augmentée (la-si-do-ré-mi-fa-sol#) ou d'autres gammes utilisées dans l'histoire (telle la gamme pentatonique javanaise), ou encore à l'importance d'autres gammes et accords classiques de l'harmonie musicale.

  Par Michel Broué, Professeur de l'Université Paris Diderot

  Cet article a été publié dans "Le temps des savoirs", Revue de l'Institut Universitaire de France, 4 , D.Rousseau & M.Morvan eds., Odile Jacob, Paris (2002), pp. 37-78. Nous remercions vivement son auteur pour son amabilité.

  Prérequis :

  • Aucun.
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• Introduction à la Théorie des Groupes

  Ce texte en deux parties a pour but d'introduire les lecteurs à cette avancée majeure du dix-neuvième siècle qu'est la notion de groupe.

  Il a été écrit afin de servir d'appoint aux candidats à l'agrégation interne ou externe, mais aussi pour toute personne désireuse de se cultiver !

  Première Partie :

  La notion de groupe et ses applications les plus classiques est présentée ici avec deux objectifs. Premièrement, donner une base solide permettant de lire des textes utilisant cette notion (comme Les colliers de Polya. Deuxièmement, essayer de faire sentir les idées générales qui sous-tendent les définitions et résultats présentés, que l'on retrouvera dans l'étude d'autres structures algébriques.

  Comme le texte est long, une version courte est disponible pour ceux qui n'auraient besoin que d'une référence rapide.

  Deuxième Partie :

  Cette Deuxième Partie, plus courte, a pour but d'ouvrir les notions présentées auparavant vers les travaux les plus modernes d'une part, et les applications importantes de la théorie d'autre part.

  Ainsi, on entre ici dans des considérations plus techniques: quelques exemples plus développés, la notion de sous-groupe distingué, souvent mal comprise, décortiquée... Mais on survole également sans entrer dans les détails des applications historiques ou des développements modernes.

  N'hésitez pas à nous demander de développer certains points survolés ici !

  Par Farouk Boucekkine (avec l'aide de Thomas Chomette), ENS.

  Prérequis :

  • Aucun pour la majorité de la Première Partie. Certains exemples présupposent quelques connaissances générales, de niveau terminale scientifique au maximum (définition des nombres complexes par exemple).
  • La Deuxième Partie requiert la connaissance du contenu de la première.
  
  

  Importer la Première Partie entière au format ps ou pdf.
  Importer sa version courte au format ps ou pdf.
  Importer la Deuxième Partie au format ps ou pdf.	Pour revenir au sommaire :

• Des chapeaux, des couleurs et des structures algébriques

  Imaginez une ronde de 100 personnes, portant tous des chapeaux de deux couleurs différentes. Chacun connait la couleur du chapeau de tous les autres, mais pas celle du sien. Maintenant, chacun son tour, les joyeux lurons peuvent dire un et un seul nom de couleur. Quand tous auront parlé, combien au maximum de personnes pourront connaître à coup sûr la couleur de leur chapeau ?

  Eh bien tous sauf un peuvent le savoir, s'ils se mettent d'accord au préalable sur la stratégie à adopter !

  Maintenant imaginons qu'il y ait plusieurs couleurs, voir une infinité, et pourquoi pas, une infinité de fêtards, que se passe-t-il ? En utilisant des mathématiques de plus en plus sophisitiquées (arithmétique élémentaire niveau collège, groupes, espaces vectoriels puis théorie des ensembles), l'auteur généralise peu à peu le résultat...

  Par Florent Benaych-Georges, Maître de conférences en Mathématiques, Université Paris 6 et École Polytechnique.

  Prérequis :

  • première partie : pas de prérequis
  • deuxième partie : arithmétique niveau terminale S.
  • troisième partie : groupes abéliens.
  • quatrième partie : théorie des ensembles (niveau licence).
  
  

  Importer le texte au format ps ou pdf.

Logique, fondements des mathématiques :

• Les axiomes de Zermelo-Fraenkel

  La théorie des ensembles est entre autres choses une tentative de formalisation, dans un système d'axiomes assez simples et si possible intuitifs, de l'ensemble des connaissances mathématiques. En particulier, l'essentiel de l'arithmétique ou de l'analyse se déduirait de façon élémentaire, quoique assez longue, de cette axiomatique.(par Thomas Chomette)
  

  Prérequis :

  • Aucun, si ce n'est la notion de quantificateur.
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• Construction des entiers naturels

  Nous présentons ici une définition et l'étude des propriétés élémentaires de l'ensemble des entiers naturels, définis dans le cadre axiomatique de la théorie des ensembles. Nous utilisons ces propriétés sans y penser, elles nous semblent évidentes... Mais peut-être méritent elles parfois que l'on s'y attarde quelque peu ? (par Jean Gounon, professeur au lycée Camille Sée)
  

  Prérequis :

  • Le langage et les axiomes les plus courants de la théorie des ensembles (voir par exemple le texte "Les axiomes de Zermelo-Fraenkel").
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

  Entiers relatifs

  Ayant construit les entiers naturels, quoi de plus naturel que de passer aux entiers relatifs. Là aussi, la présentation choisie est la plus axiomatique et rigoureuse possible. Partant de la définition des relatifs, vus comme des classes d'équivalence pour une relation d'équivalence bien choisie sur les couples d'entiers naturels, on en arrive peu à peu jusqu'à l'arithmétique élémentaire. (par Jean Gounon, professeur au lycée Camille Sée)
  

  Prérequis :

  • Relations d'équivalence, ensemble quotient.
  • Propriétés courantes des entiers naturels (voir plus haut)
  • Notion d'idéal dans un anneau. Idéaux principaux. Fiche de rappels en version ps ou pdf.
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

  Nombres rationnels

  Dans la droite ligne des constructions précédentes, nous construisons ici l'ensemble des rationnels, à partir d'une relation d'équivalence sur les couples de relatifs. Nous définissons les opérations plus et multiplier sur ce nouvel ensemble, la relation d'ordre, etc, en montrant que tout ceci prolonge en réalité les opérations déjà définies pour les relatifs.(par Jean Gounon, professeur au lycée Camille Sée)
  

  Prérequis :

  • Relations d'équivalence, ensemble quotient.
  • Propriétés courantes des entiers relatifs (voir plus haut)
  • Structures de groupe, d'anneau, de corps.
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

  Nombres réels

  Ayant construit les rationnels, voici bien sûr les réels, par la méthode des suites de Cauchy. Comme pour les rationnels, il faut vérifier que le nouvel ensemble étends celui des rationnels, et que les opérations, la relation d'ordre, la valeur absolue, se prolongent à l'ensemble des réels.
  Puis, sans bien sûr épuiser le sujet, nous nous penchons sur les propriétés topologiques de l'ensemble des réels : complétude, propriété de la borne supérieure ; propriétés qui sont à la base de toute l'analyse réelle. (par Jean Gounon, professeur au lycée Camille Sée)
  

  Prérequis :

  • Relations d'équivalence, ensemble quotient.
  • Groupe, anneaux, corps. Idéaux dans un anneau.
  • Propriétés courantes des rationnels (voir plus haut)
  • Manipulation de suites, définition précise de la notion de convergence (tous les outils nécessaires sont introduits, cependant une certaine habitude des manipulations de suites permettra de voir plus rapidement les démarches qui fondent quelques démonstrations inévitablement techniques).
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

  Nombres complexes

  Reste encore un pas à franchir dans nos extensions d'ensembles de nombres. Certaines équations algébriques extrêmement simples, à coefficients réels, restent sans solution réelle (par exemple, les réels négatifs ne sont pas les carrés de réels). D'où la nécessité d'étendre encore une fois notre ensemble de nombres, en formant un sur-corps du corps des réels, dont les éléments seront appelés nombres complexes. Ce sur-corps se révélera algébriquement clos, c'est-à-dire que cette fois toute équation algébrique (à coefficients complexes) aura des solutions (complexes).
  Le premier texte défini l'ensemble des complexes, et motive cette construction en montrant par des moyens élémentaires que l'on a des solutions à toute équation de degré deux. Le deuxième, assez technique, introduit la notion d'argument, nécessaire au troisième et dernier texte, dont l'objet est de montrer la clôture algébrique de C. (par Jean Gounon, professeur au lycée Camille Sée, et Thomas Chomette)
  

  Prérequis :

  • Premier texte : structure de corps.
  • Deuxième texte : propriétés des séries entières, manipulation de séries. Fonction d'une variable complexe, dérivation.
  • Troisième texte : notion de compacité. Développements limités. Écriture trigonométrique d'un complexe.
  
  

  Nombres complexes (ps ou pdf), argument d'un nombre complexe (ps ou pdf), clôture algébrique de C (ps ou pdf).

  Pour revenir au sommaire :

  Quaternions

  C'est en essayant de trouver une multiplication sur les triplets de réels (la multiplication sur les complexes correspondant à une multiplication sur les couples de réels) qu'Hamilton découvrit en 1843 les quaternions sur le "Brougham Bridge" à Dublin, gravant sa découverte sur une pierre du pont. L'obstacle majeur était que les quaternions sont en fait représentés par des quadruplets (et non des triplets) de réel, ce qui fait en réalité du corps des quaternions une extension de celui des complexes, même si on perd au passage la commutativité de la multiplication.
  Après avoir construit le corps des quaternions de la façon la plus élémentaire possible, nous étudions les relations entre ceux-ci et les rotations dans l'espace à 3 dimension. (d'après Jean Gounon, professeur au lycée Camille Sée)
  

  Prérequis :

  • Opérations sur les réels et les complexes (voir textes correspondants).
  • Structures algébriques (corps, algèbre, espace vectoriel).
  • Applications linéaires et représentation matricielle, isométries vectorielles (rotations, symétries).
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

  De l'anti-symétrie au centre du corps des quaternions, une remarque sur les relations entre multiplication des quaternions et produit vectoriel (par Nik Lygeros, Université de Lyon I). Version ps ou pdf.

• Ordinaux

  Nous introduisons la notion d'ordinal de la façon la plus élémentaire possible, afin d'en présenter quelques propriétés, qui nous ont paru les plus importantes. Nous ne prétendons pas en faire une étude complète : par exemple, nous passons sous silence les notions d'addition, de multiplication ou d'exponentiation ordinale, qui sont des notions plus difficiles qu'il n'y paraît et mériteraient plus de travail. (d'après Jean Gounon, professeur au lycée Camille Sée)
  

  Prérequis :

  • Le langage et les axiomes les plus courants de la théorie des ensembles (voir par exemple le texte "Les axiomes de Zermelo-Fraenkel").
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• Cardinaux

  Dans ce texte, nous allons présenter la théorie des cardinaux, du moins son début : définition, cardinal d'un ensemble et théorème de Cantor-Bernstein, addition et multiplication cardinale. En revanche, nous passerons sous silence le problème de l'exponentiation cardinale, qui est autrement plus compliquée. (d'après Jean Gounon, professeur au lycée Camille Sée)
  

  Prérequis :

  • Le langage et les axiomes les plus courants de la théorie des ensembles (voir par exemple le texte "Les axiomes de Zermelo-Fraenkel").
  • Notion d'ordinal (voir par exemple le texte sur les Ordinaux).
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :

• La construction des Réels par les coupures de Dedekind

  Nous avons déjà vu une construction du corps des Réels dans ce site (voir ci-dessus). Nous en donnons une autre, moins complexe et moins universelle, fondée sur la relation d'ordre naturelle des rationnels.

  Cette construction a l'avantage de donner très facilement la densité des rationnels dans les réels, mais est en revanche plus laborieuse en ce qui concerne les opérations algébriques. A vous de choisir (vous pouvez prendre les deux !)

  Par ailleurs, elle peut être utile pour les concours de recrutement.

  Par Jean Gounon, professeur de mathématiques.

  Prérequis :

  • Les prérequis de ce texte ont trait au langage : nulle théorie n'est nécessaire, mais il utilise le langage de la théorie des ensembles l'algèbre générale, à un niveau Licence.
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :


 

Histoire et épistémologie des Mathématiques :

• Laplace, Turing et la géométrie impossible du "jeu de l'imitation"

  Dans un article de 1950, devenu justement célèbre, Alan Turing propose, en vue d'opérer une comparaison fonctionnelle entre le cerveau et la machine, un jeu qu'il appelle "jeu de l'imitation". Cet article fut un pas décisif dans le domaine de la philosophie de la connaissance.
  Le texte que nous vous proposons présente un point de vue cognitif sur la question de la différence entre la pensée humaine, continue, et le fonctionnement d'une machine à états discrets. (Par Giuseppe Longo, Directeur de Recherche en informatique théorique, CNRS et ENS.)
  Ce texte a été publié dans la revue Intellectica, n. 35, 2002/2, pp. 131-162, nous remercions l'auteur pour son amabilité.
  

  Prérequis :

  • Le texte n'est pas technique et les seuls prérequis sont une certaine culture scientifique générale.
  • Une connaissance générale des fondements de la théorie des ensembles et de l'arithmétique (telle qu'ils sont exposés dans les textes de la section "Logique" du site) sera utile.
  • Ce texte ouvrant une direction inhabituelle dans notre travail, n'hésitez pas à nous donner votre avis ou à nous demander des précisions.
  
  

  Importer l'article au format ps ou pdf.

  Pour revenir au sommaire :

• Carl Friedrich Gauss, le Prince des Mathématiciens

  C. F. Gauss est toujours considéré par certains comme le plus grand mathématicien de tous les temps. Sa capacité calculatoire hors du commun, couplée à son goût pour la contemplation des idées abstraites l'on amené à résoudre des problèmes (parfois vieux de millénaires !) et à envisager avec une clarté géniale (bien qu'inquiète) les idées qui feraient les mathématiques du futur.

  Mais il fut également un astronome et un physicien de tout premier plan, grâce à ses va-et-vient incessants entre expérience et théorie. Scientifique complet, il n'en fut pas moins homme et eut sa part de drames personnels, dans une période fort troublée de l'histoire de l'Europe : la première moitié du XIX° siècle.

  Dans ce dossier, nous vous proposons la biographie d'un homme de génie, qui transcenda les frontières entre les sciences. A l'aspect biographiques nous avons ajouté des remarques mathématiques dont certaines pourraient faire l'objet d'études en classe. (Par Farouk Boucekkine, ENS)

  La confection de ce dossier doit beaucoup au livre de Simon Gindkin histoires de mathématiciens et de physiciens, traduit en Français par Jean-Michel Kantor aux éditions Cassini. Nous vous recommandons vivement de consulter leur catalogue !

  Par ailleurs, pour la question de la construction de polygones réguliers à la règle et au compas, évoquée dans ce texte, nous vous conseillons de consulter le dossier Construction des polygones réguliers, où elle est traitée in extenso.

  Prérequis :

  • Aucun.
  
  

  Importer l'article au format ps ou pdf.

  Pour revenir au sommaire :

  Le prix Steiner

  Par Lazare Georges Vidiani, Professeur de Mathématiques.

• Résumé - Cet article a été publié dans la revue Quadrature ("Magazine de Mathématiques pures et épicées") numéro 56 AVRIL JUIN 2005 P 30-31. L'éditeur EDP nous a autorisé à le reproduire sur le site culture Math et nous l'en remercions. Voici un lien vers le site de Quadrature http://www.edpsciences.org/journal/index.cfm?edpsname=quadrature

  Dans l'article sur les intégrales de Coxeter, nous avons évoqué, le parcours exceptionnel du mathématicien suisse autodidacte Ludwig Schläfli. Il reçut le prix Steiner en 1930, pour sa découverte -avant Juel- des 27 droites d'une surface cubique non réglée (voir sur le site culture math, un excellent et audacieux article sur ce sujet). Le but de cet article est de rendre accessible la liste exhaustive des lauréats de ce prix, qui furent tous des savants d'envergure internationale.

  Importer l'article au format pdf

  Pour revenir au sommaire :

   

  Mécanique et cinématique

  Compte de rebonds

  Daniel Goffinet, Professeur de Mathématiques.

  Résumé - Il s'agit d'un surprenant problème de collision qui a fait l'objet du "problème du mois" d'avril 2007: se présentant comme de la mécanique, il se révèle être un moyen (peu efficace!) de calculer Pi. La solution peut être obtenue par des méthodes géométriques ou algébriques. L'article comprend:

  • une partie de préliminaires qui précise les conditions du problème.
  • deux parties de découpages en sous questions, l'une géométrique, l'autre dans l'esprit de l'algèbre linéaire
  • une solution purement géométrique" (répondant aux questions de la partie géométrique)
  • une solution par l'algèbre linéaire (répondant aux questions de la partie linéaire)
  • une hypothétique preuve d'impossibilité informatique
  • une hypothétique preuve d'impossibilité physique

  Importer l'article en version pdf [158 Ko, 14 pages]

  Retour au sommaire

  La toupie Tippe-Top

  Lazare Georges Vidiani, Professeur de Mathématiques. Résumé - En 1952, dans le commerce des jouets, quand celui ci proposait des objets instructifs et éveillant questions et imagination, humour et habileté manuelle (Wondergraph, père la colique, etc), -contrairement à notre période où les jeux se réduisent à des peluches ou des touches de commande életronique-, une petite toupie en plastique faisait fureur chez les enfants et les adultes d'esprit jeune. Il s'agissait d'une toupie appelée Tippe-Top, de révolution, constituée de deux parties: l'une était une calotte sphérique d'axe z'z, et l'autre un cylindre d'axe z'z emmanché perpendiculairement au plan de la calotte sphérique, l'ensemble formant un seul solide. L'originalité de la toupie ainsi formée est qu'une fois lancée, elle se retourne sur son manche, en continuant de tourner. Son mouvement fascina même les deux prix Nobel de physique Pauli et Bohr : http://www.fysikbasen.dk/TippetopENGLISH.php Une revue scientifique grand public eut le malheur et l'inconscience de prétendre que cette propriété ne pouvait se justifier scientifiquement : l'année suivante cette toupie faisait l'objet de la partie V du problème d'Agrégation de Mécanique rationnelle 1953, dont l'auteur était Luc Gauthier. Gérard Egheter, dont le site donné bas de colonne 1 de la page 9 de l'article vaut le détour, m'a communiqué le corrigé manuscrit de Jean Frédéric Auguste Delsarte, que sa fille m'a autorisé à reproduire. Ce Normalien (Ulm 1922) fut notamment quatrième à l'Agrégation 1925, membre du groupe Bourbaki, fut Doyen de la faculté des Sciences de Nancy, et dès 1947 il conçut une douzaine de problèmes de concours très originaux pour l'époque (et la nôtre....) en particulier celui des Mines de Nancy 1947 dont vous aurez l'essentiel en allant voir sur culture math, l'article (excellent) loi de groupe sur une surface. Le corrigé est dans le TAPE donné en lien (Tiré A Part Electronique aimablement autorisé par le Directeur Olivier Courcelle de la Revue Quadrature 59 (Janvier Mars 2006) "Revue des mathématiques Pures et Epicées) ; Culture Math remercie l'éditeur EDP qui l'a autorisé à diffuser l'article sur le site CultureMath. Voici, en remerciement, un lien vers le site de Quadrature http://www.edpsciences.org/journal/index.cfm?edpsname=quadrature

  Importer l'article en version pdf [404 Ko, 18 pages]

  Liens

  Une bonne animation, valant mieux qu'un long discours rasant allez voir en http://public.planetmirror.com/pub/irtc/anims/2001-04-15/tippetop.mpg ou encore mieux localisé sur une assiette http://www.science.unitn.it/~karwasz/toys/files/mech/baczek_wst-fr.html. (Faire un click sur les cases d'animation, puis click droit et cocher dans le menu qui apparait "diffuser dans real Player").

  Petite anecdote historique : L'inventeur (1950), le danois Werner Ostberg raconte qu'il a eu l'idée de la toupie tippe top, en observant, dans la jungle sud-américaine, que lorsqu'on coupe le fond d'une calebasse http://fr.wikipedia.org/wiki/Calebasse, il présente, si on le fait tourner, les mêmes propriétés que le tippe-top En fait c'est une re-découverte (voir l'historique page 2 de .http://www.fysikbasen.dk/TippetopENGLISH.php) car l'objet date de 1890 (John Perry) et 1891 (Helene Sperl), si l'on n'accepte pas d'anticiper dès le début des années 1800 par l'étude des anagyres par Sir William Thomson et Hugh Blackburn.

  Sur CultureMath

  Arc en ciel, soucoupes volantes, toupies, courbes elliptiques, et tout ça, par Michèle Audin (2004)

  Voir aussi

  Le cas de Kowalevski, par Michèle Audin (2006) - Ce que les mathématiciens appellent, depuis 1888, « le cas de Kowalevski », c’est une sorte de gyroscope, un genre de toupie si l’on préfère, dont la découverte a ouvert quelques portes sur des allées des mathématiques que l’on n’a pas fini d’explorer.

  Mon choix de Sophie, par Michèle Audin (2006) - Un article sur Sophie Kowalevski, son image, sa toupie et sa réputation scientifique.

  Retour au sommaire

   

  Mathématiques pour les sciences physiques et les sciences de la nature

  Calcul Tensoriel. Application à la relativité.

  Jean Gounon, lycée Camille Sée, Paris

  Résumé: Ce texte a pour objectif de présenter, de la façon la plus simple possible, les fondements mathématiques de la théorie de la Relativité (surtout générale) ; ces fondements constituent les bases de la branche des mathématiques appelée Calcul Tensoriel. A l'inverse des présentations habituelles qui, centrées sur la Relativité, donnent une liste rapide de quelques définitions et résultats pratiques indispensables de calcul tensoriel, cette étude s'intéresse avant tout aux bases mathématiques de la théorie physique qu'est la Relativité. Cette dernière n'est envisagée ici que du point de vue de son articulation avec la théorie mathématique qui la précède ; elle n'est donc pas développée pour elle-même : nous renvoyons, pour son contenu et la révolution qu'elle a apporté en physique, aux nombreux livres et sites consacrés à ce sujet.

  Livres

  • Balian  Roger, Le Temps et sa flèche, Édité par E. Klein et M. Spiro, Flammarion, 1996. (Collection Champs).
  • Einstein  Albert, La Théorie de la relativité restreinte et générale, Dunod, 2004.Une introduction accessible aux théories relativistes.
  • Simon  Yvan, Relativité restreinte, cours et applications, Vuibert, 2004. L’ouvrage de référence en langue française, certes de niveau licence mais au formalisme limité et toujours judicieusement introduit. Les discussions sur l’optique classique et sur l’expérience de Michelson sont remarquables.
  • Collectif, L'ère Einstein, Pour la Science, décembre 2004.
  • KahaneJean-Pierre, Le mouvement brownien comme objet mathématique, Revue du palais de la Découverte, décembre 2004.
  • Jean-Marie Vigoureux, La quête d'Einstein, éditions Ellipses, 2005.

  
  

  Importer l'article en version pdf.

  Pour revenir au sommaire :

  Pourquoi les équations aux dérivées partielles interviennent-elles en biologie ?

  Ce texte est une introduction rapide aux problématiques qui se posent aux mathématiciens qui s'intéressent à la biologie. Partant d'une interrogation légitime ("Les maths peuvent-elles être efficaces en biologie ?"), il se concentre ensuite sur la description d'un exemple d'application intéresante, la modélisation du chimiotactisme chez certaines amibes, montrant à la fois l'intérêt du langage mathématique, et les difficultés qu'on peut avoir pour résoudre un problème aussi complexe qu'un problème de biologie.

  Ajoutons que ce texte est une petite expérience mathématico-informatique puisqu'il inclut des formules (sous la forme de ficiers .gif) et des liens hypertexte vers un début de glossaire. Par conséquent, n'hésitez pas à nous écrire si vous avez des problèmes techniques en le lisant (à ce propos, il est préférable de le consulter avec Internet Explorer ou Mozilla, car Netscape et Safari ont du mal à aligner les images correctement avec le texte !)

  Enfin, ajoutons que ce document est le point de départ d'un dossier "Maths et Bio", qui s'étoffera dans les mois à venir. N'hésitez pas à nous faire des commandes !

  Par Hatem Zaag, chargé de recherche CNRS à l'Ecole Normale Supérieure.
  
  

  Prérequis :

  • Notion de dérivée (les dérivées partielles sont expliquées en annexe)
  
  

  Cet article est disponible sous format HTML.

  Pour revenir au sommaire :

  Équation de la chaleur : traitement numérique.

  L'équation de la chaleur est à l'origine de nombreux problèmes, souvent difficiles, et a fait couler beaucoup d'encre. Nous nous restreignons ici à un cas particulier, avec des conditions de départs assez simple, de sorte que la solution exacte soit connue. Celle-ci va nous permettre d'apprécier l'efficacité (ou les défauts) des méthode numériques de résolution approchée. On montrera et on expliquera à travers cet exemple les différences fondamentales entre méthodes implicites et explicite. Texte accompagné de simulations numériques en java. Les algorithmes sont également déclinés et mis à disposition en version matlab et scilab (scilab est un logiciel libre distribué par l'INRIA, que l'on peut télé-charger ici).
  Par Thomas Chomette, avec l'aide d'Emmanuel Grenier, ENS Lyon.
  

  Prérequis :

  • Éléments de calcul différentiel (fonction de deux variables, dérivée partielle).
  
  

  L'article seul, en version ps ou pdf. Illustrations numériques et programmes, disponibles en version html.

  Pour revenir au sommaire :

  Détermination du sexe selon la température chez les crocodiles

  Saviez-vous que le sexe des crocodiles n'est pas déterminé génétiquement dès la conception, comme c'est le cas pour nous autres mammifères ? En fait, si l'œuf est pondu près de l'eau, dans une terre humide et donc fraiche, il donnera une femelle, s'il est pondu sur une terre sèche et donc plus chaude, il donnera un mâle ! Bien entendu, un milieu "intermédiaire" donnera des résultats intermédiaires...

  Cette spécificité a permis aux crocodiles de survivre quelques centaines de milions d'années aux catastrophes qui ont fait diparaître nombre d'autres espèces.

  Ce texte nous donne un modèle mathématique pour étudier l'évolution d'une population de crocodiles, et comparer cette évolution à celle d'une population où la détermination du sexe se fait génétiquement.

  Par Sylvain Arlot, élève de l'Ecole Normale Supérieure.
  

  Prérequis :

  • Equation différentielles linéaires. Les équations apparaissant dans le textes sont compliquées et non linéaires, mais leur résolution n'est pas l'objectif du texte, qui obtient essentiellement des informations qualitatives sans utiliser de technique excédant la première année de DEUG.

  Importer l'article, en version ps ou pdf.

  Pour revenir au sommaire :

  Interactions entre espèces, modèle de Lotka-Volterra

  Nous nous intéressons ici à un modèle d'interaction proies-prédateurs, proposé par Volterra après la première guerre mondiale. Il s'agissait alors d'expliciter la dynamique des populations de sardines et de requins en mer Adriatique ; expliquer notamment pourquoi les quantités de sardines pêchées après l'interruption due à la guerre n'étaient plus aussi importantes que précédemment et pourquoi à la reprise de la pêche la proportion observée de requins avait augmenté.
  C'est l'occasion d'une étude qualitative assez complète de certains systèmes différentiels. Le texte proprement dit est accompagnés de simulations numériques (applets java). Les programmes utilisés sont également disponibles, commentés, en version matlab et scilab (scilab est un logiciel libre distribué par l'INRIA, que l'on peut télé-charger ici).
  D'aprés un article de Vincent Calvez et Xavier Lafon, ENS (article intégral disponible sur le site du groupe de travail Mathématiques-Biologie). Illustrations de Thomas Chomette.

  Prérequis :

  • Une vague connaissance du langage des équations différentielles suffit pour la première partie.
  • La dernière partie, plus technique, nécessite une certaine familiarité avec des notions de linéarisation (matrice jacobienne), de perturbations, de stabilité, et un peu d'algèbre linéaire.

  L'article seul, en version ps ou pdf. Illustrations numériques et programmes, disponibles en version html.

  Pour revenir au sommaire :

  • Equations de Maxwell et formes différentielles, vers la relativité restreinte

    Ce texte a pour but de présenter les formes différentielles, objet très important dans les mathématiques et la physique moderne, à travers une application classique : la reformulation des Equations de Maxwell (qui modélisent l'électromagnétisme) sous une forme plus compacte et décrivant mieux les symétries observées expérimentalement des champs électrique et magnétique.

  Il n'y a pas d'exposé général dans ce texte, qui ne parle que du cas des dimensions 3 et 4, mais les objets et les méthodes présentés ici sont asiément généralisables à une dimension finie quelconque.

  Par Thierry Levy, chercheur CNRS à l'ENS.

  Prérequis :

  • Intuition de ce que sont les phénomènes électriques et magnétiques.
  • vecteurs de l'espace, base orthonormée directe.
  • symétries de l'espace
  • La connaissance de l'algèbre linéaire au niveau Licence est souhaitable pour être à l'aise avec les objets présentés, mais tout ce qui est nécesaire à la compréhension du texte est défini et exposé.
  
  

  Importer l'article en version ps ou pdf.

  Pour revenir au sommaire :