Les statistiques sont souvent considérées par les lycéens (et parfois par leurs professeurs !) comme une branche mineure des mathématiques, voire prises avec dédain pour un ensemble de recettes loin de la rigueur habituelle de cette science. L'objectif de ce texte est de montrer, sans entrer dans les détails que cet a priori est faux
Pourtant, les statistiques se fondent sur des mathématiques très abstraites et sont en plein essor de nos jours, dans des domaines aussi divers que la sociologie, la finance et la médecine. Parmi les applications usuelles des méthodes statistiques, citons en vrac :
- Déterminer si la canicule a entraîné
une réelle surmortalité.
- Fixer le prix des polices d'assurance.
- Détecter ceux qui trichent sur les montants
qu'ils déclarent aux services fiscaux.
- Avoir dès 20h (et avant le dépouillement
total), le gagnant d'une élection.
- Pouvoir planifier la construction des
crèches et écoles, le nombre d'enseignants à recruter au concours.
- Savoir si le climat change... ou pas
Malgré la diversité de ces exemples, une méthodologie générale se dégage.
- Statistique descriptive :
Il s'agit de la collecte et de l'organisation des données, afin de les représenter d'une manière exploitable. Cette partie nécessite peu de méthodes mathématiques poussées (moyennes, écarts-types, répartitions en classes...).
Exemples : recensement, tableaux de l'INSEE, graphiques-camembert, et bien sûr sondages divers...
- Modélisation :
Une fois collectées, ces données servent à établir un Modèle du problème, c'est à dire choisir un nombre réduit de paramètres permettant de décrire au mieux les données, ainsi que la manière dont elles s'organisent (loi.)
Ici, les fondements mathématiques sont beaucoup plus poussés (probabilités discrètes ou continues, théorie de la mesure...), en effet, il est très facile de construire des modèles incohérents tant l'intuition a tendance à se tromper dans les questions de probabilités !
En particulier, il faut trouver un compromis entre la bonne description et le nombre réduit de paramètres, ce qui n'est pas toujours aisé. les mathématiques nous aident alors à éviter des erreurs fondamentales comme de négliger des données ou d'en surinterpréter d'autres.
Exemples : Nombre d'enfants par femme, courbes de taille et poids... Pour analyser ces données, on considère que de telles données se répartissent suivant une loi discrète.
Autre exemple : les sondages portant sur une question politique considèrent généralement l'appartenance politique du sondé comme un paramètre important, puisqu'il influence sa réponse.
- Statistique décisionnelle :
C'est l'objectif final ! S'appuyant su les deux étapes précédentes, on veut obtenir des résultats prospectifs afn d'optimiser ses ventes, l'efficacité d'un médicament, établir l'impact d'un phénomène (les téléphones portables sur la santé, par exemple)...
Exemple : à partir d'études expérimentales, on va pouvoir évaluer un nouveau traitement médical (cf. paragraphe suivant).
Il est à constater que pour la majorité du Grand Public, les statistiques s'arrêtent à la première étape, suivant la croyance quasi-institutionnalisée que "les chiffres parlent d'eux-mêmes !".
Pourtant, l'essentiel du travail du statisticien se situe plutôt dans les deuxième et troisième étapes. C'est en effet à ce niveau que s'effectue la réflexion, et l'utilisation de méthodes complexes basées sur des notions mathématiques abstraites.
En particulier, il est capital de comprendre que le résultat d'une étude statististique est une fourchette, et non pas un résultat précis. L'amplitude de cette fourchette est déterminée au cours des étapes 2 et 3, de même que les conditions de validité des résultats annoncés.
Il est finalement dommageable pour tout un chacun que cet aspect soit presque entièrement occulté de la culture scientifique "de base" du citoyen, qui, par conséquent peut être manipulé par des sondages dont on ne donne que le résultat moyen... Et réciproquement, un sondage est donné "vrai à 95%", et l'opinion publique crie au scandale lorsqu'on tombe dans les 5% d'erreurs inévitables !
Dans la question très sensible du traitment des maladies graves, au premier chef desquelles les cancers, les statistiques sont des outils intellectuels pour pouvoir étudier rigoureusement l'évolution globale des malades et l'impact des traitements.
Plusieurs questions naturelles se posent :
- Comment modélisation les rechutes cancéreuses ?
Pendant 5 ans, on enregistre le moment de la première rechute de n individus dont le cancer a été traité. On groupe les données en 10 paquets, correspondant aux 10 semestres écoulés.
Le nombre de rechutes à la fin du semestre j est modélisé par un nombre
![$p_j \in [0,1]$](introStats001.gif)
,
au sens où l'on considère que chaque individu a (indépendamment
de ce qui se passe pour les autres) une probabilité 
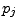d'avoir connu une rechute pendant le semestre j. - Comment évaluer un nouveau traitement ?
La modélisation précédente a été obtenue avec les relevés faits sur les traitements actuels.
On prend un groupe de n malades, à qui on propose le nouveau traitement. On mesure les rechutes pendant 5 ans : soit
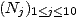la suite du nombre de rechutes. - Cette suite est-elle ``conforme'' au modèle ?
Le modèle nous donne l'espérance (c'est à dire la moyenne) du nombre de rechutes au semestre j: c'est
.
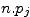Mais bien plus, le modèle nous dit comment
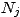doit fluctuer autour de la moyenne.
En effet, on ne tombe presque jamais exactement sur la moyenne, mais on s'en approche. Le modèle nous donne, en même temps que la moyenne, la manière dont les observations peuvent dévier d'elle.
On dira que le nouveau traitement est meilleur si on observe une déviation
peu probable vers 0. Cette dernière appréciation
est délicate à définir, et repose sur des théories
mathématiques.
NB : ceci est un cas d'école, dans la pratique, on a recours à de nombreux raffinements dépendant de la situation précise.
En résumé, le principe des tests statistiques est le suivant :
On se donne un modèle avec un paramètre inconnu x, on se fixe
deux hypothèses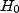 
et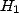 
, et on effectue
un relevé de données.
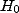est l'hypothèse
à laquelle on est subjectivement attaché.
Elle est par exemple de la forme ``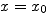
''
(Dans l'exemple précédent : pour tout j,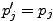 
).
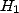serait ici ``x
est différent de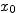 
''
(exemple précédent : il existe j pour lequel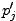 
est différent de 
).
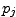Si les données recueillies apparaissent comme peu probables sous le modèle
avec l'hypothèse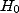 
,
alors on rejette 
.
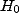Les problèmes apparaissent lorsque les données ne permettent pas de rejeter
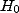. Cela veut simplement
dire que l'on n'a pas encore infirmé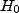 
.
(
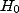pourrait être
fausse, peut-être faut-il simplement un modèle plus précis pour le voir...)
Cas concret : les antennes de téléphonie mobile ont-elles un impact sur la santé ?
Un premier groupe de statisticiens, mandaté par Orange, Bouygues et SFR,
choisit pour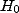 
``Pas
d'impact significatif''.
Un second groupe de statisticiens, mandaté par des associations familiales,
choisit pour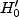 
``Il
existe un impact''.
Imaginons que les données recueillies soient telles qu'aucune des deux
hypothèses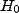 
et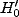 
ne puisse être rejetée. Qu'en conlure ?
Qu'on ne peut pas conclure ! c'est-à-dire qu'on ne peut ni exlure l'existence d'un impact, ni l'affirmer. Mais un glissement sémantique fera que les opérateurs de réseau crieront qu'il n'y a pas de danger, et les associations écriront que la mort nous guette.
On le voit, le choix de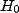 
est politique, de même que l'interprétation des résultats...