Les-mathematiques-du-mouvement

1. Pourquoi cet article ?

Je voudrais essayer de donner une idée du monde abstrait dans lequel j'ai vécu pendant mes années de thèses, en permettant ainsi au lecteur de mettre un pied dans l'univers des mathématiques actuelles. Ce sera l'occasion de présenter rapidement, à travers quelques exemples, la théorie des systèmes dynamiques ; « mathématiques du mouvement », mais aussi mathématiques en mouvement...

2. Les origines : l'étude du mouvement des planètes

On peut attribuer l'origine des systèmes dynamiques aux questions posées par la mécanique céleste, qui cherche à expliquer et prédire les trajectoires des astres.

Au début du XVIIème siècle, à partir de l'observation des planètes, Kepler énonce trois lois qui décrivent leur mouvement. Soixante ans plus tard, Newton et Leibniz inventent simultanément le calcul différentiel ; cet outil permet à Newton de justifier mathématiquement les lois de Kepler. Notamment, si deux corps s'attirent mutuellement selon une force inversement proportionnelle au carré de la distance qui les sépare (comme la force de gravitation), alors leurs trajectoires sont des ellipses situées dans un même plan.

En étudiant la trajectoire de la Lune, qui tourne autour de la Terre tournant elle-même autour du soleil, Newton pose également ce qu'on appelle maintenant « le problème des trois corps » : quelles sont les trajectoires suivies par trois corps célestes en interaction selon la loi de la gravitation ? Il n'obtient pas de réponse à cette question, et soupçonne même le problème d'être inaccessible à l'entendement humain

Au siècle suivant, d'autres mathématiciens reprennent la question. Par exemple, Euler trouve des solutions particulières dans le cas où l'on suppose la masse de la Lune négligeable devant celle de la Terre et du Soleil ; mais le problème général n'est toujours pas résolu.

En changeant radicalement l'angle d'attaque du problème, Henri Poincaré effectue à la fin du XIX^ème siècle un apport majeur. Alors que ses prédécesseurs tentaient (sans succès) de trouver des solutions explicites aux équations de Newton, il se « contente » de chercher les réponses à certaines questions qualitatives sur le comportement des astres. Voici des exemples de questions de cette nature :

- Quelles sont les solutions périodiques, autrement dit µa quelles conditions le mouvement des trois corps se reproduit-il identique à lui-même au bout d'un certain laps de temps ?

- Est-il possible que l'un des trois corps échappe à l'attraction des deux autres en s'en éloignant indéfiniment ?

- Le système est-il « sensible aux conditions initiales » : est-ce qu'un éternuement peut changer de manière fondamentale le comportement futur des planètes ? Attention, si vous attrapez un rhume, vous serez peut-être responsables d'une collision interplanétaire dans quelques milliards d'années... Cette idée est aussi illustrée, dans un autre contexte, par la célèbre image du battement d'ailes de papillon susceptible de déclencher un ouragan à l'autre bout de la Terre !

En renonçant à « tout dire », Poincaré découvre une approche féconde et invente les systèmes dynamiques.

3. Le cadre général

Une des occupations favorites des mathématiciens consiste à expliquer que deux phénomènes qui n'ont, en apparence, absolument rien à voir sont en fait deux cas particuliers d'un même problème. Plus sérieusement, de manière paradoxale, généraliser un problème permet souvent de le résoudre plus facilement, parce que le cadre général fait ressortir les hypothèses essentielles.
Nous allons donc donner une définition générale des systèmes dynamiques. Le passage qui suit est le plus abstrait, et donc le moins facile de ce texte ; nous essaierons ensuite de l'éclairer par des exemples.

Un système dynamique [1] est la donnée :
1. d'un ensemble d'états, noté X, chaque élément x de X représentant une position (ou état) du système ;
2. d'une loi d'évolution (ou transformation) du système : celle-ci associe à chaque état x un « état suivant » noté T(x).
Pour essayer d'éclairer ce langage, revenons un instant au problème des trois corps : dans cette situation, un « état du système » est la donnée des positions dans l'espace et des vitesses de chacun des trois corps. On peut définir une loi d'évolution T de la manière suivante : pour tout état x, T(x) est l'état une seconde plus tard (c'est-à-dire la donnée des nouvelles positions et vitesses).
Face à ces deux objets (ensemble d'états X et loi d'évolution T), le dynamicien se donne un état initial x et étudie la « suite des itérés de x », obtenue de la manière suivante (voir Figure 1 ci-dessous) : le premier itéré de x est T(x) ; le deuxième itéré de x est T(T(x)), noté plus simplement T²(x), autrement dit « l'etat suivant l'état suivant x ». On définit de la même manière, pour tout nombre entier n, le « n ^ième itéré de x » que l'on note Tⁿ(x) : dans le cas des trois corps, c'est l'état du système après n secondes d'évolution.
Le dynamicien s'occupe plus précisément du comportement « asymptotique » (ou « à l'infini ») de cette suite ; voici quelques comportements possibles :

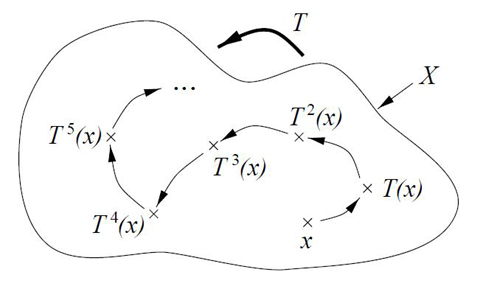Figure 1 : Un système dynamique abstrait

1. Le comportement le plus simple apparaît si x est un « point fixe de T », c'est-à-dire si T(x) = x ; dans ce cas, tous les itérés de x sont égaux à x (le système ne change pas d'état, on dit aussi que x est un point d'équilibre - voir Figure 2 ci-dessous).

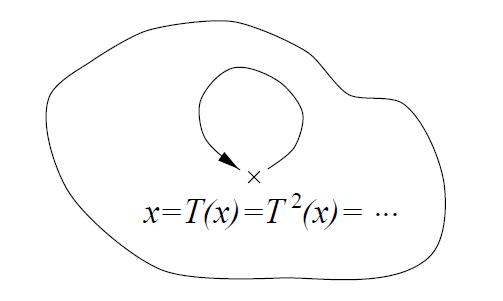Figure 2 : Un point fixe

2. Il peut arriver que le premier itéré de x soit différent de x (l'état n'est pas fixe), mais qu'il existe un itéré ultérieur qui soit égal à x ; cet état est alors dit « périodique « (le système occupe périodiquement les mêmes positions - voir Figure 3 ci-dessous).

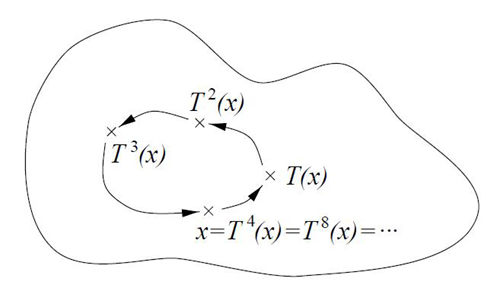Figure 3 : Un point périodique, de période 4

3. Beaucoup d'autres comportements sont possibles : la suite des itérés d'un état peut se rapprocher d'un état d'équilibre, ou d'une suite d'états périodiques, ou bien passer tout prés de tous les autres états du système, ou encore « s'en aller à l'infini » !

4. Des exemples

4.1 Opiluo le Centaurien

Opiluo, de retour vers Alpha du Centaure après une petite virée, tombe en panne sèche à quelques années lumières à peine de chez lui. Pas une station-service en vue : il n'a d'autre solution que d'aller se ravitailler dans le système solaire le plus proche, et Opiluo débarque ainsi sur la troisième planète en partant du petit soleil jaune. Visiblement, le galactique standard n'est pas inscrit au programme des écoles du coin ; encore des régionalistes réfractaires à la galaxisation ! Comme les Centauriens sont des gens logiques et ordonnés, et qu'en plus ils ont tout leur temps puisque le dieu qui les a créés a oublié de les rendre mortels, il décide de commencer par étudier la langue locale. Il met la main sur un vieux dictionnaire, et cherche la signification d'un mot auquel un individu en costume bleu avait l'air d'attacher une grande importance, le mot « papier ». Il lit :

« Matière à base de cellulose, et dont on fait des feuilles qui servent à écrire. »

ce qui ne l'aide pas beaucoup. En remplaçant dans cette expression les mots qui ont l'air importants par leur définition, le sens du mot de départ devrait s'éclairer. Opiluo feuillette à nouveau son dictionnaire, et note :

« Réalité constitutive des corps, susceptible de toutes sortes de formes à base de substance organique du groupe des glucides contenue dans la membrane des cellules végétales, et dont on fait des morceaux de papier sur lesquels on peut écrire qui servent à écrire. »

Bigre ! Peut-être en réitérant le processus ? Il obtient cette fois-ci :

« Existence effective constitutive des parties matérielles d'un être animé, susceptible de toutes sortes d'apparences visibles extérieures d'un objet à base de matière dont une chose est formée organique de l'ensemble de personnes rapprochées dans un endroit des constituants de la matière vivante contenant du carbone, de l'hydrogène et de l'oxygène contenue dans le tissu mince, souple destiné à former des organes des éléments constitutifs de tout être vivant végétaux, et dont on fait des fragments d'un corps solide de matière à base de cellulose, et dont on fait des feuilles qui servent à écrire sur lesquels on peut écrire qui servent à écrire. »

Découragé par la difficulté de cette langue, mais amusé par le procédé, Opiluo décide de rentrer chez lui à tentacules et de lancer la mode des systèmes dynamiques sur Alpha du Centaure, où il vécut heureux et eut une infinité d'enfants... Vous l'avez peut-être deviné, le jeu inventé par le Centaurien [2] est un système dynamique : l'ensemble X des états du système est constitué de toutes les phrases de la langue française ; la transformation T consiste à remplacer tous les substantifs d'une phrase par leur définition dans un dictionnaire donné. Pour Opiluo, l'état initial x était le mot « papier » ; l'état suivant, T(x), est la définition de ce mot ; les deux expressions obtenues ensuite sont les deuxième et troisième itérés de x par la transformation T.

4.2 Un système dynamique mathématique : le SHIFT

Le deuxième exemple est moins anecdotique, et joue un rôle important dans la théorie des systèmes dynamiques.

Description du système. Cette fois-ci, X est l'ensemble des nombres compris entre 0 et 10 (sauf 10) ; la transformation T consiste à supprimer le chiffre avant la virgule et à décaler la virgule d'un rang vers la droite. Par exemple, si on part de l'état initial : x = π ; = 3, 14159265359… alors T(x) = 1, 4159265359… puis T²(x) = 4, 159265359... et cetera (voir Figure 4 ci-dessous).

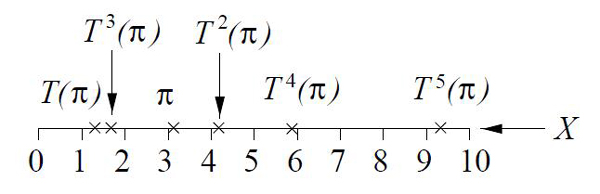Figure 4 : Premiers itérés de π par le SHIFT

Quelques propriétés. Dans ce système dynamique, les points fixes de l'ensemble X sont faciles à trouver : il y en a exactement 10 (quels sont-ils ?...). Les points périodiques ne posent pas plus de problème : un nombre est un point périodique pour la transformation T si la suite des chiffres qui le composent est périodique (on dit aussi qu'un tel nombre est rationnel, c'est- à-dire qu'on peut l'obtenir comme quotient de deux nombres entiers). Par exemple, le nombre y = 3, 3512335123351233512… est périodique, puisque T⁵(y) = T¹⁰(y) = T¹⁵(y) = … = y. Voici une caractéristique intéressante de ce système. Dans le premier exemple, on a pris pour état initial le nombre x = π ;. Choisissons un autre état initial très proche de π ; par exemple sa valeur décimale approchée à un millionième par défaut, x' = 3, 14159200000... ; comparons les itérés successifs des deux états x et x' :

x = 3, 14159265359...
T(x) = 1, 4159265359...
T²(x) = 4, 159265359...
T³(x) = 1, 59265359...
T⁴(x) = 5, 9265359...
T⁵(x) = 9, 265359...
T⁶(x) = 2, 65359...
T⁷(x) = 6, 5359...
T⁸(x) = 5, 359...

x’ = 3, 14159200000...
T(x’) = 1, 4159200000...
T²(x’) = 4, 159200000...
T³(x’) = 1, 59200000...
T⁴(x’) = 5, 9200000...
T⁵(x’) = 9, 200000...
T⁶(x’) = 2, 00000...
T⁷(x’) = 0, 0000...
T⁸(x’) = 0, 0000...

Alors qu'on est parti de deux états initiaux très proches, on obtient au bout de quelques itérations deux comportements très différents : après le 7^ème coup, les itérés de x’ vont rester obstinément sur le 0 tandis que ceux de x vont continuer à osciller indéfiniment... La conclusion est la suivante : on ne peut prédire le comportement à long terme du système qu'à la condition incontournable de connaitre l'état initial avec une précision absolue (c'est-à-dire, dans le cas du SHIFT, connaitre toutes les décimales du nombre de départ) : autrement dit, le système est « sensible aux conditions initiales ».
Un des intérêts du SHIFT est que les mathématiciens savent reconnaitre, dans un certain nombre de systèmes dynamiques, la présence d'un sous-système qui se comporte comme le SHIFT ; toutes les caractéristiques de ce modèle (beaucoup de points périodiques, une zone de sensibilité aux conditions initiales, ...) se retrouvent alors dans les systèmes considérés.

Des statistiques sur les décimales des nombres. A peu prés à l'époque où Poincaré étudiait la mécanique céleste, d'autres savants se penchaient sur le comportement des gaz. Maxwell a formulé le premier ce qu'on appelle « l'hypothèse ergodique » [3] : supposons qu'on enferme une certaine quantité de gaz dans un récipient ; l'énergie totale du gaz, mesurée à un instant donné, est la somme des énergies cinétiques [4] de chacune des molécules du gaz à cet instant (autrement dit, l'énergie macroscopique est la somme des énergies microscopiques). S'il n'y a pas d'échanges de chaleur entre le gaz et l'extérieur (autrement dit si le récipient est thermiquement isolé), l'énergie totale reste constante au cours du temps, par contre l'énergie cinétique de chaque molécule varie sans cesse au gré des chocs contre les autres molécules du gaz et contre les parois du récipient. Dans cette situation, l'hypothèse ergodique affirme que les molécules du gaz vont occuper successivement tous les micro-états de positions et de vitesses compatibles avec l'énergie totale, c'est- à-dire tels que la somme des énergies cinétiques des molécules du gaz soit égale à l'énergie totale. Cette hypothèse sur le comportement microscopique du gaz permet notamment de faciliter le calcul des grandeurs macroscopiques du système : énergie, température, entropie...
Une cinquantaine d'années plus tard (le temps que les outils mathématiques appropriés, notamment la « théorie de la mesure », soient développés), cette idée issue de la thermodynamique donne naissance à un théorème, le théorème ergodique de Birkhoff, et aussi à une nouvelle branche des systèmes dynamiques, la théorie ergodique. Ce théorème permet d'obtenir des renseignements statistiques sur une certaine classe de systèmes dynamiques et notamment sur le SHIFT.

Choisissons un nombre x entre 0 et 10, « au hasard » (une des difficultés de la théorie, sur laquelle nous n'insisterons pas, consiste à donner une signification mathématique précise à ce choix aléatoire d'un élément dans un ensemble qui en contient une infinité ; on dit aussi que les propriétés que nous allons énoncer sont valables pour « presque tous » les nombres entre 0 et 10). Que peut-on dire sur les décimales de x ? Par exemple, y a-t-il des 7 parmi elles ? Si oui, quelle est la proportion de 7 parmi toutes les décimales ? Peut-on trouver quelque part la séquence 123456789 ? Ou bien la date de votre anniversaire ?

Toutes ces questions peuvent être reformulées à l'aide du SHIFT. En particulier, la n^ième; décimale de x est aussi la valeur entière du n^ième itéré de x. On saura donc si l'une des décimales de x est un 7 en regardant si l'un des itérés de x est compris entre 7 et 8. Mieux : on aura la proportion de 7 dans les décimales en comptant la proportion d'itérés de x qui sont entre 7 et 8.

Maintenant que nous avons exprimé ces questions avec le langage de la dynamique, le théorème ergodique accepte de nous répondre. Il affirme que chacun des dix chiffres apparaît une infinité de fois dans la suite des décimales du nombre x, et qu'on les retrouve tous avec la même fréquence : en moyenne, une décimale sur dix est un 7. Encore plus fort, on retrouve aussi n'importe quelle séquence de chiffres une infinité de fois dans ces décimales, dans une proportion qui dépend uniquement de la longueur de la séquence [5] [6] !
On peut aussi exprimer les conséquences du théorème ergodique sur le SHIFT en termes de probabilités (on parle alors de « théorème des grands nombres »). La suite des décimales d'un nombre « choisi au hasard » peut d'abord être vue comme le résultat d'une infinité de lancers successifs d'un dé (à 10 faces, et non pipé !). Le théorème ergodique entraine alors qu'on peut être presque certain que chaque face sortira en moyenne une fois sur dix. Dans le même genre d'idée, prenons un singe qui a l'éternité et un ordinateur avec traitement de texte devant lui, et supposons qu'il se mette à taper indéfiniment au hasard sur le clavier. On peut alors affirmer qu'un jour, le singe tapera les œuvres complètes de Balzac (et aussi, juste après, le texte que vous avez sous les yeux...). Bien sûr, ça lui prendra un sacré bout de temps, et la plus grande partie de sa production n'aura aucun sens, mais tout Balzac y sera en un seul bloc et à la virgule près !

5. Topologie de l'espace des homéomorphismes de Brouwer

Nous pouvons maintenant essayer de donner une (petite) idée de ce qui se passe dans cette thèse. Un « homéomorphisme de Brouwer » est un certain type de système dynamique, dont l'ensemble d'états X est le plan. Une des hypothèses essentielles est qu'il ne doit pas posséder de point fixe : si h est un homéomorphisme de Brouwer, aucun point du plan x ne peut être égal à son premier itéré h(x).

5.1 Des exemples

Les Figures 5, 6 et 7 ci-dessous représentent une courbe comme celles qui sont dessinées (et une seule), et que la transformation consiste à « se déplacer le long de la courbe, dans le sens des flèches, sur une distance de 1 centimètre ».

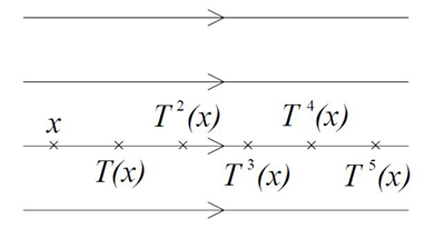Figure 5 : Une translation

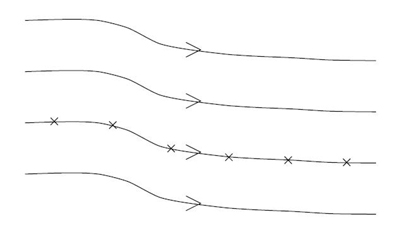Figure 6 : Une translation un peu déformée

Le premier est une simple translation vers la droite. Le deuxième ressemble beaucoup à la translation, puisqu'on peut l'obtenir à partir du premier dessin en déformant un peu la feuille (on peut imaginer que celle-ci est en caoutchouc et qu'on tire la partie droite vers le bas sans bouger la partie gauche) ; on dit qu'il est « conjugué » à la translation. Le troisième, par contre, est différent ; on l'appelle « l'homéomorphisme de Reeb ».

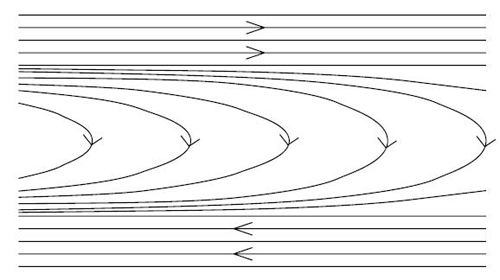Figure 7 : L'homéomorphisme de Reeb

Voici un comportement dynamique qui permet de distinguer la translation de l'homéomorphisme de Reeb : prenons n'importe quel disque du plan, et observons d'abord ce qui se passe lorsqu'on itère la translation (voir Figure 8 ci-dessous).

Figure 8 : Itérés d'un disque par translation

Au bout de quelques itérations, le disque disparaît entièrement du dessin ; on dit que ses itérés « tendent vers de l'infni ». Ceci est aussi vrai pour la translation déformée du second dessin. Par contre, si D est un disque qui rencontre la droite Δ₁ (voir Figure 9 ci-dessous), ses itérés sous l'action de l'homéomorphisme de Reeb « s'accumulent » sur la droite Δ₂.

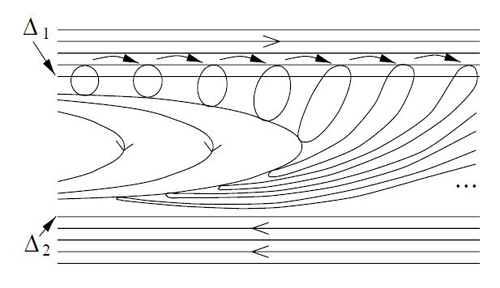Figure 9 : Itérés d'un disque par l'homéomorphisme de Reeb

5.2 Des propriétés remarquables

C'est Brouwer, au début du siècle, qui a étudie le premier ce type de système dynamique [7]. Son résultat principal dit qu'un homéomorphisme de Brouwer h quelconque, même s'il peut être globalement très différent de la translation, lui « ressemble » sur des grands domaines du plan. On peut expliquer facilement un des résultats intermédiaires : sous l'action de h, les itérés de n'importe quel point x du plan « tendent vers l'infini » [8] ; notamment, alors qu'on a supposé seulement l'absence de point fixe (chaque point est différent de son premier itéré), Brouwer démontre qu'il ne peut pas non plus y avoir de point périodique : chaque point est aussi différent de tous ses itérés ultérieurs.

Figure 10 : Encore un homéomorphisme de Brouwer

5.3 Différents sens du mot "forme" : homotopie et topologie [9]

En épaississant un point, on peut obtenir un segment, un carré ou un disque, ou encore un cube (selon le nombre de directions dans lesquelles on étire le point). De même, un anneau ou un tore plein peuvent être obtenus à partir d'un cercle. La théorie de l'homotopie ne considère que les propriétés qui ne changent pas lorsqu'on épaissit un objet : on dira qu'un cube « a le type d'homotopie du point », ou qu'un anneau « a le type d'homotopie du cercle ». Par contre, elle distingue un segment d'un cercle, parce qu'on ne peut passer du premier au deuxième sans effectuer un « recollement », ce qui est interdit.
La topologie, elle, n'autorise pas les épaississements mais seulement les déformations : une étude topologique est plus fine qu'une étude homotopique. Par exemple, un segment a la même topologie qu'un demi-cercle, et un carré (plein) a la même topologie qu'un disque, mais le topologue distingue les segments des carrés.

5.4 Dans la thèse

Les translations (ou les conjugués à la translation) ont un comportement dynamique très simple ; certains articles décrivent par contre des homéomorphismes de Brouwer avec des propriétés dynamiques compliquées. Cette remarque conduit µa se demander s'il est possible de passer progressivement, « continûment », de la translation à n'importe quel autre homéomorphisme de Brouwer. On considère alors l'ensemble de tous les homéomorphismes de Brouwer comme un espace abstrait B dans lequel on cherche les différentes manières de se déplacer ; on aimerait notamment connaître la « forme » de cet espace.
Le principal résultat dit que B a le type d'homotopie du cercle. Cependant, nous n'avons pas réussi à déterminer sa topologie : on peut imaginer B comme un cercle épaissi selon une infinité de directions indépendantes, ce processus d'épaississement n'étant pas encore parfaitement clair.

6. En forme de conclusion

J'ai soigneusement évité, jusqu'ici, d'aborder une question récurrente, LA question posée par tous les non-mathématiciens :

« MAIS A QUOI ÇA SERT ? Autrement dit, comment les mathématiques peuvent-elles nous aider à comprendre le monde dans lequel on vit, à agir sur lui ?

- Voici une réponse possible : les mathématiques sont un langage pertinent pour décrire la réalité. Depuis Galilée, une grande partie des sciences physiques utilise ce langage. Et les physiciens ne se servent pas uniquement des notions mathématiques de base ; la physique théorique nécessite des concepts très abstraits qui posent aux mathématiciens des problèmes complexes.

- Donc, les homéomorphismes de Brouwer servent à résoudre des problèmes physiques...

- A vrai dire, non, pas vraiment. L'utilité des mathématiques est une utilité globale, mais il faut se garder de penser que chacune des questions étudiées est liée à un problème physique. Comme un grand nombre de concepts, les homéomorphismes de Brouwer ont été introduits lors de l'étude d'un problème interne aux mathématiques, et leur étude devient elle-même un nouveau problème qui pourrait faire apparaître de nouveaux concepts qui eux-mêmes...

- Enfin de compte, tu avoues que les homéomorphismes de Brouwer ne serviront jamais à rien, et pourtant tu étudies la topologie de leur espace !

- On ne peut pas dire ça non plus... Les mathématiques sont une science trµes particulière, où chaque problème est relié à beaucoup d'autres, où les passerelles entres les différents domaines sont nombreuses et souvent inattendues. Ainsi, chaque étude peut faire avancer d'autres problèmes et « servir » de manière indirecte. D'autre part, les concepts inventés par les mathématiciens sont souvent très généraux, et ils ont la mauvaise habitude de ressurgir de manière centrale pile à l'endroit où on ne les attendait pas ! En cherchant à obtenir une formule donnant les zéros d'un polynôme de degré 5, on est conduit à étudier l'ensemble des permutations de ces zéros, puis (par généralisation) on invente le concept de « groupe » ; ce même concept s'avère ensuite d'un intérêt primordial dans la mécanique quantique, dans la théorie de la relativité générale ou dans l'étude des symétries des cristaux... Autre exemple, dont nous avons déjà parlé : le théorème ergodique de Birkhoff. L'énoncé est motivé par un problème physique, mais la preuve passe par des concepts mathématiques développés indépendamment ; après quoi le théorème s'applique à des situations physiques aussi différentes que l'étude des gaz, du système solaire ou des billards, et à la statistique sur les décimales des nombres !

- Mais comment on peut être motivé par une utilité aussi lointaine et hypothétique ? !

- On touche là au fond du problème. En fait, le plaisir qu'on ressent à faire des mathématiques n'est pas du tout lié à leur « applicabilité ». Il y a un plaisir purement intellectuel, qui tient à la fois de l'émotion esthétique du créateur et de la soif de découvertes de l'explorateur. Prenons le « paradoxe de Banach- Tarski » : c'est un théorème qui affirme qu'il existe une manière de découper une boule en quatre morceaux, puis de déplacer ces morceaux pour reconstituer deux boules qui ont chacune la même taille que la boule de départ ! ! C'est un résultat qui semble contredire la réalité physique, puisque personne n'a jamais réussi à fabriquer de cette manière deux oranges à partir d'une seule ; pour les mathématiciens [10], ce paradoxe apparent rend le théorème d'autant plus fascinant... Il y a aussi, à un autre niveau, un plaisir ludique dans la manipulation des symboles comme pour les pièces d'un puzzle.

- Alors, en ce sens, c'est une activité artistique particulièrement inaccessible, un peu comme si seuls les musiciens pouvaient ressentir une émotion musicale !

- C'est vrai ; mais peut-être avez-vous malgré tout pris quelque plaisir à l'écoute de cette partition simplifiée ?… »

Bibliographie

George David Birkhoff, What is the ergodic theorem, American mathematical monthly, april 1942, vol 49 p. 222-226.

Jean-Paul Delahaye, Le fascinant nombre π, Bibliothèque « Pour La Science ».

Ivor Grattan-Guinness, The Fontana history of mathematical sciences, Fontana Press, London 1997.

Anatole Katok et Boris Hasselblatt, Introduction to the modern theory of dynamical systems, Encyclopedia of Mathematics and its Applications (vol 54), Cambridge University Press, 1995.

OULIPO, Atlas de littérature potentielle, Folio Essais (poche).

Notes

[1] En fait, la définition correspond aux systèmes dynamiques dits discrets, par opposition aux systèmes dynamiques continus.

[2] Le procédé s'inspire des travaux de l'OuLiPo, groupe de littérature expérimentale fondé par l'écrivain Raymond Queneau et le mathématicien François Le Lionnais.

[3] En l'honneur de Maxwell, elle est aussi appelée « hypothèse de Boltzmann ».

[4] L'énergie cinétique d'un corps est l'énergie qu'il possède du fait de sa vitesse ; c'est aussi l'énergie qu'on peut récupérer en amenant ce corps à l'arrêt : pour stopper sa voiture, un conducteur peut freiner, c'est-à-dire transformer son énergie cinétique en chaleur dégagée lors du frottement des plaquettes de freins sur le tambour, ou bien rentrer dans un mur, auquel cas l'énergie cinétique sert à déformer le mur et la voiture (et éventuellement le conducteur). Cette énergie est égale à la moitié du produit de la masse par le carré de la vitesse.

[5] Le théorème annonce que « presque tous » les nombres possèdent ces propriétés statistiques ; mais pouvez-vous trouver un nombre qui les verité ? Les nombres les plus simples à décrire sont les nombres rationnels, dont la suite des décimales est périodique (voir plus haut). Cependant, ces nombres ne se comportent pas de la manière voulue : considérons en effet un tel nombre z et appelons n la longueur de la séquence de décimales qui se reproduit périodiquement ; alors, par exemple, la séquence composée de n fois le chiffre 1 et d'un 2 n'apparaît pas dans les décimales de z. Au passage, ceci entraîne donc que presque aucun nombre n'est rationnel ! Quant aux décimales du nombre π, bien qu'on en ait calculé 51 milliards, on ne sait pas répondre aux questions statistiques les concernant ; personne ne sait s'il y a une infinité de 7 dans l'écriture décimale du quotient entre le périmètre et le diamètre des cercles...

[6] On peut voir le rapport avec la formulation de l'hypothèse ergodique par Maxwell : en particulier, partant d'un nombre pris au hasard, la valeur entière des itérés sous l'action du SHIFT prend toutes les valeurs possibles, de 0 à 9.

[7] Brouwer espérait que son étude aiderait à résoudre un « problème de Hilbert » concernant les « actions de groupes topologiques » ; en fait, ce problème a par la suite été abordé avec des techniques différentes, et l'étude des homéomorphismes de Brouwer a été poursuivie pour son intérêt propre.

[8] Voici le sens précis de cette expression : si on considère n'importe quel disque D du plan, même très grand, il n'existe qu'un nombre fini d'itérés de x qui sont dans D : au bout d'un certain nombre d'itérations, on n'obtiendra plus que des points à l'extérieur du disque.

[9] Les définitions formelles de ces notions étant assez compliquées, les explications qui suivent sont nécessairement très schématiques.

[10] Ce résultat est « non constructif », parce qu'il annonce l'existence d'un objet qu'il n'est pas possible d'expliciter ; certains mathématiciens (comme Brouwer à certaines périodes de sa vie) refusent de considérer les énoncés de ce type.

Les mathématiques du mouvement Introduction informelle aux systèmes dynamiques