Histoire des mathématiques
|
|
Histoire des mathématiques
|
|
Index des documents |
Pages chronologiques |
Résumés
|
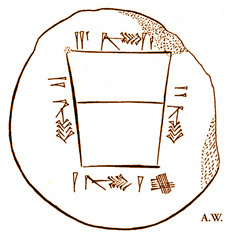 |
par Christine Proust,
Directrice de recherche au CNRS
Résumé - Les plus anciens textes mathématiques connus sont des problèmes d’arpenteurs. Il s’agit de calculer des surfaces de champs, et de partager des parcelles en parts égales. Certains de ces problèmes conduisent à des problèmes arithmétiques fameux : trouver des nombres entiers vérifiant des relations telles que a²+ b²= c² (trouver des triplets pythagoriciens) ou a² + b² = 2c² (trouver des triplets babyloniens). Cet article montre le chemin qui a conduit les anciens arpenteurs de Mésopotamie du calcul des surfaces vers ces problèmes arithmétiques. Il fournit des idées d’activités en classe : Comment partager un trapèze en deux trapèzes de même aire? Comment trouver des triplets babyloniens ou pythagoriciens en base 60? Comment utiliser une figure aussi simple que deux carrés concentriques pour démontrer des résultats qui, autrement, demanderaient des calculs compliqués? |
Autres ressources sur CultureMATH
Articles de Christine Proust Le calcul sexagésimal en Mésopotamie: enseignement dans les écoles de scribes Brève chronologie de l'histoire des mathématiques en Mésopotamie Les numérations anciennes A l'école des scribes de Mésopotamie |
|
 |
Une
conférence de David
Aubin, Professeur de l'université Pierre et
Marie Curie
La conférence ici mise en ligne est l'une des actions concrètes de l'atelier d'histoire des sciences coordonné par Matthieu Husson. Elle est le résultat de la collaboration entre David Aubin avec deux professeurs (physique et SI) du lycée Léonard de Vinci à Levallois-Perret. David Aubin fait une présentation synthétique du développement de la balistique en Europe depuis la fin du moyen âge jusqu'au seuil de la seconde guerre mondiale. |
| Utilistation en classe
- Cette
conférence, donnée devant une classe de seconde
du lycée Léonard de
Vinci à Levallois-Perret, s'inscrit dans le cadre de la
thématique "Science
et investigation policière" de l'enseignement d'exploration MPS,
et peut donc être visionner en classe
dès le collège. |
|
 |
Dossier
présenté par Alain Le Mignot
Présentation - Ce dossier consacré à l'histoire de la logique sera composé de trois articles. Au milieu du XIX° siècle, la vieille logique des philosophes, introduite par l’Organon d’Aristote (-384 - -322) complétée par les Stoïciens puis travaillée sous toutes les coutures de la rhétorique à travers toute la scolastique du Moyen Age, quitte brusquement le lieu qu’elle occupait depuis deux millénaires dans l’ensemble des connaissances. Elle tend à s’éloigner de la philosophie puisqu’elle se métamorphose en une sorte de calcul algébrique qui lui donne une allure fortement mathématique, et ce mouvement sera quasiment achevé à la fin du siècle. A l’évidence, un tel remaniement d’un branche entière du savoir n’est pas commun; aussi il n’est pas sans poser de très nombreuses questions parfois complexes. C’est à quelques unes d’entre elles que nous allons tenter d’apporter certains éléments de réponse. Comment est-il possible qu’un aussi vénérable ensemble de connaissances, considéré par Emmanuel Kant (1724-1804) comme un tout achevé, abandonne ce qui passait pour son 'lieu naturel', lié depuis toujours à la théorie du langage, pour surgir du côté du calcul algébrique alors en plein renouveau ? |
| Pourquoi, alors que leur
science est confrontée à des problèmes
important liés à son développement
même et à sa nature, des
mathématiciens anglais se sont-ils
intéressés à ce qui était
alors
considéré comme une partie de la philosophie pour
la transformer,
semble-t-il, en une branche de l’algèbre ? Comment ce bouleversement a t-il été vécu non seulement par les acteurs, mais aussi par ceux qui se sont trouvés concernés, que leurs intérêts soient littéraires ou scientifiques ? Quelles sont les étapes qui ont été nécessaires pour qu’au début du XX° siècle, c’est à dire en l’espace de cinquante ans, on puisse considérer que la logique est non seulement devenue une partie des mathématiques, mais qu’elle en est le socle ? Utilisattion en classe - Le contenu de ces articles peut sembler trop spécialisé pour des élèves du secondaire qui pourraient être rebutés par les détails. Par contre, on peut les lire très simplement comme une histoire, ou un "conte réel". A ce titre, ils constituent un moyen de montrer que les mathématiques que l'on enseigne, et qui semblent toute ficelées, ne sont pas une brusque révélation. Bien au contraire, elles sont l'aboutissement d'un lent processus d'élaboration historique souvent complexe au cours duquel se mettent peu à peu en place les différentes briques qui constitueront une théorie. On y voit aussi se mêler des intervenants dont les intérêts et les projets sont distincts, voire opposés, mais qui tous apportent leur contribution à l'édifice. En général, ce n'est qu'après que la théorie ait été "lissée" à travers ses applications, et qu'elle fait alors consensus, qu'elle devient l'objet d'un enseignement hors du cercle des spécialistes. |
|
Par André Cauty, Professeur des Universités à Bordeaux 1, équipe CELIA (CNRS) Résumé - Cette approche critique des nombres aztèques et mayas voudrait attirer l'attention des lecteurs sur les principaux systèmes d'écriture du nombre en usage dans l'antiquité mésoaméricaine. Les principaux sont les numérations écrites mayas et aztèques. La numération vigésimale de position des scribes mayas, de l'époque classique et des codex du postclassique, qui l'utilisèrent pour noter les dates dites du Compte long sous la forme d'un nombre à cinq chiffres exprimant, en nombre de jours, la durée écoulée depuis la date origine de la chronologie maya (11/08/-3113). La numération vigésimale additive des scribes aztèques, qui l'utilisèrent notamment pour noter, le plus souvent sous forme de nombres ronds à un ou deux chiffres significatifs, les quantités de tributs que chaque communauté devait remettre à la Triple Alliance. Autre différence, les Mayas écrivaient de nombreuses égalités liant dates et durées, tant de la vie politique des cités que des récits mythologiques. Les Aztèques n'ont pas écrit d'égalités, et ils n'ont même pas laissé de dates en calendrier de l'année vague solaire (l'année mésoaméricaine de 18 x 20 + 5 jours). Par contre, à l'époque coloniale, les Aztèques développèrent de nouvelles formes d'écritures des cadastres, et peut-être des procédés d'approximation des surfaces. Utilisation
en classe
- Dans son analyse comparée des numérations mayas
et
aztèque, l’auteur éclaire quelques
aspects
fondamentaux des numérations orales et écrites,
et livre
ainsi un matériau très riche aux enseignants qui
abordent
en classe, notamment dans les séries littéraires,
l’histoire de la numération.
|
Par Marc Chemillier, Directeur d'études à l'École des Hautes Études en Sciences Sociales (EHESS) Victor Randrianary, anthropologue et vidéaste (CNRS - Musée de l'Homme) Denis Jacquet, psychologue, Maître de conférence (Université de Caen) Marc Zabalia, psychologue, Maître de conférence (Université de Caen) Résumé - La divination sikidy consiste à disposer sur le sol des graines de fano (une sorte d'acacia), sous la forme d'un tableau, dans le but de lire la destinée à travers certaines configurations de graines qui apparaissent dans ce tableau. La procédure de placement des graines comporte une partie produite au hasard (où se manifeste la destinée), et une partie construite à partir de la précédente selon des règles précises. Cette partie calculée du sikidy met en œuvre des propriétés formelles élaborées qui sont celles d'une véritable structure algébrique. Utilisation
en classe
– Faire lire ce texte à des
élèves pourrait permettre de poser une
question fondamentale de l’Ethnomathématique.
Lorsque des activités ne
sont pas identifiées comme étant des
mathématiques par ceux qui les
pratiquent, comment reconnaît-on qu’elles
appartiennent au champ de
cette discipline ? Par quels critères ?
Poser cette question au cours
d’un débat ou par un questionnaire donnerait
l’occasion aux élèves de
s’interroger sur leur propre vision des
mathématiques.
|
Page web de Marc Chemillier
Site geomance
Par Massimo Galuzzi, Université de Milan Résumé - Le problème de Pappus parcourt l'entière carrière scientifique de Newton. La solution de ce problème lui fournit une occasion précieuse pour mettre à l'épreuve les résultats de géométrie projective qu'il élabore progressivement à partir des années de sa jeunesse. Mais il oppose souvent ses solutions à celle donnée par Descartes en opposant la « vraie » analyse des Anciens aux déformations générées par l'usage aveugle de l'algèbre. De plus, il est un
peu
étonnant que Newton ait toujours
considéré ce
problème comme équivalent à celui de
tracer une
conique par cinq points, en supposant (tacitement) qu'une
région
du plan soit choisie par avance. C'est une attitude bien
différente de celle qui anime les discussions entre
Descartes,
Roberval, van Schooten et Huyghens sur l'existence de deux solutions.
Utilisation en classe - Ce texte très riche, dans lequel toutes les démonstrations sont soigneusement détaillées, permet une immersion dans les méthodes mathématiques mises en œuvre par les « Anciens », reprises et poursuivies ici par Newton, pour traiter certaines questions liées aux Sections Coniques. Certains passages de ce texte pourraient certainement être lus et commentés en classe préparatoire pour donner une perspective historique à l’étude des Coniques. Les professeurs de mathématiques du secondaire trouveront pour leurs élèves quelques situations de problèmes géométriques impliquant les rapports de longueurs, les angles, et bien sûr les triangles semblables. En particulier, le problème de Pappus dans le cas du cercle, qui fait l’objet de la Section 4, offre une configuration exploitable en classe de seconde. |
 |
Dossier
coordonné par Pierre
Crépel (CNRS)
Présentation - Pour vous, qui est D'Alembert ? - C'est l'Encyclopédie, mais moins que Diderot. C'est aussi un grand mathématicien du XVIIIe siècle, mais moins qu'Euler. Voilà, en ramassé, la réponse nue qui ressort d'un petit sondage auprès d'étudiants et d'un public divers cultivé mais non spécialisé. Elle n'est pas fausse. Sans Diderot, l'Encyclopédie n'aurait jamais possédé ce sel et ne serait pas allée jusqu'au bout; sans D'Alembert, elle n'aurait eu ni cette qualité scientifique, ni cet impact européen. Tout étudiant de mathématiques a travaillé, appliqué ou entendu évoquer le théorème de D'Alembert(-Gauss) ou théorème fondamental de l'algèbre, le principe de D'Alembert en mécanique, le paradoxe de D'Alembert en hydrodynamique, le critère de D'Alembert pour les séries, l'équation de D'Alembert pour les cordes vibrantes. Or, quand Condorcet, ami et disciple de D'Alembert, a lu successivement à l'Académie les éloges d'Euler et de D'Alembert, décédés à quelques semaines d'intervalle, les observateurs ont remarqué ceci: "On ne s'attendoit pas que Condorcet mettroit Euler si fort au dessus de d'Alembert, et le public lui en a su gré." Mais sait-on que D'Alembert a été secrétaire de l'Académie française et non de l'Académie des sciences ? sait-on que son principal correspondant est Voltaire, plus que Lagrange ? sait-on que la moitié de son oeuvre mathématique se situe après l'Encyclopédie alors qu'on dit qu'il n'en fait plus guère ? sait-on qu'il a écrit mille pages d'optique aujourd'hui oubliées ? Alors ? Grand géomètre aux dires des littérateurs et bon littérateur aux dires des géomètres? Les jugements de l'Histoire sont plus que contrastés et rarement un auteur, surtout scientifique, a suscité des avis aussi tranchés et aussi opposés. L'édition en cours de ses Oeuvres Complètes permet un regard nouveau. Plus que pour d'autres "génies de la science", ce dossier sera donc l'occasion de découvertes et d'imprévus, mais aussi de soutes, ce qui n'aurait pas déplu à ce savant des Lumières. |
| Par Jean-Philippe
Villeneuve, Cégep de Rimouski,
Rimouski,
Québec, Canada Résumé - Nous nous intéresserons aux premières théories de la mesure élaborées à la fin du 19e siècle et nous les utiliserons pour distinguer le processus d’abstraction du processus de généralisation. En effet, nous retrouvons des généralisations dans les versions calculatoires de la mesure proposées par Peano (1887), Jordan (1892) et Lebesgue (1902). En 1898, Borel présenta une nouvelle façon de définir la mesure : au lieu de la définir par un calcul, la notion doit satisfaire une liste de propriétés. Cette nouvelle façon de définir une notion implique un changement d’attention de la part de Borel et ce changement lui permettra de « reconstruire » la notion dans le sens où certaines propriétés des versions calculatoires deviennent constitutives de la nouvelle notion. De plus, cette reconstruction implique une réorganisation des connaissances mathématiques, comme l’intégration de connaissances jusqu’alors considérées comme distinctes. Nous obtiendrons ainsi que ce changement d’attention jumelé à la reconstruction et à la réorganisation des connaissances sont des caractéristiques du processus d’abstraction réfléchissante développé par Jean Piaget. Nous utiliserons de plus les recherches d’Aline Robert et de Jean Cavaillès pour éclairer notre analyse. Nous conclurons en remarquant que le processus d’abstraction change la compréhension de la notion, ce qui n’est pas nécessairement le cas pour une généralisation, et qu’il permet d’introduire les notions « spécialisées » que nous retrouvons dans la théorie contemporaine de la mesure. |
| Par Davide
Crippa, Equipe REHSEIS (CNRS et
Université Paris Diderot) Résumé -Le problème de la quadrature du cercle, à savoir, le problème de construire un carré ayant même aire que celle d'un cercle donné, restait un problème ouvert parmi les mathématiciens du début du XVIIème siècle. René Descartes (1596-1650) en donna une solution dans les années 1625-1628 dont il déclara lui-même qu'elle n'était pas acceptable. Cet article examine cette solution, en s'appuyant sur une analyse donnée un siècle plus tard par Euler ainsi que sur une solution connue depuis l'antiquité et rapportée par Pappus. On s'interrogera ensuite sur les raisons qui ont amené Descartes à exclure les deux constructions en tant que non acceptables, par rapport à l'idéal d'exactitude explicité dans La Géométrie (1637). Utilisation en classe – Une lecture commentée de certains passages de cet article peut certainement être envisagée dans une classe des cycles S ou L (option « maths »). La seconde partie offre une ressource qu’il serait possible d’utiliser comme base pour une activité faisant intervenir la somme des termes d’une suite géométrique, ceci autour d’une configuration géométrique visant à rechercher une solution au problème de la quadrature du cercle. La discussion de la troisième partie concernant la recevabilité et l’exactitude de la construction géométrique d’une courbe offre un thème qui pourrait faire l’objet d’un travail interdisciplinaire entre mathématiques et philosophie. |
Autre Ressource sur CultureMATH
Ressources externes
| Par Lény
Oumraou, Docteur
agrégé de philosophie
- Lycée Charles Péguy (Orléans) et
Université Paris I Résumé - Alan Turing (1912-1954) est, à juste titre, considéré comme le co-inventeur de l'ordinateur (avec J. von Neumann). La « machine de Turing universelle » est bien une préfiguration théorique du « calculateur programmable ». Dans ses travaux fondateurs de 1936, Turing se référaient directement à des questions de calculabilité (les nombres réels calculables) et de décidabilité (le problème de la décision, ou Entscheidungsproblem de Hilbert). Dans l'article de 54, c'est en partant de considérations moins « confidentielles », destinées à un plus large public, qu'il présente une (petite) partie de la théorie de la calculabilité. Les « puzzles » (casse-têtes, énigmes, etc.) forment le point de départ de la discussion. Partant de ces « récréations mathématiques », Turing expose une nouvelle formalisation des algorithmes, dans l'esprit des travaux plus récents de Post et Markov. Utilisation en classe - Parmi les « puzzles » étudiés dans le texte, une place importante est donnée au taquin. En suivant la démarche de Turing, on peut envisager un examen approfondi, et non moins ludique, de ce jeu, qui fournit une intéressante application de la théorie des groupes ; on peut même considérer des versions simplifiées (3×3 cases au lieu de 4×4), ou au contraire d'une plus grande complexité, dans une approche combinatoire (méthode de partition). Il peut également illustrer des questions d'algorithmique générale (par exemple les différentes manières d'explorer un arbre) et sensibiliser aux problèmes de la théorie élémentaire de la calculabilité (notion de procédure effective, de complexité algorithmique, etc.). |
| Par Marc
Chemillier, Directeur
d'études à l'École des Hautes
Études en Sciences Sociales (EHESS) Résumé - Dans la tradition musicale savante occidentale (et cela vaut aussi pour les traditions savantes non occidentales comme la tradition chinoise), la musique a toujours été associée aux mathématiques. Dans le contexte de sociétés sans écriture, en revanche, cette association peut paraître plus surprenante. Le but de cet article est de montrer quelques cas de répertoires musicaux de tradition orale dans lesquels on peut mettre en évidence des structures musicales complexes comparables à des constructions mathématiques. |
|
Par Jean-Philippe Villeneuve, Cégep de Rimouski, Rimouski, Québec, Canada Résumé - Nous retrouvons au 19e siècle quatre façons de définir ou de comprendre la notion mathématique d’intégrale : l’intégrale de Cauchy, l’intégrale de Riemann et les versions calculatoire et axiomatique de l’intégrale de Lebesgue. Nous proposons d’étudier les généralisations de ces façons de définir l’intégrale en introduisant deux types de généralisations : les généralisations conservatives et les généralisations innovantes. Dans le premier cas, la façon de définir l’intégrale ou de calculer l’intégrale est conservée et son extension est augmentée, c’est-à-dire qu’il y a plus de fonctions qui sont intégrables selon cette façon. Dans ce second cas, la façon de comprendre l’intégrale change et il y a une réinterprétation, voire une reconstruction de la notion. Utilisation
en classe
- Les enseignants de mathématiques trouveront dans cette
approche historique et épistémologique de la
notion
d’intégrale des éléments
pour enrichir
l’introduction historique de cette notion faite aux
élèves de terminale.
Pour les classes Post-Bac, dans lesquelles l’intégrale de Riemann est approfondie, une lecture accompagnée et commentée montrerait aux élèves que la notion d’intégrale a traversé le 19e siècle d’une façon dont on peut rendre compte grâce à quelques outils conceptuels. |
|
Par Anne-Marie Décaillot, Equipe REHSEIS (CNRS, Université Paris-Diderot) Résumé - Franz Goldscheider (1852-1926) est un « ancien élève » de Cantor, professeur de mathématiques dans un lycée de Berlin. La lettre de Cantor du 18 juin 1886, dont nous donnons ci-dessous une traduction française, est la première manifestation connue d’un échange entre les deux mathématiciens, qui se poursuivra de 1886 à 1888. Cette première lettre constitue un véritable exposé introductif des fondements de la théorie cantorienne des ensembles, présentant les notions de cardinaux et d'ordinaux et leurs premières manipulations opératoires. La lettre expose, avec de nombreux exemples imagés à l’appui, les notions d’équivalence et de puissance ensemblistes ; puis l’arithmétique des nombres cardinaux met l’accent sur les spécificités opératoires concernant les nombres transfinis. La notion d’ensemble bien ordonné est alors définie, ainsi que celle cruciale de nombre ordinal et d’ensembles conformes. De nombreux exemples permettent d’éclairer les règles de calcul régissant les nombres ordinaux transfinis. Cantor parvient ainsi à la définition du nombre ordinal ω (nombre ordinal de l’ensemble des entiers ordonnés dans l’ordre naturel) et de la puissance ω* (nombre cardinal de l’ensemble des entiers). La deuxième classe de nombres apparaît alors comme l’ensemble de tous les nombres ordinaux, qui sont des types d’ensembles bien ordonnés de puissance ω*. Il y a autant de nombres ordinaux de deuxième classe que de relations de bon ordre sur l’ensemble des entiers. La lettre que nous
éditons
ici en langue française prouve une fois encore l'importance
des correspondances dans la formation d'une pensée
mathématique et permet de reconstituer la genèse
du
dernier grand mémoire de théorie des ensembles,
les Beiträge,
publié entre 1895 et 1897 par Georg Cantor, où
ces
notions seront publiées et approfondies.
|
|
Les Annales de Gergonne (1810-1832) et le Journal de Liouville (1836-1845), par Christian Gerini (Université de Toulon) & Norbert Verdier (Université Paris-Sud). Résumé : Les mathématiques ont bénéficié, dans la France et l’Europe du XIXème siècle, d’une nouvelle forme de communication : les périodiques qui leur ont été dédiés. Les Annales de Joseph-Diez Gergonne, publiées mensuellement de 1810 à 1832, constituent le premier journal de mathématiques. Joseph Liouville, en digne successeur de Gergonne, publia à partir de 1836, sous une forme héritée des Annales, le Journal de Mathématiques Pures et Appliquées. Nous nous intéressons ici à ces deux périodiques sous un angle transdisciplinaire : histoire de la diffusion scientifique en les situant par rapport à d'autres journaux de cette première moitié du XIXème siècle, histoire des mathématiques, épistémologie. Il s’agit de porter à la connaissance de la communauté des mathématiciens et des historiens des sciences des documents originaux riches d’enseignements sur la construction des concepts et théories. Ces textes sont progressivement mis à la disposition d’un public élargi via les nouveaux modes de communication et d’archivage. L’histoire de leur genèse, de leurs contenus et de leurs auteurs est de ce fait à nouveau d’actualité. Cet article
s’appuie en
grande partie sur la publication suivante :
« Les Annales de Gergonne
(1810-1832) et le Journal de Liouville
(1836-1874) : une mine de textes numérisés
à
exploiter dans notre enseignement. », Christian
Gérini & Norbert Verdier, Repères,
67, 55-68, Topiques éditions, 2007. Nous remercions vivement
Yves Ducel d’avoir
autorisé cette reprise sous forme
électronique.
Utilisation en classe - Les lecteurs de cet article seront frappés par l'importance de la contribution des lycéens et étudiants et de leurs professeurs aux premiers périodiques mathématiques, ainsi que par le rôle qu'y jouent l'élaboration et la résolution de problèmes. Les Annales de Gergonne et le Journal de Liouville offrent ainsi des ressources inépuisables pour l'enseignement. On trouvera en annexe de l'article les "Questions du Dimanche" de Norbert Verdier, une liste de problèmes publiés dans les périodiques et ouvrages mathématiques du XIXe siècles soumis à la sagacité des lecteurs de CultureMATH. |
  |
|
 |
|
Autres ressources sur CultureMath
Ressources externes pour en savoir plus sur l'Arbre de Stern-Brocot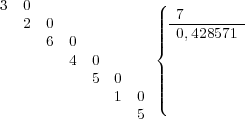 |
|
Résumé - Bien des approches de la géométrie grecque ancienne sont possibles. Les grands textes des auteurs hellénistiques, notamment certains fameux problèmes tels que la quadrature du cercle ou la duplication du cube, ont joué un rôle indéniable dans l’histoire des mathématiques jusqu’à une date récente et ont intéressé — et intéressent toujours — les historiens des sciences, les enseignants, le public cultivé … Plusieurs questions restent cependant sans réponse : les premières recherches mathématiques des Grecs nous échappent en grande partie ; nous ignorons à peu près tout de la biographie (en particulier intellectuelle) des principaux géomètres ; les modalités de l’enseignement des mathématiques dans l’Antiquité nous sont fort mal connues. Bien que lacunaires, les sources ne sont pourtant pas muettes. Des oeuvres mathématiques majeures sont parvenues jusqu'à nous au terme de processus de transmission complexes, en particulier par le biais de la tradition savante écrite en langue arabe. Dans ce dossier, Bernard Vitrac présente les oeuvres d'Hippocrate, Euclide, Archimède, Apollonius, Ptolémée, Héron, Ménélaos..., et évoque des lieux et des contextes historiques particulièrement importants pour l'histoire des mathématiques (les cités ioniennes, Athènes, Alexandrie...). Le dossier se répartit en dix articles, complétés par des outils annexes qui seront utiles aux enseignants : bibliographie, chronologie, carte, ainsi qu'une liste des oeuvres mathématiques grecques parvenues jusqu'à nous.
Utilisation en classe - En insistant sur le contexte historique et intellectuel du développement des mathématiques en Grèce ancienne, ce dossier intéressera aussi bien les enseignants de mathématiques que ceux d'histoire, de lettres ou de philosophie. Par leur style clair et accessible, les textes s'adressent aussi à un public de lycéens, notamment à ceux qui voudraient s'engager dans des travaux personnels encadrés en histoire des mathématiques. Des encarts contenant des démonstrations mathématiques détaillées peuvent être exploités en classe au niveau du collège ou au niveau du lycée.
Autres ressources sur CultureMath
 |
|
|
Préface du livre, par Eric Van der Oord, Inspecteur général de l’Education nationale
Denis Favennec et Emmanuel Riboulet-Deyris enseignent les mathématiques en classes préparatoires aux grandes écoles. En bons mathématiciens, ils savent bien que les théories qu’ils enseignent, les définitions, les théorèmes, ces belles routes tracées pour la pensée des hommes, sont toujours construites sur un ensemble de sentiers longuement parcourus par des chercheurs aux pas parfois incertains.
Dans cet ouvrage, ils nous invitent à découvrir les chemins parcourus par l’esprit humain entre la découverte de la perspective en peinture et l’invention de la géométrie projective en mathématiques.
Pour mesurer l’étendue de la
période
étudiée, il suffit de comparer deux
séries de
dates :
1415 Invention de la perspective par Brunelleschi
1435 Alberti publie son De pictura
1482 Piero della Francesca publie son De
prospectiva pingendi
1543 Publication de De revolutionibus orbium
caelestium de Copernic
1616 Condamnation de Copernic
1633 Condamnation de Galilée
1639 Invention de la géométrie projective par
Desargues
1687 Publication des Principia mathematica de
Newton
Que s’est-il passé durant ces deux siècles ?
C’est ce que se proposent de montrer les auteurs. Ils feront voyager le lecteur dans un monde où l’espace de la physique mathématique et de la géométrie, familier pour les bacheliers d’aujourd’hui, n’est pas encore inventé. Un monde où, selon les conceptions d’ Aristote , un objet ne peut être considéré que dans un certain domaine, et où ses propriétés ne relèvent pas de lois universelles mais des lois de son domaine — par exemple les corps terrestres se déplacent en ligne droite, mais les corps célestes décrivent des cercles. Un monde où, en géométrie, on admet qu’un segment puisse être prolongé autant que nécessaire, mais où la droite n’est pas conçue dans sa globalité. Un monde enfin où l’infini « actuel » étant une prérogative divine, son apparition dans un tableau pourrait être considérée comme sacrilège, et où le peintre peut être tenté de cacher les points de fuite de ses perspectives. Dans ce monde, une pléiade d’artistes ont utilisé la perspective pour construire leurs tableaux, tant pour donner au sujet représenté des proportions harmonieuses que pour orienter le regard du spectateur sur l’essentiel. En examinant les nombreux tableaux commentés dans l’ouvrage, le lecteur découvrira sans cesse, selon une expression de Daniel Arasse , « cette géométrie secrète de l’oeuvre peinte qui, en tout temps, a été pour les artistes une des composantes essentielles de la beauté » . Au terme de cet itinéraire passionnant, le lecteur aura constaté, pour reprendre une phrase de l’ouvrage, que la fin assignée à la perspective, aussi bien par la théorie que par la pratique, est la production d’un sens plutôt que d’une illusion .
Utilisation en classe - Cet article, ainsi que la lecture à laquelle il convie, enrichit le dossier de CultureMath sur l'histoire de la perspective. Tout comme l'article sur le mathématicien J.-H. Lambert (1728-1777), il aborde les relations étroites de la géométrie avec l'histoire de l'art, un sujet particulièrement intéressant pour les sections littéraires.
Autres ressources sur CultureMath
|
Résumé - ‘Les écritures mayas du nombre’ sont une synthèse des plus récents résultats d’analyses épigraphiques et linguistiques du corpus des écritures numérales et numériques réalisées par les scribes mayas depuis l’époque préclassique jusqu’à celle de la conquête espagnole. Interprétées dans le cadre des numérations parlées (de types protractif et additif) et dans celui des mesures de temps, la grande diversité des données analysées conduit à une typologie de l’ensemble des formes (notamment des zéros) et des systèmes mayas d’écriture du nombre, tant dans la représentation des dates et des petites durées, que dans celle des translations temporelles et des grandes durées. Diverses remarques présentent et discutent des usages spécifiques (âge de la Lune, durée d’une lunaison, pas de translation dans les almanachs divinatoires), des interprétations (zéro comme signe d’achèvement, d’intronisation, etc.), des distinctions marquées par les scribes (ordinal/cardinal, prospectif/ rétrospectif), ou encore des thèses alternatives (unité principale du système des mesures de temps, hypothèse courte, zéro opérateur).
Utilisation en classe - Cet article intéressera les enseignants désireux d'accéder à une réflexion approfondie sur les problèmes historiques, philologiques et linguistiques que pose la compréhension des systèmes numériques anciens. Pour trouver une documentation adaptée à l'enseignement dans les classes de collège et de lycée, ils pourront se reporter au dossier "Les numérations anciennes" et en particulier à la fiche pédagogique "Nombres mayas".
Autres ressources sur CultureMath
|
Consulter le dossier |
|
Utilisation en classe - Les 15 problèmes de Jean-Henri Lambert sont des constructions à la règle seule qui peuvent être exploitées à tous les niveaux de l'enseignement secondaire. Certains sont bien connus des enseignants, comme le problème V (deux droites D et D' se coupent hors de la feuille; sans les prolonger, construire une droite concourante avec D et D' et passant un point donné). Ces problèmes anciens prennent un intérêt renouvelé dans le cadre des nouveaux programmes de mathématiques des sections littéraires, qui désormais abordent la perspective centrale:
La problématique de la représentation de l’espace en fonction des finalités visées, artistiques ou techniques, conduit d'une part à mettre en oeuvre les connaissances géométriques, dans l'espace mais aussi dans le plan, et d'autre part à aborder des questions de nature culturelle et artistique. (p. 1) [...] Grâce au programme de l’option de première, les élèves [de terminale] disposent désormais à la fois de résultats de géométrie dans l’espace et d’un outil de visualisation des configurations, la perspective parallèle. Il s’agit maintenant d’étudier les rudiments de la perspective centrale, mode géométrique de représentation de l’espace qui a constitué, durant plusieurs siècles, le principe de la réalisation des oeuvres d’art pictural en Occident. (p. 5)
Par ses relations étroites avec l'histoire de l'art, l'histoire de la perspective est un sujet d'étude particulièrement intéressant à aborder dans les sections littéraires.
Autres ressources sur CultureMath
|
|
|
Utilisation en classe – Ce diaporama a été élaboré en Terminale scientifique à la demande conjointe d’Élisabeth ARBOGAST, professeur de mathématiques et Nafissa HAIDAR, professeur de philosophie, toutes deux au lycée Ribeaupierre de Ribeauvillé (Haut-Rhin). Au départ, Mme Haidar avait souhaité un exposé sur la géométrie non euclidienne et à partir de là, aborder les questions d’épistémologie au programme de la classe de Terminale Scientifique. Très vite, nous nous sommes mis d’accord sur l’objectif suivant : mettre en mouvement une dynamique de réflexion qui rompe avec le cloisonnement disciplinaire, et qui amène les élèves à se dire lorsqu’ils font des mathématiques : quel est le sens de ce que je fais en mathématiques ? En quoi est-ce une science exacte ? Comment s’est–elle construite ? Quel lien avec ce que je fais en philosophie ? Et lorsqu’ils sont en cours de philosophie : quels exemples puis-je tirer de mes autres apprentissages, mathématiques, physique, SVT, etc. pour donner corps aux concepts philosophiques, pour illustrer des thèmes comme intuition, évidence, vérité, rigueur, imagination, réalité ?
Ressources externes
|
|
Ressources sur CultureMath
Ressources externes
A lire
 |
|
Cet article aborde, en l'inscrivant dans une réflexion historique, une question que se pose en permanence l'institution scolaire, et que l'actualité vient de remettre au premier plan, pour ce qui est de l'élémentaire, avec la publication de l'Avis de l'Académie des Sciences sur la place du calcul dans l'enseignement primaire (voir le point de vue d'historien de Renaud d'Enfert sur cet avis, diffusé par le site EducMath)
Pour mesurer l'intérêt de ce regard vers le passé, citons la conclusion: "Ce parcours partiel et trop rapide des principes qui ont guidé les orientations de différents programmes de géométrie depuis un siècle et demi illustre bien la diversité des enjeux à l’œuvre dans l’enseignement des mathématiques. Celui-ci se trouve en effet au carrefour de contraintes d’ordre disciplinaire, épistémologique, social, idéologique, pédagogique dont la résultante a dépendu des temps et des publics concernés. Les perspectives pour l’enseignement des mathématiques pour ce siècle sont ainsi à réfléchir en fonction de l’état des mathématiques, du rôle qu’elles jouent aujourd’hui dans la société et des ambitions affichées pour l’école."
Autres ressources de CultureMath sur l'histoire de l'enseignement
Ressources externes
Du côté de l'actualité
Voir l'Avis de l'Académie des Sciences sur la place du calcul dans l'enseignement primaire, adopté le 9 janvier 2007, et les premières réactions sur EducMath (commentaires de Guy Brousseau, Catherine Houdement, Jean-Pierre Kahane, Michèle Artigue, Roland Charnay, Jean-Pierre Demailly, Renaud d'Enfert ...).
A lire
Dans «Les Génies de la science», N° 31 mai 2007
- L’enseignement du calcul à l’école primaire par Renaud d’Enfert
- Les sciences au lycée : l’avis des savants par Hélène Gispert
|
|
|
De même que, dans les mathématiques contemporaines, les matrices sont susceptibles de représenter une diversité d’objets algébriques, leur histoire se joue sur une longue période, dans des contextes divers et s’enrichit de la rencontre entre différents champs de recherche. Dans cet article nous rentrons dans le détail de textes publiés entre 1850 et 1890 par des auteurs comme Arthur Cayley, James Joseph Sylvester et Eduard Weyr. En mettant un avant les contextes culturels dans lesquels s'inscrivent ces différents auteurs, nous observerons des pratiques différentes dont la rencontre provoquera un enrichissement du champ des significations associées à la notion de matrice. Nous verrons que poser la question de l'histoire de la notion de matrice permet d'observer des aspects culturels des mathématiques antérieurs aux théories structurelles et unificatrices comme l'algèbre linéaire des années trente du XXe siècle.
Cet article s'appuie sur de nombreux extraits de textes originaux placés dans le corps du texte et sous forme d'encarts, la lecture n'en est cependant jamais obligatoire et l'ensemble de l'article peut être parcouru en laissant à une seconde lecture l'étude des citations.
Plusieurs problèmes mathématiques présentés dans cet article peuvent être abordés avec des étudiants. Selon le niveau de généralité choisi (matrices symétriques, diagonalisables ou quelconques, à coefficient dans un corps algébriquement clos ou dans un anneau principal) les problèmes proposés peuvent être exploités à des niveaux très différents, des premières années d'université à la préparation de l'agrégation.
Le problème des types d'intersections des coniques étudié par Sylvester entre 1850 et 1851 peut donner lieu à un travail sur les difficultés posées par la multiplicitédes valeurs propres d'une matrice. Les différents types d'intersections de coniques permettent de représenter dans un cadre géométrique les différentes décompositions du polynôme caractéristique ou minimal et les différentes formes canoniques associées.
Le problème de la détermination des "racines" des fonctions homographiques posé par Cayley en 1858 fournit une situation dont l'étude peut déboucher, de manière constructive, à l'introduction des "lois" du calcul matriciel et des pratiques polynomiales associées (théorème de Cayley-Hamilton). Le problème des matrices périodiques permet d'aborder les difficultés propres au calcul matriciel (anneau non intègre et non commutatif). L'ambigüité de la notion de "single quantity" de Cayley et l'efficacité des pratiques polynomiales qui l'accompagnent peuvent donner lieu à un travail sur les quantités multiples (algèbres associatives).
Les travaux menés par Sylvester entre 1880 et 1885 permettent de travailler sur le problème de la définition des fonctions de matrices. Un travail peut également être mené sur les quaternions et les nonions afin d'introduire les méthodes élaborées pour la détermination des matrices qui commutent avec une matrice donnée (polynôme minimal, matrices dérogatoires, nullité d'une matrice).
Les procédés opératoires sur la forme matricielle élaborés par Eduard Weyr entre 1885 et 1890 permettent d'introduire ou d'approfondir la principale méthode de démonstration du théorème de Jordan (décomposition de l'espace en sous espaces caractéristiques invariants pour un opérateur donné).
Enfin, la présentation, dans la première partie de cet article, de la synthèse théorique élaborée dans les années trente permet de mettre en évidence les enjeux pédagogiques portés par la forme matricielle. En même temps que s'élabore une synthèse qui donne à la théorie des matrices un caractère universel, les traités des années 1930 adoptent une organisation didactique basée sur le caractère opératoire de la représentation imagée des matrices, représentation présentée comme simple, efficace et permettant d'assimiler des théorèmes généraux.
|
Agathe Keller, équipe REHSEIS (CNRS et Université Paris 7)
|
Résumé – La tradition savante indienne est traversée par un paradoxe : une abondance de manuscrits témoigne de textes qui privilégient une transmission orale du savoir. Il en va ainsi pour les mathématiques, comme pour d’autres disciplines savantes. Cette prééminence de l’oralité comme valeur de transmission du savoir, a-t-elle eu une influence sur la manière dont on a pratiqué les mathématiques en Inde? Pour répondre à cette question, l'auteur nous entraîne dans l'aventure des manuscrits au travers de la tradition védique et de la culture sanskrite.
Utilisation en classe – Les enseignants trouveront dans cet article des énoncés de problèmes stimulants pour tous les niveaux de l'enseignement secondaire (de la proportionnalité à la théorie des nombres).
Ressources sur CultureMath
Ressources sur le site de l'IUFM de la Réunion
 |
|
Résumé – L’architecture créole réunionnaise recourt abondamment à des motifs géométriques. Les lambroquins, ces frises de bois ou de tôle qui bordent les toitures, en constituent l’un des éléments les plus caractéristiques. Dans ce dossier, on se propose de présenter l’origine, la fonction utilitaire et la fonction décorative des lambroquins, d’étudier plus spécifiquement leur structure géométrique et de les situer par rapport à l’ensemble des dessins à motifs répétitifs employés dans l’art et l’architecture. Les cinq types de lambroquins rencontrés à la Réunion, leurs fréquences d’emploi et leurs enrichissements esthétiques constituent une véritable signature ethnomathématique de la culture créole insulaire qui s’est développée dans ce département français de l’océan Indien.
Utilisation en classe – À la Réunion, les lambroquins offrent un support naturellement pertinent pour enrichir l’enseignement des mathématiques en s’appuyant sur le vécu culturel des enfants. On évoque ici plusieurs expériences pédagogiques réalisées dans des collèges et des lycées de l’île, en souhaitant que les enseignants d’ailleurs puissent également s’en inspirer.
Ressources sur CultureMath
Ressources externes
A lire
|
Maryvonne Spiesser (maître de Conférence à l'Université de Toulouse III). Cet article a été publié dans le Bulletin de l’APMEP n°444, 2003, p. 32-50. Le texte diffusé par CultureMATH est la version intégrale, avec quelques corrections mineures. Il est mis en ligne sur CultureMATH avec l'autorisation de l'APMEP, que nous remercions chaleureusement. |
Résumé - Au cours du XVe siècle, un nouveau type de traités d’arithmétique pratique se développe en France en dehors de l’Université. Ce sont des ouvrages pédagogiques, qui reflètent la nécessité d’une formation mathématique pour les futurs marchands, formation dont on connaît très peu les modalités. En dehors de l’apprentissage du calcul, l’apprenti marchand apprend à gérer mathématiquement des situations qu’il rencontrera au quotidien, toutes régies par la règle de trois ; il se mesure aussi à des exercices plus plaisants, qui complètent sa formation. Les méthodes d’apprentissage sont fondées sur l’application de règles, présentées de manière algorithmique et accompagnées de nombreux exemples d’entraînement. Cet article en présente un certain nombre, pour la plupart très répandus dans ce type d’ouvrages. Le courant des « arithmétiques commerciales » puise ses sources dans un passé souvent lointain ; et sans toutefois demeurer créateur, il va perdurer jusque dans la première partie du XXe siècle, à travers les manuels d’arithmétique de l’école élémentaire.
Utilisation en classe - Cet article fournit un riche matériau pour des activités en classe. En effet, les nombreux exemples sont une source d’énoncés permettant de mettre en pratique des notions mathématiques essentielles comme la proportionnalité. Par ailleurs, la formation mathématique des marchands dans l'Europe de la Renaissance est un sujet intéressant à exploiter dans le cadre d'un travail interdisciplinaire : le thème des énoncés de problème montre une production mathématique en liaison étroite avec la vie sociale, ici le négoce. Grâce à cette documentation, les professeurs d'histoire pourront notamment montrer comment la tradition commerciale a contribué à préserver et à diffuser un patrimoine qui s’est enrichi et qui a évolué au cours des temps et au contact de différentes civilisations. Enfin, les enseignants et les formateurs trouveront dans ces problèmes pratiques matière à réflexion sur la forme de l’exposé mathématique et les modes de justification, adaptés aux objectifs et au lectorat, dépendant aussi des traditions et des outils mathématiques dont on dispose.
importer l'article en version pdf
Ressources sur CultureMath
Ressources externes
|
|
|
Ressources sur CultureMath
Les mathématiques et l’enseignement féminin en France, Nicole Hulin, 2006 (publié dans le Bulletin de l’Union des professeurs de Spéciales, n°197, janvier 2002, p. 12-17).
De l’Association des professeurs de mathématiques (APM), Nicole Hulin, 2006.
Pourquoi, pour qui enseigner les mathématiques? , Hélène Gispert, 2007 (publié dans le Bulletin de l'APMEP n° 438 en janvier 2002).
Ressources externes
L’enseignement mathématique à l’école primaire de la Troisième République aux années 1960: enjeux sociaux et culturels d’une scolarisation «de masse», Renaud d'Enfert, 2006.
L’enseignement du travail manuel dans les écoles primaires de garçons: Travaux d’élèves de l’école Louis Vauquelin de Rouen, 1886-1887, Renaud D'Enfert, 2007
L’enseignement des mathématiques dans ses liens à d’autres disciplines, une perspective historique, Hélène Gispert et Nicole Hulin, article paru dans le bulletin de l'Union des Professeurs de Spéciales, n°192, octobre 2000.
Les exercices pratiques de mathématiques dans l’enseignement secondaire, Conférence faite le 3 mars 1904 au musée pédagogique par Emile Borel (avec une présentation de Hélène Gispert), Gazette de la SMF.
Femmes et mathématiques dans le monde occidental, Renate Tobies, Gazette de la SMF.
Avis de l'Académie des Sciences sur la place du calcul dans l'enseignement primaire de janvier 2007 et dossier sur le site EducMath (voir notamment un point de vue historique par Renaud d'Enfert).
A lire
Le dessin à l'école de 1800 à nos jours, Renaud D'Enfert, Daniel Lagoutte, Lyon, INRP, 2004.
L’introduction du travail manuel dans les écoles primaires de garçons, 1880-1900, Renaud D'Enfert, Histoire de l’éducation, n° 113, janvier 2007, pp. 31-67.
L'enseignement mathématique à l'école primaire, de la Révolution à nos jours. Textes officiels réunis et présentés par Renaud d'Enfert, avec la collaboration d'Hélène Gispert et de Josiane Hélayel. Tome 1 : 1791-1914. Paris, INRP, 2003.
Dans «Les Génies de la science», N° 31 mai 2007:
- L’enseignement du calcul à l’école primaire par Renaud d’Enfert.
- Les sciences au lycée : l’avis des savants par Hélène Gispert.
 |
|
Introduction - Tout le monde sait distinguer premier, second et dernier, ou encore un, deux et beaucoup. Mais comment construire le nombre abstrait, c’est-à-dire développer et articuler entre elles : la capacité « ordinale » de distinguer des entités sur la seule base de leur rang dans une suite, et la capacité « cardinale » de déterminer des quantités hétéroclites par la seule propriété d’avoir le même nombre d’éléments ou d’être de même mesure ? On comprend qu’il s’agit d’une longue aventure humaine collective en observant comment s’écrivent les grands nombres dans différentes parties du monde.
Utilisation en classe - Cet article apporte des matériaux pour les enseignants et les élèves des sections littéraires qui, avec les programmes de 2004, découvrent une nouvelle manière d’aborder l’arithmétique : « L’étude de différents systèmes de numération historiques et actuels se révèle fructueuse tant sur le plan de l’histoire des cultures que sur le plan mathématique. Cette étude permet de revenir sur la distinction entre un objet et sa désignation (ici, nombre et écriture chiffrée), sur la distinction entre les propriétés intrinsèques des entiers naturels et celles liées aux systèmes de numération (ici divisibilité et critères de divisibilité). Elle permet un retour réflexif sur les mécanismes sous-jacents aux techniques opératoires, dont l’aspect algorithmique doit être mis en valeur. » (Programmes des lycées, mathématiques, classe de première, série littéraire, BO hors série n°5, 9 sept. 2004).
Ressources sur CultureMath
Ressources externes
Un article de Nicole Hulin, maître de conférences honoraire à l’Université Pierre-et-Marie-Curie - Paris VI, chercheur au Centre Alexandre Koyré.
Résumé - L’APMEP (association des professeurs de mathématiques de l'enseignement public) est l’une des associations de spécialistes, constituées pour accompagner les professeurs du secondaire dans l’application de la réforme majeure de 1902. Son premier Bulletin de liaison est publié en 1911. Une dizaine d’années plus tard l’APMEP va se mobiliser pour dénoncer le caractère néfaste pour l’enseignement des sciences de la réforme dite de « l’égalité scientifique » et demander le retour aux principes de 1902.
lire l'article - importer l'article en fichier pdf
Ressources sur CultureMath
Ressources externes
A lire
Dans «Les Génies de la science», N° 31 mai 2007
- L’enseignement du calcul à l’école primaire par Renaud d’Enfert
- Les sciences au lycée : l’avis des savants par Hélène Gispert
 |
|
Utilisation en classe - Cet article intéressera tout autant les professeurs de mathématiques que les professeurs d'histoire, qui y trouveront des idées d'activités interdisciplinaires pour leurs élèves. Par exemple, les calculs des marchands assyriens (conversions de la valeur des marchandises en quantités d'or, d'argent ou de grain), peuvent apporter tout à la fois des exercices d'application de la proportionnalité au collège, et une façon originale de découvrir le commerce à longue distance il y a 4000 ans. Dans le cadre de la présentation des numérations anciennes en première littéraire, on pourra s'intéresser au curieux mélange de numération sexagésimale d'origine sumérienne et de numération décimale que pratiquaient les populations du nord de la Mésopotamie.
Ressources sur CultureMath
Les mathématiques et l’enseignement féminin en France. Quelques jalons pour un siècle d’histoire, Nicole Hulin (article publié dans le Bulletin de l’Union des professeurs de Spéciales, n°197, janvier 2002, p. 12-17).
L'auteur est ancienne élève de l’ENS (Sèvres). Elle est aujourd’hui maître de conférences honoraire à l’Université Pierre-et-Marie-Curie - Paris VI, chercheur au Centre Alexandre Koyré. Elle est par ailleurs titulaire d’une agrégation scientifique « masculine » (par dérogation spéciale).
Résumé - En un siècle l’enseignement féminin est passé d’une organisation spécifique à la fusion avec l’enseignement masculin. Nous nous proposons d’indiquer ici quelques étapes de cette évolution, en centrant notre intérêt sur la partie scientifique de l’enseignement et plus particulièrement les mathématiques, tant au niveau secondaire qu’à celui du recrutement des professeurs avec l’agrégation.
Ressources sur CultureMath
Ressources externes
A lire
Dans «Les Génies de la science», N° 31 mai 2007
- L’enseignement du calcul à l’école primaire par Renaud d’Enfert
- Les sciences au lycée : l’avis des savants par Hélène Gispert
 |
|
Résumé
- Le Compendy de la practique des nombres est
un traité d’arithmétique
écrit à la fin du XV° siècle
à Lyon par un
Frère Dominicain, Barthélemy de Romans. Le
manuscrit est aujourd’hui
conservé à la Bibliothèque
Malatestiana de Cesena en Romagne (Italie).
Après un bref exposé du calcul écrit
utilisant la numération
indo-arabe, qui se répand à cette
époque dans les milieux marchands en
Europe du sud (numération positionnelle,
opérations sur les entiers et
les fractions, calcul approché de racines carrées
ou cubiques), la
majeure partie de l'ouvrage est consacrée à la
résolution
très approfondie de quelques types de problèmes
linéaires. Il témoigne
d’une volonté enseignante forte de la part de son
auteur, notamment en
direction de la formation des marchands. Mais son style montre aussi
des ambitions scientifiques inhabituelles. Le traité
présente en fait
peu d'intérêt pour un marchand : la
première partie est trop réduite
pour apporter l’essentiel et la seconde est inutile
à la pratique
commerciale. S’il fallait le rebaptiser, on pourrait le
qualifier
d’essai, un essai sur quatre problèmes,
destiné à illuminer
l’entendement de ceulx qui vouldroient veoir les subtilitez
qui y sont contenues ».
Utilisation en classe - Les enseignants de collège et de lycée trouveront dans cet article, et plus généralement dans le très riche corpus des arithmétiques marchandes, de nombreuses idées de problèmes linéaires qui illustrent la vie sociale dans l'Europe méditerranéenne à la Renaissance.
Lire l'article en version html ou importer l'article en version pdf
Ressources sur CultureMath
Ressources externes
Pour aller plus loin, on peut se reporter à l'édition critique du manuscrit complet par l'auteur: "Une arithmétique commerciale du XVe siècle: le Compendy de la practique des nombres de Barthélemy de Romans." Turnhout, Brepols, Coll. de Travaux de l'Académie internationale d'histoire des sciences, série De diversis artibus. 762 p.
 |
|
Résumé - C’est entre 1664 et1666, alors que Newton n’a pas encore 25 ans, qu’il jette les bases du calcul des « fluxions », c’est-à-dire de ce que nous appelons aujourd’hui les dérivées. Il s’agit donc d’un acte fondateur de l’analyse comme branche des mathématiques. Les deux premières années de recherche d'Isaac Newton furent probablement les plus fructueuses de sa vie de mathématicien.
Marco Panza nous présente un « très mauvais étudiant dans une très mauvaise université », peu soutenu par sa famille. Mais le jeune Isaac n’est pas un « mauvais étudiant quelconque dans une mauvaise université quelconque » : il se livre à la lecture de deux œuvres mathématiques novatrices : l’Arithmetica Infinitorum de John Wallis et la Géométrie de René Descartes. La culture mathématique du jeune Newton est donc tout à fait sélective. Son génie est d’avoir reconnu que le problème traité par Wallis, les quadratures, n’est autre que le problème réciproque de celui qui est traité par Descartes, les tangentes : « Newton se rend compte d’une chose étonnante : l’algorithme de Hudde [utilisé par Descartes pour trouver les tangentes], qui apparemment s’appliquait à un problème totalement différent de celui de Wallis pour trouver les aires, est en fait le même algorithme, mais inversé. Si je prends l’algorithme pour trouver les tangentes et je l’inverse, je trouve les aires ; si je prends l’algorithme pour trouver les aires et je l’inverse, je trouve les tangentes. Pour Newton, cela ne peut pas être un hasard, il doit y avoir quelque chose de profond. Newton veut trouver une théorie pour exprimer ce phénomène, il veut trouver un objet mathématique qui contient dans son comportement cette réciprocité. Cet objet est celui qui deviendra par la suite le calcul des fluxions, c’est-à-dire un des fondements du calcul infinitésimal et de l’analyse ».
Sommaire des vidéos:
1- Pourquoi un livre sur Newton
2- Le petit Isaac
3- Newton autodidacte
4- La lecture de Descartes
5- La lecture de Wallis. Le calcul des fluxions
6- La place des mathématiques dans l’œuvre de NewtonVoir les vidéos
(pour un meilleur affichage, nous conseillons d'ouvrir cette page en passant par le navigateur Mozilla)Documents d'accompagnement
1- La vie et l’œuvre d’Isaac Newton : repères chronologiques
2- Extraits de livre
Deux ouvrages viennent d’être publiés par Marco Panza : Isaac Newton , Les Belles Lettres, Paris (2003), et Newton et les origines de l'analyse : 1664-1666, A. Blanchard (2005). De larges extraits du premier sont proposés ici. Ces textes pourront utilement accompagner les séquences vidéo dans la perspective d’une utilisation dans l’enseignement.
L’enfance et l’adolescence (p. 23-25)
Les premiers cahiers : notes de lecture d’un autodidacte (p. 30 ss.)
Tangentes et aires (p. 43-44)
Vers la théorie des fluxions (p. 54-55)
Vers la théorie des fonctions (p. 71)
Rudolf Bkouche, Université des Sciences et Techniques de Lille.
Texte publié en 2006 dans: Proceedings of 4th International Colloquium on the Didactics of Mathematics, volume II, édité par M. Kourkoulos, G. Troulis, C. Tzanakis, Université de Crète".
Résumé - Lorsque nous disons que la géométrie élémentaire se situe au carrefour des sciences mathématiques et des sciences physiques, nous signifions d'une part que les objets de la géométrie ont une origine empirique, d'autre part que leur étude relève de la méthode déductive. En cela la géométrie élémentaire peut être considérée comme participant de la physique des corps solides. La géométrie élémentaire, sous la forme que lui a donnée Euclide, apparaît ainsi comme la première étude rationnelle de phénomènes naturels (les corps solides), devenant ainsi un modèle lorsque, avec la révolution scientifique du XVIIe siècle, la physique est devenue un chapitre des mathématiques, le développement de la physique s'inscrivant dans la continuité de l'œuvre euclidienne d'une part et d'autre part pouvant être considéré comme la réalisation du programme des Seconds Analytiques. Une telle conception implique que l'enseignement de la géométrie élémentaire participe à la fois de l'enseignement des sciences mathématiques et de l'enseignement des sciences physiques. On peut dire, en contrepoint, que les mathématiques sont un chapitre de la physique, point de vue exprimé par le mathématicien Vladimir Arnold (1998).
Importer l'article en version pdf
Karine Chemla, Directrice de Recherches, Equipe REHSEIS (CNRS et Université Paris 7)
Résumé - Cette interview en six séquences présente le traité mathématique le plus ancien qui nous ait été transmis par la tradition des lettrés en Chine. Karine Chemla nous parle du traité lui-même, mais aussi de ses commentaires et de leur manière singulière d'aborder des questions universelles (comment obtenir les méthodes les plus générales possibles? comment assurer la correction des algorithmes?), du long travail minutieux que représente l'édition critique d'un texte qui s'est transformé de générations en générations pendant deux mille ans. Et aussi des trésors que les enseignants de mathématiques et d'histoire peuvent découvrir dans ces textes anciens: des problèmes attrayants, dont les énoncés « composent une vision de la société en Chine il y a deux mille ans ».
Sommaire
1- Les mathématiques de Chine ancienne: des ressources pour
l’enseignement aujourd'hui.
2- La coopération franco-chinoise et le travail
d’édition critique des Neuf Chapitres.
3- La contenu et l’organisation du traité et ses
commentaires.
4- La place des Neuf Chapitres dans l’histoire des
mathématiques : comparaison avec les
Eléments
d’Euclide.
5- Les auxiliaires du texte : baguettes, figures et blocs.
6- La circulation des idées entre la Chine et
l’Inde.
Voir
les vidéos
(pour un meilleur
affichage, nous conseillons d'ouvrir cette page en passant par le
navigateur Mozilla)
Autres ressources, du même auteur
Anne Marie Décaillot, Université Paris 5, Equipe REHSEIS (Recherches Epistémologiques et Historiques sur les Sciences Exactes et les Institutions Scientifiques)
Résumé - Quelques résultats profonds de l'arithmétique supérieure ont une interprétation simple, visuelle et particulièrement élégante dans les mathématiques textiles. Ainsi en est-il d'un théorème de C. F. Gauss concernant la suite des restes (modulo p) des multiples d'un nombre a premier avec p. Ou d'un théorème énoncé par Pierre de Fermat sur les propriétés des nombres premiers de la forme 4n+1.Cet article est consacrée aux travaux originaux d'un mathématicien français du XIXe siècle en ce domaine. Il s'agit de l'arithméticien Edouard Lucas, connu par ailleurs pour les études de très grands nombres premiers qu'il effectue grâce à des tests puissants et rapides.
Utilisation en classe - Quelques uns des résultats d'Edouard Lucas présentés dans cet article pourraient donner matière à d'intéressants problèmes à proposer en terminale scientifique. On peut par exemple faire le lien avec la belle activité proposée par Jean-Pierre Kahane dans "Le nombre, cet inconnu", p. 11. Dès le collège, la disposition des points de liage sur un damier peut donner l'occasion de découvrir le calcul modulaire expérimentalement, de façon très visuelle et ludique.
Lire l'article en version html ou importer l'article en version pdf
 |
Marie-José Durand-Richard,
Université Paris 8, Equipe REHSEIS
(Recherches Epistémologiques et Historiques sur les Sciences
Exactes et
les Institutions Scientifiques). Article publié
conjointement avec le
site Les instruments du calcul savant. Résumé - Les ordinateurs sont souvent présentés comme la convergence entre des technologies et les avancées de la logique. Mais ils proviennent également des tentatives pour mécaniser la résolution approchée des équations différentielles, marquées par une hésitation sensible entre approximation par le discret et approximation par le continu. De la machine aux différences de Charles Babbage (1791-1871) au Meccano de Douglas R. Hartree (1897-1958), en passant par l'analyseur harmonique de Lord Kelvin (1824-1907), nous examinerons quelques-unes de ces tentatives et les problématiques qui leur sont attachées. |
Utilisation en classe - Le contenu de cet atelier ne fournit vraisemblablement pas un matériau directement utilisable dans la classe par les enseignants. Son intérêt réside plutôt dans la prise en compte de problématiques attachées à l'histoire des machines mathématiques, envisagées comme élément de la culture et de l'histoire sociale. Bien que cette dimension échappe traditionnellement à l'enseignement, j'en ai personnellement eu besoin pour réconcilier la représentation des mathématiques que je m'étais forgée au cours de mes études, avec celle que m'ont longtemps renvoyée les élèves lorsque j'enseignais au collège.Il me semble qu'elle peut notamment leur permettre de saisir là comment les interactions entre les mathématiques et les autres domaines de la connaissance interviennent dans la signification du calcul.
Pour aller plus loin - On trouvera cet article ainsi qu'une très riche documentation sur le site "Les instruments du calcul savant", développé par une équipe de six chercheurs, Konstantinos Chatzis, Ahmed Djebbar, Marie-José Durand-Richard, Joachim Fischer, Dominique Tournès et Galina Zverkina: "À travers l'exploration des instruments du calcul savant (calcul dépassant le niveau des opérations arithmétiques élémentaires), il s'agit de mettre en lumière des savoirs et des pratiques mathématiques négligés par l'historiographie traditionnelle, ainsi que des interactions jusqu'ici peu étudiées entre diverses communautés professionnelles (mathématiciens, ingénieurs, fabricants d'instruments...)."
Importer l'article de Marie-José Durand-Richard en version pdf
Denis Lanier (Lycée Malherbe de Caen) et Didier Trotoux (IUT de Caen), IREM de Basse-Normandie
Précédente édition: 1996, dans "Contribution à une approche historique de l'enseignement des mathématiques", Actes de la 6° université d'été interdisciplinaire sur l'histoire des mathématiques, Presses Universitaires de Franche-Comté, collection "Les publications de l'IREM de Besançon", p. 259-294.
Résumé - Le couple fréquence-probabilité, ainsi que la théorie instituant ce rapport qu'on peut appeler schématiquement "loi des grands nombres", est un leitmotiv de la période classique de l'histoire du calcul des probabilités. Il est au coeur du développement de la théorie et des préoccupations des probabilistes, comme de ses utilisateurs. Les programmes des lycées imposent de prendre une approche fréquentiste pour définir une probabilité. Cela pose le problème du statut de ces énoncés que l'on rassemble sous le nom de "loi des grands nombres". Peu de propositions mathématiques portent ce titre de "loi". Est-ce un théorème, comme il est utilisé habituellement pour le "théorème de De Moivre-Laplace ? Est-ce un énoncé extra-mathématique, admis comme prémisse à toute théorie scientifique ?
D'une certaine manière, pour pouvoir faire des probabilités (et en particulier les appliquer), tout se passe comme si on devait admettre que la nature suit (au moins localement) des lois, qui permettent l'élaboration d'une théorie, à l'intérieur de laquelle on démontre ensuite cette loi. Le rapprochement avec la situation du physicien, pour embarrassante qu'elle soit pour certains mathématiciens, est flagrante.
Il nous semble, d'un point de vue historique et aussi d'un point de vue pédagogique, qu'il est un peu vain de s'en tenir aux différentes définitions du concept de probabilité, en recherchant la meilleure. En revanche l'étude historique de sa mise en oeuvre et de ses problématiques nous paraît riche d'enseignements. En ce qui concerne la "loi des grands nombres", depuis son énoncé initial par Jacques Bernoulli jusqu'à la résolution du problème limite classique par Kolmogorov, le travail des probabilistes consiste à chercher à comprendre l'énoncé, à le préciser, à en évaluer la portée, à tenter de simplifier la démonstration. Du point de vue de l'histoire interne des mathématiques, il y a là, pendant deux siècles, un travail sur le texte lui-même qui est tout à fait fascinant. On verra dans la suite que ces questions ne se posaient que si l'on voulait appliquer les probabilités à d'autres domaines que les jeux de hasard. On verra aussi qu'elles recoupaient initialement des préoccupations métaphysiques - si la nature suit la loi des grands nombres, c'est qu'il y a quelqu'un qui a fabriqué le dé, d'où l'existence de Dieu - qu'on se garde bien d'aborder maintenant dans nos classes.
L'histoire de la loi des grands nombres est jalonnée par quelques grands textes sans oublier que l'histoire ne s'arrête pas là. Les trois premiers pas sont marqués par Jacques Bernoulli et l'Ars Conjectandi (1713), Abraham De Moivre et la Doctrine of Chances (1756), Pierre-Simon de Laplace et la Théorie Analytique des Probabilités (1812). Nous avons choisi de centrer le travail de l'atelier sur le texte, moins connu, de De Moivre et sa reprise par Laplace. On trouvera en annexe des extraits des ouvrages de De Moivre et Laplace.
Importer l'article en version pdf
Denis Lanier (Lycée Malherbe de Caen) et Didier Trotoux (IUT de Caen), IREM de Basse-Normandie
Précédente édition: 1998, dans "Analyse et démarche analytique", IREM de Reims, p. 231-286.
Introduction - La formule dite de Stirling, qui donne une évaluation de n! pour les grandes valeurs de n, est au centre des travaux menés au début du XVIIIe siècle sur les problèmes probabilistes de passage à la limite et d'approximations. Cet article peut se présenter comme un complément au texte sur le théorème de de Moivre-Laplace. La découverte des évaluations de n! par de Moivre et Stirling a donné lieu à des travaux concomitants de ces deux mathématiciens avec des échanges de correspondance, des corrections mutuelles d'erreurs. Ces travaux se situent à un moment que l'on peut qualifier de paradoxal dans l'histoire des mathématiques. En effet les méthodes infinitésimales se développent alors de plus en plus ; elles permettent d'aborder et de résoudre des questions nouvelles. Mais la véracité des résultats obtenus ne peut plus être légitimée par une synthèse démonstrative à la grecque. Il faut donc innover, expérimenter, confronter les résultats obtenus par différentes méthodes ou différents auteurs, avant de pouvoir être sûr de la scientificité d'un énoncé. Nous savons de plus aujourd'hui que certains outils étaient employés sans la rigueur (au sens moderne du terme) nécessaire. Ce sont donc les tours et détours des démarches analytiques du début du XVIIIe siècle que nous voudrions montrer dans ce texte.
Autres ressources sur les probabilités, sites externes
|
Utilisation en classe - On peut utiliser la documentation de cet article à tous les niveaux de l'enseignement, depuis la fabrication de tables de multiplication au collège jusqu'à la présentation des propriétés arithmétiques de la numération sexagésimale et du calcul en virgule flottante au lycée. A partir des exercices de calcul mésopotamiens, une réflexion plus large peut être engagée dans le cadre de la formation des enseignants, par exemple sur le concept de nombre, le principe de position, les liens entre l'apprentissage de l'écriture et du calcul.
|
Lire l'article ou importer en version pdf. |
André Warusfel
Résumé: A l’origine du calcul littéral figure notamment la résolution des équations algébriques, de Babylone à Galois. Le problème de la résolution des équations P(x)=0 où P est un polynôme donné possède plusieurs types de réponses, selon ce que l’on en attend : par exemple, développements décimaux d’ordre donné des solutions (heureusement en nombre fini), construction géométrique de segments ayant pour longueurs les valeurs des racines positives de l’équation, algorithmes basés sur des extractions de racines ou emploi de fonctions spéciales (elliptiques par exemple). Leur étude a été un facteur très important de la naissance et du développement des techniques de calcul (littéral ou géométrique). Leur histoire est jalonnée par une liste impressionnante de créateurs : les babyloniens, Euclide, Diophante, Al Khwarizmi, Cardan, Viète, Descartes, Newton, Lagrange, Abel et Galois pour ne citer que ceux-là. Enfin l’informatique est venue modifier, parfois de manière importante, les points de vue que nous avions il y a cinquante ans sur ce thème. Le but de l’intervention est de préciser, à chaque fois de manière simple et assez succincte, que fut l’apport de chacun d’entre eux.
Utilisation en classe - Les enseignants de tous les niveaux trouveront des idées intéressantes à faire découvrir à leurs élèves. Par exemple, on peut dès le collège résoudre des équations du second degrè grâce à la méthode de complétion du carré, ou démontrer géométriquement les identités remarquables. Mais ce sont surtout les enseignants de première qui trouveront dans cet article une excellente introduction au cours sur les équations du second degré.
Importer l'article en version pdf
Ressources externes