La divination sikidy à Madagascar

La version proposée par CultureMATH est  différente de celle de Pour la Science: l'iconographie a été augmentée, la mise en page est plus sobre, mais le texte est  sur certains points, plus complet. Des compléments mathématiques sont donnés par Marc Chemillier dans deux encarts. Enfin, 5 séquences vidéos illustrent le propos des l'auteurs.

Article déposé le 18 janvier 2010. Toute reproduction pour publication ou à des fins commerciales, de la totalité ou d'une partie de l'article, est interdite. Toute reproduction à des fins strictement pédagogiques dans le cadre limité d'une formation, de la totalité ou d'une partie de l'article, est autorisée sous réserve d'un accord préalable de l'éditeur (ENS Ulm) et de la mention explicite des références éditoriales de l'article.

  La divination malgache, appelée sikidy, est une pratique en usage sur tout le territoire de Madagascar, dont les principes sont directement empruntés à la géomancie arabe, qui s'est diffusée en Afrique dans le sillage de l'Islam. Au Moyen-Âge, la géomancie est décrite en occident à partir du XIIe siècle dans des textes latins comme le traité Ars geomancie de Hugues de Santalla (voir Figure 1). Les Malgaches semblent s'être fait une spécialité de ce mode de divination, et la plupart des populations de l'île pratiquent les mêmes règles de construction formelle d'origine arabe. Les variantes d'une population à l'autre ne concernent que des aspects particuliers (à l'exception toutefois d'un système simplifié de divination utilisé par certaines populations). Les Malgaches ont un besoin essentiel de devins traditionnels pour tous les aspects de leur vie quotidienne, et pour cette raison, on en trouve dans chaque village ou quartier de grande ville.

    La divination sikidy consiste à disposer sur le sol des graines de fano (une sorte d'acacia), sous la forme d'un tableau, dans le but de lire la destinée à travers certaines configurations de graines qui apparaissent dans ce tableau. La procédure de placement des graines comporte une partie produite au hasard (où se manifeste la destinée), et une partie construite à partir de la précédente selon des règles précises. Cette partie calculée du sikidy met en œuvre, comme on va le voir, des propriétés formelles élaborées qui sont celles d'une véritable structure algébrique.

    Il existe plusieurs études sur les propriétés algébriques de la divination sikidy, en particulier celle de Marcia Ascher (ainsi qu'une autre non publiée d'un  mathématicien de l'université de Tananarive, Manelo Anona). Leur source éthnographique commune est le travail d'un ancien administrateur colonial et grand connaisseur des traditions malgaches, Raymond Decary, qui a photographié des devins dès le début du XXe siècle (voir Figure 2). Un autre travail réalisé plus récemment par un anthropologue de  l'université de Tuléar, Jean-François Rabedimy, fournit également de nombreuses observations sur le sikidy. Les études d'ethnomathématique consacrées à ce sujet abordent les propriétés formelles du système in abstracto, indépendemment des processus mentaux effectivement mis en œuvre par les devins. Nous avons mené entre 2000 et 2007 une recherche sur les aspects algébriques de la divination à Madagascar, dont la particularité est précisément d'associer, de façon étroite, l'analyse mathématique et l'enquête de terrain. Les méthodes employées sur le terrain pour accéder aux mécanismes mentaux qui « incarnent » les différentes propriétés étudiées sont principalement, outre les techniques habituelles de l'enquête ethnographique, l'utilisation de la vidéo pour capter certains gestes explicatifs ou certaines étapes de construction, ainsi que des tests chronométriques dont le but est d'expliciter certaines opérations mentales particulières.[1]

Figure 2                                                                                                                   Devins Antandroy (sud de Madagascar) photographiés par Raymond Decary en 1924. Curieusement, le tableau de graines ne respecte pas la construction usuelle (en particulier, il n'a que sept colonnes inférieures au lieu de huit).

    La divination commence par le brassage des graines répandues sur le sol, en récitant diverses incantations. Puis le devin prend une poignée de graines au hasard qu'il pose en tas devant lui, et retire les graines deux par deux en les faisant glisser avec l'index et le majeur. L'élimination par paires revient à faire une division euclidienne du nombre initial par deux. En conséquence, le reste ne peut prendre que deux valeurs, 1 ou 2. On voit que ce reste déterminé par le nombre de graines contenues initialement dans la poignée, est le résultat d'un tirage aléatoire qui manifeste la destinée du consultant (voir Vidéo 1). L'opération de tirage est réitérée seize fois, et les seize valeurs sont placées dans un tableau carré de dimensions quatre par quatre appelé renin-tsikidy (matrice mère). Ce tableau définit huit figures initiales, qui sont ses quatre lignes et ses quatre colonnes.


    En dessous de la matrice mère, on construit huit nouvelles colonnes de quatre éléments chacune, appelées les filles, déduites des figures initiales en appliquant la règle de calcul suivante :

- une graine et une graine donnent deux graines,
- deux graines et une graine donnent une graine,
- deux graines et deux graines donnent deux graines.

On reconnaît la loi de composition interne du groupe à deux éléments noté traditionnellement ℤ/2ℤ. On note 0 et 1 les deux éléments de ce groupe. La paire de graines correspond à l'élément neutre 0, et la graine isolée correspond à 1. Les figures du sikidy sont des quadruplets d'éléments de ce type, et l'addition de deux figures consiste à appliquer la règle ci-dessus à chacune des quatre composantes. Ainsi, l'ensemble des figures se trouve muni d'une structure algébrique de groupe commutatif, qui est celle du groupe produit (ℤ/2ℤ)⁴ des quadruplets de ℤ/2ℤ. Plus précisément, l'addition de deux figures est une opération commutative, et associative. Enfin, l'opération possède un élément neutre qui est le quadruplet (2, 2, 2, 2), et chaque figure est son propre inverse, car on vérifie aisément qu'en additionnant une figure avec elle-même, on obtient toujours l'élément neutre (2, 2, 2, 2).

    Les filles sont définies en plusieurs générations. Les filles directes dépendent des lignes et colonnes de la matrice mère, puis de nouvelles filles sont construites à partir des précédentes.  Le tableau 1 montre un exemple de configuration de sikidy, en indiquant les numéros des figures (1 à 4 pour les colonnes mères comptées à partir de la droite, 5 à 8 pour les lignes mères lues de droite à gauche, puis 9 à 16 pour les filles).

Les noms vernaculaires de ces seize positions, et le principe de calcul des filles, sont les suivants :

- colonne mère : 1 = tale,
- colonne mère : 2 = maly,
- colonne mère : 3 = fahatelo,
- colonne mère : 4 = bilady,
- ligne mère : 5 = fianahana,
- ligne mère : 6 = abily,
- ligne mère : 7 = alisay,
- ligne mère : 8 = fahavalo,

- fille de première génération : 15 = safary = 1 + 2,
- fille de première génération : 13 = asorita = 3 + 4,
- fille de deuxième génération : 14 = saily = 13 + 15,

- fille de première génération : 11 = haja = 5 + 6,
- fille de première génération : 9 = fahasivy = 7 + 8,
- fille de deuxième génération : 10 = ombiasy = 9 + 11,

- fille de troisième génération : 12 = haky = 10 + 14,
- fille de quatrième génération : 16 = kiba = 12 + 1.

    Les seize positions ainsi définies peuvent être vues comme des applications P_i ,  i = 1, ..., 16, associant à chaque matrice mère M une certaine figure P_i(M). Or l'ensemble des matrices mères (ℤ/2ℤ)¹⁶ peut être muni de la même structure algébrique de groupe commutatif que l'ensemble des figures (ℤ/2ℤ)⁴. L'addition de deux matrices consiste alors à additionner les coefficients en même position. Il est facile de voir que, quelle que soit l'application P considérée parmi celles définies ci-dessus, si M et N sont deux matrices mères, la figure apparaissant en P_i(M + N) n'est autre que l'addition des deux figures P_i(M) + P_i(N). Mathématiquement, on dira que P_i est un morphisme de groupe. Cette remarque a des conséquences intéressantes sur le plan formel. En particulier, l'ensemble des figures pouvant apparaître dans une position donnée du tableau (parmi les seize positions) est nécessairement un sous-groupe du groupe des figures, c'est-à-dire un sous-ensemble de figures qui est stable pour l'addition (Cf. Encart1).

Les figures paires et impaires

Les figures de sikidy sont au nombre de seize, et portent des noms vernaculaires. Nous utilisons la terminologie de la population Antandroy (une ethnie du sud de Madagascar), car les termes varient légèrement d'une ethnie à l'autre. De plus, les devins distinguent deux classes importantes de figures, celles dont le nombre total de graines est pair, appelées mpanjaka (princes), et celles dont le nombre total de graines est impair, appelées andevo (esclaves) :

1) princes :

tareky = (1, 1, 1, 1),
alasady = (1, 1, 2, 2),
adalo = (1, 2, 1, 2),
alokola = (1, 2, 2, 1),
alotsimay = (2, 1, 1, 2),
alohotsy = (2, 1, 2, 1),
adabara = (2, 2, 1, 1),
asombola = (2, 2, 2, 2).

2) esclaves :

karija = (1, 1, 1, 2),
alimizanda = (1, 1, 2, 1),
alakarabo = (1, 2, 1, 1),
renilaza = (1, 2, 2, 2),
alakaosy = (2, 1, 1, 1),
alaimora = (2, 1, 2, 2),
alibiavo = (2, 2, 1, 2),
alikisy = (2, 2, 2, 1).

    Cette distinction prince/esclave joue un grand rôle dans la technique de divination. Elle intervient d'abord dans une propriété formelle du système de construction des tableaux, qui veut que la figure apparaissant en colonne 12 (haky) est nécessairement un prince. On peut le vérifier dans le tableau 1  (ci-dessus), où la figure en position 12 est alasady (1, 1, 2, 2), qui est bien un prince. Il est possible de justifier cette propriété par une démonstration mathématique, dont l'idée intuitive est que la somme des graines en colonne 12 est égal, modulo 2, au double de la somme de tous les éléments de la matrice mère, une fois dans l'ordre des lignes, et une fois dans l'ordre des colonnes, ce qui implique que le nombre obtenu est nécessairement pair. On peut même aller plus loin, et montrer que toute figure paire peut apparaître dans cette position à l'intérieur d'un tableau. Il suffit pour cela de construire une matrice mère dont les éléments sont égaux à 2, sauf quelques 1 placés de façon ad hoc pour obtenir la figure voulue. L'ensemble des figures pouvant apparaître en position 12 est donc égal à l'ensemble de toutes les figures paires, qui est donc un sous-groupe du groupe des figures. Par un raisonnement analogue, on montre qu'une figure quelconque peut apparaître dans toute position secondaire exceptée la colonne 12. Ainsi, pour toute position secondaire P considérée comme un morphisme, comme on l'a vu plus haut, l'image Im(P) est soit le groupe des seize figures lui-même, soit dans le cas de la colonne 12 le sous-groupe des huit figures paires.

    Tous les devins connaissent cette propriété de la colonne 12 et elle est utilisée comme un moyen de vérifier qu'il n'y a pas eu d'erreur dans la construction du tableau. La présence d'un prince dans cette position est une condition sina qua none pour qu'un tableau puisse être interprété. Mais ceci ne dit rien sur la manière dont les devins conceptualisent la notion de « parité » elle-même. Sont-ils conscients que la distinction princes/esclaves repose sur un critère arithmétique, et si oui, comment l'expriment-ils ? La réponse nous a été donnée de façon inattendue par Raymond, un devin de l'ethnie Mahafaly habitant Tuléar, au sud-ouest de Madagascar. Il a placé les huit figures paires les unes à côté des autres (voir Figure 3, en haut à gauche). Puis dans chaque figure, il a fait glisser toutes les graines isolées de manière à les apparier avec une autre graine de la même figure. Le résultat est une succession de configurations dans lesquelles les graines sont groupées par deux, comme on le voit sur la photo en haut à droite. Il a commenté cette procédure en disant que les princes sont tsy ota. Ce terme, qui signifie littéralement « sans péché », est une manière d'exprimer le concept de nombre pair, car cela revient à dire qu'en procédant à l'appariement des graines, on ne laisse aucune graine isolée. Pour les huit figures impaires, la procédure est la même, mais Raymond a fait observer qu'après appariement, il reste toujours une graine isolée dans chaque figure, qu'il a fait glisser vers le bas, comme on le voit sur la photo de droite ci-dessous. Il a qualifié le résultat de ota, ce qui traduit le concept de nombre impair.

Figure 3 - Concept de parité Photos : Annick Armani 2001 En haut, les 8 figures paires (à gauche), dont les graines sont groupées par couples (à droite)- Vidéo 2 En bas, les 8 figures impaires (à gauche), avec leur reste (à droite) - Vidéo 3

   
    Nous avons effectué des tests chronométriques pour étudier l'opération mentale réellement mise en œuvre par les devins dans la distinction des figures paires et impaires, et pour la comparer à celle de sujets non devins. Sur l'écran d'un ordinateur portable, 48 figures de sikidy sont proposées successivement.  Le sujet doit reconnaître celles qui sont des princes et celles qui sont des esclaves en appuyant sur une touche à gauche ou à droite du clavier. Le point remarquable qui est révélé par ces tests est que pour des sujets non devins, la figure asombola (2, 2, 2, 2), qui a huit graines et dans laquelles toutes les graines sont groupées par couples, permet une détection beaucoup plus rapide de la parité du nombre de graines. On observe en effet que la courbe présente systématiquement un pic inférieur dans le temps de réaction lorsque cette figure apparaît. D'une manière similaire, la figure tareky (1, 1, 1, 1), qui a quatre graines, correspond aussi à un minimum de la courbe. Dans le cas des sujets devins, en revanche, aucune propriété de ce type n'apparaît. Il est vraisemblable que pour eux, la reconnaissance prince/esclave est un mécanisme mental tellement intégré que le comptage des graines dans les figures est inutile. Ces tests montrent également que la prodécure de regroupement des graines décrite ci-dessus par Raymond, pour classer les figures en ota et tsy ota, est un moyen théorique d'expliquer la distinction prince/esclave, mais ne correspond pas à une procédure effective utilisée dans la pratique.

Figure 4 - Expérimentation en psychologie cognitive   Tests de reconnaissance de la parité à l'aide de SuperLab est un logiciel d'expérimentation en psychologie cognitive (sujet non devin en haut, sujet devin en bas). La courbe donne les temps de réponse en millisecondes pour une série de 48 figures. Une deuxième courbe, dans le rectangle inférieur, indique les nombres de graines des figures (valant de 4 à 8). On voit nettement, dans le cas du sujet non devin, un pic inférieur marqué pour les valeurs extrêmes des nombres de graines 4 et 8.

    <sup>Les figures paires et impaires se combinent en respectant une règle précise, qui résulte de la structure mathématique sous-jacente au sikidy  :


En effet, l'ensemble des figures paires est, comme on l'a vu plus haut, un sous-groupe du groupe des figures. Dans ce cas, on peut former le quotient du groupe par ce sous-groupe, et l'opération d'addition induit dans le groupe quotient une opération de combinaison des classes mpanjaka et andevo qui est exactement celle définie par la règle ci-dessus. Les devins ne semblent pas avoir de difficulté à manipuler les combinaisons de classes. Nous ne savons pas si cette règle de combinaison joue ou non un rôle effectif dans la pratique de la divination, mais elle pourrait en jouer un dans une méthode de calcul des filles décrite dans la section suivante.</sup>

Calcul mental des figures secondaires

    Les positions de gauche à droite des filles dans la partie inférieure du tableau ne correspondent pas, comme on l'a vu, à l'ordre dans lequel elles sont construites. Mais il arrive parfois que l'ordre de construction soit modifié pour se rapprocher d'un ordre gauche-droite ou droite-gauche. Nous avons noté plusieurs cas de ce type, dont certains nous ont été révélés a posteriori par l'enregistrement vidéo que nous avons fait des séances de travail.
   
    Dans un cas d'inversion (voir Figure 5), Njarike, devin Antandroy de Tuléar, a construit la colonne 10 avant 9, alors que 10 résulte de 9 + 11. Le tableau complet correspondant est le tableau 1 ci-dessus. Mais dans cette situation concrète, l'inversion pourrait s'expliquer par des circonstances particulières. L'élément apparu précédemment en 11 est la figure asombola (2, 2, 2, 2), qui est l'élément neutre du groupe. Pour cette raison, Njarike peut prévoir que 9 et 10 = 9 + 11 contiennent nécessairement la même figure, et sont donc interchangeables. Il lui est alors possible, dans ces conditions, de placer cette figure en 10 avant de la recopier en 9. Il se trouve que dans tous les cas que nous avons enregistrés où une inversion se produit, elle concerne l'apparition de l'élément neutre (2, 2, 2, 2). D'une certaine manière, on peut dire que l'inversion par rapport à l'ordre de construction normal traduit la conscience qu'ont les devins du rôle d'élément neutre joué par la figure asombola (2, 2, 2, 2).

Figure 5 - Inversion dans l'ordre de construction Photo :  Victor Randrianary 2003 L'ordre "officiel" est le suivant: la première fille construite est la 15, puis 13, et 14, puis 11. En principe viennent ensuite  9 et 10. Et enfin 12 et 16. On voit sur cette image que le devin a placé 15-13-14-11 et 10. Il  construit donc  9 après 10 - Vidéo 4

    Pourtant, il est possible que les devins aient utilisé un ordre de construction gauche-droite des figures secondaires de manière plus systématique. C'est ce qu'affirme Jean-François Rabedimy dans son ouvrage sur le sikidy. La méthode qu'il décrit revient à utiliser, sur le plan mathématique, l'associativité de l'opération de groupe pour calculer les figures secondaires de seconde et troisième générations 10, 14 et 12 non plus à partir de celles de première génération 9, 11, 13, 15, mais en se référant directement à la matrice mère.

    Pour la colonne 14 de seconde génération, on a en effet, par associativité de l'opération de groupe :

14 = 13 + 15 = 1 + 2 + 3 + 4,

c'est-à-dire que 14 est la combinaison des quatre colonnes de la matrice mère. Donc les quatre composantes de cette figure sont données par les sommes des graines dans les quatre lignes, c'est-à-dire par les classes des figures correspondantes (prince ou esclave). Or on a vu que les devins sont habitués à déterminer la classe d'une figure. En attribuant à cette classe les valeurs 1 (esclave) ou 2 (prince), ils peuvent obtenir les quatre éléments de la colonne 14 en déterminant classe(5), classe(6), classe(7), classe(8), ce qui peut être fait d'un seul coup d'œil à partir des lignes 5, 6, 7, 8 de la matrice mère. De la même manière, pour la colonne 10, on a :

10 = 9 + 11 = 5 + 6 + 7 + 8,

donc les quatre éléments de la colonne 10 s'écrivent classe(1), classe(2), classe(3), classe(4), et peuvent être déterminés par un simple coup d'œil sur les colonnes 1, 2, 3, 4 de la matrice mère.

    Pour la colonne de troisième génération 12 = 10 + 14, on a vu dans la section précédente que les devins n'ont aucune difficulté pour manipuler les combinaisons de classes (prince + prince, prince + esclave, esclave + esclave). Il ne leur est donc pas impossible, en regardant la matrice mère, d'effectuer les combinaisons


qui donnent précisément les quatre éléments de la colonne 12. Ainsi, toutes les filles jusqu'à la colonne 15 peuvent être calculées par un simple regard sur la matrice mère. En calculant ainsi les filles de gauche à droite, la dernière 16 = 1 + 12 peut alors être obtenue à partir de 1 et 12 qui ont déjà été calculées.

    Nous avons fait des expériences de calcul mental des filles d'un tableau, dans l'ordre normal de construction d'une part, et dans l'ordre gauche-droite d'autre part. On construit une matrice mère au hasard, et le devin doit dire les noms des figures apparaissant dans les positions secondaires, sans les réaliser avec les graines. Il s'avère qu'ils sont capable d'effectuer ce type de calcul de tête, et quel que soit l'ordre demandé. Njarike, ou Falesoa, un jeune et brillant devin Antandroy de Tuléar, n'ont eu aucune difficulté à réaliser le calcul dans les deux sens, normal et gauche-droite.
 

Tableaux remarquables toka et fohatse

    Les devins étudient certains tableaux particuliers de sikidy, dont l'apparition dans une séance de divination est un événement qui nécessite une attention spéciale. Une première catégorie de tableaux, appelés toka (ou into), fait intervenir une répartition des seize figures selon les points cardinaux. Nous indiquons ici la répartition Antandroy (car l'orientation des figures varie d'une ethnie à l'autre, et il en résulte que les ethnies n'ont pas les mêmes toka) :

- figures du nord : renilaza, alibiavo, karija, adalo
- figures du sud : alimizanda, alasady, tareky, asombola
- figures de l'est : alaimora, adabara, alotsimay
- figures de l'ouest : alikisy, alakarabo, alokola, alohotsy, alakaosy

    Par définition, les tokan-tsikidy sont les tableaux dans lesquels l'un des points cardinaux n'apparaît qu'une seule fois parmi les seize positions. Comme on le voit, cette définition se situe sur un plan purement logique, en mettant en exergue une propriété d'unicité. Les devins jettent parfois une poudre sur certaines figures d'un tableau remarquable, pour fabriquer des talismans considérés comme dangereux. La photo ci-dessous, prise chez Boribory, un devin très consulté à Tuléar, montre un toka pour la figure asombola (2, 2, 2, 2) en colonne 2, qui est la seule du tableau orientée au sud, ce qui lui confère un pouvoir particulier. Une poudre a été versée sur les graines de cette colonne, ainsi que sur celles des figures du tableau orientées à l'est (colonne 1, ligne 5, filles 9, 14, 15, 16).

Figure 6 Photo : Annick Armani 2001 Un toka dont certaines colonnes sont recouvertes de poudre.

  
    Le prestige des devins repose en partie sur la quantité de tokan-tsikidy qu'il connaît. C'est pourquoi ils recherchent activement ces tableaux particuliers. L'un des résultats majeurs obtenus au cours des missions de terrain réalisées dans le cadre de ce programme a été la découverte de l'existence de carnets, dans lesquels ils notent ces configurations remarquables. Nous avons eu la chance exceptionnelle de pouvoir en photographier et même photocopier certaines pages. L'un d'eux, appartenant à Jean-Bosco Randriampaniry, devin Antaimorona du quartier Anosipatrana à Tananarive, a révélé que les devins ont recours à des méthodes de classification systématiques de ces tableaux, comme en atteste la photo ci-après (voir Figure 7). La page est divisée en cases, dans lesquelles sont rangées des configurations de graines (seules les matrices mère sont notées). Mais l'une des cases est vide, ce qui prouve que le devin anticipait l'existence de ce type de configuration, alors même qu'il n'en avait jamais rencontré effectivement.

Figure 7 - Classement systématique de toka   Photo : Marc Chemillier 2001

    Nous avons développé un programme informatique qui permet de calculer tous les tokan-tsikidy. Par construction, un tableau est entièrement déterminé par les seize coefficients de sa matrice mère. Il y a donc exactement 2¹⁶ = 65.536 tableaux possibles, et il suffit de quelques secondes à un ordinateur portable pour effectuer un parcours exhaustif de ces tableaux. De cette manière, on peut montrer qu'il existe 15.751 tokan-tsikidy (dans le système de points cardinaux Antandroy). Ce calcul montre également l'existence de certaines impossibilités :

- trois figures du sud (tareky, asombola, alasady) ne peuvent être toka ni en 11, ni en 15,
- quatre figures de l'ouest (alakarabo, alokola, alohotsy, alakaosy) ne peuvent être toka ni en 9, ni en 13,
- de plus, alohotsy ne peut être toka en 10.

La plupart des devins connaissent ces impossibilités, quoique cette connaissance, telle que nous avons pu l'observée, ne procède pas d'un argument logique, mais seulement d'un constat hérité de la tradition. Celle-ci n'a jamais rapporté de cas où les impossibilités seraient mises en défaut.

    L'autre catégorie de tableaux particuliers qui intéresse les devins concerne ceux, appelés sikidy fohatse, qui sont définis par le fait qu'une même figure est répétée plus de huit fois à l'intérieur du tableau. Des tableaux avec sept répétitions ou moins peuvent aussi être considérés comme fohatse, mais le chiffre huit est un seuil sur le plan logique. En effet, à partir de huit répétitions ou plus, certaines impossibilités apparaissent. Notre programme informatique montre qu'il est toujours possible de construire un tableau en répétant exactement sept fois une figure donnée, quelle que soit cette figure, mais qu'il est impossible d'obtenir exactement huit répétitions des figures suivantes : alokola, alikisy, alaimora, renilaza, alibiavo, adalo, tareky. Pour certaines figures, on peut construire un tableau avec plus de huit répétitions, et dans certains cas indiqués ci-après, la solution est de plus unique :

        16 asombola,
        11 karija, 11 alimizanda, 11 alakarabo,
        10 alakaosy,
        9 tareky, 9 alimizanda, 9 adalo, 9 karija, 9 alokola,
        8 alotsimay, 8 alohotsy, 8 alakaosy.

Les devins connaissent la plupart de ces configurations remarquables. La catégorie des sikidy fohatse, qui semble très utilisée par eux, est passé relativement inaperçue dans les études sur le sikidy. 

Transposition de la matrice mère

    Dans leur recherche de tokan-tsikidy, les devins utilisent une opération bien connue en mathématiques, appelée transposition de matrice, qui consiste à échanger les lignes et les colonnes d'une matrice, à ceci près que l'opération d'algèbre linéaire consiste à faire l'inversion par rapport à la première diagonale, alors que les devins malgaches la font par rapport à la deuxième (la ligne du haut devient la colonne de droite, et non de gauche - Voir  Vidéo 5). Comme le système du sikidy fait jouer des rôles quasi-symétriques aux lignes et aux colonnes de la matrice mère, cette transformation a la propriété de laisser globalement presque invariant l'ensemble des figures apparaissant dans un tableau. Plus précisément, si l'on échange les lignes et les colonnes, on constate que les filles 9, 10, 11 sont échangées avec les filles 13, 14, 15, et que la colonne 12 est inchangée. Seule la colonne 16 est susceptible de faire apparaître une nouvelle figure, non présente dans le tableau initial. Ainsi, la transposition de la matrice mère modifie au plus une figure dans un tableau de sikidy, de telle sorte que si celui-ci était toka au départ, il y a de fortes chances pour qu'il le reste après transposition (Cf. Encart 2). Cette opération apparaît donc comme un moyen d'obtenir, dans de nombreux cas, un nouveau toka à partir d'un toka donné. Le terme Antandroy qui sert à la désigner est avaliky, qui veut dire « inverser » dans le dialecte du sud.


    L'opération de transposition apparaît d'elle-même quand on s'intéresse aux tableaux toka. Dans la section précédente, on a énuméré des impossibilités, pour certaines figures, d'être toka dans certaines positions. Si l'on regarde les positions obtenues, on constate qu'elles sont liées entre elles par l'opération de transposition. On a vu en effet que trois figures du sud ne peuvent être toka ni en 11, ni en 15. Or la transposition de la matrice mère a justement pour effet d'échanger 11 et 15. De même, quatre figures de l'ouest ne peuvent être toka ni en 9, ni en 13, et de la même manière, la transposition échange 9 et 13. Les devins, qui connaissent ces impossibilités, n'ont pas manqué de remarquer qu'elles se groupent par couples de colonnes échangeables sous l'effet d'une transposition. En revanche, la dernière impossibilité (alohotsy toka en 10) est isolée, car la colonne 14 associée par transposition permet d'obtenir des toka avec la figure alohotsy. Ici, la dernière colonne 16 est modifiée par l'opération de transposition.

    Un autre cas intéressant faisant intervenir l'opération de transposition est celui du triple toka. Lors d'une séance de travail à Majunga avec Jean-François Rabedimy, celui-ci nous a montré un exemple de tableau trois fois toka, en conjecturant qu'il n'en existe qu'un seul de ce type (voir tableau 2). Ce tableau est connu des devins, par exemple de Namdro, devin Antandroy habitant Majunga.


 
 

Tableau 2 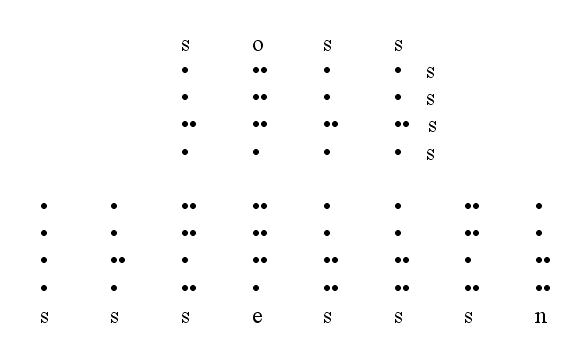Tableau triple toka de Jean-François Rabedimy

   Le calcul par ordinateur a confirmé l'intuition de Jean-François Rabedimy. En effet, la solution est bien unique, mais cela n'est vrai qu'à une transposition près, c'est-à-dire qu'il existe exactement deux matrices mère donnant un tableau trois fois tokan, et ces deux matrices sont transposées l'une de l'autre. On notera d'ailleurs que la première ligne est égale à la colonne de droite, et ceci est une condition suffisante pour qu'un tableau reste toka après transposition.

Bibliographie

Ascher M., « Malagasy Sikidy: A Case in Ethnomathematics », Historia Mathematica, 24, 1997, p. 376-395.

Chemillier M., Jacquet D., Randrianary V., Zabalia M., « L'art des devins à Madagascar », Pour la science, dossier n° 47 « Mathématiques exotiques », 2005, p. 90-95.

Chemillier M., Jacquet D., Randrianary V., Zabalia M., « Aspects mathématiques et cognitifs de la divination sikidy à Madagascar », L'Homme, 182, 2007, p. 7-40.

Chemillier M., « Mathématiques de tradition orale », Mathématiques et sciences humaines, 178, 2007 (2), p. 11-40 (Texte au format pdf ici).

Chemillier M., « Divination et rationalité à Madagascar », K. Chemla (éd.), Actes du colloque de synthèse Histoire des savoirs, décembre 2007, p. 241-258 (Texte au format pdf ici).

Chemillier M., Les Mathématiques naturelles, Paris, Odile Jacob, 2007.

 Chemillier M., « Les mathématiques dans les sociétés sans écriture », Tangente, l'aventure mathématique, hors-série n° 33 « Nombres, les nouveaux secrets », mai 2008, p. 6-9.

Chemillier M., « The development of mathematical knowledge in traditional societies. A study of Malagasy divination », Paul Dixon (ed.), special issue of Human Evolution, vol. 24(4), 2009, p. 287-299.

Chemillier M., « Ethnomathematics », Nick Thieberger (ed.), The [Oxford] Handbook of Linguistic Fieldwork, chapter 12, Oxford University Press [to appear, 2010].

Decary R., La divination malgache par le sikidy, Librairie orientaliste Paul Geuthner, 1970.

Rabedimy J.-F., Pratiques de divination à Madagascar. Technique du Sikidy en pays sakalava-menabe, ORSTOM, n°51, 1976.

Sadi R., « Configurations et probabilités d'occurrence de la figure unité en P15 en géomancie additive et en géomancie multiplicative », R. Jaulin, Géomancie et Islam, Paris, Christian Bourgois, 1989, p. 37-46.

Liens

SIKIDI : Divination à Madagascar

^{Page web de Marc Chemillier}

Site geomance

^{Haut de page}

^{[1] Programme  financé par l'action concertée incitative « Cognitique » pour la période 2001-2004, cette recherche associe l'équipe d'intelligence artificielle du GREYC à Caen (CNRS UMR 6072), le laboratoire de psychologie cognitive de Caen (EA 1774) et le laboratoire CNRS UMR 8574 du Musée de l'Homme. Elle a été poursuivie en 2004-2007 dans le cadre de l'action concertée incitative « Histoire des savoirs ».}