[8] en bibliographie
Version [pdf ] (17 p., 1.2 Mo).
|
SOMMAIRE 1 . La question de la quadrature du cercle 2. Ad Quadrandrum Circulum 2.1 Discussion du fragment cartésien 2.2 Le commentaire d'Euler 3. Le problème de l'exactitude 3.1 Exactitude et recevabilité 3.2 Constructions point par point 3.3 Constructions génériques et spécifiques 3.4 Clavius 4. Non recevabilité de la quadrature du cercle 5. Conclusions Bibliographie
Encart 2: La première proposition de La mesure du cercle d'Archimède |
Pendant la première moitié du XVIIème siècle le problème de savoir si la quadrature du cercle est possible, à savoir s'il est possible de construire géométriquement un carré d'aire égale à celle d'un cercle donné, restait un problème ouvert dans l'agenda des mathématiciens [13].
Il est peut être surprenant de voir que face à la prudence montrée par exemple par Marin Mersenne (1588-1648) Note_1 , l'opinion de Descartes par rapport à la possibilité de la quadrature du cercle n'admet pas d'espace pour le doute. Ainsi, dans une lettre écrite en 1638, exposant à Mersenne quels genres de problèmes sont à placer hors de la géométrie, il juge de manière tranchante que la quadrature du cercle est impossible:
En examinant de plus près le problème, observons que la désignation d'un problème par le terme impossible demande une clarification. Des solutions à la quadrature du cercle avaient été produites depuis l'antiquité: ainsi, d'après le témoignage de Pappus dans le quatrième livre de la Collection mathématique, témoignage que Descartes connaissait dès ses débuts en mathématiques, les anciens géomètres avaient essayé de résoudre la quadrature du cercle par la construction de certaines courbes, telle que la quadratrice (dont l'introduction est généralement attribuée à Hippias, Voir Encart 1).
|
Figure 1
 Figure extraite deFedericus
Commandinus, editor. Pappus
Alexandrini
Mathematic
collectiones a Federico Commandino
[8] en bibliographie |
Par ailleurs, parmi les manuscrits de Descartes publiés avec le titre Excerpta ex MSS. R. Des-Cartes dans le volume Opuscola posthuma physica et mathematica (Amstelodami, ex typographiâ P. & J. Blaeu, 1701 1701) Note_3 , on peut trouver un fragment (le numéro 6), datable aux années 1625-1628, contenant une solution au problème de la quadrature du cercle, due à Descartes, et différente de celle de Pappus.
Dans cet article, je donnerai en premier lieu une reconstruction de la quadrature contenue dans le fragment 6 des Opuscula. Ensuite, je discuterai les raisons pour lesquelles Descartes n'accepta ni la solution que l'on trouve dans la Collection mathématique de Pappus, ni celle qu'il proposa lui même, comme légitimes par rapport à certains standards d'exactitude en force dans La Géométrie de 1637.
Il est à noter que Descartes ne reviendra jamais sur son texte sur la quadrature du cercle au cours de sa carrière. La première référence à cette démonstration est attribuable à Leonhard Euler (1707-1783), qui lui dédie un commentaire publié en 1763 dans les comptes rendus de l'académie de St Petersburgh: Annotationes in locum quendam Cartesii ad circuli quadraturam spectantem Note_4 .
Le fragment dans lequel Descartes présente sa quadrature est bref, et il peut être cité en entier:
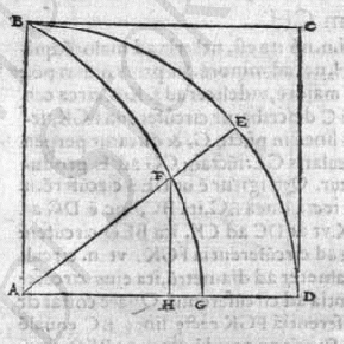
CIRCULI QUADRATIO. Ad quadrandum circulum nihil aptius invenio quam si dato quadrato bf adiungatur rectangulum cg comprehensum sub lineis ac & cb,quod sit aequale quartae parti precedentis; item rectangulum dh, factum ex lineis da, dc aequale quartae parti precedentis; & eodem modo rectangulum ei, atque alia infinita usque ad x; quae omnia simul aequanbantur tertiae parti quadrati bf. Et haec linea ax erit diameter circuli, cujus circonferentia aequalis est circumferentiae huius quadrati bf, est autem ac diameter circuli octagono, quadrato bf isoperimetro, inscripti; ad diameter circuli inscripti figurae 16 laterum, ae diameter circuli inscripti figurae 32 laterum, quadrato bf isoperimetrae, & sic in infinitum Note_5 .
LA QUADRATURE DU CERCLE. Pour carrer le cercle, je ne trouve rien de plus apte que, étant donné un carré bf, d'ajouter le rectangle cg délimité par les lignes ac et cb, égale à la quatrième partie du précédent; et ensuite le rectangle dh, formé par les segments da, dc égale à la quatrième partie du précédent, et de la même manière d'ajouter le rectangle ei, et ajouter ainsi d'autres rectangles jusqu'à l'infini, jusqu'à atteindre le point x. Tous ensemble, ils feront la troisième partie du carré bf. Et cette ligne ax sera le diamètre du cercle, dont la circonférence est égale au périmètre de ce carré bf. D'autre part, ac est le diamètre du cercle inscrit dans l'octagone isopérimètre au carré bf, ad le diamètre inscrit à la figure de 16 côtés, ae le diamètre du cercle inscrit dans la figure de 32 côtés, isopérimètre au carré bf; et ainsi à l'infini.
|
Figure 2
 |
Le texte se prête à être divisé en deux parties: dans la première, Descartes présente la construction d'une suite infinie des rectangles cg, dh, ei... tels que l'air de chacun soit égal à ¼ du précedent, et l'aire du premier à un quart d'un carré donné bf, pour en conclure que la somme de leurs aires équivaut à un tiers de l'aire de bf Note_6 . Dans la deuxième, il affirme que la suite de ces rectangles, construits comme sur la figure, détermine les diamètres des cercles inscrits dans les polygônes réguliers de 2n côtés (pour n ≥ 2), isopérimètres au carré de périmètre donné bf. De cette manière le segment maximal ax déterminera la mesure du diamètre du cercle inscrit dans la figure isopérimètre d'aire majeure: ax sera donc, le diamètre du cercle isopérimètre au carré bf Note_7.
Le problème de Descartes n'est ni celui de la quadrature du cercle, ni celui de la rectification de la circonférence, et il peut être resumé ainsi: étant donné la mesure de la circonférence, il est demandé de trouver son diamètre. Néanmoins, notons que Descartes donne au fragment le titre: "CIRCULI QUADRATIO" (quadrature du cercle). L'équivalence entre les deux résultats peut être établie sur la base de la première proposition du traité archimédien de la Mesure du cercle, connue parmi les mathématiciens du XVIIème siècle Note_8 , et qu'on pourra formuler comme suit (voir Encart 2):
Tout cercle a même aire que le triangle rectangle dont les côtés de l'angle droit ont pour longueurs respectives le rayon et la circonférence de ce cercle. Note_9 .
Sur la base de cette équivalence, si on connaît le rayon d'un cercle donné et la mesure de la circonférence, on peut construire une figure "rectiligne" d'aire égale à celle du cercle. Et comme le fragment de Descartes est censé offrir la mesure du rayon (ou du diamètre) à partir de celle de la circonférence, la quadrature du cercle peut être résolue par conséquent Note_10 .
Par contre, aucune indication dans le texte rend explicite la relation entre la construction des rectangles dont les aires sont en succession géométrique, et le fait que leurs bases forment la suite des diamètres, respectivement, du cercle et des polygones réguliers à 8, 16, 32, 64 côtés, sic in infinitum, isopérimètres au carré bf de départ.
Afin de donner une explication de la manière dont les deux moments de la démonstration cartésienne s'agencent, j'utiliserai le commentaire donné par Euler en 1763.
Au préalable Euler énonce un problème qui une fois résolu expliquera la relation entre la construction cartésienne des rectangles et la succession des diamètres des cercles inscrits dans les polygones aux côtés croissants en mesure double. Le problème peut être énoncé comme suit:
Étant donné un cercle inscrit dans un polygone régulier à n cotés, trouver un deuxième cercle, tel que, si l'on circonscrit autour de celui-ci un polygone à 2n côtés, les deux polygones seront isopérimètres.
|
Figure 3
 |
En procédant par une analyse dans le style de la géométrie ancienne, Euler suppose le problème résolu. Ainsi, il donne la première circonférence MNE. Le cercle a pour centre C et rayon CE. Le segment EP est la moitié du côté d'un polygone regulier circonscrit à MNE. Euler construit ensuite QF, moitié du côté du deuxième polygone aux côtés doubles du premier, et CF, le rayon du cercle à déterminer. On aura par conséquent QF = ½ EP, et, puisque le cercle inscrit dans le polygone à 2n côtés est plus grand que le cercle MNE, on aura CE < CF. Soit O le milieu du segment EP, on aura donc que QO est parallèle à EF. Enfin, soit V le point d'intersection entre le rayon CQ et le coté EP. Comme V tombe entre O et E, on aura EV < EO. Euler peut ensuite déduire les égalités :

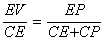
La première égalité peut être déduite de la similitude entre les triangles VCE et QFC, la deuxième demande un peu plus de travail Note_11 .
A partir de ces proportions, l'égalité suivante peut être facilement déduite: CF . EF = ¼ (CP² - CE²) = ¼ EP². Puisque FQ = ½ EP, et que

Par conséquent, le produit CF . EF sera égal à: ¼ (CP² - CE²). Le point F sera finalement défini de telle manière que le rectangle de côtés CF et EF, soit égal à un quart du carré construit sur EP.
Comme on a EO = QF = ½ EP, que l'angle QCF = ½ PCF, et que EP est perpendiculaire à CF, le point F pourra être trouvé comme projeté ortogonal sur CE de l'intersection entre la droite CV, bissectrice de l'angle PCE, et la médiatrice du segment EP.
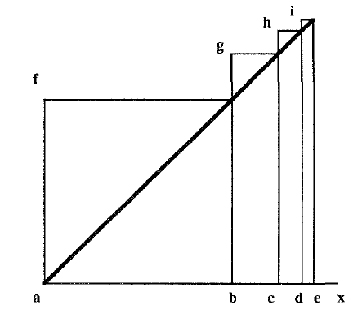
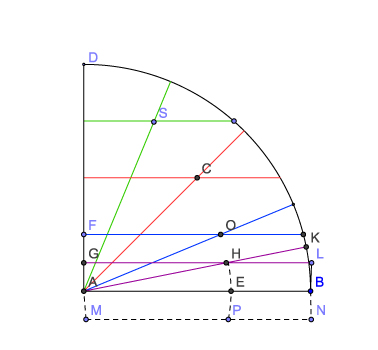
Une fois résolu le premier problème, Euler démontre la construction cartésienne. Soient CE, CF, CG, CH ... les rayons des cercles inscrits, respectivement, dans un carré, un octagone, un 16-gone, le 32-gone ... isopérimètres. Considérons ensuite les segments EP, FQ, GR, HS, respectivement, demi-côtés du carré, de l'octagone, du 16-gone... . On aura, sur la base du résultat précédent: FQ = ½ EP, GR = ½ FQ = ¼ EP , HS = ½ GR =¼ FQ = 1⁄8 EP, ... ...
|
Figure 4
 |
On sait aussi, du problème précédent, que: CF . EF = ¼ EP² = FQ². De la même manière, on aura:
CG . FG = ¼ FQ² = ¼ CF. EF = GR² = 1⁄16 EP²
CH . GH = ¼ GR² = ¼ CG . FG = HS² = 1⁄32 EP² , etc.
En doublant les demi-côtés des polygones, nous pourrons définir une succession de points F, G, H, I ... tels que les rectangles construits de côtés CG, FG et CH, GH, etc. (que je noterai r(CG, FG), r(CH, GH), etc.) seront égaux à un quart des carrés respectifs de côté EP, QF, etc. (que je noterai q(EP), q(QF), etc.). De cette manière on aura:
r(CF, EF= ¼ EP²
r(CG, FG) = 1⁄16 EP²
r(CH, GH) = 1⁄32 EP²
De cette manière, la somme des rectangles correspondra à la limite de la série géométrique de raison ¼ , pour n tendant à l'infini, multipliée par l'aire du carré de côté EP: donc 1⁄3 EP², comme dans la construction cartésienne. Notons aussi que la solution du problème précédent donne une manière de construire la succession des points F, G, H, I ... à la règle et au compas. Le point Q est obtenu par intersection entre la médiatrice de EP et la bissectrice de PCE. Le point R est obtenu par intersection entre la médiatrice de QF (moitié de EP) et la bissectrice de l'angle QCE (la moitié de PCE), etc. Ainsi chaque point est construit par intersection entre la médiatrice d'un segment de longueur PE / 2n et la bissectrice d'un angle de mesure PCE / 2n .
Je remarque que Euler tient à séparer le commentaire de la proposition cartésienne de ses développements analytiques, données dans une deuxième partie du commentaire, et que sa reconstruction du passage de Descartes ne présuppose aucune connaissance technique qui ne fusse disponible à Descartes lui-même. Il est donc possible que ce dernier ait suivi cette voie pour construire la succession de rectangles cg, dh, ei ...
Pour ce qui concerne l'ordre suivi par Descartes dans l'exposition de ses résultats, Pierre Costabel a voulu voir dans "la préférence explicite (...) pour la considération des aires le souci de justifier l'existence de la limite Cx avant même de passer à l'interprétation de cette limite comme mesure liée à un polygone régulier" Note_12 . Bien que les éléments pour conclure que Descartes puisse avoir abouti, à un certain moment de sa carrière, à une notion de passage à la limite sont insuffisants, on peut faire l'hypothèse, suggerée par Whiteside Note_13 , qu'il se soit servi de la série de raison ¼ comme série de comparaison pour tester la convergence de la méthode des isopérimètres Note_14 . Selon cette hypothèse, Descartes aurait pu raisonner comme il suit: si l'aire de la figure formée par le carré bf et la succession des rectangles est égale à une quantité finie (notamment, 4⁄3 bf), sa base Cx sera égale à une quantité finie aussi (voir Figure 2). Comme on sait que la première condition vaut, on aura aussi la seconde, et donc, on pourra conclure que la succession des apothèmes tend vers la limite Cx, diamètre du cercle isopérimètre au carré de départ.
La solution d'un problème ainsi que son acceptation à l'intérieur d'une communauté mathématique ne dépendent pas seulement de l'absence d'erreurs dans le calcul ou de l'absence d'arguments fallacieux dans la structure logico argumentative: souvent, l'emploi de procédures de résolution dépend de leur recevabilité par rapport à des standards extra-mathématiques Note_15 . A ce propos, Henk Bos a montré que parmi les mathématiciens, entre XVIème et XVIIème siècle, un ensemble de critères, qu'il appelle exactitude géométrique, a été au centre d'un important débât. Les points principaux de ce débât concernaient les moyens nécessaires et suffisants pour considérer un objet comme connu, accepter ou refuser une procédure de construction d'un object géométrique ou la solution d'un problème de géométrie Note_16.
Dans les mathématiques du XVIIème siècle, le problème de l'exactitude géométrique suit une double articulation [18]: il consisterait premièrement dans la fixation de procédures admissibles pour résoudre des problèmes, qui, tout en étant formulées par l'emploi de concepts introduits dans les livres géométriques des Eléments, résistent à une solution par la règle et le compas (comme la quadrature du cercle), et deuxièmement dans la détermination des conditions d'admissibilité de ces procédures.
Dans La Géométrie de Descartes, en particulier, les deux moments de la question sont entrelacés. Comme la solution d'un problème mathématique est conçue par celui-ci en termes de construction d'un point ou d'un lieu par des courbes, sa réponse au problème de l'exactitude consiste dans la formulation d'un critère de recevabilité des courbes, à son tour fondé sur des contraintes au niveau de leur construction. Le passage suivant illustre bien les considérations précédentes:
La notion de constructibilité que Descartes déploie ici pourrait etre interprétée comme la tentative de prendre les clauses constructives fixées dans les postulats d'Euclide comme base pour des constructions récursives Note_18 , aboutissant à d'autres courbes, dont le caractère effectif ne saurait pas être mis en doute. Bien évidemment, pour Descartes aussi, parmi les courbes reçues en géométrie on doit compter cercles et droites, construits à la règle et au compas. Ensuite, par ces mêmes constructions à la règle et au compas, on peut obtenir certaines configurations de droites et de cercles, qui formeront des sytèmes articulés. Si on soumet ces systèmes à des mouvements appropriés, certains de leurs points, forcés à se déplacer sur des trajectoires univoques, traceront de nouvelles courbes. Ces courbes composées seront recevables en géométrie. A leur tour, seront recevables toutes les courbes engendrées par des systèmes articulés et soumis à des mouvements qui combinent les courbes précédemment construites entre elles et avec cercles et droites. On appelera un tel critère de recevabilité, pour souligner sa continuité avec les clauses constructives euclidiennes, critère par règle et compas reitérés [17].
Mais qu'est ce que signifie être soumis à des mouvements appropriés? Une caractérisation pourrait être la suivante: un système articulé est soumis à un mouvement approprié si les propriétés géométriques de la courbe tracée par ce système ne dépendent pas des caractéristiques cinématiques du mouvement. Ainsi, la construction de la quadratrice présentée par Pappus ne pourra pas garantir l'admissibilité de cette courbe en géométrie, parce que la trajectoire du point qui trace la courbe dépend de la vitesse des axes mouvants. Il n'est donc pas étonnant que sur cette base, Descartes ne reçoive pas comme acceptable la quadrature du cercle résolue par la quadratrice.
A la différence de cette construction, pourtant, la procédure appliquée par Descartes pour sa quadrature ne demande l'application d'aucune courbe, à part les droites et les arcs de cercle impliqués dans la construction des rectangles (nous avons en fait montré que chacun d'eux peut être obtenu par des bisections successives de segments et d'angles). Il s'agit donc d'une procédure euclidienne, à la règle et au compas. Il est vrai qu'elle pourrait être jugé approximée, et donc non exacte. Néanmoins cette conclusion, bien que prima facie raisonnable, invoque une justification: pour quelle raison cette procédure ne se conforme pas au critère de recevabilité précédemment exposé?
D'autre part, tandis que ce critère établit qu'une courbe est recevable s'il existe un système articulé d'engendrement qui obéit à certains réquisits, Descartes imagine et expose, toujours dans La Géométrie, deux autres systèmes d'engendrement de courbes: la construction point par point, et celle par des cordes.
Dans cet article, je me limiterai à considérer le premier type de construction, qui est introduit premièrement en relation aux problèmes indeterminés, dans lesquels un lieu géométrique est à déterminer par des conditions, exprimées par une équation, que tous les points d'un lieu doivent satisfaire. La solution d'un problème indeterminée peut donc être construite comme Descartes l'explique:
..on peut prendre à discretion l'une des deux quantités inconnues x ou y et chercher l'autre par cete Equation .. mesme prenant successivement infinies diverses grandeurs pour la ligne y on en trouvera aussi innies pour la ligne x, et ainsi on aura une infinité de divers poins...par les moyens desquels on décrira la ligne courbe demandée... ([10], p. 313).
En d'autres termes, une construction point par point d'un lieu est obtenue en prenant un nombre arbitraire de valeurs pour l'une des deux inconnues (par exemple, y), pour se ramener ainsi à une équation à une seule inconnue (par exemple, x) qui peut être résolue géométriquement, selon les méthodes illustrées au premier et au troisième livre. Par ce processus de construction on peut déterminer un réseau formé par un nombre arbitraire de points distribués sur une courbe.
Toujours au deuxième livre, Descartes présente la construction point par point comme méthode de construction générale des courbes, sans référence au contexte du problème de Pappus. Le cas traité dans La Géométrie, est celui de la construction des ovales. Parmi les différentes manière de construire ces courbes, je décrirai la suivante:
|
Figure 5
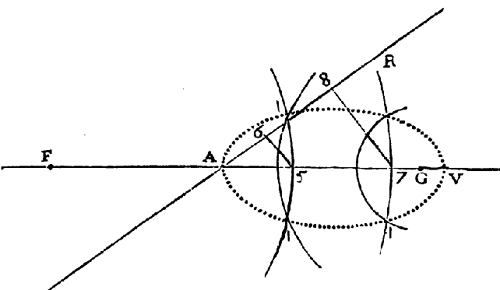 Figure extraite de La
Géométrie, Descartes, [11]
p. 352
|
Soient FG et AR deux lignes qui se croisent en A selon un angle donné. A gît entre F et G, de manière que le rapport entre AF et AG soit donné aussi (pris à discretion, observe Descartes). On pose ensuite AR = AG. Prenons le point 5, arbitrairement choisi sur AG, et traçons le cercle de centre F et rayon F5. Traçons le segment 56, perpendiculaire à AR, et ensuite le cercle de centre G et rayon R6. Les deux points d'intersection des deux cercles de rayon respectifs F5 et R6 appartiennent à l'ovale. Réitérant la même construction, en partant d'autres points arbitrairement choisis sur AG (comme 7), on peut déterminer un réseau formé par un nombre arbitraire de points distribués sur la même courbe. Ce n'est pas du tout immédiat de considérer ce procédé de construction autant exact et précis qu'un procédé de construction obtenu par un système articulé, puisque il faut vérifier, dans le cas des constructions point par point, que tous les points de la courbe ont été ainsi construits. De plus, lorsqu'il traita de ce type de construction, Descartes devait avoir à l'esprit les remarques de certains mathématiciens Note_19 qui avaient critiqué cette façon de construire une courbe parce qu'elle n'offre pas la courbe dans sa totalité, au contraire d'un acte de mouvement, qui donnerait la totalité des points d'une courbe sans laisser de trous dans son tracé.
Sur quel fondement Descartes s'appuie-t-il donc pour déduire la non recevabilité de la procédure de quadrature à partir de sa solution au problème de l'exactitude et en même temps la recevabilité de sa procédure de construction point par point des courbes?
Pour répondre à cette question, je commencerai par montrer qu'en traitant des constructions point par point, Descartes distingue deux façons de construire une courbe:
...ayant expliqué la façon de trouver une infinité de poins par ou elles [les courbes] passent, je pense avoir assés donné les moyens de les décrire. Mesme, il est a propos de remarquer qu il y a grande diference entre cete façon de trouver plusieurs poins pour tracer une ligne courbe, et celle dont on se sert pour la spirale, et ses semblables. Car par [cete] dernière on ne trouve pas indifféremment tous les points de la ligne qu'on cherche, mais seulement ceux qui peuvent être determinés par quelque mesure plus simple, que celle qui est requise pour la composer, et ainsi a proprement parler, on ne trouve pas un de ses points, c'est à dire pas un de ceux qui luy sont tellement propres qu'ils ne puissent estre trouvés que par elle Note_20 .
La première façon, dont la construction des ovales est un exemple permet de construire indifféremment tous les points: Henk Bos parle d'une méthode générique Note_21 ; alors que la deuxième n'offre qu'un sous-ensemble des points de la courbe, obtenus par des moyens plus simples que ceux demandés pour sa construction. Cette deuxième façon est appelée méthode spécifique, toujours par Henk Bos Note_22 .
Descartes, tout en faisant allusion à une
méthode dont on se sert pour
la spirale et ses
semblables, ne donne aucun exemple de
construction spécifique. Par ailleurs, de nombreuses
études Note_23
ont montré qu'il avait probablement à l'esprit la
construction point par point de la quadratrice, offerte par
Christophorus Clavius (1538-1612) dans le livre VI de ses Commentaria
aux d'Euclide, publiés en 1598 (le texte
spécifique
fut reédité dans la ElémentsGeometria
practica de 1604). Voici comment la construction de la
quadratrice est décrite:
quare nos Geometrice eandem lineam Quadratricem describemus hoc modo. Arcus BD in quotius partes aequales dividatur, & latus utrum AD, BC in totidem aequales partes. facillima divisio erit, si et arcus DB et utrumque latus AD, BC secetur primum bifariam, deinde utraque semissis iterum bifariam, etc., ita deinceps, quantum libuerit. Quo autem plures existerint divisiones, eo accuratius linea describebitur... Note_24 ([7], p. 321).
|
Figure 6
 |
Les intersections des segments ainsi tracés formeront un réseau de points appartenant à une quadratrice. Dans ce passage, Clavius déclare offrir une construction géométrique de la quadratrice plus précise que celle présentée dans la Collection de Pappus. Il se refère, en particulier, à l'une des deux objections relatées par Pappus même et attribuées à Sporus: selon celle ci, le point d'intersection entre la quadratrice et l'axe ne peut pas être construit, puisque les deux segments en mouvement coincideront sur l'axe horizontal, et le tracé de la courbe cesserait avant de rencontrer celui-ci Note_25 .
D'après Clavius, donc, cette construction offrirait le point d'intersection entre quadratrice et axe, sans besoin de recourir à la génération de la quadratrice par combinaisons de surfaces plectoides Note_26 , présentée dans la Collection Mathématique Note_27 . Cependant, pour construire le point d'intersection, Clavius doit recourir à une astuce. Il demande de continuer la procédure de divisions successives de l'arc et du segment jusqu'à obtenir le segment AF et l'arc BK. Ensuite, Clavius demande de construire les segments BL, BN, AM de longueur égale à AG, et de tracer les segments MN et GL. L'intersection entre les segments GL et AK donnera alors le point H, appartenant par construction à la quadratrice. Clavius demande alors de tracer le segment MP égal à GH, et ensuite, de prolonger la quadratrice jusqu'au point P, en dessous de la base AB, par la même procédure: elle coupera la base dans le point E recherché (voir Figure 6). Clavius ajoute alors que, si on a construit les segments GH, AE, MP très proches l'un à l'autre, ce point E pourra être trouvé par l'intersection entre l'arc de cercle HP (de centre A) et le segment AB. Notons que cette procédure ne construit pas le point E, mais un point assez proche. Tout en étant conscient de ce fait, Clavius considérait que cette construction approchée détermine le point de la quadratrice lorsque l'erreur n'est pas perceptible par les sens:
... sed quia punctum E, in latere AB, invenire geometrice non potest, cum ibi omnis sectio rectarum cesset: ut illud sine notabili errore, quiscilicet sub sensum cadat, reperiamur ... Note_28 .
En faveur de l'hypothèse qui considère cette discussion à la base de la distinction faite dans La Géométrie entre deux procédures de construction point par point, commençons à noter que l'étude de Clavius laissa une forte empreinte sur Descartes bien avant la composition du traité de 1637 Note_29 .
Autour de 1614-1615, Isaac Beeckman (1588-1637), avec lequel Descartes collabora entre 1618 et 1619, fait référence dans son journal au même texte de Clavius sur la quadratrice en relation au problème pratique de construction de conduits d'eau d'inclinaison croissante. Tout particulièrement, Beeckman montre que la meilleure façon de disposer des tuyaux est telle que leurs extrémités appartiennent à une quadratrice, qu'il construit par la méthode de Clavius Note_30 .
Ensuite, une lettre de 1629 adressée par Descartes à Mersenne témoigne que à cette époque le mathématicien connaissait certainement la construction point par point de la quadratrice donnée par Clavius:
... la ligne helice que vous ne m'avies point nommee & qui n'est pas une ligne plus receue en geometrie que celle qu'on appelle Quadratricem, pource qu'elle sert à carrer le cercle & mesme a diviser l'angle en toutes sortes de parties esgales, aussy bien que celle cy & a beaucoup d'autres usages que vous pourrés voir dans les Elemans d'Euclide commantés par Clavius. Car, encore qu'on puisse trouver une infinité de points par ou passe l'helice & la quadratrice; toutefois on ne peut pas trouver geometriquement aucun des poins qui sont necessaires pour les effaits desirés tant de l'une et tant de l'autre...
Ces deux évidences sont importantes afin de montrer que Descartes connaissait donc très certainement l'étude de Clavius lorsqu'il commenta, au deuxième livre de La Géométrie, les constructions point par point spécifiques. Notons qu'en 1629 Descartes écrit que parmi les points qui ne peuvent pas être trouvés géométriquement, il y a ceux nécéssaires pour les effets désirés. Comme la quadrature du cercle peut être incluse parmi les effets désirés découlants de l'emploi de la quadratrice, on peut inférer que Descartes ait voulu souligner que le point E d'intersection entre quadratrice et axe, requis afin d'établir la proportion qui donne la quadrature du cercle, ne saurait pas être constructible par la procédure de construction employée par Clavius.
Observons aussi que les deux constructions de Clavius sont étroitement liées au fragment cartésien sur la quadrature du cercle. Il suffit de les comparer pour remarquer que la procédure de construction qui donne les points de la quadratrice dans la construction offerte par Clavius donne aussi les points P, Q, R... , à partir desquels on peut construire par simple projection orthogonale: E, F, G..., bases des rectangles dont la mesure de l'aire est en progression géométrique de raison un quart. Dans les deux cas, en fait, les points sont obtenus par bissections successives d'un angle droit et de l'un des côtés du carré de départ.

Pourtant, le point x dans la construction cartésienne (voir Figure 2) est déterminé différemment de son analogue E dans celle de Clavius. Ce dernier détermine E en construisant, par l'application de la procédure expliquée plus haut, un point qui s'approche tellement du premier point que la distance entre les deux tombe en dessous de notre seuil de perception. Au contraire, dans le fragment de Descartes la procédure de construction du point x, diamètre du cercle de périmètre donné, ne s'arrête pas à un seuil physique de perception: la distance entre le point x et le point qui donne l'apothème du polygone régulier à 2n côtés peut toujours être raccourcie: il suffit, en théorie, de réitérer la même procédure pour obtenir l'apothème du polygone dont le nombre de côtés est le double du précédent. Pour cette raison, la quadrature du cercle cartésienne, à la différence de la construction de la quadratrice de Clavius, se fonde sur une procédure d'approximation infinie.
Derrière ces conclusions différentes, nous pouvons percevoir deux conceptions différentes de l'exactitude en géométrie. Pour Clavius, il y aurait un parallèle entre exactitude géométrique et précision pratique. Même si ce parallèle n'est jamais éclairci, on peut conclure à partir des exemples discutés que la précision obtenue dans les méthodes pratiques de dessin et de construction serait un critère suffisant pour décider de l'exactitude théorique d'un procédé ou d'une construction.
Au contraire, la notion d'exactitude que Descartes met en place, au moins dans La Géométrie de 1637, semble avoir une relation plus atténuée avec les méthodes de géométrie pratique. On peut le remarquer dans le cas des systèmes de tracement de courbes, qui bien que réalisables en pratique, restent des systèmes imaginés, mais aussi dans la distinction entre constructions point par point générique ou spécifique.
En fait, le caractère infini du procédé d'approximation qui figure dans le fragment sur la quadrature du cercle est fondamental pour saisir la distinction entre les deux façons de construire une courbe point par point. En revenant à l'exemple des ovales (voir Figure 5), je fais remarquer que dans ce cas chaque point du lieu est obtenu comme intersection entre deux courbes géométriques, déterminées à leur tour par l'application d'une suite finie de constructions exactes, à partir d'un point choisi arbitrairement sur une droite: cette caractéristique est généralisable à toute construction point par point générique.
Au contraire, la solution cartésienne à la quadrature du cercle montre, à cause de sa quasi-équivalence avec la construction point par point de la quadratrice donnée par Clavius, que le point E, intersection entre cette courbe et la droite AB, ne peut pas être construit en un nombre fini de pas par la même procédure qui donne les points C, O, H (Cf. Figure 6). Par conséquent, cette méthode, tout en trouvant un nombre infini de points de la quadratrice, ne trouve pas, comme Descartes le remarque, et contre l'opinion de Clavius, ce point E, nécessaire pour les effets désirés. D'où le caractère spécifique de cette construction point par point de la quadratrice.
Pour conclure, revenons aux deux questions soulevées plus haut: sur quel critère Descartes s'appuie-t-il pour déduire la non recevabilité de la procédure de quadrature, et, en même temps, la recevabilité de la procédure de construction point par point générique des courbes?
Revenons au modèle d'exactitude introduit au § 3. Rappelons qu'une procédure de construction d'une courbe a été définie exacte si: (i) elle est une procédure à la règle et au compas, ou bien, (ii) elle se fonde sur des sytèmes articulés et soumis à des mouvements, qui combinent deux segments et un cercle pour construire de manière appropriée de nouvelles courbes non constructibles à la règle et au compas, ou encore (iii) elle se fonde sur des systèmes articulés et soumis à des mouvements qui combinent les courbes précédemment construites entre elles et avec des cercles et des segments.
On pourra préciser la solution cartésienne au problème de l'exactitude, en spécifiant, qu'un objet est déterminé par une procédure exacte si: (i) il s'agit d'une courbe engendrée par règle et compas réitérés; (ii) dans le cas d'un point appartenant à un lieu, s'il est construit par intersection entre deux courbes construites par règle et compas réitérés, à partir d'un point arbitrairement choisi sur une droite. Cette dernière condition est équivalente à la suivante: un point est déterminé exactement s'il peut être relié par une chaîne finie de constructions par règle et compas réitérés à un point arbitrairement choisi (comme dans l'exemple des ovales).
Sur la base de (i) et de (ii) on peut conclure que:
si les points d'un lieu sont construits par une procédure point par point générique, alors ils sont détérminés exactement Note_31 .
Dans le fragment sur la quadrature du cercle, le point x qui donne le diamètre du cercle isopérimètre au carré donné n'est pas déterminé exactement par la procédure de bissection successive du segment EP et de l'angle PCF (voir Figure 4).
Il en est de même pour le point d'intersection entre quadratrice et base dans la construction point par point donnée par Clavius.
On pourra donc conclure que, par rapport à la solution cartésienne au problème de l'exactitude, comprenant un critère de recevabilité des courbes ainsi qu'un critère de détermination exacte d'un objet, ni la solution à la quadrature du cercle présentée par Pappus, ni celle offerte par Descartes dans le fragment 6 des Opuscula Posthuma seront recevables comme solutions géométriques du problème.
Notons que cette conclusion n'explique pas pourquoi Descartes considérait ce problème impossible, mais elle contribue à éclairer la signification du terme dans le contexte de la pratique cartésienne de solution de problèmes. Impossibilité donc, non pas comme absence de solution tout court, mais comme absence de solution conforme à un idéal d'exactitude, et donc, de géométricité.