Encart 1: Sur la démonstration de Pappus

    Pour résoudre le problème de la quadrature du cercle, à savoir, de la construction d'un carré ayant même aire que celle d'un cercle donné, les géomètres de la Grèce ancienne ont inventé des courbes spéciales, telles que la spirale et la quadratrice. La construction et les propriétés des deux courbes sont discutées par Pappus au quatrième livre de la Collection mathématique. Dans cet encart, je me baserai sur le texte de Pappus pour montrer comment la quadratrice peut effectuer la quadrature du cercle.

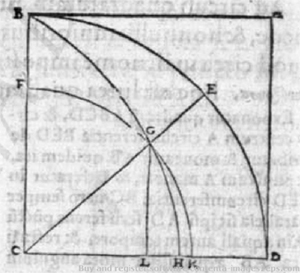
   Cette courbe, observe Pappus, peut être obtenue comme la trajectoire du point B, intersection entre le segment CB qui se déplace en rotation autour du centre C d'un cercle, et du segment BA, qui en même temps se déplace verticalement à même vitesse. Supposons donné le cercle de rayon CD, dont on veut construire le carré d'aire équivalente. En prenant CD et CB comme axes, on tracera, par le mécanisme décrit, une quadratrice qui intercepte CD en H. Parmi les propriétés de cette courbe remarquons la suivante: si un rayon CE quelconque est tracé à partir du centre, il interceptera la quadratrice en un point G tel que, si L est le projeté orthogonal de G sur le côté CD du carré, on aura la proportion suivante:  CB : GL = arc(BD) : arc(ED) [16].

Afin d'obtenir la quadrature du cercle à partir de la quadratrice, Pappus commence par démontrer la proportion suivante: arc(BD) : CD = CD : CH.

   La démonstration est donnée par l'absurde, selon le schéma suivant. On suppose, avec Pappus, que arc(BD) : CD ≠ CD : CH. Donc, la quadratrice doit couper le segment CD en un autre point K qui satisfait la relation précédente. On aura par conséquent soit  CK  > CH, soit CK < CH, et arc(BD) : CD = CD : CK.

   Puisque ces deux cas mènent tous les deux à une contradiction, la proposition est démontrée. Précisons le premier cas (le deuxième peut être traité de manière analogue). Soit donc CK plus grand que CH; avec le centre C et le rayon CK, on trace l'arc de cercle KGF, où G est le point d'intersection du cercle et de la quadratrice, et F un point sur CB. On demande ensuite de joindre C avec G, et de prolonger le segment en E, point de la circonférence de rayon CB (=CD).

Figure extraite de Federicus Commandinus, editor. Pappus Alexandrini Mathematic collectiones a Federico Commandino ([8] en bibliographie)

Par hypothèse, on a que: CB (= CD) : CK = arc(DEB) : CB

En même temps la proportion suivante vaut: CB : CK = arc(DEB) : arc(KGF) *.

Finalement, on peut déduire, des proportions précédentes: arc(KGF) = CB. 

De même on aura:  CB : GL = arc(KGF) : arc(GK) . Puisque on a prouvé que arc(KGF) = CB , on peut ainsi conclure:  GL = arc(GK), qui est absurde. Une conclusion identique est obtenue si l'on suppose CK < CH.

Comme les longueurs de CB et CH sont connues, la longueur de l'arc BD pourra être déterminée. En multipliant par 4 les membres de l'égalité arc(BD) : CD = CD : CH , on obtiendra la mesure de la circonférence, à savoir, sa rectification. Pour passer de la rectification de la circonférence à la quadrature du cercle on se servira d'un théorème démontré par Archimède dans la Mesure du cercle (voir Encart 2)