Encart 1: La première proposition de La mesure du cercle d'Archimède

J'ai cité l'énoncé de la proposition 1 du traité d'Archimède:

Tout cercle a même aire que le triangle rectangle dont les côtés de l'angle droit ont pour longueurs respectives le rayon et la circonférence de ce cercle.

Je donnerai dans la suite la démonstration de cette proposition, telle qu'elle se trouve dans le texte d'Archimède. Il s'agit d'un bel exemple d'emploi de la méthode d'exhaustion.

L'auteur considère avant tout le cercle donné Γ, passant par A, B, C, D, et le triangle K, et procède comme suit. Si on suppose l'aire S( Γ) du cercle inégale à celle S(K) du triangle, S( Γ) doit être soit plus grand soit plus petite que S(K) . On considère la première possibilité, à savoir, que le cercle est plus grand que K.

On pourra donc écrire, pour simplifier, en notation moderne: S( Γ) > S(K)

Ensuite, Archimède demande d'inscrire dans le cercle un carré, puis un octagone, puis un polygone de 16 côtés, etc... obtenus par bissections des segments précédents, jusqu'à obtenir un polygone régulier P tel que la différence entre l'aire du cercle et la sienne soit moindre que la différence entre l'aire du cercle et l'aire de K. Ce résultat peut être transcrit ainsi:

S( Γ) - S(P) < S( Γ) - S(K)

L'aire du polygone sera donc plus grande que l'aire du triangle K: S( P) > S(K). En même temps, le périmètre du polygone sera plus petit que la circonférence du cercle, et son apothème inférieur au rayon. Mais on sait que l'aire d'un polygone peut être calculée comme le démi-produit du périmètre fois l'apothème. Or, comme l'apothème de P et son périmètre sont inférieurs au rayon et à la circonférence du cercle, respectivement, son aire sera nécessairement inférieure à l'aire du triangle rectangle K, qui a pour côté deux segments de même longueur que le rayon et la circonférence du cercle, respectivement. Par cette voie, on obtient une contradiction.

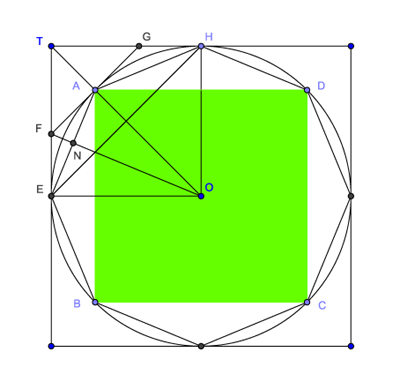
Archimède peut donc explorer l'autre branche de l'alternative : S( Γ) < S(K) . On pourra ainsi exinscrire un carré au cercle Γ . Soit T le point de rencontre entre deux côtés adjacents, et tangents à la circonférence aux points E et H. On bissectera l'arc EH en A, et par A, on tracera la tangente FG au cercle Γ. L'angle TAG sera droit, et on obtiendra les inégalités suivantes:  TG > GA > GH.. Archimède peut ensuite démontrer que l'aire la partie du triangle TEH qui gît en dehors du cercle est inférieure à la moitié de l'aire du triangle TEH. De la même manière, si on divise l'arc AH et on trace la tangente au point de bissection, cette droite retranchera de GAH une aire supérieure à la moitié. En continuant ce processus, on peut ainsi arriver au polygone P', tel que:

S(P') - S( Γ) < S( K) - S( Γ)

On aura ainsi  S(P') < S( K). Mais, puisque le périmètre du polygone est plus grand que la circonférence du cercle, et que son apothème est égal au rayon du cercle, il s'ensuit, comme pour le cas précédent, que l'aire du polygone dépasse celle du triangle K. On obtient ainsi une nouvelle contradiction.