Le processus d'abstraction dans le développement des premières théories de la mesure

Émile Borel (1871-1956) fut le premier mathématicien à définir, avec succès, la mesure non pas comme un calcul, mais comme une liste de propriétés. Cette nouvelle façon de définir la notion de mesure s'opposa alors aux notions de P-mesure et de J-mesure proposées respectivement par Peano (1887) et par Jordan (1892) [1] .

Après avoir présenté les recherches de ces trois mathématiciens, nous étudierons le processus d'abstraction réfléchissante développé par Jean Piaget. Nous obtiendrons ainsi que le changement d'attention de la part du sujet, la reconstruction de la notion en choisissant des propriétés constitutives et la réorganisation du savoir mathématique sont des caractéristiques du processus d'abstraction. En fait, pour le cas de la notion de mesure, le changement d'attention permet de passer d'un calcul aux propriétés utilisées dans ce calcul. Or, comme nous le verrons en analysant les travaux de Peano et de Jordan, ce passage n'est pas suffisant pour faire une abstraction. Nous comparerons nos résultats aux recherches d'Aline Robert et de Jean Cavaillès.

Ensuite, nous nous intéresserons à l'intégration que fit Lebesgue en liant la théorie de la mesure à la théorie de l'intégrale. Nous pourrons aussi, en utilisant ces travaux, comparer le processus d'abstraction au processus de généralisation.

Finalement, nous montrerons que les processus d'abstraction et de généralisation ont été nécessaires pour développer les notions de la théorie contemporaine de la mesure. Nous remarquerons alors qu'une abstraction change la compréhension de la notion, ce qui n'est pas nécessairement le cas pour une généralisation. De plus, ce passage à la version contemporaine mettra en évidence une autre caractéristique du processus d'abstraction, la spécialisation des notions.

2. Les versions calculatoires de Peano et de Jordan

Nous retrouvons, dans les travaux de Giuseppe Peano (1858-1923) et Camille Jordan (1838-1922), deux versions calculatoires d'une mesure. Les recherches de Peano ne furent pas connues de Jordan, mais ces deux mathématiciens furent les premiers à lier, avec succès, une théorie de la mesure avec la théorie de l'intégrale.

Peano présenta ce lien dans un chapitre, intitulé Grandeurs géométriques, du livre Les applications géométriques du calcul infinitésimal publié en 1887. En fait, pour calculer l'aire d'un ensemble de points du plan, il utilisa deux suites de figures géométriques euclidiennes. La définition suivante fut proposée :

Définition (La P-mesure d'un ensemble) [D'après Peano 1887]

Soit E un ensemble de points de R². Alors E est P-mesurable si les deux aires suivantes sont égales :

1) L'aire intérieure est la borne supérieure des aires des polygones qui sont intérieurs à E.

2) L'aire extérieure est la borne inférieure des aires des polygones qui contiennent E dans leur intérieur.

Il présenta aussi des définitions pour R et R³ en utilisant respectivement des segments linéaires et des prismes ou des solides décomposables en prismes. Or, cette approche (géométrique) le contraint à se limiter aux ensembles de points de la ligne, du plan ou de l'espace. Par contre, il voulut généraliser sa définition de P-mesure en remplaçant les suites de polygones par des suites de magnitudes géométriques principales, mais nous y reviendrons dans la section 5.

Jordan n'eut pas ce problème d'interprétation dans Rⁿ, car il proposa, dans son article Remarques sur les intégrales définies de 1892, un quadrillage du plan ou, plus généralement, un découpage de Rⁿ en n-cellules. Ce quadrillage lui permit donc d'utiliser deux suites de carrés (ou n-cellules dans le cas de Rⁿ) : ceux qui sont strictement à l'intérieur de l'ensemble (Figure 1a) et ceux qui rencontrent l'ensemble (Figure 1b). On peut ainsi calculer l'aire (ou le volume dans le cas de Rⁿ) et obtenir une approximation de l'aire intérieure et extérieure de l'ensemble.

Figure 1 : Les carrés utilisés par Jordan Figure 1a Les carrés qui sont à l'intérieur de E Figure 1b Les carrés qui rencontre E

De plus, en diminuant la longueur du côté r (comme dans la Figure 2 en passant de r₁ à r₂), on obtient des valeurs plus précises d'aire intérieure et en passant à la limite, la valeur de l'aire intérieure ou ce que Jordan appelle, l'étendue intérieure de l'ensemble.

Figure 2 : La  suite Pk utilisée dans l'étendue intérieure     Quadrillage initial Quadrillage plus fin

La définition proposée par Jordan est donc la suivante :

Définition (Les étendues intérieure et extérieure et la J-mesure) [D'après Jordan, 1892]

Soit E un ensemble borné de Rⁿ. Alors E est J-mesurable si l'étendue intérieure et l'étendue extérieure sont égales :

1) Soit la suite de n-cellules 

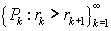
telle que contient toutes les n-cellules intérieures à E pour tout k (Figure 2). Alors, l'étendue intérieure de E se calcule comme suit :

,

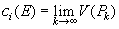où V(P_k) est le volume de la n-cellule.

2) Soit la suite de n-cellules 

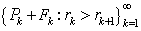
telle que F_k contient toutes les n-cellules ayant au moins un point de la frontière. Alors, l'étendue extérieure de E se calcule comme suit :

, 

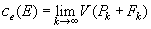où V(P_k+F_k) est le volume des deux n-cellules.

Contrairement aux travaux de Peano de 1887, Jordan présenta des preuves de ses résultats. Il démontra [2] que l'étendue intérieure et l'étendue extérieure d'un ensemble borné existent toujours et que la J-mesure satisfait les propriétés suivantes :

Théorème (Certaines propriétés de la J-étendue) [D'après Jordan, 1892]

1) Soit E un ensemble borné et soit E'⊂ E. Alors   c_e(E') ≤  c_i(E).

2) Soit 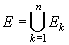     ,     avec n ensembles E_k disjoints deux à deux et bornés. Alors  

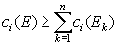           et          

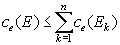
3) Soit E un ensemble borné et soit une suite   de décompositions de Rⁿ en ensembles J-mesurables disjoints deux à deux dont dont la largeur du quadrillage est r. Alors 

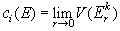   avec les     .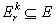  

   De plus, E est J-mesurable si      

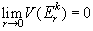        avec 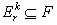          où F est la frontière de E.

Pour démontrer ces propriétés, Jordan utilisa la même idée que celle utilisée pour démontrer l'existence des étendues intérieures et extérieures. Il a donc recherché la portée maximale de la preuve initiale. De plus, ces propriétés lui permirent d'étendre l'extension de la notion de J-mesure, c'est-à-dire de trouver le plus grand nombre d'ensembles mesurables au sens de Jordan. Cette quête de la portée maximale d'une preuve ou d'une notion est une caractéristique du processus de généralisation et non du processus d'abstraction, puisqu'on s'intéresse à augmenter l'extension de la preuve et non à trouver des propriétés qui sont effectivement à l'œuvre dans la preuve. Nous reviendrons à cette distinction.

3. Les travaux de Borel de 1898

Nous avons vu que Peano et Jordan ont défini une façon de calculer la P-mesure ou la J-mesure d'un ensemble de points. Borel quittera cette version calculatoire pour s'intéresser aux propriétés de la notion. En effet, il publia un livre en 1898 intitulé Leçon sur la théorie des fonctions dans lequel il consacra un chapitre sur les ensembles mesurables et un autre sur la théorie de ensembles. Il proposa la définition suivante qui inclut une propriété très importante pour la suite de la théorie de la mesure, la sigma-additivité (propriété B2) :

Définition (Les ensembles B-mesurables) [D'après Borel, 1898]

Soit E un ensemble de nombres réels inclus dans l'intervalle [0, 1]. Alors s'il est possible d'attacher un nombre m(E) positif ou nul à E ayant les propriétés suivantes, nous dirons que E est B-mesurable :

B1 : Si 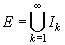      ⊂ [0,1]    avec les intervalles I_k disjoints deux à deux et que 

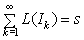
alors m(E) = s.

B2 : Si 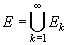    ⊂ [0,1] , avec les E_k disjoints deux à deux et que la mesure de E_k est s_k, alors

  

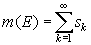
B3 : Si E₁ ⊂ E₂ ⊂ [0,1] et que les mesures de E₁ et de E₂ sont respectivement s₁ et s₂, alors la mesure de l'ensemble E₁- E₂ ={x: x ∈ E₂ et x ∉ E₁} est s₁ - s₂.

Notons que cette définition parut si nouvelle que le mathématicien Schoenflies, qui fut chargé de la recension des travaux en analyse à la fin du 19e siècle, affirma que cette théorie n'avait aucune utilité, car il y avait trop peu d'applications; il préféra les théories calculatoires de Peano et de Jordan [3] .

En utilisant B1, B2 et plus particulière B3, Borel réussit à démontrer plusieurs résultats intéressants touchant la topologie des ensembles. Par exemple, il put construire un ensemble non dénombrable de mesure nulle, démontrer que tout ensemble dénombrable est de mesure nulle et que tout ensemble parfait et limité [4] de l'intervalle [0, 1] est mesurable [5] . Borel recherchait donc à trouver le plus de résultats possibles; il cherchait alors la portée maximale de sa définition. Bien que ce soit un processus de généralisation qui est à l'origine de cette quête, le rôle de ces nouveaux résultats est de justifier le choix des propriétés B1, B2 et B3. En effet, Borel écrit :

[On définit] les éléments nouveaux qu'on introduit, à l'aide de leurs propriétés essentielles, c'est-à-dire de celles qui sont strictement indispensables pour les raisonnements qui doivent suivre [6] .

Ainsi, une propriété est essentielle si elle est utilisée dans les preuves. Dans ce cas, cette propriété change de statuts : elle devient constitutive de la notion.

Ce changement dans le statut des propriétés et le passage du calcul aux propriétés de ce calcul sont des caractéristiques, non pas du processus de généralisation, mais du processus d'abstraction.

4. Une caractérisation logique de la notion de mesure

Nous nous intéresserons maintenant à caractériser logiquement le développement de notions mathématiques et plus particulièrement le passage de la notion de J-mesure à la notion de B-mesure. Pour ce faire, nous utiliserons les caractéristiques logiques du processus d'abstraction réfléchissante introduit par Jean Piaget comme un processus cognitif de développement de l'intelligence d'un individu. Cette version logique de l'abstraction réfléchissante sera ensuite comparée aux recherches d'Aline Robert et de Jean Cavaillès.

4.1  Le processus d'abstraction réfléchissante

Au sujet de l'abstraction réfléchissante, Jean Piaget écrit :

L'abstraction réfléchissante comporte deux moments indissociables : un « réfléchissement » au sens d'une projection sur un palier supérieur de ce qui est emprunté au palier précédent (...) et une « réflexion » au sens d'une reconstruction ou réorganisation cognitives (plus ou moins consciente ou non) de ce qui a été ainsi transféré. [7]

D’abord, le passage de la version calculatoire à la définition par propriétés illustre le passage du palier inférieur au palier supérieur, car la version calculatoire devient un cas particulier de la version par propriétés.  Ensuite, les deux moments dont parlent Piaget s’opèrent comme suit.  D’une part, certaines propriétés ont été « empruntées » à la version calculatoire pour être « réfléchies » au palier supérieur, c’est-à-dire pour devenir constitutive de la nouvelle notion.  Par exemple, la J-mesure de Jordan satisfait les propriétés constitutives de la B-mesure, mais ces propriétés, dans les travaux de Jordan, ne sont pas constitutives de la notion ni ne sont au centre des préoccupations de Jordan.  Il y a alors un changement d’attention de la part de Borel.

D’autre part, la nouvelle notion devient une reconstruction de la notion initiale, c’est-à-dire qu’une nouvelle définition de la notion est proposée dans laquelle certaines propriétés de la notion initiale deviennent constitutives de la nouvelle notion.  Ainsi, nous assistons à un changement dans la compréhension de la notion, car on ne voit plus la notion de la même façon : le changement d’attention a mis en évidence certaines propriétés qui forment maintenant la définition de la nouvelle notion.  De plus, les propriétés constitutives ne sont pas choisies au hasard : elles doivent être utilisées dans les applications de la notion.  Il doit donc y avoir au préalable une recherche de la plus grande extension de la notion initiale et ainsi le processus de généralisation se retrouve dans le processus d’abstraction.  La reconstruction est donc liée au choix des propriétés et implique un changement dans la compréhension de la notion.

Cette reconstruction est aussi accompagnée d'une réorganisation, c'est-à-dire que des notions jusqu'alors considérées comme disjointes sont maintenant intégrées une nouvelle notion. Dans le cas des recherches de Borel, ses applications furent limitées à la théorie des ensembles de points, mais nous verrons que Lebesgue introduira une mesure qui permettra d'intégrer la notion dans le contexte de la théorie de l'intégrale. Ajoutons que, dans certains cas, la réorganisation peut impliquer que des notions perdent leur statut. Nous en donnerons deux exemples dans la prochaine section.

Finalement, le changement d'attention de la part du sujet est nécessaire au processus d'abstraction, mais il n'est pas suffisant, car il faut que les nouvelles propriétés (celles qui sont maintenant visées par le sujet) deviennent constitutives de la nouvelle notion (reconstruction de la notion initiale) et qu'elles permettent d'intégrer de nouvelles connaissances (réorganisation du savoir mathématiques). De plus, nous assistons à un changement dans la compréhension de la notion initiale.

4.2 Les notions didactiques FUGS

Aline Robert propose dans [Robert, 1998] quatre types de notions mathématiques qui sont issues de la combinaison de quatre propriétés ou caractéristiques d'une notion mathématique (le degré de généralisation, le degré de formalisation, le caractère unificateur et la fonction). Un des objectifs de cet article est de présenter des outils didactiques d'analyse de contenus mathématiques qui sont présentement enseignés. Si on veut utiliser les recherches d'Aline Robert pour caractériser le passage des travaux de Jordan aux travaux de Borel, ou plus particulièrement, de la notion de J-mesure à la notion de B-mesure, il faut affirmer que la notion de J-mesure est une notion qui est introduite pour résoudre de nouveaux problèmes précis, en l'occurrence l'interprétation de l'intégrale de Riemann en plusieurs dimensions, alors que la notion de B-mesure est une notion généralisatrice, unificatrice et porteuse d'un nouveau formalisme. Or, ces dernières peuvent se caractériser logiquement par le processus d'abstraction réfléchissante.

D'abord, la notion de B-mesure a un degré de généralisation plus grand que la notion de J-mesure, car il y a superposition d'extensions. En fait, l'extension de la J-mesure sont les ensembles mesurables au sens de Jordan alors que l'extension de la B-mesure sont les opérateurs sur les ensembles qui sont des mesures. Ainsi, la notion J-mesure devient un cas particulier (une instance) de la notion de B-mesure. Or, pour faire une telle superposition d'extensions, il faut reconstruire la notion initiale au sens de l'abstraction réfléchissante, c'est-à-dire qu'il faut identifier des propriétés de la notion initiale qui deviennent constitutives de la nouvelle notion. Donc, cette généralisation est possible grâce à l'abstraction réfléchissante [8] .

Ensuite, l'unification de notions antérieures est aussi une caractéristique du processus d'abstraction réfléchissante. Nous avons appelé cette caractéristique : la réorganisation du savoir mathématique. Par contre, comme nous l'avons mentionné, cette réorganisation, dans les travaux de Borel, fut assez limitée.

Quant au nouveau formalisme introduit par Borel, il est aussi une caractéristique des recherches de Jordan et de Peano. Ainsi, cette caractéristique ne nous permet pas de différencier les notions de J-mesure et de B-mesure.

Nous en concluons que les caractéristiques logiques des notions FUGS sont sensiblement les mêmes que celles du processus d'abstraction réfléchissantes.

4.3 Les recherches philosophiques de Cavaillès

Alain Michel a utilisé les processus du paradigme et de thématisation de Jean Cavaillès [9] dans son livre Constitution de la théorie moderne de l'intégration [10] afin analyser le passage de la version calculatoire de l'intégrale de Lebesgue à la version axiomatique proposée par Lebesgue [11] .
Selon Michel et en utilisant notre terminologie, le paradigme permet de passer d'un cas particulier (une instance qui est donné dans l'immédiat) au cas général (la notion ou une propriété), alors que la thématisation permet d'identifier non pas la notion mais certaines propriétés. Ainsi, le paradigme produit la matière avec laquelle le thématique introduit le nouveau concept en identifiant certaines propriétés dans la matière.

Premièrement, l'introduction de la nouvelle notion ne se fait pas en identifiant ou en isolant n'importe quelle propriété : il faut choisir, comme l'a fait Borel, les propriétés qui permettent de résoudre les problèmes. Comme nous le verrons à la section suivante, certains choix de propriétés ne sont pas bons. Ainsi, le thématique satisfait une des caractéristiques de abstraction réfléchissante.

Deuxièmement, Michel utilise le paradigme comme une abstraction en affirmant que ce processus nous permet de passer d'une instance, comme d'un groupe particulier ou de intégrale de Lebesgue, à la notion de groupe ou aux propriétés de linéarité ou de positivité de l'opérateur intégrale. Or, Cavaillès l'utilise plutôt comme une généralisation [12] , car il affirme que ce processus permet de généraliser successivement la notion d'addition des nombres naturels, aux nombres rationnels puis aux nombres réels. Il y a donc ambiguïté [13] , car le paradigme réfère à deux processus totalement différents : le passage d'une instance à la notion (abstraction) et l'augmentation de l'extension d'une notion (la généralisation).

Troisièmement, le thématique satisfait aussi la caractéristique de la superposition d'extensions. En utilisant le langage philosophique de Cavaillès, « tout sens posant est en même temps sens posé d'un nouvel acte » [14] . Le nouvel acte est la nouvelle notion dont la notion initiale (le sens posant) devient une instance (le sens posé). Michel affirme « les "actes antérieurs" se trouvent (...) "prolongés", mais aussi englobés comme cas particuliers. » [15] . Cette caractéristique, comme nous l'avons mentionné à la section sur les travaux d'Aline Robert, est propre à l'abstraction réfléchissante.

Nous en concluons finalement que le paradigme est une abstraction simple ou une généralisation qui est préalable au thématique. Quant au thématique, il est une abstraction au sens de l'abstraction réfléchissante.

5. Retour sur les travaux de Peano et Jordan

Le fait de choisir des propriétés n'implique pas que la nouvelle notion est une abstraction de la notion initiale. Nous suggérons deux exemples pour illustrer cette thèse.

Peano présenta dans l'introduction du Chapitre 5 Grandeurs géométriques de son livre Les applications géométriques du calcul infinitésimal la notion de collection de magnitudes géométriques principales. Il proposa alors la définition suivante :

Définition (Les magnitudes géométriques principales) [D'après Peano, 1887]

Une collection de magnitudes est dite principale si pour n'importe quel couple M' et M" de magnitudes, alors

1) ou bien M' et M" sont égales, c'est-à-dire que M' et M" peuvent être superposées ou décomposées en parties qui peuvent être superposées,

2) ou bien M' et M" sont inégales, c'est-à-dire que M' et M" peuvent être décomposées en parties telles que chaque partie de M" est égale à une partie de M' et non l'inverse. Dans ce cas, on peut ajouter que M' est plus grande que M".

Les segments linéaires, les polygones et les prismes sont des exemples, suggérés par Peano, de collection de magnitudes principales. Puis, il affirma qu'il existe des collections de magnitudes pour lesquelles aucune des deux caractéristiques n'est satisfaite et que, dans ces cas, il faut « définir avec soin ce que signifie l'égalité entre deux magnitudes et ce que signifie la mesure d'une telle magnitude » [16] . Un des objectifs de ce chapitre est donc de définir la mesure des ensembles d'une collection de magnitudes géométriques non principales ou, plus simplement, de calculer la mesure d'un ensemble quelconque de points de R, de R² et de R³.

Nous avons vu que la P-mesure permet de calculer la mesure d'un ensemble de points de R, de R² et de R³ en utilisant respectivement des segments linéaires, des polygones et des prismes. Il est ainsi possible de généraliser la notion de P-mesure en remplaçant ces objets géométriques par la notion plus générale de magnitudes principales. On utiliserait alors deux suites de magnitudes principales pour calculer, par exemple, l'aire intérieure et l'aire extérieure d'un ensemble du plan.

Or, ce remplacement ne nous sera d'aucune utilité parce qu'il n'est pas possible de démontrer des propositions en utilisant ces deux propriétés [17] . Il y a donc eu identification de propriétés et reconstruction de la notion, mais défaut d'intégration, car les propriétés isolées n'ont pas pu être utilisées pour intégrer de nouvelles connaissances. La nouvelle notion fut donc abandonnée.

Jordan affirma, dans l'introduction de l'article Remarques sur les intégrales définies de 1892, que certaines propriétés des ensembles de points ont été implicitement utilisées dans les démonstrations. Il écrit:

Toutes les démonstrations reposent sur ce double postulatum, que chaque champ [18]  E a une étendue déterminée; et que, si on le décompose en plusieurs parties E₁, E₂, ..., la somme des étendues de ces parties est égale à l'étendue totale. Or ces propositions sont loin d'être évidentes si on laisse à la conception du champ toute sa généralité [19] .

Jordan ne va pas plus loin dans cette tentative de trouver les propriétés essentielles et présenta, comme nous l'avons vu, seulement la version calculatoire de la mesure.

Nous obtenons donc deux notions qui sont définies par une liste de propriétés, mais qui n'ont pas permis d'intégrer de nouvelles connaissances. Elles ne sont donc pas des abstractions des notions calculatoires de mesure. Par contre, on peut noter que, dans ces deux tentatives, le cas fini de la propriété de sigma-additivité (la propriété B2 restreinte au cas fini) fut sélectionné [20] .

6. L'apport de Lebesgue

Nous retrouvons une abstraction et aussi une généralisation de la mesure dans les travaux de Henri Lebesgue (1875-1941) de 1902 et de 1904. Débutons par l'abstraction.

6.1 Le lien entre la théorie de la mesure et la théorie de l'intégrale

Lebesgue proposa une première liste de propriétés dans sa thèse intitulée Intégrale, longueur, aire publiée en 1902 et une seconde, dans son livre Leçons sur l'intégration et la recherche des fonctions primitives de 1904. Il y a un avantage à la seconde, car il lia la théorie de la mesure avec la théorie de l'intégrale. Nous présenterons donc la seconde [21] :

Définition (Les ensembles L-mesurables) [D'après Lebesgue, 1904]

Soit E un ensemble borné de nombres réels. Alors s'il est possible d'attacher un nombre m(E) positif ou nul à E ayant les propriétés suivantes, nous dirons que E est L-mesurable :

L1 : m(E + a) = m(E) pour tout nombre réel a.

L2 : Si {E_n} est une suite dénombrable d'ensembles disjoints deux à deux, alors

     

L3 : m([0, 1]) = 1

Nous retrouvons, dans ce livre de 1904, une version axiomatique de l'intégrale, c'est-à-dire qu'un opérateur sur les fonctions est une intégrale s'il satisfait 6 propriétés ou axiomes. Lebesgue lia la définition de la mesure à la définition de l'intégrale [22] en déduisant les propriétés L1, L2 et L3 des 6 propriétés constitutives de la notion d'intégrale . En fait, pour lier la mesure à l'intégrale, il utilisa la fonction caractéristique d'un ensemble, un concept introduit par De la Vallée-Poussin [23] :

      , 

avec E ⊂[a,b]  et     

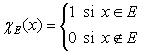
La définition de la L-mesure est une abstraction de la version calculatoire proposée par Lebesgue. Cette version calculatoire s'appelle la mesure extérieure.

6.2 La mesure extérieure

En plus de lier la définition axiomatique [24] de la mesure à celle de l'intégrale, Lebesgue montra aussi que la mesure extérieure, soit sa version calculatoire de la mesure, satisfait les propriétés L1, L2 et L3. Voici la définition proposée en 1902 et en 1904 de la mesure extérieure :

Définition (La mesure extérieure) [D'après Lebesgue, 1902]

Soit E un ensemble borné de nombres réels. Alors la mesure extérieure de E est :

avec {I_k} une suite dénombrable d'intervalles telle que  

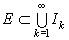
Lebesgue définit la mesure intérieure en utilisant la mesure extérieure et non, comme le fit Jordan, en utilisant une suite d'intervalles inclus dans l'ensemble E. En effet, la mesure intérieure de l'ensemble E ⊂[a,b] se calcule comme suit :

m_i(E) = m([a,b]) - m_e(E^c) , avec E^c le complémentaire de E dans l'intervalle [a, b].

Notons qu'il y a un Lemme caché dans cette démonstration, car Lebesgue supposa que

m(A) = m(A ∩ E) + m(A ∩ E^c).

Ce Lemme fut mis en évidence par Carathéodory et il deviendra une condition pour la mesurabilité au sens de Lebesgue, mais nous y reviendrons.

On obtient que la mesure extérieure de Lebesgue est une généralisation de J-mesure de Jordan, car on peut montrer que

c_i(E) ≤ m_i(E) ≤  m(E) ≤  m_e(E) ≤  c_e(E) 

Donc, si un ensemble est J-mesurable alors il est L-mesurable.

De plus, ces deux notions sont calculatoires et le passage de l'une à l'autre n'a pas nécessité une étude de propriétés ni un changement d'attention de la part du sujet. Ainsi, ce passage n'est pas une abstraction.

7. Le passage à la version contemporaine

Nous proposons de montrer que les notions contemporaines d'espace mesurable et d'espace de mesure ont été développées en utilisant le processus d'abstraction, alors que la notion contemporaine de mesure extérieure a plutôt nécessité le processus de généralisation. Cette étude nous permettra de remarquer qu'une abstraction change la compréhension de la notion, ce qui n'est pas nécessairement le cas pour une généralisation. De plus, ce passage à la version contemporaine mettra en évidence une autre caractéristique du processus d'abstraction, la spécialisation des notions.

7.1 La sigma-additivité

La sigma-additivité est une propriété qui fut sélectionnée à la fois par Borel (B2) et par Lebesgue (L2). Or, cette propriété en implique deux autres qui sont constitutives des notions contemporaines en théorie de la mesure. D'une part, il faut que l'union dénombrable d'ensembles mesurables soit un ensemble mesurable. Cette propriété doit donc être constitutive de la notion d'ensemble mesurable. D'autre part, une autre propriété constitutive de la notion de la mesure est que la mesure de l'union dénombrable d'ensembles mesurables disjoints doit être égale à la somme des mesures des ensembles de l'union. Formellement, nous avons la définition contemporaine suivante :

Définition (Les sigma-algèbres et les espaces mesurables)

Une famille X de sous-ensembles d'un ensemble Ω est une sigma-algèbre si

1) ∅ ∈ X , Ω  ∈ X.

2) Si A ∈ X, alors le complémentaire de A appartient aussi à X.

3) Si (A_n) est une suite d'ensembles de X, alors l'union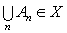      

(Ω, X) est un espace mesurable.

Exemples

Soit Y, un ensemble quelconque. Alors les ensembles suivants sont des sigma-algèbres de Y :

a) {∅, Y}.

b) {∅, E, E^c, Y}, pour un certain ensemble E de Y.

c) L'ensemble des parties de Y est une sigma-algèbre de Y.

d) L'ensemble de Borel B est la plus petite sigma-algèbre qui contient les ouverts de Rⁿ ou plus généralement qui contient les ouverts d'un espace topologique Y.

Nous obtenons donc un ensemble dont on peut mesurer tous ses éléments et, pour les mesurer, on utilisera une fonction qui associera une valeur réelle étendue (R {- ∞, + ∞}) à chacun de ces ensembles mesurables :

Définition (Les espaces de mesure)

Une fonction μ à valeurs réelles étendues définie sur une sigma-algèbre X d'un ensemble Ω  est une mesure si

1) μ(0) = 0.

2) μ(A) ≥ 0, pour tout A ∈ X.

3) Si {A_n } est une suite d'ensembles de X disjoints deux à deux, alors 

       

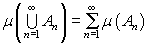
Dans ce cas, (Ω, X, μ) est un espace de mesure.

Exemples :

a) On peut définir une mesure sur l'espace mesurable {∅, E, E^c, Y} comme suit :

μ(∅) = 0, μ(E) = 1, μ(E^c) = 1, μ(Y) = 2

b) On peut aussi définir la mesure extérieure sur l'ensemble B.

On obtient donc que le choix des propriétés constitutives a permis de reconstruire la notion initiale de mesure en deux notions distinctes et ces nouvelles notions peuvent être intégrées à une théorie de l'intégrale. En effet, un espace de mesure peut donc être utilisé pour définir l'intégrale de Lebesgue : Soit (Ω, X, μ), un espace de mesure et soit f : X → R une fonction mesurable. Alors l'intégrale de Lebesgue se définit comme suit : 

      

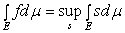
où E ∈ X et s est une fonction simple [25] telle que 0 ≤ s ≤ f.
 

On peut aussi considérer l'ensemble des fonctions mesurables définies sur Y dont l'intégrale de Lebesgue suivante converge :

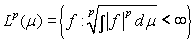
Ajoutons que notre compréhension d'une mesure change, car la propriété de sigma-additivité devient deux notions différentes, alors que notre compréhension de l'intégrale de Lebesgue est conservée, puisqu'elle est toujours définie comme la borne supérieure sur les intégrales de fonctions simples. Par contre, comme les nouvelles notions mettent en évidence certaines propriétés qui étaient implicitement utilisées, on comprend mieux leur utilisation dans la définition d'intégrale et donc ces nouvelles notions abstraites permettent de mieux comprendre l'intégrale de Lebesgue. Le processus d'abstraction implique une meilleure compréhension des notions.

7.2 La mesure extérieure et les ensembles L-mesurables et B-mesurables

Nous allons montrer que la mesure extérieure de Lebesgue peut être généralisée pour devenir une mesure définie sur Rⁿ (ou sur B) dont la mesure des intervalles ou des n-cellules coïncide avec leur volume. En fait, la nouvelle façon de procéder est un ajustement de la technique de Jordan utilisée pour calculer la J-étendue. Rappelons que Jordan se donna un quadrillage dont les côtés des n-cellules avaient la même valeur; ensuite, il le changea pour un nouveau quadrillage plus fin. L'idée de la mesure extérieure est d'utiliser des n-cellules dont les longueurs des côtés sont différentes (Figure 3).

Figure 3 : Le passage de la technique de Jordan à la technique de Lebesgue Le quadrillage proposé par Jordan Le quadrillage proposé par Lebesgue

On retrouve donc que la nouvelle technique ajoute de la flexibilité à la technique de Jordan. La version contemporaine est une généralisation de la mesure extérieure proposée par Lebesgue, car elle conserve la définition proposée par Lebesgue comme un cas particulier.

De plus, la mesure extérieure peut être utilisée pour définir les ensembles L-mesurables. Nous avions mentionné que Lebesgue utilisa un Lemme caché lorsqu'il définit la mesure intérieure. Or, ce Lemme peut être récupéré et utilisé pour définir les ensembles L-mesurables :

Définition (Les ensembles L-mesurables)

Un ensemble E ⊂  Rⁿ  est L-mesurable si

m_e(A)  = m_e(A ∩ E) + m_e(A ∩ E^c) , pour tout ensemble A ⊆ Rⁿ.

La mesure extérieure peut aussi être utilisée sur l'ensemble de Borel  B. On peut ainsi montrer que tous les ensembles B-mesurables sont L-mesurables, mais il existe des ensembles L-mesurables qui ne sont pas B-mesurables (L'argument est basé sur la cardinalité des ensembles). De plus, Vitali présenta en 1905 un ensemble qui n'est pas L-mesurable (il utilisa l'axiome du choix). Ces recherches de la plus grande extension et de contre-exemples sont des activités qui caractérisent le processus de généralisation : on se fixe une façon de définir ou de comprendre une notion et on recherche la plus grande extension de celle-ci.

7.3 La spécialisation

Nous avons mentionné dans la section 7.1 qu'une abstraction permet de mieux comprendre la notion, car la reconstruction met en évidence des propriétés qui étaient implicitement utilisées lors de l'application de la notion. Or, cette mise en évidence peut impliquer une spécialisation des notions mathématiques au sens d'Auguste Comte [26] lorsqu'il parle de la spécialisation du travail : chaque travailleur a une liste de tâches à accomplir différente de celle d'un autre travailleur.

En effet, nous retrouvons plusieurs études différentes ou problèmes à résoudre différents dans les travaux en analyse réelle de la fin du 19^e siècle. Il y avait, par exemple, l'étude de la continuité d'une fonction, le calcul de l'intégrale d'une fonction, l'étude de la convergence d'une suite de fonctions. Or, toutes ces études portaient sur les fonctions réelles à valeurs réelles et utilisaient la métrique « naturelle » de R, en l'occurrence d(x, y) = | y - x |.

Nous avons assisté au cours du 20^e siècle aux développements de nouvelles notions spécialisées, c'est-à-dire de nouvelles notions qui permettaient de résoudre certains (et non pas tous les) problèmes impliquant la notion initiale. Par exemple, on distingue maintenant une métrique, d'une topologie, d'une sigma-algèbre et d'une mesure. On peut ainsi considérer les nombres réels ou, plus précisément, l'espace vectoriel R comme un cas particulier d'un espace métrique, d'un espace topologique ou d'un espace de mesure [27] . Or, chacune de ces nouvelles notions ne permet pas de résoudre tous les problèmes qui peuvent être résolus dans R. Par exemple, on peut définir la continuité d'une fonction dans un espace métrique (ou topologique) et non pas dans un espace de mesure, alors qu'on peut définir la mesure d'un ensemble dans un espace de mesure et non dans un espace topologique. Ainsi, les activités dans l'espace vectoriel R se sont spécialisées et peuvent maintenant être accomplies par des notions ayant des portées d'application distinctes, donc par des notions spécialisées.

De plus, on peut montrer que ces nouvelles notions spécialisées ont été introduites par abstraction. En fait, nous avons vu que l'abstraction permet de reconstruire une notion en mettant en évidence les propriétés essentielles à cette notion. Les propriétés qui caractérisent, par exemple, une métrique sont différentes des propriétés qui caractérisent une topologie et permettent donc de résoudre des problèmes différents. Or, cette différence caractérise la spécialisation des notions et nous en concluons que le processus d'abstraction permet d'introduire des notions spécialisées.

8. L'abstraction versus la généralisation

Nous avons vu que le processus d'abstraction se caractérise par un changement d'attention de la part du sujet et ce changement d'attention permet d'identifier des propriétés constitutives de la nouvelle notion et d'intégrer de nouvelles connaissances.

Le changement d'attention, nécessaire pour faire une abstraction, n'est pas toujours caractérisé par le passage d'un calcul aux propriétés de ce calcul; il peut aussi être caractérisé par l'identification de la propriété qui est implicitement utilisée lorsqu'on applique la notion ou lorsqu'on fait une démonstration. Par exemple, la continuité d'une fonction en un point se définit dans un espace métrique comme suit : soit  f : (X, d_X )→ (Y, d_Y). Alors, 

(∀ε ∈ R^+* )(∃δ ∈ R^+* ) (∀x ∈ X)((d_X (x, x₀) < δ ⇒ d_Y (f((x), f(x₀)) < ε)

Or, lorsqu'on définit la continuité en un point dans un espace topologique, on se rend compte qu'il n'est pas nécessaire de connaître la distance entre x et son voisinage. On attire alors notre attention sur le traitement des ouverts par l'image inverse de la fonction. On obtient ainsi la définition suivante : soit f : (X, Γ_X)→ (Y, Γ_Y). Alors, 

(∀ V ⊆ Γ_Y)( f(x₀) = y₀ ∈ V ⇒ (∃ U ⊆ Γ_X)  f ^-1(V)⊆ U ).

On comprend donc mieux la notion de continuité, car on a identifié la propriété constitutive de la notion, en l'occurrence une propriété implicitement utilisée lorsqu'on applique la notion.

De plus, le processus d'abstraction s'attaque à la nature de la notion, car on tente de répondre aux questions suivantes : quelles sont les propriétés de la notion qui sont nécessaires pour résoudre « plus efficacement » le problème; quelles sont les propriétés de la notion qui sont « vraiment » utilisées lorsqu'on applique la notion.

Par contre, une des caractéristiques du processus de généralisation est la recherche de la plus grande extension d'une notion donnée. Par exemple, le passage de la notion d'étendue de Jordan à la notion de mesure extérieure de Lebesgue est une généralisation, car la seconde notion permet de calculer plus d'ensembles mesurables, tout en conservant la première comme un cas particulier. On s'intéresse alors à des questions portant sur l'extension de la notion : Est-ce que les ensembles B-mesurables sont inclus dans les ensembles L-mesurables? Est-ce que les propriétés B1 à B3 peuvent être déduites des propriétés L1 à L3? Existe-t-il des ensembles non-L-mesurables [28] ?

Cet exemple illustre aussi le cas d'une généralisation qui n'est pas une abstraction. Ainsi une abstraction implique une généralisation, mais il existe des généralisations qui ne sont pas des abstractions.

Finalement, d'un point de vue didactique, l'abstraction est un processus plus difficile, car il nécessite un changement d'attention de la part de l'élève : il faut que l'élève voit les notions autrement. De plus, il faut que l'élève passe des objets aux actions sur ces objets. Par exemple, les élèves ont de la difficulté à concevoir que les fonctions (ou les matrices) peuvent devenir des éléments d'un ensemble plus général, comme des « vecteurs » d'un espace vectoriel.

9. Bibliographie

Bartle, Robert G., 1966, The Elements of Integration and Lebesgue Measure, New York : John Wiley and Sons, 1995.

Beth, Evert W., Piaget, Jean, 1961, Épistémologie mathématique et psychologie : Essai sur les relations entre la logique formelle et la pensée réelle, Paris : PUF.

Borel, Émile, 1898, Leçons sur la théorie des fonctions : principes de la théorie des ensembles en vue des applications à la théorie des fonctions, 4 éd., Paris : Gauthier-Villars, 1950.

Cavaillès, Jean, 1997, Sur la logique et la théorie de la science, Paris : Vrin.

Comte, Auguste, 1830-1842, Cours de philosophie positive, Paris : Hatier septembre, 1982.

Dugac, Pierre, 2003, Histoire de l'analyse : autour de la notion de limite et de ses voisinages, Paris : Vuibert.

Hawkins, Thomas, 1975, Lebesgue's Theory of Integration : its Origin and Development, New York : Chelsea Publishing company.

Hawkins, Thomas, 1980, « The Origins of Modern Theories of Integration, » in From the Calculus to Set Theory 1630-1910, éd Grattan-Guinness, London : Duckworth. p. 149-219.

Henriques, Gil, Piaget, Jean, 1978, Recherche sur la généralisation, Paris : PUF.

Hochkirchen, Thomas, 2003, « Theory of Measure and Integration form Riemann to Lebesgue, » in A History of Analysis, éd. Hans Niels Jahnke, Providence, RI : American Mathematical Society, p. 261-290.

Lebesgue, Henri, 1901, « Sur une généralisation de l'intégrale définie », Comptes rendus hebdomadaires des séances de l'Académie des sciences, 132, p. 1025-1028. [Sur CultureMATH - Pdf, 75.3 ko]

Lebesgue, Henri, 1904, Leçons sur l'intégration et la recherche des fonctions primitives, 2e éd, Paris : Gauthier-Villars, 1928. [Sur CultureMATH - Pdf, 4.63 Mo]

Michel, Alain, 1992, Constitution de la théorie moderne de l'intégration, Paris : Vrin.

Peano, Giuseppe, 1883, « On the Integrability of Functions », in Kennedy, Hubert C., 1973, Selected Works of Giuseppe Peano, Toronto°: University of Toronto Press, p. 37-43.

Peano, Giuseppe, 1887, « Geometrical Magnitudes », in Kennedy, Hubert C., 1973, Selected Works of Giuseppe Peano, Toronto°: University of Toronto Press, p. 67-74.

Piaget, Jean, 1975, L'équilibration des structures cognitives : Problème central du développement, Paris : PUF.

Pier, Jean-Paul, 1996, Histoire de l'intégration : vingt-cinq siècles de mathématiques, Paris°: Masson.

Robert, Aline, 1998, « Outils d'analyse des contenus mathématiques à enseigner au lycée et à l'université », Recherches en Didactique des Mathématiques, Vol. 8, no. 2, p. 139-190

Rudin, Walter, 1966, Real and Complex Analysis, 3^e éd, New York : McGraw-Hill, 1987.

^{Villeneuve, Jean-Philippe, 2008, Types de généralisations et épistémologie des mathématiques : de l'intégrale de Cauchy à l'intégrale de Lebesgue, Thèse, Université de Montréal.}

^{Villeneuve, Jean-Philippe, 2009, « Les généralisations de la notion mathématique d'intégrale au 19e siècle », CultureMATH, [en ligne - 15 janvier 2009).} 

^{Villeneuve, Jean-Philippe, 2010, "Les types de généralisations en mathématiques", Bulletin de l'AMQ, en révision.}