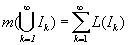
Il y avait une autre version calculatoire de la mesure dans les travaux de Stolz, de Cantor et de Harnack sur l'étendue extérieure d'un ensemble, mais elle ne nous sera pas utile pour notre analyse.
Il y a un Lemme caché dans les travaux de Jordan : Jordan supposa qu'un ensemble majoré de nombres réels admet une borne supérieure. Il fit donc la même erreur que Weierstrass lorsqu'il démontra le Théorème des valeurs intermédiaires (Consulter [Dugac, 2003, p. 126]).
Consulter au besoin [Hawkins, 1975].
Un ensemble est parfait, selon Borel, s'il est identique à son dérivé, donc à l'ensemble de ses points limites. Un ensemble est limité, selon Borel, si la distance entre deux éléments de l'ensemble est inférieure à un certain nombre.
Dans ce dernier cas, Borel supposa que le complémentaire de l'ensemble parfait et limité était composé d'un ensemble dénombrable d'intervalles, voir [Borel, 1898, p. 50].
[Borel, 1898, p. 48n]
[Piaget, 1975, p. 41]
Il faut ajouter qu'il y a d'autres sortes de relations de cas particulier entre deux notions : le choix de paramètres (un vecteur de R² versus un vecteur de Rn), le changement de contextes (la continuité d'une fonction dans R versus la continuité dans un espace métrique), l'ajout de propriétés (la notion de monoïde versus la notion de groupe). Ces types de relation engendrent des généralisations qui ne sont pas des abstractions. [Villeneuve, 2010]
Il faut quand même mentionner que les recherches de Cavaillès ont eu lieu avant les travaux de Thomas Kuhn en philosophie des sciences dans lesquels le concept de paradigme est important, voire central, et qu'il prend plusieurs sens.
[Michel, 1992]
Lebesgue en 1902, puis en 1904 a proposé deux nouvelles façons de définir l'intégrale, l'une calculatoire, l'autre axiomatique (Pour les détails sur ces façons de définir l'intégrale, on peut aussi consulter [Villeneuve, 2009]).
[Cavaillès, 1997, p. 46]
Et cette ambiguïté semble générer une contradiction entre les travaux de ces deux philosophes : lorsque l'un parle d'un développement transversale de connaissances, l'autre parle d'un développement longitudinal. Or, le processus d'abstraction permet le transversal, alors que la généralisation, le longitudinal et donc lorsqu'on associe correctement le paradigme au bon processus, la contradiction est levée.
[Cavaillès, 1997, p. 46]
[Michel, 1992, p. 87]
[Peano, 1887, p. 67] La traduction est mienne.
On peut essayer de démontrer le théorème de Jordan en utilisant ces deux caractéristiques, mais on n'y arrivera pas.
Un champ est un ensemble de points de Rn.
[Jordan, 1892, p. 69-70]
Dans la citation de Jordan, il n'est pas clair que la notation E1, E2, ..., réfère à une liste infinie d'ensembles, car Jordan utilise aussi cette notation pour parler de n variables indépendantes (voir page 71 de [Jordan, 1892]). Ainsi, nous pouvons seulement affirmer que le cas fini de la propriété de sigma-additivité fut sélectionné.
Dans la version de 1902, la propriété L3 était m(E) ≠ 0, pour un certain ensemble E. Or, il faut ajouter la nouvelle propriété L3, si l'on veut que la propriété suivante soit vraie : soit {Ik} une suite d'intervalles disjoints deux à deux. Alors
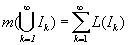
On utilise le théorème de la convergence dominée de Lebesgue (qui est en fait l'axiome 6) pour démontrer la propriété L2.
Voir [Lebesgue, 1928, p. 38].
On utilise le théorème de la convergence dominée de Lebesgue (qui est en fait l'axiome 6) pour démontrer la propriété L2.
Une fonction est dite simple si elle prend un nombre fini de valeurs. Par exemple, soit E1, ..., En, n ensembles disjoints et soit a1, ..., an, n nombres réels. Alors
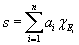
est une fonction simple.
Consulter [Comte, 1830-1842, 1re Leçon, II]
L'opérateur « en tant que », introduit par Aristote et qui caractérise l'abstraction aristotélicienne, permet d'isoler une propriété d'une notion. Par exemple, on peut écrire : R en tant qu'un espace métrique (R, d(x, y)), ou R en tant qu'un espace topologique (R, U(x, r) = {y : | x - y | < r}). Cet opérateur permet donc d'identifier la propriété de l'objet qui nous intéresse ou qui est utilisée.
Pour plus d'information sur les processus de généralisation, consulter [Villeneuve, 2009] sur CultureMATH.