Encart 1 : Le transfert des apprentissages

Nous affirmons que la technique utilisée notamment par Cauchy pour généraliser l’intégrale de Cauchy pour les fonctions continues (IC1) aux intégrales impropres (I*C1 ou IC2) s’apparente à une technique qui permet d’effectuer un transfert d’un apprentissage.  En effet, Jacques Tardif propose la définition minimale suivante d’un transfert d’un apprentissage :
 

Dans une situation de transfert d’un apprentissage, une personne recontextualise dans une tâche cible une connaissance construite ou une compétence développée dans une tâche source.[1]

Un transfert se produit donc entre une tâche source et une tâche cible.  On peut interpréter une tâche comme un problème à résoudre et ainsi un transfert a lieu lorsque la personne est en mesure de résoudre le nouveau problème en « recontextualisant » dans ce nouveau problème une connaissance construite ou une compétence développée utilisée dans la résolution du problème initial.  Dans ce cas, une technique de transfert permet de faire une telle recontextualisation.
 
Pour notre part, nous affirmons que Cauchy a utilisé une technique de transfert pour recontextualiser l’intégrale de Cauchy (IC1) dans le contexte des fonctions continues par morceaux et a ainsi développé la notion d’intégrale de Cauchy pour les fonctions continues par morceaux (IC2).  En effet, dans ce cas, la tâche source est de calculer l’intégrale d’une fonction continue et la tâche cible est de calculer l’intégrale d’une fonction continue par morceaux.  La façon de résoudre le problème de la tâche source est de calculer les sommes de Cauchy (ou d’appliquer le Théorème fondamental du calcul, car Cauchy a démontré ce théorème dans le contexte des fonctions continues). 
 Or, il est possible d’utiliser IC1 pour accomplir la tâche cible.  En effet, soit par exemple la fonction   qui est une fonction continue par morceaux sur l’intervalle [-1, 2].  Ainsi, pour intégrer cette fonction, la technique à utiliser pour rendre cette fonction continue est la suivante : on choisit un petit nombre positif ε.  On obtient alors que la fonction est continue sur les deux intervalles [-1, -ε] et [ε , 2] et donc qu’on peut utiliser (IC1). On passe ensuite à la limite.  Dans le détail, nous avons :

        
                                  

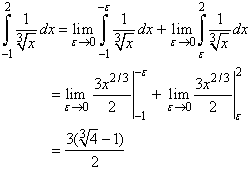
Donc, pour cet exemple, la technique de transfert est de tronquer l’intervalle d’intégration pour obtenir une fonction continue.  Ensuite, on passe à la limite et, si elle existe, alors la fonction est intégrable.

Notons que nous aurions pu aussi utiliser une terminologie de Piaget et affirmer que la technique de transfert est une technique d’accommodation d’une notion assimilée.  

Mentionnons au passage qu’il y a deux sortes de transferts.  Nous pouvons montrer que le transfert vertical permet d’ajouter de la complexité à la connaissance transférée, alors que le transfert horizontal, de changer la connaissance de contextes.  Nous utiliserons donc cette distinction pour introduire deux sortes de généralisations conservatives.

 

Retour au Sommaire

Retour à l'article : Section 3.1



[1] Tardif, Jacques, 1999, Le transfert des apprentissages, Montréal : Les éditions logiques, p. 86