
Le problème de Pappus
Version [pdf ] (1.8 Mo, 24 p.).
L'intérêt pour le problème de Pappus parcourt toute la carrière scientifique de Newton. [1] Bien qu'il ait donné des contributions considérables aussi au cas général, [2] c'est surtout au cas de quatre lignes qu'il a réservé la plus grande attention.
Rappelons la formulation de ce problème dans le cas de quatre lignes. [3]
|
Figure 1
 Le problème de Pappus |
Les droites EF, AD, AB, GH sont données avec quatre angles qui sont donnés en même temps.Il s'agit de déterminer le lieu des points C tels que, en conduisant les lignes CF, CD, CB, CH, sur EF, AD, AB, GH suivant les angles donnés, la raison de CB × CD à CF × CH soit donnée. On voit immédiatement que les points d'intersection E, G et les points d'intersection de AD, EF, et de AD, GH qui ne sont pas indiqués dans la figure de la Géométrie de Descartes que j'ai reproduite) sont des points du lieu.
La solution (analytique) du problème de Pappus est une sorte de « fil rouge » qui relie les trois livres de La Géométrie de Descartes et dont Descartes était à juste titre très fier. Newton, après ses années d'apprentissage toutes «cartésiennes», devient de plus en plus critique envers l'utilisation exclusive des outils algébriques pour résoudre les problèmes géométriques. Dans le cas de quatre lignes il oppose à la solution cartésienne [4] une pluralité de solutions qui poursuivent l'idéal de retrouver la solution «parfaite» possédée, à son avis, par les Anciens.
Le problème de Pappus dans le cas de quatre lignes est considéré par Newton comme équivalent à la détermination d'une conique passant par cinq points. Puisqu'il suppose toujours (implicitement) que l'on doit chercher la solution dans une région donnée du plan, il ne pose jamais la question de l'existence de deux solutions, question qui était l'objet d'un âpre polémique entre Descartes et ses adversaires. [5]
La première solution du problème de Pappus à quatre lignes, opposée a celle de Descartes, est donnée par Newton au moyen de sa célèbre construction organique des coniques, envoyée à Collins (sans démonstration) dans la lettre du 20 août 1672. [6] Cette solution est reprise plusieurs fois. Dans la Solutio Problematis Veterum de Loco Solido [7] elle est donnée après la solution newtonienne du problème de Pappus. La démonstration aussi dépend de la solution donnée à ce problème.
La construction organique est donnée de façon semblable dans le De Motu. [8]Enfin dans les Principia [9] on a la formulation classique. Dans la Section 3 nous donnerons la description de cette construction et expliquerons son usage pour construire une conique par cinq points. La démonstration de Newton sera exposée dans la Section 6.
Toutefois dans les années qui suivent la solution du problème de Pappus par la construction organique, Newton s'est arrêté de façon détaillée sur le cas particulier du problème de Pappus où la solution est donnée par un cercle. C'est l'exemple choisi par Descartes dans La Géométrie. [10] Probablement Newton projetait de considérer ce cas particulier à l'intérieur d'un traité de géométrie élémentaire, mais ce traité, comme la plus ambitieuse Geometria de sa vieillesse n'a jamais vu le jour. [11] Dans la Section 4 nous proposons une démonstration possible du résultat indiqué par Newton.
Dans la Veterum Loca solida Restituta [12] une construction intéressante d'une conique par cinq points est donnée, accompagnée d'une piquante critique envers Descartes. Après avoir observé que Descartes a eu tort de prétendre avoir donné une solution inconnue par les Anciens [13] il observe :
Des critiques semblables envers Descartes accompagnent tous les textes où Newton s'occupe du problème de Pappus. Nous ne rendrons pas compte de ces critiques bien qu'elles soient du plus grand intérêt surtout lorsqu'elles se prolongent par des considérations méthodologiques. [15] Les résultats contenus dans la Veterum Loca solida Restituta sont exposés dans la Section 5.
La Solutio Problematis Veterum de Loco Solido est un texte plutôt élaboré, qui, après la révision dans le De Motu, constitue la base de la Cinquième Section du Premier Livre des Principia. [16]
Dans la Section 6 nous donnerons un exposé détaillé de la partie la plus importante de ce texte et dans la Sous-section 6.3 nous ferons une comparaison avec les Principia.
La composition de la Arithmetica Universalis [17] se place chronologiquement entre la Solutio Problematis Veterum de Loco Solido et le De Motu. Du point de vue de la « Geometria Veterum » on n'a pas de grandes choses. Mais il y a une solution vraiment «cartésienne» du problème de Pappus. Nous exposerons cette solution dans la Section 7.
Dans
les deux dernières Sections nous effleurerons les
idées de Newton qui, à partir du
problème de Pappus acquièrent une importance
méthodologique considérable.[18]
Newton a toujours considéré les propositions III.17-III.19 des Coniques d'Apollonius et les propositions VIII.13, VIII.14 des Collections de Pappus comme une connaissance de base avec laquelle son lecteur devait être familier.
Nous nous limitons ici à présenter le contenu de la III.17 des Coniques. [19]
|
Figure 2
 La proposition II.17 d'Apollonius |
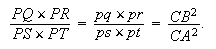 [20]
[20]Newton n'a jamais repris les démonstrations d'Apollonius. Au contraire les propositions de Pappus ont étés élaborées de nouveau plusieurs fois.
Comme nous l'avons déjà écrit dans la Section 1, cette construction est exposée dans une lettre à Collins de 1672. [21] On peut la décrire facilement à l'aide de la Figure 3 suivante.
|
Figure 3
 La construction organique des coniques 1 |
Cette construction nous donne immédiatement la possibilité de tracer une conique de laquelle cinq points sont donnés (voir la Figure 4 suivante). Supposons qu'une conique soit donnée par les points A, B, C, P, Q et considérons les trois points A, B, C. Ces points déterminent les angles BAC, ABC qui peuvent être utilisés comme angles tournants autour des sommets A, B. Si l'on tourne ces angles de façon que deux des leurs côtés se coupent au point P, les autres côtés par leur intersection donneront le point P'. En utilisant le point Q on obtient le point Q' et donc la ligne P'Q'. Il est facile de voir (puisque une conique est déterminée par cinq points) que à partir de cette ligne par le moyen de la construction organique avec les angles BAC, ABC et les pôles B, C on trace la conique par les cinq points donnés. [22]
|
Figure 4
 La conique par cinq points |
Dans (MP, vol.4, p. 230-269) Whiteside a rassemblé plusieurs problèmes de géométrie élémentaire, dont beaucoup fournissent des propriétés du cercle. Ceux qui sont indexés par les nombres 12, 14, 15 correspondent à des cas particuliers du problème d Pappus. Voyons le numéro 15, que Newton énonce sans démonstration, mais pour lequel la démonstration est suggérée par le choix même des données.
|
Figure 5
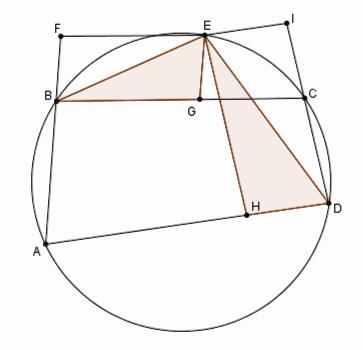 Le problème de Pappus dans le cas du cercle |
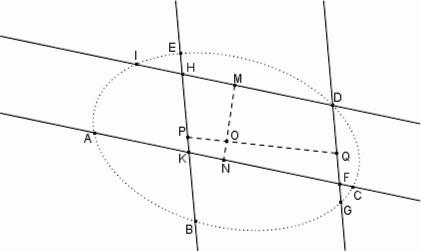
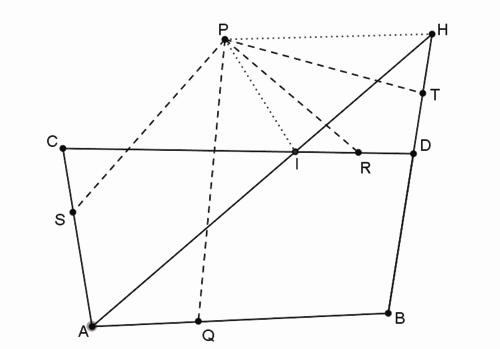
Si dans un cercle quelconque ABCD le trapèze ABCD est inscrit, et à partir d'un point arbitraire E de la circonférence l'on mène les lignes EF, EG qui forment avec les côtés AB, BC le parallélogramme EFBG et les lignes EH, EI qui forment avec les côtés AD, DC le parallélogramme EHDI, le rectangle GE x EH contenu par les lignes menées sur les côtes opposés est égal au rectangle EF× EI contenu par le lignes menées sur les côtés restants.
Toute la démonstration consiste simplement à prouver que les triangles EBG et DEH sont semblables. Évidemment ABC = BFE = BGE. L'angle CDH est supplémentaire de DHE et, puisque ABCD est inscrit dans un cercle, l'angle CDH est aussi supplémentaire de ABC. Il s'ensuit que DHE = BGE.
L'angle CBE est égal à CDE et puisque EH // DI , l'on a CDE = DEH. La similitude des triangles EBG, DEH est prouvée. Il s'ensuit que BG : EG = EH : HD. Mais BG = EF, HD = EI et donc EF × EI = EG × EH.
Si
l'on substitue à EF, EG, EH, EI
les perpendiculaires EF', EG', EH', EI', on a
évidemment ![]() et
et ![]() et la même chose arrive si l'on prend les angles comme Newton
le déclare. On est ramené au cas
précédent. [24]
et la même chose arrive si l'on prend les angles comme Newton
le déclare. On est ramené au cas
précédent. [24]
Remarque: Newton ne donne pas la Proposition réciproque, qui toutefois est presque évidente. Si ABCD est un trapèze qui peut être inscrit dans un cercle, et (avec la même structuration des données) EF × EI = EG × EH, le point est sur le cercle par A, B, C, D.
En fait, l'égalité DHE = BGE est donnée par la simple considération du parallélisme, et ne dépend pas de l'hypothèse que E soit sur le cercle passant par A, B, C, D . De EF × EI = EG × EH il s'ensuit que EF ( = BG) : EG = EI ( = HD) : EH et donc les triangles EBG et DEH sont semblables. Donc EBC = HED = EDC. Les angles égaux EBC, EDC sous-tendent le même segment EC et donc les points E, B, C, D sont sur un même cercle, qui ne peut être que le cercle passant par A, B, C, D.
Ce bref texte est composé de deux propositions seulement, que constituent la solution de deux problèmes. [25]
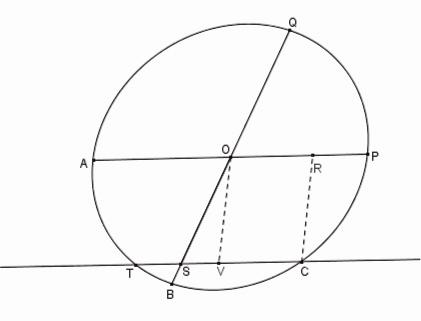
Décrire une conique qui contient les trois points A, B, C et a son centre en O.
Supposons donc qu'une conique soit donnée par les trois points A, B, C et son centre O .
|
Figure 6
 |
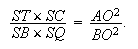
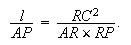
e 2 : Construire une conique qui contient le cinq points A, B, C, D, E.
|
Figure 7
 |
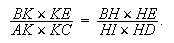

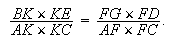
Pour la solution de problème de Pappus il s'agit seulement de déterminer cinq points :
Après ces prémisses, il ne reste qu'à rechercher cinq points par lesquels la figure passe pour mener à bien la composition du lieu solide. [28]
Puisque quatre points sont donnés immédiatement [29]
il s'agit simplement d'utiliser la condition de Pappus pour trouver un
cinquième point. Puisque la solution de Newton est reprise
dans la Solutio
problematis Veterum de
loco solido sans changements essentiels, nous la donnerons
dans la Section suivante.
Le texte de ce manuscrit commence par le théorème suivant. [30]
Si l'on mène d'un point P d'une conique aux quatre côtés étendus à l'infini AB, CD, AC, BD d'un quadrilatère inscrit dans cette conique un nombre égal de lignes droites PQ, PR, PS, PT qui forment chacune un angle donné avec chacun des quatre côtés du quadrilatère, le produit PQ × PR de deux lignes menées sur deux côtés opposés sera en raison donné au rectangle PS × PT des droites tirées aux deux autres côtés opposés. [31]
La démonstration est conduite en considérant trois cas, dans un style qui évoque la stratégie utilisée (selon notre reconstruction) pour le problème du cercle (on peut voir la Section 4).
|
Figure 8
 |
La droite qui passe par les milieux de A, C et B, D est un diamètre. Soit O le point d'intersection de ce diamètre avec PQ . PO sera une ordonnée à ce diamètre, puisque sa direction est celle conjuguée. Si l'on prend OK = PO dans la direction opposée on a un autre point K de la conique.
De la
III.17 d'Apollonius il s'ensuit que le rapport 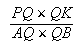 est donné. Mais OQ = OR, QK = PR et par
conséquent, puisque
est donné. Mais OQ = OR, QK = PR et par
conséquent, puisque
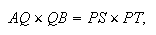
il s'ensuit que
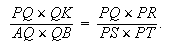 Le
rapport
Le
rapport ![]() est donc donné.
est donc donné.
Voyons le second cas. Les côtés AC et BD ne sont plus parallèles, mais PR, PQ sont encore pris parallèles à AC, pendant que PS, PT sont pris parallèles à AB.
|
Figure 9
 Proposition 1 : Le second cas |
Le
triangle BTt est semblable au triangle DBN.
Il s'ensuit que Bt :
Tt = DN : BN. Mais Bt = PQ,
et donc PQ : Tt = DN : BN.
Puisque Rr : DM = CR : CD = AQ : AN et AQ = PS,
on a Rr : DM = PS : AN et Rr : PS = DM : AN.
En composant les rapports, on a
(6)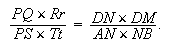
Si l'on considère le quadrilatère ADNC, on peut utiliser ce que nous avons démontré dans le premier cas :
(7)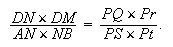
Puisque D est donné, la valeur du rapport au second membre ne dépend pas de la position de P. La comparaison de (6) et (7) donne
(8)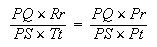
et donc Pr : Pt = Pt : Tt et (Pr - Rr) : Pr = (Pt - Tt) : Pt.
Puisque Pr - Rr = Pr et Pt - Tt = PT on a PR : Pr = PT : Pt, c'est à dire
(9)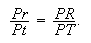
Dans
le deuxième membre de (7)
on peut substituer au rapport ![]() le rapport
le rapport ![]() et donc le
rapport
et donc le
rapport
(10)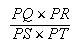 est donné.
est donné.
Voyons le troisième cas.
|
Figure 10
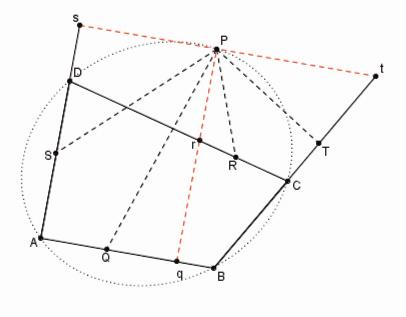 Proposition 1 : Le
troisième cas
|
 sont aussi donnés et donc le rapport
sont aussi donnés et donc le rapport  est donné.
est donné.
Remarque : Dans une
étape
intermédiaire de la démonstration du
deuxième cas du Théorème 1, Newton a prouvé que ![]() .
Si nous imaginons que la conique soit donnée par les points
A, B, C, P, d cette
égalité donne une caractérisation des
autres points D de la conique. On a un cas particulier (puisque AC //
Bd ) de la
génération homographique. Le cas plus
général est l'objet de la Proposition
cinquième, que nous proposons avant la Proposition
destinée à la détermination d'un
cinquième point à partir de la condition de
Pappus. [32]
.
Si nous imaginons que la conique soit donnée par les points
A, B, C, P, d cette
égalité donne une caractérisation des
autres points D de la conique. On a un cas particulier (puisque AC //
Bd ) de la
génération homographique. Le cas plus
général est l'objet de la Proposition
cinquième, que nous proposons avant la Proposition
destinée à la détermination d'un
cinquième point à partir de la condition de
Pappus. [32]
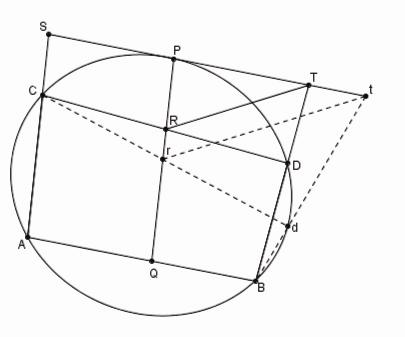
Si entre les points donnés A, P d'une conique arbitraire, un parallélogramme AQPS est inscrit, [33] et si deux côtés AQ, AS sont prolongés jusqu'à couper la courbe en B et C, et qu'ensuite par les points B et C on mène les lignes BD, CD vers un cinquième point arbitraire D de la conique, et que ces lignes coupent les côtés opposés PS et PQ en T et R, la raison de PR à PT sera donnée. Et réciproquement si la raison de PR à PT est donnée, le point D sera sur une conique qui passe par les points A, B, P et C. [34]
Nous nous limiterons à proposer la démonstration de la partie directe de l'énoncé. La partie réciproque s'obtient facilement en renversant les égalités.
|
Figure 11
 Proposition 5
|
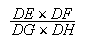
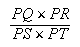
Avant de voir l'utilisation de cette Proposition pour tracer une conique, voyons comment la condition de Pappus peut être exploitée pour avoir cinq points d'une section conique.
Déterminer un point P tel que, si l'on conduit les quatre lignes PQ, PR, PS, PT sur quatre autres lignes données de position AB, CD, AC, BD selon des angles donnés, le rectangle PQ × PR soit en raison donnée au rectangle PS × PT. [35]
|
Figure 12
 Un point de la section conique |
Puisque les rapports ![]() et
et ![]() sont
donnés à leur tour,
sont
donnés à leur tour, ![]() est
donné [36]
et enfin le point P
est donné.
est
donné [36]
et enfin le point P
est donné.
Tous ces résultats nous donnent une façon simple de déterminer une conique par cinq points.
Définir une section conique qui passe par cinq points. [37]
Considérons la Figure 13, qui correspond aux données du Théorème 2.
|
Figure 13
 La génération homographique d'une conique |
.
Ce théorème a un rôle stratégique très important. On peut le voir à l'œuvre dans les Théorèmes 5 et 6, pour démontrer la construction organique et pour une généralisation intéressante de la génération homographique.
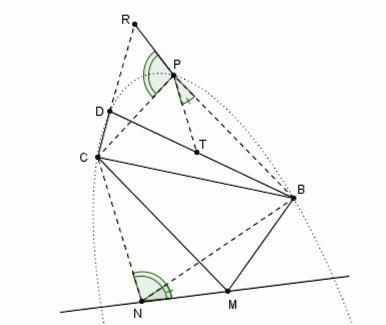
Si deux lignes BM, CM conduites par les points donnés B, C se coupent en un point M d'une ligne MN donnée de position et si deux autres lignes BD, CD sont menées, formant des angles donnés MBD, MCD avec les deux lignes précédentes menées par les points B, C ; je dis que les deux dernières lignes tracent, par leur intersection D un lieu solide. Réciproquement, si les lignes BD, CD tracent un lieu solide qui passe par les points B, C, G et quand ces lignes se coupent en le point G du lieu les autres deux coïncident avec la ligne BC, le point M appartiendra à une ligne donnée de position. [39]
|
Figure 14
 La démonstration de la construction organique 1 |
Par hypothèse on a donc MBD = NBP et MCD = NCP. Si l'on soustrait les parties communes, on a NBM = PBT et NCM = PCR. Il s'ensuit que le triangle NBM est semblable à PBT et le triangle NCM est semblable à PCR . On a donc
PT : NM = PB : NB et PR : NB = PC : NC.
Mais
PB et NB sont donnés, ainsi que PC
et NC.
Il s'ensuit que le rapport ![]() et
donné. En conséquence du
Théorème 2
le point D décrit une conique.
et
donné. En conséquence du
Théorème 2
le point D décrit une conique.
Pour la partie réciproque nous utiliserons une nouvelle figure. [41]
|
Figure 15
 La démonstration de la construction organique 2 |
Donc, en prenant deux autres points G', G'', avec les mêmes angles, par les intersections des autres côtes [43] on détermine les points M, N, et donc une droite MN. On démontre facilement que, si D est un point arbitraire de la conique projeté par les côtés CD, BD des angles donnés tournants, les autres côtés se coupent en un point D' sur la ligne MN (voir la Figure 16). [44]
|
Figure 16
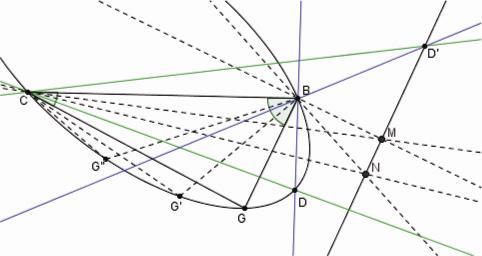 La démonstration de la construction organique 3 |
L'incohérence des contenus de la Section 5 dans les Principia a été observé plusieurs fois. Newton lui même avait projeté d'en disposer les résultats dans un traité spécifique sur la géométrie des Anciens en le séparant des questions dynamiques et physiques. [45]
Nous ne voulons pas donner ici une analyse détaillée des différences entre la Solutio problemati Veterum de Loco Solido et le texte de la Section 5 des Principia, [46] mais simplement proposer quelques observations fonctionnelles à notre exposé.
En premier lieu, il faut souligner que Newton a cherché à atténuer le caractère de la Solutio, clairement consacrée à opposer à la solution cartésienne du problème de Pappus à quatre lignes la vraie (à son avis) solution des Anciens. [47] Le titre de la Section devient Inventio Orbium ubi umbilicus neuter datus et, dans la mesure du possible, loci solidi et conicæ deviennent trajectoires. [48]
Certains résultats qui ont un caractère plus explicitement projectif ne trouvent plus place dans le texte des Principia. En fait ils sont très intéressants en eux mêmes, mais leur importance pour les trajectoires des planêtes ne semble pas évidente, même à Newton.
Un bon exemple est donné par la Proposition 12.
Si deux lignes CD, BD en tournant autour des points donnés C, B coupent deux autres lignes données de position HI, HK et les longueurs de ces lignes données de positions sont réciproquement déterminables par simplicem geometriam : [49] le lieu d'intersection de deux lignes mobiles D sera une conique qui passe par les points C, B autour desquels elles tournent. [50]
|
Figure 17
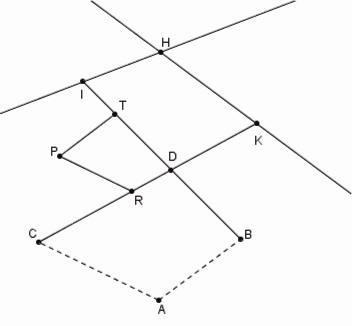 La Proposition 12 |
La démonstration de ce théorème a un caractère projectif bien plus évident que les démonstrations des théorèmes précédents. En fait, ces considérations sur les limites sont spécifiques de la géométrie projective naissante et n'ont rien à faire avec la géométrie des Anciens, bona pace de Newton.
Dans l'Arithmetica Universalis, après la solution du problème de déterminer une conique par cinq points, une solution semblable à celles que nous avons vues, Newton propose une solution «per Algebram solam». [54] Aux yeux d'un lecteur moderne la chose peut paraître banale. Mais en fait il s'agit d'une des premières caractérisations d'une courbe algébrique, à partir de la forme de son équation, en imposant le passage par un certain nombre de points donnés.
|
Figure 18
 Une Conique par cinq points "per
Agebram"
|
Dans les dernières années de la carrière scientifique de Newton, le problème de Pappus acquiert un rôle différent : il n'est plus un objet à traiter individuellement, en opposant (plus ou moins explicitement) sa solution à celle de Descartes. Il vient à être considéré à l'intérieur d'un discours méthodologique plus large où le vrai objectif est celui de construire une mathématique qui hérite de l'esprit de la mathématique classique. L'analyse doit être seulement une étape préliminaire à garder pour soi par le mathématicien. La synthèse finale doit seule être exposée. [56] En outre, non seulement le style de la mathématique ancienne doit être préservé, mais, dans la mesure du possible, les outils eux même de cette discipline doivent êtré employés.
Un bon exemple est donné par la solution du problème de Pappus dans l'Analysis geometrica, un manuscrit de 1691 reproduit dans (MP, vol. 7, p. 200-221).
La solution est toujours réduite à la détermination d'un cinquième point en plus des quatre donnés naturellement par le problème, mais cette fois c'est la De sectione determinata qui entre en scène, probablement par le moyen des notices sur ce texte données par Pappus. [57]
|
Figure 19
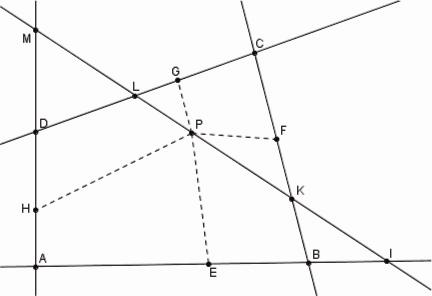 Newton et la De Sectione Determinata |
Le
lignes AB, BC, CD, DA sont
donnés aussi bien que les angles PEB, PFC, PGC, PHD et l'on
demande que ![]() soit donné. Mais cette fois Newton ne mène pas
une ligne par un sommet du quadrilatère. Il choisit une
ligne arbitraire MI et il cherche un point P sur cette ligne. Les
rapports
soit donné. Mais cette fois Newton ne mène pas
une ligne par un sommet du quadrilatère. Il choisit une
ligne arbitraire MI et il cherche un point P sur cette ligne. Les
rapports
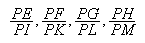
sont donnés. Donc (en employant pour commodité un peu d'algèbre), on a aussi les rapports donnés
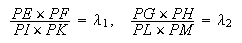 et
donc
et
donc 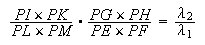
Mais le rapport ![]() est donné. Soit
est donné. Soit ![]() .
.
Il
s'ensuit que 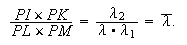
Nous sommes ramené au problème typique de la De sectione determinata. En termes modernes il s'agit simplement de résoudre une équation du second degré. [58] Encore une fois, Newton ne discute pas le fait qu'on a évidemment deux solutions.
Newton a toujours considéré le problème de Pappus comme équivalent à la détermination d'une conique par cinq points. Il a complètement ignoré l'existence de deux solutions peut-être en considérant le fait que le choix d'une région du plan conduit naturellement à la détermination d'une seule d'entre elles. Mais il n'a jamais explicité cette stratégie.
Toutefois ce problème lui a donné l'occasion de produire sa magistrale construction organique et, strictement connexe avec cette construction, la génération homographique des coniques.
Toutefois ces résultats, soit sont restés à l'état de manuscrits, soit ont été édités de manière inadéquate avant l'édition de Whiteside; ce qui ne leur a pas donné la possibilité d'avoir les conséquences mathématiques qui leur semblent inhérentes. En plus, la présentation des solutions du problème de Pappus comme la restauration de la « vraie mathématique » des Anciens a porté ombrage aux éléments novateurs. Si l'on regarde l'admirable Théorème 6, on voit que les éléments à l'infini ont un rôle considérable aussi bien que les relations bilinéaires. La connexion forcée aux mathématiques des Anciens a empêché ces travaux de trouver leur place propre dans le développement des mathématiques.