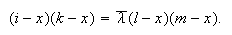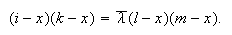
La référence aux Mathematical Papers édités par D.T. Whiteside sera donnée par le sigle MP, suivie de l'indication du volume et des pages.
Cf. (Galuzzi, 1990).
J'utilise la figure de la Géométrie de Descartes.
Qui ouvre la voie à la théorie algébrique moderne des sections coniques. Cf. (Galuzzi et Rovelli, Chapitre 2).
Cf. (Galuzzi et Rovelli, Section 2.4) et (Maronne, 2007, Chapitre 2).
Cf. (Turnbull, 1959, 229-234). Le texte est reproduit aussi dans (MP, p. 156-159). Dans la note 6 (p. 156-57) Whiteside observe justement que la figure dans le texte de Turnbull n'est pas reproduite exactement. Une analyse remarquable de cette construction est contenue dans (Guicciardini, 2009, Chapitre 5). Nous aurons occasion de nous confronter plusieurs fois avec ce livre très important que la courtoisie de l'auteur nous a permis de lire avant impression.
Cf. (MP, vol. 4, p. 282-321).
Cf. (MP, vol. 6, p. 242-299)
Cf. (Newton, 1687, p. 70-103).
Cf. (MP, vol. 4, p. 230-269). Newton connaissait le texte de Descartes par l'intermédiaire de la seconde traduction latine. Cf. (Descartes, 1659-61, p. 33-34).
Dans (MP, vol. 7) tous les matériaux qui devaient composer ce traité sont colligés.
Cf. (MP, vol. 4, p. 274-283).
Newton a toujours donné peu de relief au fait que la solution cartésienne est pour le cas général de 2n lignes et que le cas de quatre lignes est seulement un exemple dans La Géométrie.
Cf. (MP, vol. 4, p. 276). Le terme `lieu solide' est utilisé comme synonyme de conique. Une conique dans les mathématiques grecques est donnée par un cône (une figure dans l'espace) coupé par un plan: donc un lieu solide.
Dans le livre de (Guicciardini, 2009) on trouve une analyse raffinée de l'évolution des considérations méthodologiques qui après les années d'apprentissage viennent occuper un rôle de plus en plus remarquable dans la pensée de Newton.
Cf. (Newton, 1687, p. 70-103). Sur ce texte on peut voir aussi (Di Sieno et Galuzzi, 1989) et (Guicciardini, 2009, sections 5.3.2-5.4.6).
Mais l'édition est bien postérieure : (Newton, 1707).
Mais sur ce point il faut voir surtout (Guicciardini, 2009).
Une analyse remarquable des résultats de Newton sur les coniques est donnée dans (Milne, 1927). Naturellement Milne ne pouvait disposer des textes édités par Whiteside, ce qui rend son article encore plus considérable.
Dans (Heath, 1896, p. 95-98) on a une synthèse claire des résultats d'Apollonius.
Chasles observe (cf. (Chasles, 1875, p. 72) que cette proposition peut être obtenue comme cas particulier du théorème sur le quadrilatère dans l'Essai pour les coniques de Pascal. Voir (Pascal 1963, p. 36). Dans les Mathematical Papers il y a plusieurs lieux où Whiteside suggère un lien avec l'œuvre de Pascal. Cf. ( MP, vol. 2, p. 190-91, et p. 191 note 5) et surtout (MP, vol. 4, p. 321, note 90). On peut voir aussi (Taton, 1978).
Voir la Note 6. Voir (Milne, 1927, p. 109-110).
Cf. (MP, vol.2, p. 156-159. J'ai considéré aussi la traduction française du Madame du Châtelet du texte correspondant dans les Principia : cf. (Newton, 2005, p. 65-66). Voir aussi (MP, vol. 2, p. 158).
Cf. (MP, vol. 4, p. 236).
Cette démonstration nous semble plus simple que celle suggérée par Whiteside : cf. (MP, vol. 4, p. 236, note 6).
Cf. (MP, vol. 4, p. 274-283). Une analyse intéressante de ce texte est donné aussi dans (Sergio, 2006, Chapitre 7).
Comme Whiteside l'observe dans la Note 12 à la page 278.
Naturellement, si MN et PQ sont parallèles, nous avons le cas de la parabole. Voir (MP, vol. 4, note 17, p. 280) où Whiteside discute ce cas.
Cf. (MP, vol. 4, p. 280).
Voir la Note 1.
Une analyse de ce texte se trouve aussi dans (Guicciardini, 2009, Chapitre 5). Une analyse des propositions correspondantes contenues dans les Principia est dans (Milne, 1927, p. 102-114).
Cf. (MP, vol. 4, p. 282-284). L'énoncé est reproduit avec des différences minimales dans (Newton, 1687, p. 70). J'ai tenu compte pour ma traduction de celle de Madame du Châtelet : (Newton, 2005, p. 60).
Whiteside, dans (MP, vol. 4, p. 286-287, note 6) observe à la fin de la démonstration du deuxième cas que l'égalité des rapports «... set in modern cross-ratio form yields the homographic definition of the conic (D) through A, B, C and P by C(PDdA) = (PRr∞) = (PTt∞) = B(PDdA) ». Toutefois il ne considère pas le fait que A, B, C, P, d ne sont pas des points arbitraires, comme dans la Proposition 5.
Il faut voir la Figure 11 pour comprendre ce que Newton entend par `inscrit'.
Cf. (MP, vol. 4, p. 290-92) et (Newton, 1687, p. 75-76), (Newton, 2005, p. 64-65).
Cf. (MP, vol. 4, p. 288-290). Voir aussi (MP, vol. 6, p. 250-252) et (Newton, 1687, p. 74-75).
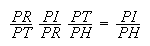
Cf.(MP, vol. 4, p. 294). Voir aussi (MP, vol. 6, p. 256-261) et (Newton, 1687, p. 79-81).
La proportion PR : PT = Pr : Pt peut se changer en PR : Pr = PT : Pt, qui signifie, en termes de rapport anharmonique, que :
(PRr∞)=(PTt∞)
Les faisceaux des lignes centrés en B et C qui projettent le point variable d sont projectifs.
Cf. (MP, vol. 4, p. 298-303). Voir aussi (MP, vol. 6, p. 254-57) et (Newton, 1687, p. 77-79).
Cf. (MP, vol. 4, p. 299, note 32).
Dans le manuscrit Newton utilise la même figure.
On peut voir l'explication très claire de Whiteside : cf. (MP, vol. 4, p. 298, note 30).
Par un procédé semblable à celui employé dans la Section 3.
Une démonstration algébrique de la construction organique est donnée dans (MP, vol. 5, p. 304-306). Une première tentative infructueuse est dans (MP, vol. 2, p. 152-55). Cf. (Guicciardini, 2009, Chapitre 5). On peut voir aussi (Whiteside, 1961).
Nous avons cette information par le célèbre memorandum de Gregory (ULE. Gregory C 42). Voir (MP, vol. 7, p. 196-197), où Whiteside en donne aussi une traduction anglaise. On peut voir aussi (Guicciardini, 1999, p. 179-184) et (Di Sieno et Galuzzi, 1989).
Sur ce point on peut voir l'Introduction de Whiteside à (MP, vol. 6).
Mais le Scholium ajouté au Lemme XVIII (correspondant à la Proposition 2 de la Solutio) manifeste, implicitement, puisque Descartes n'est pas nommé, l'intolérance de Newton envers l'exemple du cercle de Descartes. On peut voir aussi (Di Sieno et Galuzzi 1989).
Voir par exemple (MP, vol. 4, p. 294, Prop. 6) et (Newton, 1687, p. 79, Prop. XXII).
C'est à dire que ces longueurs sont données par une relation bilinéaire. Voir la note 51.
Cf. (MP, vol. 4, p. 308-313).
Soit PR = x, PT = y. On a donc à une relation de la forme αxy + βx + γy + δ=0, où α, β, γ, δ sont des constantes.
Donc on doit avoir δ=0.
On doit avoir α = 0.
Cf. (Newton, 1707, p. 215) et Cf. (MP, vol. 5, p. 314). En fait dans sa solution du Problema astronomicun (cf. (Newton, 1707, p. 182-189) et (MP, vol. 5, p. 266-279) on trouve l'utilisation de l'équation d'une section conique de la forme aa⊥bx⊥cxx = yy (où⊥ est utilisé pour ±) de façon semblable. Mais ici les outils de l'algèbre sont assimilables à l'idée de l'analyse des Anciens et n'ont pas un relief théorique autonome. Sur les différentes solutions du Problema astronomicum on peur voir l'intéressante analyse donnée dans (Maronne, 2007, Partie III).
Ibid.
On peut en trouver une exposition détaillée et profonde dans (Guicciardini, 2009).
Ou peut être par la reconstruction dans l'Apollonius redivivus de Anderson (Paris, 1612).
En termes de coordonnées : I = (i), K = (k), L = (l), M = (m) et, en posant P
= (x) ,
on a