|
|
Mathématiques de la musique en Afrique centrale
Marc ChemillierDirecteur d'études à l'École des Hautes Études en Sciences Sociales (EHESS) - email
Cet article est une version augmentée d'un texte paru dans le Dossier spécial du magazine Pour la Science intitulé " Mathématiques exotiques " (avril-juin 2005).
La version proposée par CultureMATH est différente de celle de Pour la Science: l'iconographie a été augmentée, la mise en page est plus sobre, mais le texte est sur certains points, plus complet. Trois séquences musicales illustrent le propos de l'auteur.
Toute reproduction
pour publication ou à des
fins commerciales, de la totalité ou d'une partie de
l'article, est interdite. Toute
reproduction à des fins strictement
pédagogiques dans le cadre limité d'une
formation, de la totalité ou
d'une partie de l'article, est autorisée sous
réserve d'un accord
préalable de l'éditeur
(ENS Ulm) et de la mention
explicite des références éditoriales
de l'article.
 |
|
|
SOMMAIRE
1. Introduction
2. Formules de la harpe nzakara "en canon" 3. Rythmes asymétriques africains (d’après Simha Arom) 4. Symétries des formules de harpe nzakara 5. Bibliographie Encart
Equivalence de la structure « en escalier » et de la structure de canon Figures
Figure 1: Sculpture de tête sur le manche d'une harpe zandé - Harpe mangbetu Figure 2: Le chef nzakara Mada Nyalikawo accompagne à la harpe l’une de ses épouses qui chante. Figure 3: Formules de harpe nzakara en canon Figure 4: L’étoile à cinq branches indiquant les couples de cordes pincées simultanément Figure 5: Graphe d’enchaînement à distance du canon pour les couples de cordes jouées simultanément Figure 6: Structure en escalier Figure 7: Polyphonie vocale et instrumentale des Pygmées Aka Figure 8: Une formule rythmique asymétrique Figure 9: Représentation d'une séquence rythmique pygmée Figure 10: Pygmées Aka frappant la formule rythmique mokongo Figure 11: Symétries centrales d'une formule de harpe nzakara Liens vers des documents en ligne Séquences
musicales
- Une formule de harpe nzakara en canon - Une formule asymétrique extraite de la pièce mbenzele des Pygmées Aka - Rythme mokongo frappé par 2 musiciens Pygmées aka |
Dans
la tradition musicale savante occidentale (et cela vaut aussi pour les
traditions savantes non occidentales comme la tradition chinoise), la
musique a toujours été associée aux
mathématiques. Dans le contexte de
sociétés sans écriture, en revanche,
cette association peut paraître plus surprenante. Le but de
cet article est de montrer quelques cas de répertoires
musicaux de tradition orale dans lesquels on peut mettre en
évidence des structures musicales complexes comparables
à des constructions mathématiques. Ces exemples
ouvrent un champ d'étude nouveau et important aux recherches
en ethnomathématique, qui ont porté
jusqu'à présent plutôt sur les arts
visuels tels que la décoration (symétrie de
figures ornementales, topologie de tracés
linéaires), leurs propriétés formelles
étant plus facilement « visibles » que
les propriétés par essence « invisibles
» de la musique.
Formules de harpe nzakara « en canon »
Les Nzakara et Zandé,
apparentés par leurs
langues, occupent un territoire réparti entre la
République centrafricaine, le Congo (ex-Zaïre) et
le Soudan. Ils formaient au XIXe siècle de
véritables royaumes, et les anciennes traditions musicales
nzakara et zandé semblent avoir été
largement tributaires de cette organisation politique originale.
Certains aspects de ces traditions, comme l’usage de la harpe
à cinq cordes, sont sans doute communs à toute
l’aire culturelle nzakara-zandé. Les
poètes-musiciens accompagnaient jadis leur chant
à l’aide de formules traditionnelles
jouées sur cet instrument. On peut admirer les beaux
exemplaires anciens conservés dans les musées,
qui sont ornés de magnifiques têtes
sculptées (voir la figure 1). Au-delà de ces
aspects généraux, il existait probablement des
traits spécifiques aux répertoires musicaux des
différents royaumes, mais les informations sont
insuffisantes pour permettre une étude comparative. Nous
avons effectué des recherches sur certaines formules de
harpe particulières en usage dans l’ancien royaume
Nzakara de la région de Bangassou, à
l’est de la République centrafricaine, qui ont
révélé des structures remarquables.
|
Figure 1
  (a) Tête sculptée d'un harpe zandé (acquise par Marcel Dumoulin - Collections du Musée royal de l'Afrique centrale, Tervuren (n° inv. 58.13.9). Reproduction d'un cliché possession du Laboratoire d'ethnologie et de sociologie comparative(UMR 7186, CNRS- Université Paris Ouest). (b) Harpe mangbetu (République Démocratique du Congo). © musée du quai Branly. |
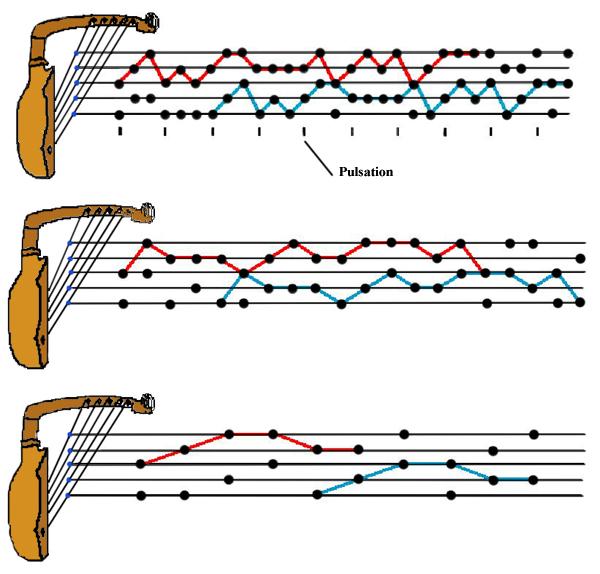
Les formules de harpe sont répétées en boucle pour accompagner une improvisation poétique chantée. La harpe est tenue verticalement (voir la figure 2), et les cordes sont pincées par couples (une corde par chaque main). Le rythme de ces formules est régulier, et il s’appuie sur une pulsation sous-jacente, c’est-à-dire un découpage du temps en unités égales qui est généralement sous-entendu, mais qui est parfois matérialisé par des frappements de mains ou des battements de grelots winga.
|
Figure 2
 Le chef nzakara Mada Nyalikawo
accompagne à la harpe l’une de ses
épouses qui chante en frappant dans ses mains (couverture du
disque Musiques des anciennes cours Bandia, collection
CNRS/Musée de l’Homme, 1996, photo Marc Chemillier). ECOUTER
|
Parmi
les formules traditionnelles nzakara, il
existe un sous-ensemble
de formules qui ont la propriété remarquable
d'être des canons. La figure 3 montre la transcription de
certaines de ces formules. Les cinq lignes horizontales correspondent
aux cinq cordes de l'instrument. Les points indiquent quelles cordes
sont pincées pendant le déroulement de la
formule. Les cordes pincées par couples forment deux lignes
mélodiques superposées, l'une sur les trois
cordes aiguës et l'autre sur les trois cordes graves. On
constate qu'à quelques exceptions près, leurs
deux profils mélodiques sont identiques, mais
décalés dans le temps. Il s’agit donc
d’un canon,
dans un sens proche de celui de la musique occidentale. Les deux voix
canoniques sont matérialisées sur la
transcription par des lignes zigzagantes bleues et rouges. Notons que
ce tracé fait apparaître quelques «
erreurs », c’est-à-dire des exceptions
à la règle du canon indiquées par les
points sur la corde la plus grave qui sont extérieurs
à la ligne bleue. La distance
du canon est le nombre de couples qui séparent le
début de la voix grave de celui de la voix aiguë
(la distance a pour valeurs respectivement 6, 4 et 4 dans les trois
formules de la figure 3). Au décalage près de la
distance du canon, cette voix suit le même profil
mélodique, mais elle est transposée sur des
cordes plus graves, qui sont à un intervalle fixe
des cordes de la voix aiguë (la valeur de cet intervalle est
deux cordes).
Si l'on formalise
mathématiquement le problème de
la construction de tels canons, on constate la
propriété suivante : il est impossible de fabriquer
une séquence de harpe qui soit un canon au sens strict
(c'est-à-dire sans aucune exception dans la reproduction par
une voix du profil mélodique de l'autre). Cette
impossibilité est une conséquence du fait que
l’on doit concilier deux contraintes incompatibles, une
contrainte « horizontale » qui est
imposée par l'identité des profils
mélodiques, et une contrainte « verticale
» qui interdit certains couples de cordes
simultanées. En effet, dans le répertoire nzakara
illustré par ces formules de harpe, les cordes qui sont
placées côte à côte sur
l’instrument ne sont jamais jouées ensemble, et il
en est de même pour les cordes extrêmes. Si
l’on dispose les cinq cordes de la harpe sur un cercle, en
joignant celles qui peuvent être pincées
simultanément, on obtient une figure
géométrique complète et
symétrique, en forme d’«
étoile » à cinq branches.
La structure de canon implique que dans une formule de harpe, les couples de cordes simultanées qui sont à une distance donnée (celle du canon) satisfont une relation particulière. Cette relation, qui assure globalement la reproduction par la voix grave du profil mélodique de la voix aiguë, s’exprime localement au niveau des enchaînements d’un couple à un autre. La corde la plus grave du deuxième couple doit être à intervalle fixe de la corde la plus aiguë du premier. Si l’on numérote 0, 1, 2, 3, 4 les cinq couples de cordes jouées simultanément (en commençant par le grave, c’est-à-dire que 0 désigne le couple formé par la corde la plus grave et la corde du milieu), la relation d’enchaînement d’un couple à un autre à distance du canon se traduit par un graphe (voir la figure 5). Notons qu’on a rajouté une flèche supplémentaire dans ce graphe (de 4 vers 0), qui ne correspond pas à la règle du canon. Mais cet enchaînement est utilisé effectivement par les musiciens nzakara dans leurs formules de harpe, et c’est lui qui produit ce que nous avons appelé plus haut des « erreurs », c’est-à-dire des points où la voix grave ne suit pas la voix aiguë.
L'analyse formelle du problème de la construction des canons montre qu'un canon comporte nécessairement certaines erreurs. Cela résulte du fait que l’on doit parcourir un cycle dans le graphe de la figure 5, et qu’un tel cycle passe nécessairement par la flèche en pointillée responsable d’une anomalie dans la structure de canon (sauf si on utilise un cycle « trivial » consistant à répéter indéfiniment le même couple). Un raisonnement plus détaillé permet de montrer que le nombre minimal d’erreurs dans un canon sans cycles triviaux est égal au pgcd(n, p), où n est la longueur de la séquence, et p la distance du canon. Les canons nzakara ont toujours le nombre minimal d'erreurs (on peut le vérifier facilement pour ceux de la figure 3, en comptant les erreurs, sachant que les valeurs de n sont respectivement 30, 20 et 10, et celles de p 6, 4 et 4).
L'analyse que nous venons de décrire brièvement ne tient pas compte de la manière dont les Nzakara se représentent eux-mêmes leurs formules de harpe, et lorsque nous parlons d'« interdiction » ou d'« erreurs » dans la structure de canon, ces termes n'ont évidemment qu'une valeur métaphorique. Le problème est très différent, en revanche, si l'on se place sur le plan cognitif, c'est-à-dire sur celui des représentations mentales autochtones. Les Nzakara ignorent-ils les propriétés de ces formules, ou bien sont-ils conscients de la structure de canon, c'est-à-dire de l'identité des deux profils mélodiques ? Nous ne pouvons répondre directement à cette question, et dans un article de la revue L'Homme, nous avons exposé cette problématique, en soulignant les difficultés qu'il y avait à ancrer dans la réalité cognitive autochtone certaines analyses abstraites. La plupart des études d'ethnomathématique abordent les propriétés formelles des systèmes étudiés indépendamment des processus mentaux effectivement mis en œuvre par ceux qui sont à l’origine de ces systèmes. L’une des principales raisons est que les études sont menées a posteriori, à partir de données de terrain recueillies en dehors de toute préoccupation mathématique. C’est le cas de notre étude des canons nzakara, qui manque d’informations sur la manière dont les musiciens de cette société se représentent leurs propres formules instrumentales. Nous avons proposé un faisceau d'indices, tirés de nos travaux menés en collaboration avec l'ethnologue Éric de Dampierre, spécialiste de la société nzakara, qui pourraient expliquer l'apparition de ces formules en canon. L’un des principaux arguments en faveur de cette hypothèse est l’utilisation par les Nzakara d’une plante particulière dans le rituel des jumeaux. La géométrie remarquable de cette plante, dont les deux rangées de feuilles sont dans deux plans perpendiculaires, et décalées l’une par rapport à l’autre le long de la tige, explique pourquoi elle intervient dans ce rituel. Il est donc possible que l’intérêt des Nzakara pour la géométrie de cette plante soit en relation avec une intention supposé des musiciens de jouer des formules en canon, c’est-à-dire ayant deux lignes mélodiques décalées. Mais la question est controversée, et l'ethnomusicologue Klaus-Peter Brenner a publié un livre, dans lequel il rejette l'hypothèse des canons, et développe l'idée que sur le plan cognitif, les formules nzakara doivent être analysées autrement.
Il est possible en effet d'analyser les formules nzakara d'une manière totalement différente, quoique logiquement équivalente. Si l'on numérote tous les couples de cordes successifs dans les formules de la figure 3 (en adoptant la numérotation de 0 à 4 ci-dessus), on fait alors apparaître une structure « en escalier ». Par exemple, dans la première formule, les six premiers couples 023010 sont ensuite décalés d'une unité 134121, et ainsi de suite, jusqu'à revenir à la succession initiale (voir la figure 6). La structure en escalier consiste à translater un motif initial autant de fois qu'il le faut pour revenir au point de départ. On peut montrer que sous certaines conditions, cette structure en escalier est logiquement équivalente à la structure de canon. En effet, il est facile de voir que si la numérotation des couples est celle définie par le graphe de la figure 5, alors une formule en escalier est nécessairement un canon (dont la distance est la longueur du motif translaté). Inversement, si un canon est construit en utilisant uniquement le cycle 0 → 1→ 2→ 3→ 4→ 0 du graphe de la figure 5 (sans cycles triviaux), alors il possède nécessairement une structure en escalier. (Lire la démonstration.)
La structure en escalier conduit à mettre en évidence une propriété supplémentaire remarquable d'unicité concernant la plus courte des formules de la figure 3 (c’est-à-dire la deuxième figure 6). Ici, le motif translaté 01 ne contient que deux couples et la translation est de 3 unités (modulo 5). On peut alors se demander combien il est possible de fabriquer de séquences de ce type à partir d'un motif ayant seulement deux couples. Fixons le premier couple à 0, et énumérons les valeurs possibles pour le second. Si l'on prend 0, le motif translaté serait 00. On obtiendrait alors une répétition de couples, ce qui ne se produit jamais dans les formules du répertoire nzakara. Si l'on prend 1, le résultat est la formule de la figure 3. Si l'on prend 2, on remarque que la formule obtenue n'est qu'une permutation circulaire de la précédente. Si l'on prend 3, on obtient de nouveau une répétition de couples 33. Enfin, si l'on prend 4, on constate que la formule se scinde en deux (04321 est répété deux fois). On voit que pour les valeurs 0, 3, 4, la séquence obtenue est en quelque sorte « dégénérée » (répétition d'un couple, ou répétition d'une séquence plus courte), et que pour les autres valeurs 1 et 2, on obtient la même séquence à une permutation circulaire près. Finalement, la formule nzakara apparaît comme la seule manière possible de fabriquer une séquence en escalier à partir d'un motif ayant seulement deux couples.
|
Figure 4
 Les cinq cordes
disposées en cercle, et
l’étoile à cinq branches indiquant les
couples de cordes pincées simultanément.
|
La structure de canon implique que dans une formule de harpe, les couples de cordes simultanées qui sont à une distance donnée (celle du canon) satisfont une relation particulière. Cette relation, qui assure globalement la reproduction par la voix grave du profil mélodique de la voix aiguë, s’exprime localement au niveau des enchaînements d’un couple à un autre. La corde la plus grave du deuxième couple doit être à intervalle fixe de la corde la plus aiguë du premier. Si l’on numérote 0, 1, 2, 3, 4 les cinq couples de cordes jouées simultanément (en commençant par le grave, c’est-à-dire que 0 désigne le couple formé par la corde la plus grave et la corde du milieu), la relation d’enchaînement d’un couple à un autre à distance du canon se traduit par un graphe (voir la figure 5). Notons qu’on a rajouté une flèche supplémentaire dans ce graphe (de 4 vers 0), qui ne correspond pas à la règle du canon. Mais cet enchaînement est utilisé effectivement par les musiciens nzakara dans leurs formules de harpe, et c’est lui qui produit ce que nous avons appelé plus haut des « erreurs », c’est-à-dire des points où la voix grave ne suit pas la voix aiguë.
|
Figure 5
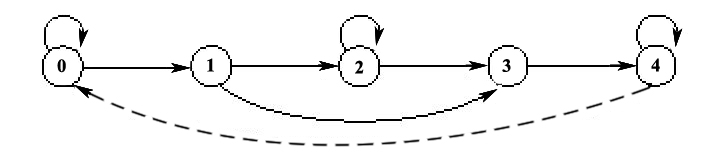 Graphe
d’enchaînement à
distance du canon pour les couples de cordes jouées
simultanément.
|
L'analyse formelle du problème de la construction des canons montre qu'un canon comporte nécessairement certaines erreurs. Cela résulte du fait que l’on doit parcourir un cycle dans le graphe de la figure 5, et qu’un tel cycle passe nécessairement par la flèche en pointillée responsable d’une anomalie dans la structure de canon (sauf si on utilise un cycle « trivial » consistant à répéter indéfiniment le même couple). Un raisonnement plus détaillé permet de montrer que le nombre minimal d’erreurs dans un canon sans cycles triviaux est égal au pgcd(n, p), où n est la longueur de la séquence, et p la distance du canon. Les canons nzakara ont toujours le nombre minimal d'erreurs (on peut le vérifier facilement pour ceux de la figure 3, en comptant les erreurs, sachant que les valeurs de n sont respectivement 30, 20 et 10, et celles de p 6, 4 et 4).
L'analyse que nous venons de décrire brièvement ne tient pas compte de la manière dont les Nzakara se représentent eux-mêmes leurs formules de harpe, et lorsque nous parlons d'« interdiction » ou d'« erreurs » dans la structure de canon, ces termes n'ont évidemment qu'une valeur métaphorique. Le problème est très différent, en revanche, si l'on se place sur le plan cognitif, c'est-à-dire sur celui des représentations mentales autochtones. Les Nzakara ignorent-ils les propriétés de ces formules, ou bien sont-ils conscients de la structure de canon, c'est-à-dire de l'identité des deux profils mélodiques ? Nous ne pouvons répondre directement à cette question, et dans un article de la revue L'Homme, nous avons exposé cette problématique, en soulignant les difficultés qu'il y avait à ancrer dans la réalité cognitive autochtone certaines analyses abstraites. La plupart des études d'ethnomathématique abordent les propriétés formelles des systèmes étudiés indépendamment des processus mentaux effectivement mis en œuvre par ceux qui sont à l’origine de ces systèmes. L’une des principales raisons est que les études sont menées a posteriori, à partir de données de terrain recueillies en dehors de toute préoccupation mathématique. C’est le cas de notre étude des canons nzakara, qui manque d’informations sur la manière dont les musiciens de cette société se représentent leurs propres formules instrumentales. Nous avons proposé un faisceau d'indices, tirés de nos travaux menés en collaboration avec l'ethnologue Éric de Dampierre, spécialiste de la société nzakara, qui pourraient expliquer l'apparition de ces formules en canon. L’un des principaux arguments en faveur de cette hypothèse est l’utilisation par les Nzakara d’une plante particulière dans le rituel des jumeaux. La géométrie remarquable de cette plante, dont les deux rangées de feuilles sont dans deux plans perpendiculaires, et décalées l’une par rapport à l’autre le long de la tige, explique pourquoi elle intervient dans ce rituel. Il est donc possible que l’intérêt des Nzakara pour la géométrie de cette plante soit en relation avec une intention supposé des musiciens de jouer des formules en canon, c’est-à-dire ayant deux lignes mélodiques décalées. Mais la question est controversée, et l'ethnomusicologue Klaus-Peter Brenner a publié un livre, dans lequel il rejette l'hypothèse des canons, et développe l'idée que sur le plan cognitif, les formules nzakara doivent être analysées autrement.
Il est possible en effet d'analyser les formules nzakara d'une manière totalement différente, quoique logiquement équivalente. Si l'on numérote tous les couples de cordes successifs dans les formules de la figure 3 (en adoptant la numérotation de 0 à 4 ci-dessus), on fait alors apparaître une structure « en escalier ». Par exemple, dans la première formule, les six premiers couples 023010 sont ensuite décalés d'une unité 134121, et ainsi de suite, jusqu'à revenir à la succession initiale (voir la figure 6). La structure en escalier consiste à translater un motif initial autant de fois qu'il le faut pour revenir au point de départ. On peut montrer que sous certaines conditions, cette structure en escalier est logiquement équivalente à la structure de canon. En effet, il est facile de voir que si la numérotation des couples est celle définie par le graphe de la figure 5, alors une formule en escalier est nécessairement un canon (dont la distance est la longueur du motif translaté). Inversement, si un canon est construit en utilisant uniquement le cycle 0 → 1→ 2→ 3→ 4→ 0 du graphe de la figure 5 (sans cycles triviaux), alors il possède nécessairement une structure en escalier. (Lire la démonstration.)
|
Figure 6: Structure en escalier.
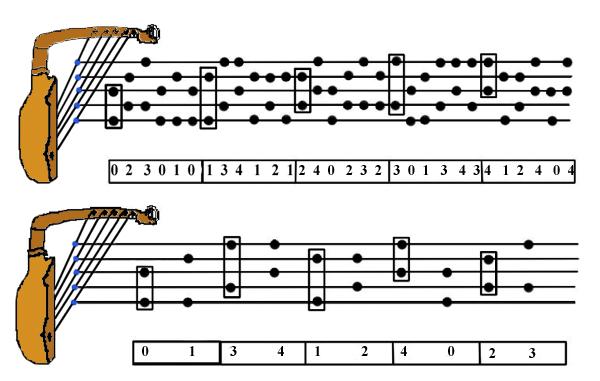 |
La structure en escalier conduit à mettre en évidence une propriété supplémentaire remarquable d'unicité concernant la plus courte des formules de la figure 3 (c’est-à-dire la deuxième figure 6). Ici, le motif translaté 01 ne contient que deux couples et la translation est de 3 unités (modulo 5). On peut alors se demander combien il est possible de fabriquer de séquences de ce type à partir d'un motif ayant seulement deux couples. Fixons le premier couple à 0, et énumérons les valeurs possibles pour le second. Si l'on prend 0, le motif translaté serait 00. On obtiendrait alors une répétition de couples, ce qui ne se produit jamais dans les formules du répertoire nzakara. Si l'on prend 1, le résultat est la formule de la figure 3. Si l'on prend 2, on remarque que la formule obtenue n'est qu'une permutation circulaire de la précédente. Si l'on prend 3, on obtient de nouveau une répétition de couples 33. Enfin, si l'on prend 4, on constate que la formule se scinde en deux (04321 est répété deux fois). On voit que pour les valeurs 0, 3, 4, la séquence obtenue est en quelque sorte « dégénérée » (répétition d'un couple, ou répétition d'une séquence plus courte), et que pour les autres valeurs 1 et 2, on obtient la même séquence à une permutation circulaire près. Finalement, la formule nzakara apparaît comme la seule manière possible de fabriquer une séquence en escalier à partir d'un motif ayant seulement deux couples.
| Répétition de couples | 0033114422 |
| Formule nzakara | 0134124023 |
| Permutation de la formule nzakara | 0230134124 |
| Répétition de couples | 0331144220 |
| Répétition d'une séquence plus courte | 0432104321 |
Rythmes asymétriques africains (d’après Simha Arom)
Nous
allons présenter un deuxième exemple de
structure mathématique apparaissant dans les
répertoires musicaux d'Afrique centrale, qui concerne cette
fois la dimension rythmique. Il s’agit d’une
structure rythmique asymétrique, qui est
utilisée, entre autres, par les Pygmées Aka, un
peuple de chasseurs-cueilleurs vivant dans la forêt
tropicale, au sud-ouest de la République centrafricaine,
dans la vallée de la Lobaye.
Ces rythmes africains ont un aspect asymétrique caractéristique, obtenu en combinant des durées de 2 et 3 unités. Les polyphonies vocales et instrumentales très complexes des Pygmées Aka comportent quelques uns de ces rythmes, comme celle illustrées par la figure 7.
À l’intérieur de cette polyrythmie, il existe une formule asymétrique, qui est soulignée dans la transcription par des rectangles oranges, et jouée avec des lames entrechoquées de machettes en fer. On observe que certains rectangles oranges sont plus proches de celui qui précède que les autres. Si on les regroupe avec leur prédécesseur, on forme ainsi des durées de trois unités, qui viennent s'insérer dans une succession de durées de deux unités. La formule rythmique, qui est répétée en boucle, peut ainsi s'écrire 22222322223 (voir la figure 8).
Les rythmes asymétriques de ce type qu'on trouve en Afrique centrale ont une propriété particulière appelée imparité rythmique, qui a été mise en évidence par l'ethnomusicologue Simha Arom, et qui s'exprime naturellement sous la forme d'un énoncé mathématique. En représentant la séquence rythmique précédente sur un cercle (voir la figure 9), la propriété exprime le fait qu'on ne peut couper le cercle en deux parties égales quelque soit le point choisi.
Nous avons proposé une construction permettant d'obtenir de proche en proche tous les rythmes satisfaisant cette propriété d'imparité rythmique. Pour tout couple (u, v) de mots formés de 2 et de 3, on fabrique deux nouveaux couples de mots, selon deux transformations différentes (que nous noterons a et b) :
Ces rythmes africains ont un aspect asymétrique caractéristique, obtenu en combinant des durées de 2 et 3 unités. Les polyphonies vocales et instrumentales très complexes des Pygmées Aka comportent quelques uns de ces rythmes, comme celle illustrées par la figure 7.
|
Figure 7
 Polyphonie vocale et instrumentale des Pygmées Aka dans la pièce mbenzele (transcription extraite du cédérom Pygmées Aka, peuple et musique, réalisé par l'équipe de Simha Arom, Montparnasse multimédia, 1999). L’axe horizontal est l’axe du temps. Les deux lignes du bas représentent une polyrythmie instrumentale (les instruments sont symbolisés par des carrés, rectangles, ou triangles). Au-dessus, les lignes brisées de couleur verte, rouge, marron, et jaune représentent les motifs mélodiques chantés par quatre voix. |
À l’intérieur de cette polyrythmie, il existe une formule asymétrique, qui est soulignée dans la transcription par des rectangles oranges, et jouée avec des lames entrechoquées de machettes en fer. On observe que certains rectangles oranges sont plus proches de celui qui précède que les autres. Si on les regroupe avec leur prédécesseur, on forme ainsi des durées de trois unités, qui viennent s'insérer dans une succession de durées de deux unités. La formule rythmique, qui est répétée en boucle, peut ainsi s'écrire 22222322223 (voir la figure 8).
|
Figure 8
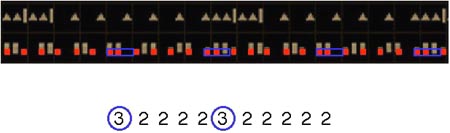 Formule asymétrique jouée avec des lames entrechoquées de machettes en fer. ECOUTER - Enregistrement Simha Arom |
Les rythmes asymétriques de ce type qu'on trouve en Afrique centrale ont une propriété particulière appelée imparité rythmique, qui a été mise en évidence par l'ethnomusicologue Simha Arom, et qui s'exprime naturellement sous la forme d'un énoncé mathématique. En représentant la séquence rythmique précédente sur un cercle (voir la figure 9), la propriété exprime le fait qu'on ne peut couper le cercle en deux parties égales quelque soit le point choisi.
|
Figure 9
 Rythme 32222322222 non
divisible en deux parties de
même
durée.
Image animée |
Nous avons proposé une construction permettant d'obtenir de proche en proche tous les rythmes satisfaisant cette propriété d'imparité rythmique. Pour tout couple (u, v) de mots formés de 2 et de 3, on fabrique deux nouveaux couples de mots, selon deux transformations différentes (que nous noterons a et b) :
|
Transformation a
|
Transformation b | |||||
| u | → | 3u | u | → | v | |
| v | → | 3v | v | → | 2u | |
On peut montrer mathématiquement que les séquences vérifiant l'imparité rythmique sont exactement celles qu'on fabrique en mettant bout à bout deux mots u et v obtenus en appliquant un nombre quelconque de fois les transformations a et b à partir du couple de mots vides, à condition que b soit appliquée un nombre impair de fois. Par exemple, la suite de transformations abbb donne le mot 32322, comme on peut le vérifier étape à étape :
| b | b | b | a | |||||
| Vide | → | Vide | → | 2 | → | 2 | → | 32 |
| Vide | → | 2 | → | 2 | → | 22 | → | 322 |
et cette séquence 32322 satisfait la propriété d'imparité rythmique.
Quand on effectue la construction de toutes les formules rythmiques possibles de petite longueur, on s'aperçoit que les solutions sont peu nombreuses, et que si on leur impose de satisfaire de surcroît un trait caractéristique des formules en usage dans la région, alors elles sont pratiquement toutes utilisées, par les Pygmées Aka ou par d’autres populations voisines (Zande, Gbaya, Nzakara, Ngbaka). Ce trait concerne la somme totale des durées présentes dans la séquence, qui est toujours choisi parmi les valeurs 8, 12, 16 ou 24 (c'est-à-dire de la forme 2a ou 2a x 3). En restreignant le calcul aux séquences de ce type, et en éliminant de plus celles qui sont la répétition d'une séquence plus courte, on obtient le tableau suivant où n3, n2 désignent respectivement les nombres de 3 et de 2 de la séquence :
|
n3 |
n2 |
Somme | Transformations | Rythme | Groupe ethnique |
| 2 | 1 | 8 | ab | 332 | Zande |
| 3 | 12 | abbb | 32322 | Aka, Gbaya, Nzakara | |
| 5 | 16 | abbbbb | 3223222 | Gbaya, Ngbaka | |
| 9 | 24 | abbbbbbbbb | 32222322222 | Aka | |
| 6 | 3 | 24 | aaabbb | 333233322 | séquence non utilisée |
| 24 | aababb | 333233232 | Aka (mokongo) | ||
| 24 | aabbab | 333232332 | rétrograde de la précédente |
On voit que pour n3 = 2, les séquences sont toutes utilisées. Pour n3 = 6, deux séquences parmi les trois obtenues sont rétrogrades l'une de l'autre, ce qui signifie que chacune s’obtient en lisant l’autre en sens inverse (de la droite vers la gauche). L'une de ces deux formes est utilisée par les Pygmées Aka. Il s’agit de la formule rythmique 333233232 appelée mokongo, qui est frappée sur une poutre de bois (voir le figure 10). Elle intervient dans le rituel du zoboko effectué la veille d'une grande chasse. En fin de compte, dans le tableau ci-dessus, il ne reste qu'une seule séquence théoriquement possible 333233322 qui, pour des raisons inconnues, n’est pas attestée dans les répertoires de la région.
|
Figure 10
 Pygmées Aka
frappant la formule rythmique mokongo 333233232
ECOUTER : rythme
mokongo,
frappé par 2 musiciens Pygmées aka.
Enregistrement Simha Arom
|
Cette énumération conduit à penser qu'il y a des raisons d'ordre cognitif qui expliquent l'apparition de ces formules rythmiques. Mais la question reste difficile à trancher, en l'absence de discours réflexif des musiciens eux-mêmes sur leur pratique. Dans le cas des formules de harpe nzakara en canon étudiées précédemment, on a vu que les problèmes d'ordre cognitif sont les mêmes, faute d'un discours autochtone sur les propriétés de la musique. En particulier, aucun terme vernaculaire ne permet de caractériser spécifiquement les formules de harpe qui sont des canons. Mais on peut utiliser le même type d'argument combinatoire que pour les rythmes asymétriques. En effet, la structure de canon nzakara apparaît dans un groupe de six formules du répertoire des harpistes. Or celui-ci comporte une trentaine de formules connues, ce qui conduit à une proportion de 20 % de formules ayant la structure étudiée. Certes, ces formules sont minoritaires dans le corpus, mais leur proportion est cependant largement supérieure à celle qu'on obtiendrait si aucun facteur ne favorisait l'apparition de telles formules. Ainsi, lorsqu'une propriété n'apparaît pas de façon accidentelle ou casuelle, on est conduit à supposer que des conditions psychologiques particulières favorisent son apparition. D'où l'hypothèse d'une représentation mentale expliquant l'existence de ces formules en canon (ou en escalier, si l'on préfère adopter ce point de vue logiquement équivalent, comme on l'a vu plus haut).
Symétries des formules de harpe nzakara
Certaines formules de harpe nzakara en canon ont
une
propriété remarquable supplémentaire,
mais pour
laquelle on ne peut invoquer l'argument combinatoire ci-dessus, comme
on va le voir plus loin. Cette propriété a
été remarquée par le
mathématicien Dave
Benson, et elle fait intervenir la notion de groupe de frise. On sait
qu'il existe 230 différents types possibles de
symétrie
dans l’espace, et que la classification
mathématique de
tous les types a été établie au XIXe
par
Schönflies et Fédorov (elle était
motivée
à l’époque par les progrès
de la
cristallographie). Historiquement, cette classification a
été achevée avec l'apparition du
concept de
groupe. Un motif u
est dit symétrique
s'il existe une transformation T
qui laisse u
invariant T(u) = u.
L'ensemble des transformations laissant u invariant est
stable par
composition et forme donc un groupe, ce qui ramène
l'étude des symétries à un
problème de
classification de groupes. Dans le plan, on obtient 17 groupes de
symétrie, qui ont été
énumérés pour la première
fois en 1924 dans
une note du mathématicien Georges Pòlya, et si
l'on
suppose que les translations du groupe forment un réseau
à une seule dimension, alors il n'y a que 7 types possibles
de
symétries, qui correspondent aux sept groupes de frise.
Parmi les sept groupes de frise, le premier, noté p111 dans le système des cristallographes, est engendré par une translation. Le second, noté p112, est engendré par une translation et une symétrie centrale. On montre alors qu'il contient une infinité de symétries centrales, dont les centres sont équidistants. Plus précisément, la longueur de la translation est égale au double de la distance séparant deux centres de symétrie consécutifs.
La propriété remarquable de la première formule de harpe de la figure 3 est qu'elle est invariante par une symétrie centrale, c'est-à-dire que son groupe de symétrie est de type p112 (et non pas seulement p111). Pour placer le centre de symétrie en début de formule, décalons celle-ci de deux couples vers la droite (voir la figure 11). On remplace la numérotation des couples précédente, par une numérotation des cordes elles-mêmes, indiquée sous la figure, en notant de 0 à 4 les cordes du grave à l'aigu. Les centres de symétries sont alors matérialisés graphiquement par des petites croix. On a de plus relié par des traits les deux lignes invariantes par symétrie centrale. Ces tracés zigzagants donnent une image de la formule bien différente de celle utilisée figure 3 pour la mise en évidence du canon.
Pour vérifier la symétrie, on prend la première paire {1, 4} et la dernière {1, 3}. Leurs éléments peuvent être groupés par deux de telle sorte que la somme modulo 5 soit constante : 1 + 1 = 3 + 4 = 2. De même, lorsqu'on prend les autres paires, on trouve toujours la même somme constante égale à 2 quand on les associe à la paire en même position à partir de la fin.
Si la théorie des groupes de symétrie date du XIXe siècle, l’exploration des différents types de symétrie a commencé bien avant, dans les productions artistiques des civilisations non occidentales, et particulièrement dans leurs figures ornementales. L'utilisation des 17 types de symétrie plane est déjà manifeste dans les décorations de l’architecture arabe (mosaïque, carrelage). Il est généralement admis que la variété de symétries obtenues par les artistes arabes n'est pas le fruit du hasard, mais plutôt le résultat d'une recherche systématique ayant pour but d'obtenir la diversité la plus grande possible. Dans la musique également (mais cette fois, il s'agit de la musique occidentale), l'utilisation de la rétrogradation et de l'inversion est attestée depuis les temps les plus reculés. La question est donc posée de savoir si l'apparition de propriétés de ce type dans un répertoire musical de tradition orale s'inscrit dans le même processus cognitif.
Malheureusement, cette propriété de symétrie n'est pas vraie pour toutes les formules de harpe en canon du répertoire nzakara. On peut vérifier en effet que la deuxième formule de la figure 3 n'a pas de symétrie centrale. Dans ces conditions, l'argument combinatoire évoqué plus haut ne plaide pas en faveur d'une explication d'ordre cognitif à l'apparition de symétries centrales dans les fomules de harpe nzakara. D'un côté, il est remarquable qu'une formule admette ce type de symétrie, mais de l'autre, elle apparaît comme un cas particulier isolé, qui ne s'inscrit pas dans un processus mental d'exploration systématique.
Parmi les sept groupes de frise, le premier, noté p111 dans le système des cristallographes, est engendré par une translation. Le second, noté p112, est engendré par une translation et une symétrie centrale. On montre alors qu'il contient une infinité de symétries centrales, dont les centres sont équidistants. Plus précisément, la longueur de la translation est égale au double de la distance séparant deux centres de symétrie consécutifs.
La propriété remarquable de la première formule de harpe de la figure 3 est qu'elle est invariante par une symétrie centrale, c'est-à-dire que son groupe de symétrie est de type p112 (et non pas seulement p111). Pour placer le centre de symétrie en début de formule, décalons celle-ci de deux couples vers la droite (voir la figure 11). On remplace la numérotation des couples précédente, par une numérotation des cordes elles-mêmes, indiquée sous la figure, en notant de 0 à 4 les cordes du grave à l'aigu. Les centres de symétries sont alors matérialisés graphiquement par des petites croix. On a de plus relié par des traits les deux lignes invariantes par symétrie centrale. Ces tracés zigzagants donnent une image de la formule bien différente de celle utilisée figure 3 pour la mise en évidence du canon.
|
Figure 11: Symétries centrales
d'une formule de harpe nzakara.
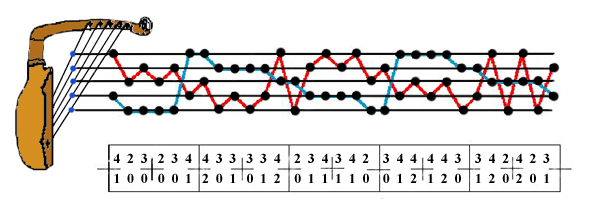 |
Pour vérifier la symétrie, on prend la première paire {1, 4} et la dernière {1, 3}. Leurs éléments peuvent être groupés par deux de telle sorte que la somme modulo 5 soit constante : 1 + 1 = 3 + 4 = 2. De même, lorsqu'on prend les autres paires, on trouve toujours la même somme constante égale à 2 quand on les associe à la paire en même position à partir de la fin.
Si la théorie des groupes de symétrie date du XIXe siècle, l’exploration des différents types de symétrie a commencé bien avant, dans les productions artistiques des civilisations non occidentales, et particulièrement dans leurs figures ornementales. L'utilisation des 17 types de symétrie plane est déjà manifeste dans les décorations de l’architecture arabe (mosaïque, carrelage). Il est généralement admis que la variété de symétries obtenues par les artistes arabes n'est pas le fruit du hasard, mais plutôt le résultat d'une recherche systématique ayant pour but d'obtenir la diversité la plus grande possible. Dans la musique également (mais cette fois, il s'agit de la musique occidentale), l'utilisation de la rétrogradation et de l'inversion est attestée depuis les temps les plus reculés. La question est donc posée de savoir si l'apparition de propriétés de ce type dans un répertoire musical de tradition orale s'inscrit dans le même processus cognitif.
Malheureusement, cette propriété de symétrie n'est pas vraie pour toutes les formules de harpe en canon du répertoire nzakara. On peut vérifier en effet que la deuxième formule de la figure 3 n'a pas de symétrie centrale. Dans ces conditions, l'argument combinatoire évoqué plus haut ne plaide pas en faveur d'une explication d'ordre cognitif à l'apparition de symétries centrales dans les fomules de harpe nzakara. D'un côté, il est remarquable qu'une formule admette ce type de symétrie, mais de l'autre, elle apparaît comme un cas particulier isolé, qui ne s'inscrit pas dans un processus mental d'exploration systématique.
Bibliographie
AROM
S., Polyphonies et
polyrythmies d'Afrique centrale. Structure et
méthodologie, Paris, Selaf, 1985.
AROM Simha, BAHUCHET Serge, EPELBOIN Alain, FÜRNISS Susanne, GUILLAUME Henri, THOMAS Jacqueline M.C.,« Pygmées Aka. Peuple et musique », CD ROM, Montparnasse multimedia, CNRS Audiovisuel, ORSTOM, 1998.
BOUCHET, A., « Imparité rythmique », CultureMATH, 2010
BRENNER, Klaus-Peter, Die kombinatorisch strukturierten Harfen-und Xylophonpattern der Nzakara (Zentralafrikanische Republik) als klingende Geometrie – eine Alternative zu Marc Chemilliers Kanonhypothese, Bonn: Holos-Verlag, 2004.
BRENNER, Klaus-Peter, « Audio Recordings – another Case Study: Restudying and Re-restudying Historical Recordings of Nzakara Harp Songs », 39th World Conference of the ICTM, Vienna, Austria, 4-11 July, 2007
DAMPIERRE É. de, Une esthétique perdue, Paris, Presses de l'Ecole Normale Supérieure, 1995.
CHEMILLIER M., « Représentations musicales et représentations mathématiques », L'Homme, numéro spécial « Musique et anthropologie », 171-172, 2004, p. 267-284.
CHEMILLIER M., « Synchronization of musical words », Theoretical Computer Science 310 (2004), p.35-60.
CHEMILLIER M., « Mathématiques de tradition orale », Math. Sci. hum., n° 178, 2007 (2), p.11-40.
CHEMILLIER, Marc & TRUCHET, Charlotte, « Computation of words satisfying the “rhythmic oddity property” (after Simha Arom’s works) », Information Processing Letters 86 (2003), p. 255-261.
CHEMILLIER M., Les Mathématiques naturelles, Odile Jacob, 2007
« Mathématiques exotiques », Dossier spécial de Pour la Science, avril-juin 2005
AROM Simha, BAHUCHET Serge, EPELBOIN Alain, FÜRNISS Susanne, GUILLAUME Henri, THOMAS Jacqueline M.C.,« Pygmées Aka. Peuple et musique », CD ROM, Montparnasse multimedia, CNRS Audiovisuel, ORSTOM, 1998.
BOUCHET, A., « Imparité rythmique », CultureMATH, 2010
BRENNER, Klaus-Peter, Die kombinatorisch strukturierten Harfen-und Xylophonpattern der Nzakara (Zentralafrikanische Republik) als klingende Geometrie – eine Alternative zu Marc Chemilliers Kanonhypothese, Bonn: Holos-Verlag, 2004.
BRENNER, Klaus-Peter, « Audio Recordings – another Case Study: Restudying and Re-restudying Historical Recordings of Nzakara Harp Songs », 39th World Conference of the ICTM, Vienna, Austria, 4-11 July, 2007
DAMPIERRE É. de, Une esthétique perdue, Paris, Presses de l'Ecole Normale Supérieure, 1995.
CHEMILLIER M., « Représentations musicales et représentations mathématiques », L'Homme, numéro spécial « Musique et anthropologie », 171-172, 2004, p. 267-284.
CHEMILLIER M., « Synchronization of musical words », Theoretical Computer Science 310 (2004), p.35-60.
CHEMILLIER M., « Mathématiques de tradition orale », Math. Sci. hum., n° 178, 2007 (2), p.11-40.
CHEMILLIER, Marc & TRUCHET, Charlotte, « Computation of words satisfying the “rhythmic oddity property” (after Simha Arom’s works) », Information Processing Letters 86 (2003), p. 255-261.
CHEMILLIER M., Les Mathématiques naturelles, Odile Jacob, 2007
« Mathématiques exotiques », Dossier spécial de Pour la Science, avril-juin 2005
Liens
AROM, Simha, Le CD-ROM Pygmées Aka, peuple et musique, Musimediane, n° 3, mai 2008. Interview menée par Marc Chemillier.
« Modèles mathématiques pour l'informatique musicale: outils théoriques et stratégies pédagogiques », par Marc Chemillier et Moreno Andreatta
Page web de Marc Chemillier