CultureMATH - accueil - contact

Sommaire

Introduction : commentaires - diaporama

• 1 Le diaporama
• 2 Trois niveaux de réflexion
• 3 Le choix de la géométrie
• 4 Mais d’abord, qu’est ce que la géométrie ?
• 5 Renouveau

Première partie:
l’élaboration de la géométrie comme science mathématique - commentaires - diaporama

• 6 En Egypte : un extrait du papyrus Rhind
• 7 Scruter la nature
• 8 – 9 Problèmes de pyramides
• 10 En Mésopotamie : le problème des six frères
• 11 La diagonale du carré
• 12 – 14 Du particulier à l’universel
• 15 – 16 Encore une autre culture : les mathématiques chinoises
• 17 – 19 Diversions et Digressions
• 20 Une étape décisive vers la constitution de l’idéalité mathématique : la découverte de l’incommensurabilité
• 21 La soustraction réciproque
• 22 Grandeurs incommensurables (1)
• 23 Grandeurs incommensurables (2)
• 24 L’algorithme d’Euclide par Euclide
• 25 La théorie des proportions
• 26 Élaboration d’objets idéaux
• 27 Vers une théorie mathématique
• 28 Cette théorie commence par des définitions
• 29 Et les démonstrations s’organisent en théorèmes lesquels s’appuient sur des notions communes (qu’aujourd’hui on appelle plutôt axiomes)
• 30 Un exemple célèbre : le théorème de Pythagore (I, 47)
• 31 L’organisation des Éléments illustrée par l’exemple du théorème de Pythagore
• 32 – 35 En résumé
• 36 La théorie de la connaissance chez Platon
• 37 La géométrie pour Platon
• 38 Conclusion de la première partie

Seconde partie:
vers les géométries non euclidiennes et une autre conception de la géométrie - commentaires - diaporama

• 39 Un grain de sable : le postulat des parallèles
• 40 Demandes ou postulats
• 41 Le postulat des parallèles
• 42 – 43 Intermède : où était l’erreur ?
• 44 La critique de Proclus (412 – 485)
• 45 La géométrie absolue
• 46 La position stratégique de la proposition 29
• 47 Prouver le postulat des parallèles
• 48 Propriétés équivalentes au postulat des parallèles
• 49 – 50 La démonstration de Wallis
• 51 – 52 Le point d’achoppement : qu’est-ce qu’une droite ?
• 53 Le scandale de la géométrie
• 54 Peut-on développer une géométrie déductive sans le [PP] ?
• 55 La Géométrie absolue
• 56 Comment alors se représenter une telle géométrie ?
• 57 Droites et cercles dans le modèle de Poincaré
• 58 – 59 Les parallèles de Lobatchevskij en géométrie hyperbolique
• 60 – 61 Cercle circonscrit à un triangle
• 62 Un carré en géométrie hyperbolique
• 63 – 65 Quadrature du cercle
• 66 La quadrature du cercle en géométrie hyperbolique
• 67 – 68 Carrés en perspective
• 69 – 70 Escher
• 71 Comparons les deux types de développement : celui de la géométrie euclidienne et celui de la géométrie non euclidienne
• 72 Les définitions
• 73 Les axiomes
• 74 Statut de la vérité en mathématiques
• 75 Conséquences épistémologiques
• 76 Problème logique : comment deux théories, basées sur deux propositions contradictoires, peuvent-elles coexister ?
• 77 Un autre exemple : les nombres complexes
• 78 Deux logiques mathématiques différentes
• 79 Conclusion en forme de question : la déraisonnable aptitude des mathématiques à expliquer la nature

Introduction

1 Le diaporama

Le diaporama qui suit a été élaboré en Terminale scientifique à la demande conjointe d’Élisabeth ARBOGAST, professeur de mathématiques et Nafissa HAIDAR, professeur de philosophie, toutes deux au lycée Ribeaupierre de Ribeauvillé (Haut-Rhin). Au départ, Mme Haidar avait souhaité un exposé sur la géométrie non euclidienne et à partir de là, aborder les questions d’épistémologie au programme de la classe de Terminale Scientifique. Très vite, nous nous sommes mis d’accord sur l’objectif suivant : mettre en mouvement une dynamique de réflexion qui rompe avec le cloisonnement disciplinaire, et qui amène les élèves à se dire lorsqu’ils font des mathématiques : quel est le sens de ce que je fais en mathématiques ? En quoi est-ce une science exacte ? Comment s’est–elle construite ? Quel lien avec ce que je fais en philosophie ? Etc. Et lorsqu’ils sont en cours de philosophie : quels exemples puis-je tirer de mes autres apprentissages, mathématiques, physique, SVT, etc. pour donner corps aux concepts philosophiques, pour illustrer des thèmes comme intuition, évidence, vérité, rigueur, imagination, réalité, etc. ? D’où :

2 Trois niveaux de réflexion

- Historique : comment naît et se construit une théorie mathématique ?

- Épistémologique : quelles connaissances nous donne l’histoire de cette construction sur le fondement et la validité des théories mathématiques, sur la vérité de leurs jugements ?

- Philosophique : quel est le statut de la vérité en mathématiques et le rôle de la démonstration dans ce statut ? Que nous disent les mathématiques sur le réel ?

3 Le choix de la géométrie

Bien qu’aujourd’hui cette discipline mathématique ne soit plus la partie dominante des programmes de l’enseignement au lycée, la géométrie s’imposait néanmoins dans cette réflexion interdisciplinaire pour au moins quatre raisons :

- La géométrie est à la fois la plus ancienne et la plus moderne des théories mathématiques. C’est par elle que se sont posées les questions d’universalité des vérités mathématiques, c’est par elle que s’est élaboré l’idée de démonstration.

- La géométrie a longtemps représenté le modèle de la rigueur mathématique au point que durant toute la période classique (17^e et 18^e siècles) on ne disait pas ‘’mathématicien’’ mais ‘’géomètre’’ pour qualifier le métier de mathématicien.

- La géométrie est celle des disciplines mathématiques qui a eu l’histoire la plus mouvementée, (d’où le qualificatif de théorie la plus moderne, évoqué au §1), ayant été l’objet d’une transformation complète au 19^e siècle et s’étant ramifiée en une multitude de sous-théories différentes : géométrie euclidienne ou non euclidienne, hyperbolique, elliptique ou riemannienne, géométrie affine, projective, analytique, synthétique, différentielle, etc.

- Enfin, c’est la géométrie qui pose le mieux la question du rapport entre les mathématiques et la réalité, car elle traite de l’espace et donc établit un lien immédiat entre une réalité au départ physique et l’abstraction mathématique qui tente d’appréhender, codifier, décrire et agir (sur) cet espace.

4 Mais d’abord, qu’est ce que la géométrie ?

En voici une définition plutôt ancienne, extraite de la grande Encyclopédie de Diderot-D’Alembert :

La géométrie est la science des propriétés de l’étendue (…). Ce mot est formé de deux mots grecs, γε ou γαία, terre, et μετρία, mesure ; et cette étymologie semble nous indiquer ce qui a donné naissance à la géométrie : imparfaite et obscure dans son origine comme toutes les autres sciences, elle a commencé par une espèce de tâtonnement, par des mesures et des opérations grossières, et s’est élevée peu à peu à ce degré d’exactitude et de sublimité où nous la voyons.

Cette définition met l’accent sur la mesure et, effectivement, l’arpentage a été longtemps et est encore le travail spécifique du géomètre professionnel. Elle décrit bien la conception que l’on avait de la géométrie jusqu’au 19^e siècle, Legendre ouvre encore la 11^e édition des ses Éléments de Géométrie (1817) par cette phrase : La Géométrie est une science qui a pour objet la mesure de l’étendue.

5 Renouveau

Or en quelques décennies cette conception va changer radicalement et sera totalement bouleversée, principalement par les travaux de deux jeunes mathématiciens auxquels je voudrais dédier cette présentation :

Lobatchevskij Nicolaï Ivanovitch (1792 – 1856)

est né à Nijni-Novgorod (Russie) en 1792. Fils d'un paysan, il fut élevé à Kazan où dès 1811 il donnait des répétitions de mathématiques. Professeur adjoint à l'université en 1814, il devint titulaire en 1816 et occupa la chaire de mathématiques pendant quarante ans, tout en faisant parfois des cours de physique et d'astronomie. Pendant dix-neuf ans, il fut recteur de l'université. Dès 1814 il s’est intéressé au problème des parallèles, et à la possibilité de développer une géométrie basée sur la négation du V e postulat d’Euclide (celui qui, dans sa forme moderne énonce que par un point pris hors d’une droite on peut mener une et une seule parallèle à cette droite). D’où de nombreuses publications sur ce thème, en russe, en français (sous le titre Géométrie imaginaire - 1837) et surtout en allemand ( par ex. GeometrischeUntersuchungen zur Theorie der Parallelinien- Berlin, 1840). La traduction en français par Hoüel de ce dernier ouvrage en 1866 fit connaître et peu à peu accepter ses idées dans la communauté mathématique.

Bólyai János (1802 – 1860)

est né à Cluj (Roumanie) en 1802. Son père Farkas, (1775, 1856) est lui-même resté un mathématicien célèbre par son ouvrage majeur Tentamen, et surtout par une longue et importante correspondance avec Gauss avec qui il s’était lié d’amitié à Göttingen. Tous deux s’intéressaient au problème des parallèles et Farkas montra l’équivalence du postulat des parallèles avec l’existence d’un cercle passant par trois points non alignés. Malgré la désapprobation de son père, le jeune János commença à réfléchir à ce problème et acquit rapidement la conviction que la négation du postulat des parallèles ne conduisait pas à une contradiction. En 1832 Il publia le résultat de ses découvertes dans une annexe au Tentamen sous le titre : La science absolue de l’espace indépendante de la vérité ou de la fausseté de l’axiome XI d’Euclide[1] (que l’on ne pourra jamais établir a priori) ; suivi de la quadrature géométrique du cercle, dans le cas de la fausseté de l’axiome XI. Dans cet ouvrage, János Bólyai développe surtout ce qu’il appelle la Géométrie absolue, c’est à dire l’ensemble des propositions de géométrie que l’on peut déduire des définitions et des axiomes proposés par Euclide sans avoir recours au V e postulat. Comme pour Lobatchevskij, c’est la traduction française par Hoüel, en 1868, qui fit connaître l’œuvre de János Bólyai.

Nous étudierons en détail ces questions et retrouverons ces deux mathématiciens dans la seconde partie de cet exposé. Auparavant nous allons tenter de parcourir 4000 ans d’histoire de la géométrie pour comprendre comment s’est élaborée au fil des siècles une telle théorie mathématique.

Retour au sommaire

Première partie : l’élaboration de la géométrie comme science mathématique.

6 En Egypte : un extrait du papyrus Rhind

Le papyrus Rhind, du nom de l’Écossais Henry Rhind qui l’acheta en 1858 à Louxor. Actuellement conservé au British Museum (Londres), c’est un des plus vieux textes mathématiques, ayant aujourd’hui près de 4000 ans. Il est actuellement conservé à Londres au British Museum et est écrit en cursive hiératique, comme on peut le voir ci contre, mais il existe des versions en hiéroglyphes telles que celle de la diapositive suivante.

7 Scruter la nature

L’introduction au document se propose un programme fort ambitieux :

Exemples de calcul pour scruter la nature et connaître tout ce qui existe, chaque mystère, …chaque secret [2].

Même si elle peut paraître exagérée, une telle présentation manifeste une conscience déjà très forte du pouvoir des nombres et de l’art du calcul. Nous connaissons l’âge du papyrus Rhind, parce que le scribe Ahmose qui l’a écrit a mentionné la date :

L’an 33, durant le quatrième mois de la saison de l’inondation, sous la majesté du roi de haute et basse Égypte Aaoussérré, doué de vie, conformément aux écrits des temps anciens qui ont été faits au temps du roi Ny-ma-ât-Rê.

Cela montre bien que le scribe Ahmose s’appuie sur un document encore plus ancien.

8 – 9 Problèmes de pyramides

Le papyrus contient 87 problèmes avec leurs solutions. Écrit dans l’Égypte ancienne, on ne s’étonnera pas d’y trouver des problèmes sur des pyramides, tels le problème 56 : Exemple de calcul d’une pyramide dont le côté est 360 et la hauteur qui lui appartient est 250. Fais moi savoir ce que sera sa pente. Suit une série de calculs que nous n’étudierons pas ici, mais qui permet de prendre connaissance de la façon dont les Égyptiens écrivaient les nombres entiers et les fractions. Contentons nous de constater qu’ils expriment le rapport 180/250 par la somme des fractions 1/2, 1/5, 1/50, et que la diapo. N° 9 présente le calcul de la multiplication de 1/2+1/5+1/50 par 7, qui donne 5 + 1/25  pour exprimer la pente en palmes.

10 En Mésopotamie : le problème des six frères

Dans un autre contexte, celui de la civilisation babylonienne, le Problème des six frères[3] montre, outre l’existence, là aussi, d’un système de numération (sexagésimal) déjà bien élaboré, une visée pédagogique illustrée par la solution proposée. Celle-ci indique les opérations à effectuer pour y arriver, afin sans doute de servir de modèle pour d’autres problèmes semblables. Maurice Caveing, qui en a fait une étude approfondie le présente ainsi :

Cette tablette ne contient qu’un seul problème, dans lequel on demande de partager l’aire d’un trapèze en six parts, égales par paires, qu’il s’agit de déterminer au moyen de la longueur de leurs côtés. La solution est constituée par un ensemble de dix-neuf nombres entiers. Comment celui-ci a-t-il été construit ? L’analyse du texte montre que la trichotomie initiale du trapèze est rattachée à un calcul arbitraire, que le calculateur a probablement recherché sans y parvenir, la plus petite solution, et que les « triplets pythagoriques » y jouent un rôle essentiel. On possède ainsi un témoignage instructif sur les ambitions et les limites de la « mathématique » babylonienne.

On peut cependant être impressionné par les connaissances mises en jeu, impliquant entre autres une parfaite maîtrise de ce que l’on appelle la moyenne quadratique de deux nombres (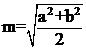) correspondant au segment parallèle à la base et qui partage un trapèze en deux parties de même aire.

11 La diagonale du carré

Une autre tablette présente le calcul de la diagonale d’un carré de côté 30, obtenu par la multiplication de ce côté par 1, 24, 51, 10 en numérotation sexagésimale, soit

 

c'est-à-dire 1,414213, en écriture décimale. Le résultat est écrit en dessous de la diagonale : 42, 25, 35, soit 42, 4264.

Comme dans la tablette précédente, le calcul se fait uniquement sur un exemple numérique précis, mais laisse supposer une compréhension universelle de la situation, à savoir que quelle que soit la dimension du carré, la relation entre le côté et la diagonale est toujours la même. Ce renvoi à l’universel est d’autant plus flagrant qu’il s’appuie sur le calcul approché d’un rapport que les Grecs qualifierons d’irrationnel et qui ne peut pas s’exprimer de façon exacte avec un nombre fini de symboles. Jusqu’où allait la conscience de cette impossibilité, nous n’en avons aucune idée.

Retour au sommaire

12 – 14 Du particulier à l’universel

En tout cas est ainsi posée la question fondamentale de l’universalité de certaines propriétés des figures géométriques, universalité qui a dû s’imposer progressivement à l’esprit de certains arpenteurs et que l’on peut considérer comme un premier pas vers l’idée de preuve. La constatation empirique que la somme des angles d’un triangle est constante et égale à un angle plat, par exemple, a dû soulever la question d’une validation de ce résultat, validation obtenue par la mise en œuvre d’une argumentation visuelle aboutissant à l’énoncé d’une propriété définitivement admise après cette validation.

15 – 16 Encore une autre culture : les mathématiques chinoises

Ce type de validations n’est pas explicité dans les papyrus égyptiens ou dans les tablettes babyloniennes, mais elles se rencontrent dans des documents chinois très anciens, telle cette « figure de l’hypoténuse qui « démontre » une relation générale entre les côtés d’un triangle rectangle. Ce n’est pas le théorème de Pythagore mais une relation voisine qui pourrait y conduire. La figure proposée dans le texte chinois est particulière (pour un triangle 3, 4, 5 ; mais le raisonnement est valable pour tous les triangles rectangles. La démonstration du théorème de Pythagore se trouve, elle dans un texte plus récent, qui est en fait un commentaire d’un texte plus ancien : les neuf chapitres sur l’art du calcul, par Liu Hui, vers 270 avant J.C.

17 – 19 Diversions et Digressions

On peut légitimement s’interroger sur la validité de ce type de preuve. Pour en marquer le caractère discutable, faisons un saut dans le temps pour nous rapprocher de notre époque et posons une petite énigme géométrique inventée par le célèbre logicien Lewis Carroll (1832 – 1898), bien connu pour son Alice au pays des merveilles. Un carré 8x8 (l’unité n’a pas d’importance) est découpé comme le montre la figure en deux trapèzes rectangles (de bases 5 et 3, de hauteur 5) et en deux triangles rectangles (côtés de l’angle droit : 8 et 3). Le carré 8x8 est maintenant découpé selon ces quatre morceaux lesquels sont réajustés exactement pour former un rectangle de dimensions 5x13. Problème : le rectangle 8x13 a une aire de 65 alors que le carré initial avait une aire de 64. D’où vient le carré unité supplémentaire ? Nous ne donnons pas pour l’instant la solution de l’énigme ; l’ensemble des trois diapositives peut faire l’objet d’une petite pose ludique. La réponse sera donnée un peu plus loin.

Retour au sommaire

20 Une étape décisive vers la constitution de l’idéalité mathématique : la découverte de l’incommensurabilité

Revenons à la tablette babylonienne montrant le calcul de la diagonale d’un carré. Outre la question de l’universalité, nous avions évoqué le problème de l’irrationalité du rapport entre le côté et la diagonale d’un carré. Comment et quand ce caractère irrationnel a-t-il été découvert et démontré ? Nous n’avons pas de réponse précise à ces questions, mais l’histoire des mathématiques grecques a laissé la trace d’un épisode traumatisant (d’où le terme d’irrationnel qui manifeste l’irruption de quelque chose d’impensable, de déconcertant) pour les Pythagoriciens qui avaient construit toute une conception du monde et de son appréhension par une science basée sur les nombres (entiers) et le rapport de nombres.

(N.B. Ici sont développés quelques aspects techniques que le lecteur peut sauter pour aller directement à la diapo.24)

21 La soustraction réciproque

Ainsi, soit par exemple à comparer les longueurs des deux segments AB = a et CD = b. Les mathématiciens grecs utilisaient un algorithme qu’ils appelaient ‘’ soustraction réciproque’’ que l’on peut décrire ainsi. Plaçons les deux segments perpendiculairement de façon à ce qu’ils forment un rectangle de côtés a et b (a > b) et construisons le maximum de carrés contigus de côté b inscrits dans ce rectangle. Dans l’exemple proposé il y en a deux et il reste un petit rectangle de côtés b et a₁ < b. Donc a = 2b + a₁. Recommençons la même opération dans ce petit rectangle : on arrive à b = 3a₁ + a₂. Continuons encore ; on a : a₁ = 2a₂. Ici le processus s’arrête et on peut en déduire, en remontant que b = 7 a₂ et a = 16a₂. de sorte que l’on peut carreler complètement le rectangle axb avec des petits carrés de côté a₂ au nombre de 16x7. Mais surtout a et b sont multiples d’une même longueur a₂ qui est une mesure commune aux deux longueurs et qui permet de dire que a est à b sont comme 16 à 7. On dit aussi que les segments AB et CD sont commensurables. Certains d’entre vous reconnaîtront dans le processus de la ‘’soustraction réciproque ce qu’ils connaissent sous l’expression « algorithme d’Euclide » Il y a cependant une différence : l’algorithme d’Euclide concerne uniquement des nombres entiers, alors que la ‘’soustraction réciproque’’ peut s’appliquer à des grandeurs quelconques, ce qui pose le problème suivant :

22 Grandeurs incommensurables (1)

Le processus de la ‘’soustraction réciproque’’ s’arrête-t-il nécessairement au bout d’un nombre fini d’étapes comme ci-dessus et comme c’est le cas pour l’algorithme d’Euclide ?

Considérons un rectangle ABCD et E le milieu de [AB]. Construisons le rectangle ADGF en reportant la longueur ED sur le côté [BA] prolongé et en complétant les autres sommets. Alors les deux rectangles BCGF et ADGF sont semblables, dans le sens que les rapports de leurs côtés sont égaux. On pourrait démontrer cela à la manière d’Euclide mais cela suppose la mise en place d’un certain nombre de propositions intermédiaires. Le lecteur sera plus familier avec un calcul de longueur.

Si l’on note AB = a et BC = b, alors :

ED =

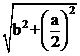xBF =

+

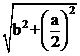et xxxxxxAF =

-

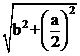On vérifie alors facilement que

BF / BC = BC / AF

ou que

BC² = BF x AF

Mais dans ce cas, le processus de la 'soustraction réciproque' ne se terminera jamais, comme on peut le comprendre sur l’exemple de la figure de droite dans lequel a = 4b. Quelle que soit l’étape envisagée, il restera toujours un rectangle semblable au précédent et l’opération n’aboutira jamais. Les deux côtés BF et BC sont incommensurables ; leur rapport est irrationnel, égal à .

23 Grandeurs incommensurables (2)

De même nous pouvons mettre en évidence l’incommensurabilité de la diagonale d’un carré avec son côté. Considérons le carré ABCD de côté a et le rectangle EDCF de côtés DC = a et DE = d, diagonale du carré ABCD. Une fois qu’on a enlevé le carré ABCD du rectangle EDCF, il reste un rectangle ABFE de côtés AB = a et AE = d – a. A cause de d² = 2a² il est facile de vérifier que

2(d – a) < a < 3(d – a),

donc on peut enlever deux carrés de côté (d – a) dans le rectangle ABFE, et il reste un rectangle GBFH, de côtés BF = d – a et GB = a – 2(d – a) = 3a – 2d.

Mais comme d² = 2a² qui peut aussi s’écrire :

_,

on en déduit que les rectangles ABFE et GBFH sont semblables, donc que l’on peut à nouveau enlever deux carrés au rectangle GBFH, laissant un nouveau petit rectangle semblable aux précédents, etc. Le processus de ‘’soustraction réciproque’’ ne s’arrêtera jamais ; la diagonale est incommensurable au côté du carré et leur rapport est irrationnel.

24 L’algorithme d’Euclide par Euclide

La découverte de l’existence de grandeurs incommensurables a certainement contribué fortement à repenser les bases de la géométrie, puisque cela signifiait que certaines grandeurs n’étaient pas mesurables exactement. On en trouve trace dans les Éléments_[4] d’Euclide (et c’est ce qui explique l’algorithme du même nom), mais sous les deux formes :

1) pour des nombres entiers

2) pour deux grandeurs inégales quelconques, définissant ainsi la notions de grandeurs incommensurables.

Lorsque les grandeurs sont commensurables, il existe une mesure commune qui permet d’exprimer leur rapport au moyen d’un quotient de deux nombres entiers, tel l’exemple de la diapo. N° 21. Mais lorsque les grandeurs sont incommensurables ? Faudra-t-il se priver de toute comparaison ? Le livre V des Éléments d’Euclide traite de ce problème en élaborant une théorie des proportions pour toutes les situations : aussi bien celles où les grandeurs sont commensurables (on parlera de rapport rationnel) que celles où elles sont incommensurables (on parlera de rapport irrationnel).

Retour au sommaire

25 La théorie des proportions

Dans la figure présentée ici, je ne peux pas exprimer par un nombre (ou un rapport de nombres entiers) la relation entre, par exemple, les longueurs AB et OB, ou la longueur de la circonférence (ABCD) et le côté du carré qui lui est inscrit. Mais les Éléments d’Euclide, et particulièrement le Livre V permettent :

1) de dire que les aires des deux carrés sont dans un rapport de 1 à 2 (cela est déjà possible avec le Livre I)

2) de démontrer que le rapport des aires des deux cercles est aussi de 1 à 2 (Livre XII)

3) de démontrer que

ou que

 

(ici, il s’agit uniquement de comparer des rapports, sans que cette fois ci on puisse faire référence à un nombre - c’est pour cela que ces rapports sont qualifiés d’irrationnels),

4) plus généralement, de démontrer des propriétés universelles sur le rapport de l’aire d’un cercle à celle du carré inscrit, ou sur le rapport de la circonférence d’un cercle à la longueur de son diamètre.

26 Élaboration d’objets idéaux

L’incommensurabilité, les raisonnements et les algorithmes qui la mettent en évidence obligent à penser la droite comme un objet abstrait qu’on ne peut plus confondre avec ses modèles physiques : trait graphique, arête d’un mur, faîte d’un toit, etc. Tant que l’on travaille avec de tels modèles, la géométrie relève plutôt de l’arpentage et reste un art expérimental où aucun processus infini ne peut avoir lieu. Cet objet abstrait doit se soumettre à d’autres règles que celles fournies par la mesure : celles imposées par les définitions et les propriétés déduites par raisonnement. C’est là que commence vraiment la géométrie.

Retour au sommaire

27 Vers une théorie mathématique

Au total :

- l’exigence de certitude conduit à élaborer des processus d’argumentation, des démonstrations

- la découverte de grandeurs incommensurables oblige à dépasser la considération d’objets sensibles au profit d’objets pensés et abstraits

- l’aspect arpentage et mesure cède le pas à l’aspect conceptuel et déductif.

- l’outil de base est le rapport et la proportion qui permet la comparaison de tous les objets géométriques, qu’ils soient commensurables ou non.

On sait, par différents témoignages qu’il y a eu plusieurs tentatives de mise en forme de ces exigences, la plus aboutie qui va remplacer toutes les autres étant celle d’Euclide (environ 300 av. J.C.)

28 Cette théorie commence par des définitions

comme par exemple :

- Un point est ce dont il n’y a aucune partie.

- Une ligne droite est celle qui est placée de manière égale par rapport aux points qui sont sur elle.

- Et quand une droite, ayant été élevée sur une droite, fait les angles adjacents égaux entre eux, chacun de ces angles égaux est droit, et la droite qui a été élevée est appelée perpendiculaire à celle sur laquelle elle a été élevée.

29 Et les démonstrations s’organisent en théorèmes lesquels s’appuient sur des notions communes (qu’aujourd’hui on appelle plutôt axiomes)

- les notions communes sont considérées comme ne nécessitant aucune démonstration pour être acceptées par tout un chacun ; par exemple que les choses égales à une même chose sont égales entre elles.

- Les théorèmes (ou propositions) sont par contre des propositions démontrées, sur lesquelles de nouvelles démonstrations peuvent s’appuyer.

Retour au sommaire

30 Un exemple célèbre : le théorème de Pythagore (I, 47)

Ce théorème n’est pas appelé ainsi par Euclide qui lui donne juste un numéro. Mais il est représentatif de la démarche euclidienne, illustrée schématiquement ici en quatre étapes :

1) l’égalité du demi carré en orange avec le triangle en bleu

2) l’égalité du triangle en bleu et du triangle en vert

3) l’égalité du triangle en vert et du demi rectangle en orange

4) l’égalité du demi carré avec le demi rectangle et donc aussi du carré avec le rectangle.

En faisant un raisonnement analogue avec le carré et le rectangle de droite et en ajoutant on obtient bien le résultat connu sous l’expression « théorème de Pythagore » : le carré sur le côté sous-tendant l’angle droit est égal aux carrés sur les côtés contenant l’angle droit.

31 L’organisation des Éléments illustrée par l’exemple du théorème de Pythagore

Le vocabulaire même est évocateur si l’on revient à l’étymologie du mot grec Éléments, traduction de ΣΤΟΙΧΕΙΑ, qui signifie à l’origine et simultanément :

- plantation d’arbres

- principe d’un bon gouvernement

- acte d’avancer en rang, comme une armée en ligne de bataille, et met donc en évidence deux sens du mot « Éléments :

1) principe constituant d’une chose

2) organisation de ces principes en un tout rangé et ordonné.

L’organigramme de droite montre alors toutes les connections que l’on peut établir (et qui sont d’ailleurs mentionnées explicitement par Euclide, de proche en proche) entre les définitions, les postulats (ou demandes) les axiomes et les propositions successives, au fur et à mesure de leurs démonstrations.

Retour au sommaire

32 – 35 En résumé

La géométrie d’Euclide s’est constituée schématiquement en trois étapes :

1) Une longue pratique avec observation et accumulation des propriétés de figures géométriques, à partir de nombreuses mesures : c’est le stade de l’expérience. Celle-ci construit les intuitions et assure le lien avec la réalité, mais elle ne peut donner ni la nécessité, ni l’universalité.

2) La découverte du caractère universel de certaines propriétés et de leur liaison logique ; mise en évidence du caractère nécessaire de cette liaison, au moyen des premières démonstrations. Ces démonstrations supposent une idéalisation de certains objets empiriques sous forme d’objets géométriques abstraits tels que le point, la droite, le plan. C’est le stade de l’intuition. Celle-ci donne une connaissance directe de son objet ; elle porte avec elle son évidence et son caractère nécessaire.

3) L’intégration de la plupart des propriétés géométriques connues en un système déductif unique, le système d’Euclide, en dégageant les propriétés de base (axiomes - en nombre minimal) desquelles découlent toutes les autres par simple déduction logique. C’est le stade de la théorie.

Au total, l’axiomatisation est le résultat d’un long processus partant de l’expérience pour arriver à la théorie, en s’appuyant sur l’intuition.

36 La théorie de la connaissance chez Platon

Ainsi la géométrie chez les Grecs a contribué à façonner une certaine conception de la connaissance en général dont elle est en même temps le reflet. Le géomètre n’invente pas, il découvre et contemple des objets idéaux préexistants dans un monde des Idées. (le mot « « théorème » a la même origine sémantique que le mot « théâtre »). C’est la philosophie de Platon pour qui « la recherche et le savoir ne sont au total que réminiscence » (Ménon, 81d) Celle-ci est expliquée dans un célèbre dialogue intitulé Ménon, dans lequel Socrate fait découvrir à un serviteur n’ayant a priori aucune connaissance géométrique comment construire un carré double d’un carré donné.

Socrate : N’est-ce pas sans avoir reçu de personne aucun enseignement, mais plutôt en étant questionné, qu’il possédera des connaissances, ayant repris de son propre fond, la connaissance qu’il se donne lui-même ?

Ménon : Oui

Socrate : Or reprendre soi-même une connaissance en soi-même, n’est-ce pas se ressouvenir ?

37 La géométrie pour Platon

Dans un autre dialogue, La République (510) Platon explique ce qu’est la géométrie et sa place dans l’organisation générale de la connaissance. Celle-ci se répartit d’abord en deux grandes sections : celle du monde visible (sensible) et celle du monde intelligible. Chacune de ces deux parties est elle-même partagée en deux, la première comprenant tout ce qui est réalité illusoire, formée des reflets, des images réfléchies (par exemple par un miroir), les ombres d’une part et tous les objets naturels et concrets de l’autre ; la seconde incluant d’une part les objets de la science (en particulier la géométrie) et qui correspondent à une réalité abstraite, et d’autre part tout ce qui relève d’une réalité spirituelle. A chacune de ces parties correspond un mode de connaissance spécifique, relevant de l’opinion pour le monde visible, de la vérité pour le monde intelligible. Les figures géométriques ont ainsi un double ancrage : dans la réalité sensible : par la figure matérielle dessinée sur un support concret ; dans la réalité abstraite par la figure pensée et étudiée par la géométrie.

« en outre ils font usage de figures visibles, et sur ces figures, ils construisent des raisonnements sans avoir à l’esprit ces figures elles-mêmes, mais les figures parfaites dont celles-ci sont des images ».

38 Conclusion de la première partie

Durant 2000 ans, la représentation intuitive de l’espace s’explicite au contact de la géométrie au point que l’espace du géomètre et l’espace sensible ne semblent former que deux aspects inséparables d’une même réalité. C’est par notre intuition et les expériences sensibles que nous nous sommes construit une certaine représentation de l’espace dont l’organisation en un système déductif a donné la géométrie euclidienne.

Retour au sommaire

Seconde partie : vers les géométries non euclidiennes et une autre conception de la géométrie.

Durant des siècles la géométrie va fonctionner et se développer sur ces principes : Archimède, Apollonius, Ptolémée pour ne citer que les plus importants, vont poursuivre l’œuvre d’Euclide tout en s’appuyant entièrement sur ses principes, particulièrement dans l’étude d’autres courbes comme les coniques, les solides et l’astronomie. Un élément, pourtant posait problème.

39 Un grain de sable : le postulat des parallèles

Rappelons la définition des droites parallèles et celles de « postulat »

Droites parallèles (définition 23 chez Euclide) : 

« sont celles qui étant dans un même plan et indéfiniment prolongées de part et d’autre ne se rencontrent pas, ni d’un côté, ni de l’autre »

40 Demandes ou postulats

Outre les définitions et les axiomes ou notions communes, Euclide a aussi posé un certain nombre de « Demandes » ou Postulats, tels que

1) Mener une ligne droite de tout point à tout point.

2) Prolonger continûment en ligne droite une ligne droite limitée.

3) Décrire un cercle à partir de tout centre et au moyen de tout intervalle.

4) Et que tous les angles droits soient égaux entre eux

Proclus, dans ses Commentaires sur le premier livre des Éléments d’Euclide (V^e siècle) explique ainsi la différence entre Postulats et axiomes :

Nous admettons dans les axiomes telles choses évidentes d’elles-mêmes pour la connaissance et à la portée de nos intelligences non enseignées ; tandis que dans les postulats, nous demandons d’admettre telles choses faciles à procurer, sur l’admission desquelles l’esprit n’est pas en peine et qui n’ont besoin ni d’artifice ni de construction.

Cela est effectivement le cas pour les quatre postulats ci-dessus, mais a l’air moins évident pour le cinquième qui concerne les parallèles et que nous désignerons par l’abréviation [PP]:

41 Le postulat des parallèles

5) [PP] : et que si une droite tombant sur deux droites fait les angles intérieurs et du même côté plus petits que deux droits, les deux droites, indéfiniment prolongées, se rencontrent du côté où sont les angles plus petits que deux droits.

Retour au sommaire

42 – 43 Intermède : où était l’erreur ?

On a une belle illustration de cette propriété dans l’explication du paradoxe soulevé dans les diapositives 17 à 19.

44 La critique de Proclus (412 – 485)

Proclus, fort de la distinction entre axiomes et postulats faite ci-dessus, considère que la propriété énoncée par le postulat des parallèles mériterait une démonstration:

« le fait que des lignes droites se rencontrent finalement lorsqu’elles s’inclinent de plus en plus l’une sur l’autre dans leur prolongement est probable et non inéluctable, à moins qu’un raisonnement ne démontre que le fait est vrai pour des lignes droites. En effet certaines lignes, indéfiniment inclinées l’une sur l’autre, sont asymptotes (…) ; dès lors ce qui est possible pour ces dernières ne l’est-il pas aussi pour les lignes droites ?»

Effectivement, pourquoi cette propriété est-elle mise au rang d’un postulat au lieu d’être démontrée ?

45 La géométrie absolue

Si l’on veut démontrer le postulat des parallèles il faut évidemment uniquement s’appuyer sur les propositions déjà démontrées qui ne le mettent pas en jeu : ce sont les 28 premières propositions des Éléments qui constituent, avec les définitions, axiomes et les autres postulats ce que Bolyai appellera la géométrie absolue, et dont on voit comment le [PP] s’introduit dans l’enchaînement déductif esquissé dans le schéma de gauche.

46 La position stratégique de la proposition 29

Les propositions 27 et 28 du Livre I énoncent respectivement que :

27. Si une droite tombant sur deux droites, fait des angles alternes égaux entre eux, ces droites seront parallèles l’une à l’autre.

28. Si une droite tombant sur deux droites, fait l’angle extérieur égal à l’angle intérieur et opposé du même côté, ou les angles intérieurs et du même côté égaux à deux droits, les droites seront parallèles l’une à l’autre. Jusque là on n’a pas eu besoin du [PP].

C’est pour démontrer la réciproque de ces deux théorèmes qu’Euclide va l’utiliser dans la proposition 29 :

29. Une ligne droite tombant sur des droites parallèles fait des angles alternes égaux entre eux et aussi l’angle extérieur égal à l’angle intérieur et opposé, et les angles intérieurs et du même côté égaux à deux droits.

Retour au sommaire

47 Prouver le postulat des parallèles

Durant vingt siècles, une multitude de mathématiciens ont tenté de démontrer le postulat des parallèles, d’abord en s’appuyant uniquement sur la géométrie absolue, puis, plus tard en essayant de montrer que la négation du [PP] conduirait à une contradiction. Nous ne pouvons retracer ici ces recherches souvent très subtiles. Le lecteur intéressé par ce problème trouvera tous les renseignements et les étapes souhaitées dans « L’aventure des parallèles »[5] ou dans « Non Euclidian Geometry »[6]

Ce que nous pouvons en retenir, c’est que toutes les soit disant ‘’démonstrations’’ se sont appuyées tôt ou tard sur une autre propriété qui pouvait paraître évidente, plus évidente que le [PP], mais dont l’admission implicite ou explicite équivalait à admettre le [PP]. Voici un échantillon de telles propriétés et leur auteur:

48 Propriétés équivalentes au postulat des parallèles

- Étant donnée une figure, il existe une figure semblable de taille arbitraire : Wallis, (1616-1703).

- Étant donnés trois points non alignés, il existe un cercle passant par ces trois points : Legendre (1752 –1833) ; Bolyai.

- Si dans un quadrilatère trois angles sont des angles droits, le quatrième aussi est un angle droit : Clairaut (1713 -1763).

- On peut construire un triangle ayant une aire donnée, arbitrairement grande : Gauss (1777-1855).

Nous en retrouverons certaines dans la suite, mais pour bien comprendre le sens de cette équivalence, détaillons en une, celle de Wallis. Outre le fait qu’elle paraît vraiment aller de soi, elle est peut-être aussi celle qui caractérise le mieux la géométrie d’Euclide en ce que celle-ci est basée sur la similitude par la théorie des proportions.

Retour au sommaire

49 – 50 La démonstration de Wallis

Soient a et b deux droites coupant une droite c en des points A et B, et faisant avec c des angles α et β tels que α + β soit inférieure à 2 droits.

Par A construisons la droite b’ faisant avec c un angle correspondant égal à β. Il est clair que b’ sera située dans l’angle adjacent à α. Déplaçons la droite b continûment le long du segment [BA] de telle façon que l’angle qu’elle fait avec c reste constamment égal à β. Avant que cette droite n’atteigne sa position finale b’, elle doit nécessairement couper a en un point C₁, déterminant ainsi un triangle AB₁C₁, avec des angles en A et en B respectivement égaux à α et β.

Selon l’hypothèse de Wallis, nous pouvons construire sur AB un triangle ABC semblable au triangle AB₁C₁. Ce qui est une manière de démontrer le postulat des parallèles, en démontrant que les droites a et b se coupent en un point C lorsqu’elles font avec une droite c des angles α et β tels que α + β soit inférieure à 2 droits.

51 – 52 Le point d’achoppement : qu’est-ce qu’une droite ?

Deux définitions :

Euclide : Une ligne est une longueur sans largeur. Une ligne droite est celle qui est placée de manière égale par rapport aux points qui sont sur elle.

En fait Euclide n’a jamais utilisé cette définition dans tout l’ensemble de ses Éléments

Legendre (1752 – 1833) : la ligne droite est le plus court chemin d’un point à un autre.

Mais on voit bien que cette définition ne convient pas non plus si on ne précise pas davantage dans quel cadre on l’utilise (diapo. 52).

Retour au sommaire

53 Le scandale de la géométrie

Dans ses Éléments de Philosophie, D'Alembert écrit à propos de la démonstration du postulat des parallèles

"On parviendrait plus facilement à la trouver, si on avait une bonne définition de la ligne droite ; par malheur cette définition nous manque"[7]

C'est cette non-définition de la droite qui conduit au scandale de la géométrie comme l'explique d'Alembert:

"La définition et les propriétés de la ligne droite, ainsi que des lignes parallèles, sont donc l'écueil et le scandale des éléments de Géométrie"[8]

Legendre fera une remarque analogue dans son mémoire de 1833 :

"C'est sans doute à l'imperfection du langage vulgaire et à la difficulté de donner une bonne définition de la droite, qu'il faut attribuer le peu de succès qu'ont obtenu les géomètres, lorsqu'ils ont voulu déduire ce théorème des seules notions sur l'égalité des triangles que contient le premier livre des Éléments."[9]

Une lecture approfondie des démonstrations du [PP] montre bien que c’est dans cette absence de définition que se situe le point d’achoppement. De quoi parle-t-on précisément lorsque l’on parle d’une droite ? S’appuyer sur le [PP] tel qu’il est énoncé chez Euclide contribue finalement et de fait à définir la droite.

D’où une autre voie d’investigation :

54 Peut-on développer une géométrie déductive sans le [PP] ?

C’est ce que fait Lobatchevskij, en s’interrogeant sur la distribution des droites passant par un point donné, en relation avec une autre droite. Ces droites seront réparties en deux groupes : celles qui coupent la droite (BC) et celles qui ne la coupent pas. Ces deux groupes seront séparés par une droite limite appelée parallèle à (BC) et cette parallèle sera caractérisée par l’angle qu’elle fait avec la perpendiculaire à (BC) appelé angle de parallélisme. Cet angle de parallélisme est une fonction décroissante de la distance de A à la droite (BC).

Retour au sommaire

55 La Géométrie absolue

Bolyai développe la Géométrie absolue en allant jusqu’au bout de ce qu’on peut construire après la proposition 28, sans adopter le [PP] , et aboutissant alors à des propriétés inhabituelles et quelquefois contradictoires à celles de la géométrie euclidienne, telles que :

- Par un point donné on peut construire plusieurs parallèles à cette droite.

- Les seules figures semblables sont les figures égales.

- Par trois points non alignés, il ne passe pas nécessairement un cercle.

- La somme des angles d’un triangle est strictement inférieure à deux droits.

- L’aire d’un triangle est bornée : Aire = k(π – somme des angles) (où k est une constante )

Une telle géométrie, que ce soit celle de Lobatchevskij ou celle de Bolyai s’appelle géométrie hyperbolique (le mot hyperbolique fait référence à une classification ultérieure des géométries).

56 Comment alors se représenter une telle géométrie ?

qui ne soit pas totalement contradictoire avec notre manière de voir les objets, autrement dit qui se sert des représentations habituelles de la géométrie euclidienne mais sans s’appuyer sur le [PP] ? Plusieurs modèles ont été proposés dont celui d’un grand mathématicien français Henri Poincaré (1854 – 1912).

Si on se limite à une géométrie plane, on peut le décrire en l’imaginant entièrement situé dans un grand cercle dont la circonférence représente alors l’horizon absolu des spectateurs habitant dans ce monde. Cet horizon représente les points à l’infini de ce plan. Un observateur situé dans ce cercle verra les objets de plus en plus petits au fur et à mesure que ceux –ci s’approche de la ligne d’horizon (c’est à dire qu’ils s’éloignent du centre.

57 Droites et cercles dans le modèle de Poincaré

Dans ce modèle, les lignes droites seront alors ou les diamètres (perpendiculaires à la ligne d’horizon) ou les arcs de cercles coupant à angles droits cette ligne d’horizon. Les cercles, quant à eux, seront tout à fait identiques aux cercles habituels de la géométrie euclidienne. Donnons alors quelques exemples de figures dans ce modèle.

58 – 59 Les parallèles de Lobatchevskij en géométrie hyperbolique

On visualisera mieux dans ce modèle la répartition des droites passant par un point E, proposée par Lobatchevskij (diapositive 55) avec la droite limite (en rouge) qui fait la séparation entre celles qui coupent (en jaune) et celles qui ne coupent pas (en vert) une droite donnée (AB). Cette droite limite qui sera la parallèle, rencontrera la droite (AB) à l’infini, c’est à dire sur le grand cercle horizon. Cette construction et les suivantes ont été réalisées grâce au site NonEuclid.

 

Retour au sommaire

60 – 61 Cercle circonscrit à un triangle

Comme l’a remarqué Bolyai (diapositive 55) il ne passe pas nécessairement un cercle par trois points non alignés, car les médiatrices des côtés du triangle peuvent

- soit ne pas se couper (diapo. 60) et alors il n’y a pas de cercle circonscrit,

- soit se couper en un unique point qui est alors le centre du cercle circonscrit.

62 Un carré en géométrie hyperbolique

Le carré en géométrie euclidienne est caractérisé par ses quatre côtés égaux et ses quatre angles droits. En géométrie hyperbolique, on ne peut pas tout garder : un carré est un quadrilatère ayant ses quatre côtés égaux et ses quatre angles égaux (mais ceux-ci ne peuvent pas être tous droits (à cause de l’aire limitée d’un triangle – voir diapo. 55)

63 – 65 Quadrature du cercle

La notion de quadrature est générale et s’applique à n’importe quelle figure plane. Il s’agit de construire à la règle et au compas une figure équivalente en aire à une figure plane donnée. Dans l’exemple célèbre de la lunule, il est facile de démontrer que l’aire limitée par la lunule (en vert) est exactement égale à l’aire du carré (en vert également). Euclide donne dans ses Éléments la méthode pour réaliser la quadrature de n’importe quelle figure rectiligne. (Voir la diapo. 64). Par contre, la quadrature d’un cercle s’est avérée être une construction impossible à réaliser et est devenue synonyme de problème impossible à résoudre.

66 La quadrature du cercle en géométrie hyperbolique

Par contre, pour certains carrés, la quadrature est possible dans le sens que son aire est un multiple rationnel du nombre π.

67 – 68 Carrés en perspective

Il ne faut pas trop s’étonner de voir dessiné des carrés qui n’ont pas la « forme des carrés habituels» en géométrie hyperbolique. Alors qu’on accepte très bien qu’en perspective les carrés du sol ne se dessinent pas non plus en « carrés habituels » !

69 – 70 Escher

Et des artistes comme Escher ont élaboré tout un art de représentations basées sur les règles de la géométrie hyperbolique.

Retour au sommaire

71 Comparons les deux types de développement : celui de la géométrie euclidienne et celui de la géométrie non euclidienne

D’où une autre manière de poser les bases de la géométrie moderne. Celles–ci sont données par Hilbert (1862 – 1943) dans un ouvrage célèbre intitulé « Fondements de la géométrie » publié en 1899.

72 Les définitions

- Nous pensons trois systèmes différents de choses : nous nommons les choses du premier système des points (…); nous nommons droites, les choses du deuxième système (…) ; nous appelons plans les choses du troisième système.

- Entre les points, les droites et les plans nous imaginons certaines relations que nous exprimons par des expressions telles que : être sur, entre, …La description exacte (…) de ces relations est donnée par les axiomes de la géométrie.

73 Les axiomes

- Axiomes d’appartenance : par exemple, il existe une droite liée à deux points donnés à laquelle appartiennent ces deux points ;

- Axiomes d’ordre : définissent des expressions comme : A est entre B et C ou la notion de segment ;

- Axiomes de congruence : définissent par ex. la congruence (égalité) de deux segments ;

- Axiome des parallèles ;

- Axiomes de continuité : par exemple, l’axiome d’Archimède qui dit que si j’ai deux grandeurs a et b (a < b) alors il existe un entier n tel que na > b.

Ces axiomes ne sont pas nécessairement tous pris en compte. Selon les choix effectués, on aura telle ou telle géométrie. En particulier, le choix de la forme donné à l’axiome des parallèles induira le type de géométrie, euclidienne ou non.

Retour au sommaire

74 Statut de la vérité en mathématiques

Cette autre manière de poser les bases de la géométrie repose sur une autre manière de concevoir la vérité des propositions mathématiques.

- Chez les Grecs, celle-ci est une vérité copie ; il y a adéquation de la chose et de l’entendement : la vérité dans l’esprit est le décalque d’une réalité hors de l’esprit, figures parfaites dont les figures (visibles) sont les images (Platon, voir diapo. 37)

- Pour Hilbert : la vérité est purement d’ordre logique : si les axiomes choisis arbitrairement ne se contredisent pas, dans toutes leurs conséquences, alors ils sont vrais, les objets définis par eux existent. Ce qui est pour moi critère de vérité et d’existence.

75 Conséquences épistémologiques

L’invention des géométries non euclidiennes remet en cause l’accord entre l’espace sensible et l’espace de la géométrie euclidienne ; elle oblige à s’interroger :

- sur la relation (qui n’est plus du tout évidente) entre la théorie que constitue la géométrie et le réel de l’espace sensible,

- sur le caractère de vérité de la géométrie, puisqu’il y a maintenant pluralité de géométries, toutes également vraies, et pourtant basées

- sur des propositions contradictoires, (dont l’une nie ce que les autres affirment).

76 Problème logique : comment deux théories, basées sur deux propositions contradictoires, peuvent-elles coexister ?

Le paradoxe peut s’expliquer de la manière suivante. Au départ, nous avons une théorie T basée sur un ensemble de définitions et d’axiomes E = {a₁,a₂, …,a_n}

Soit alors p une proposition non contenue dans T (c’est à dire qu’on ne peut pas déduire logiquement à partir de la théorie T), comme, par exemple le postulat d’Euclide si l’on prend comme théorie T la géométrie absolue. A partir de là, on peut construire deux nouvelles théories radicalement différentes : ou bien l’on prend un nouveau système d’axiomes E⁺ = {a₁,a₂, …,a_n,p} où l’on a ajouté la proposition p. Dans l’exemple précédent on obtient la géométrie d’Euclide. Ou bien l’on prend un autre nouveau système d’axiomes E^- ={a₁,a₂,…,a_n,non(p)} dans lequel on a ajouté la négation de la proposition p. Ces deux théories peuvent être plus ou moins bien adaptées à la description du monde physique, mais elles sont vraies toutes les deux, dans le sens défini par Hilbert, car elles ne présentent aucune contradiction en elles.

Nous pouvons schématiser cela par la figure à droite. Les n définitions et axiomes de la géométrie euclidienne sont illustrées par un polygone et la théorie T par le plan contenant ce polygone. La proposition p est représentée par un segment perpendiculaire d’un côté au plan T, la proposition non(p) par le segment opposé. On a ainsi construit deux pyramides opposées représentant les fondements des deux nouvelles théories.

Retour au sommaire

77 Un autre exemple : les nombres complexes

Dans l’enseignement secondaire, le professeur de mathématiques se trouve confronté à une difficulté logique de cet ordre au moment de l’introduction des nombres complexes. Longtemps il a dit aux élèves (et les a quelquefois sanctionnés) qu’un nombre négatif ne pouvait avoir de racine carrée. Et voilà qu’en classe terminale il dit tout d’un coup le contraire ! Nous sommes là tout à fait dans le même cas de figure : création d’une nouvelle théorie par négation d’une proposition jusque là affirmée.

78 Deux logiques mathématiques différentes

De fait, l’adoption d’un autre critère de vérité conduit naturellement à une autre manière d’exercer l’activité et l’invention mathématique :

- dans la logique traditionnelle, on déroule tout ce qui est possible dans une théorie donnée, le rôle de la logique étant de surveiller qu’il n’y apparaisse aucune contradiction. C’est une logique exhaustive : par rapport à un concept bien défini, sa tâche est d’épuiser le contenu du concept mais aussi d’empêcher l’intrusion d’un élément étranger sous forme de paradoxe,

- la nouvelle logique mathématique est, elle, une logique de création : elle construit des théories et des objets nouveaux par négation des concepts anciens. Elle cherche à briser la carapace du concept ancien pour en faire sortir quelque chose de neuf. Elle ne fonctionne pas par généralisation : la géométrie non euclidienne n’est pas une généralisation de la géométrie euclidienne.

79 Conclusion en forme de question : la déraisonnable aptitude des mathématiques à expliquer la nature

Le recours à l’intuition sensible à la base de la géométrie euclidienne garantissait une adéquation entre la chose pensée et la chose observée. Cette adéquation disparaît dans la nouvelle conception de la vérité mathématique et pose le problème du lien entre la théorie et la réalité. Qui d’autres que Einstein pouvait mieux exprimer cette préoccupation de la science moderne :

Comment se fait-il que la mathématique, (…) s’adapte d’une si admirable manière aux objets de la réalité ? À cette question il faut, à mon avis, répondre de la manière suivante : pour autant que les propositions de la mathématique se rapportent à la réalité, elles ne sont pas certaines, et pour autant qu’elles sont certaines, elles ne se rapportent pas à la réalité. » (La géométrie et l’expérience)

Retour au sommaire