approche-critique-comparee-des-nombres-azteques-et-mayas

1. Contrastes dans l'usage des grands nombres dans l'antiquité mésoaméricaine

On dira qu’une société ancienne utilisait des grands nombres si l’on peut démontrer qu’elle avait la capacité d’exprimer tous les entiers naturels jusqu’au plus petit des entiers que l’on peut qualifier de grand nombre ; un entier est dit grand nombre si et seulement si son écriture polynomiale, Σc_iN_i, exigerait, dans la/les « base(s) » habituelle(s) de cette culture [1], ‘plusieurs’ monômes. Pour démontrer qu’une société utilisait des grands nombres, il faut trouver au moins un cas de nombre dont l’écriture contient ‘plusieurs’ chiffres significatifs [2]. Pour les anciennes cultures mésoaméricaines, un nombre sera dit ‘grand’ si son expression vigésimale comprend au moins cinq ‘chiffres’ affectant les nœuds : 20⁰, 20¹, 20², 20³, et 20⁴, ou les périodes : jour, vingtaine, an (de compte), vingtaine d’ans, quatre-centaine d’ans. L’usage mésoaméricain des grands nombres remonte aux premiers Comptes longs, CL, attestés dès le 1^er siècle avant J.-C. Un CL est une chaîne de cinq chiffres (de 1 à 19) qui représente, de l’avis des spécialistes, une durée exprimée en nombre de jours et à l’aide d’une numération quasiment [3] du type ‘Position’ ; il s’agit, plus concrètement, du nombre de jours écoulés depuis l’origine de la chronologie en vigueur dans la culture considérée, à savoir le 11/08/-3113 pour les Mayas (avec la constante 584 283). Un calcul montre que les premiers CL écrits par les Mayas ou leurs voisins (stèles : 2 Chiapa de Corzo, C Tres Zapotes, 5 Takalik Abaj, 1 La Mojarra…) dépassaient le million de jours [4].

Figure 1

Stèle 19 de Uaxactun montrant, comme la stèle 18, le CL 8-baktun 16-katun 0-tun 0-uinal 0-kin, correspondant à la date grégorienne 01/02/357
(constante de correlation 584283)

Les sources offrent quelques CL olmèques, beaucoup de CL mayas, mais aucun CL aztèque, mixtèque ou zapotèque. On en déduit que dès l’époque classique, les Mayas furent sans doute les seuls véritables utilisateurs mésoaméricains des grands nombres ; des grands nombres qui représentaient des durées, et qui s’exprimaient par le nombre de jours écoulés depuis l’origine de la chronologie maya jusqu’à la date de l’événement considéré et ainsi daté par un CL.

En dehors des questions de calendrier, un autre domaine d’expérience délivre de possibles grands nombres : celui de l’administration des affaires publiques. Dans l’état actuel des recherches archéologiques et épigraphiques, cet usage est essentiellement [5] prouvé par les tequiamatl du monde aztèque. Ce sont des listes de tributs qui fournissent, cité par cité, des renseignements sur les tributs qu’il fallait remettre à la Triple Alliance [6] : nature [7], fréquence et quantité de chaque tribut.

Dans ces registres, les quantités furent écrites en numération vigésimale et additive (comme les numérations romaine ou égyptienne). Dans ce type de numération, pour écrire trois on répète trois fois le signe un et pour écrire deux cents, c’est-à-dire dix vingtaines, on répète dix fois le signe de la vingtaine, et ainsi pour les deux autres nœuds de la numération.

Figure 2

Matrícula de Tributos, lámina 29 montrant un tribut de 8 000 paquets de résine de copalme, et le tout de cette expression pictographique est deux fois glosé, en nahuatl : cenxiquipili xochocotzotl, et espagnol : una talega de ocozote o goma de color.

Par exemple, dans la Matrícula de Tributos, le plus grand nombre d’objets exigés s’élève à 8 000 ; cette quantité apparaît sept fois (lámina 6, 7, 16, 17, 22 et 29). Le signe ‘8 000’ (figuré par un ‘sac’ - Figure 2 ci-dessus ) de la lámina 29 est clairement associé au signe du paquet de résine de copalme, et le tout de cette expression pictographique est deux fois glosé, en nahuatl : cenxiquipili xochocotzotl, et espagnol : una talega de ocozote o goma de color. Soit, par ex., les gloses des tributs des p. 14, 22 et 32 (Figure 3 ci-dessous):

Figure 3

a. Macuilzontli iztacomitl b. Mattlactzontli tenextli c. Centzontlamamalli chili
Ontzontlamamalli ichcatl

Matrícula de Tributos, lámina 14, 22 et 32, montrant les gloses nahuatl de l’écriture pictographique des tributs

Les gloses nahuatl (en rouge sous la figure) permettent de découvrir que l’écriture pictographique reflète le fait que le nahuatl est une langue à classificateurs numériques (comme les langues mayas ou le chinois) et qu’il y avait plusieurs façons d’écrire les chaînes à coefficients plus grands que 2 (d’où répétition du nœud) : soit, le plus souvent, on répète autant de fois que nécessaire le tout constitué par le signe du nœud et le signe indiquant le caractère comptable et la nature du tribut ; soit, moins fréquemment [8], on répète autant de fois que nécessaire le signe du nœud et on place ce coefficient numérique complexe en position de déterminant du signe non répété qui indique le caractère comptable et la nature du tribut. On a donc deux structures :

[400 Cs + 400 Cs + 400 Cs + 400 Cs + 400 Cs] = 2000 (ou 5×400) Cs
[(400 + 400 + 400 + 400 + 400) + (400 + 400 + 400 + 400 + 400)] Cs = 8000 (ou 5×400 + 5×400) Cs

où C désigne le classificateur et s la nature du produit (du sel) ; ce qui permet de distinguer les deux sémiotisations de la troisième figure où l’on a d’une part 400 Cc (où c = du chili) et d’autre part (400 + 400) Ct (où t = du coton).

Figure 4

Codex Telleriano-remensis, folio 38v, montrant le nombre vingt mille en numération aztèque de type Addition 8000 + 8000 + 400 + 400 + 400 + 400 + 400 + 400 + 400 + 400 + 400 + 400

Un autre exemple de nombre relativement important est celui des victimes sacrifiées pendant la célébration du feu nouveau de l’an 8 Acatl (1487) et à l’occasion de l’inauguration du Templo mayor de Tenochtitlan. Cette fois, c’est un nombre à 2 ‘chiffres’ vigésimaux, les chiffres 2 et 10 qui sont respectivement coefficient (on répète deux fois) du nœud 8 000 et coefficient (on répète dix fois) du nœud 400. Il y aurait donc eu 2 × 20³ + 10 × 20² = 20 000 victimes.

Le type additif de cette numération écrite ne facilite pas vraiment la lecture/écriture des nombres à beaucoup de chiffres significatifs surtout quand ceux-ci sont eux-mêmes plus grands que la limite (4-5) de la capacité de l’oeil à subitiser le cardinal d’un ensemble. Sauf erreur de lecture, la Matrícula contient 260 entiers désignant des quantités de tributs, toutes comprises entre 10 (représenté par dix occurrences du signe de l’unité) et 8 000 (représenté par une occurrence du signe du nœud 20³). Tous les tributs enregistrés sont des nombres à un nœud (un seul chiffre significatif) ; tous les nœuds sont représentés par une ou plusieurs occurrences de leur signe. L’unité un et les trois nœuds valant puissances de vingt sont tous représentés dans ce corpus.

Théoriquement chaque signe peut être répété jusqu’à dix-neuf occurrences (correspondant aux 19 chiffres nécessaires en « base » vingt). De fait, dans la Matrícula, on ne trouve que : a) des nœuds seuls ou b) des chaînes comprenant 2, 3, 4, 5 ou 10 occurrences du même nœud. Ce qui revient à dire que, dans ce codex, les quantités de tributs sont sémiotisées par des nombres à un seul chiffre et que le choix de ce chiffre est contraint puisque seuls sont attestés les chiffres 1, 2, 3, 4, 5 et 10. Voici le tableau donnant le nombre total de tributs marqués par des entiers de la forme c_i20ⁱ. Par ordre de fréquence, on trouve :

c_i 20ⁱ	1	2	3	4	5	10	160 fois le nombre 400 (le plus fréquent) ; 43 fois le nombre 20 ; 13 fois le nombre 800 ; 9 fois le nombre 1200 ; 7 fois les nombres 80 et 8000 ; 6 fois le nombre 40 ; 4 fois le nombre 1600 ; 3 fois les nombres 100, 200 et 4000 ; 1 fois les nombres 10 et 2000.
20⁰	0	0	0	0	0	1
20¹	43	6	0	6	3	3
20²	160	13	9	4	1	3
20³	7	0	0	0	0	0
20⁴	210	19	9	11	4	7

Au total, il y a 210 entiers représentés par un seul signe (nœud non répété) et 50 entiers représentés par des répétitions de signes de nœud : 19 coefficients deux (deux occurrences du même nœud), 9 coefficients trois (trois occurrences), 11 coefficients quatre (quatre occurrences), 4 coefficients cinq (cinq occurrences) et 7 coefficients dix (dix occurrences d’un même signe de nœud).

Ce qui tend à prouver que les Aztèques en charge de l’impôt avaient une préférence pour :

a) éviter les nombres à plusieurs chiffres significatifs (pas de grands nombres)
b) utiliser seulement des nombres à un ou deux chiffres,
c) utiliser seulement les chiffres petits (1, 2, 3, 4) ou égaux aux ‘sous-bases’ (5 et 10).
Ce qui semblerait indiquer que les dirigeants de la Triple alliance étaient davantage intéressés par les ordres de grandeur que par les subtilités d’un calcul exact à l’unité près. L’arrêt (au cube 20³) du paradigme des puissances de vingt a souvent été signalé parce que ce fait permet d’estimer la capacité générative théorique de la numération écrite aztèque [9].

"On ne saurait du reste oublier que les aztèques n'ont jamais écrit de nombres égaux ou supérieurs à 20⁴ = 160 000" (Guitel;1975:139)

La formule est un peu brutale, puisqu’il faudrait dire : les archéologues et les épigraphistes n’ont jamais découvert (jusqu’à ce jour) un nombre supérieur à 160 000 écrit par les Aztèques avant la colonisation.

Elle conduit néanmoins à relever une différence d’usages du nombre, d’un côté, chez les Mayas du Classique (pour établir de nombreuses égalités calendaires), de l’autre, chez les Aztèques (pour administrer la vie publique) ; une différence qu’il est toujours regrettable d’interpréter en termes de supériorité/infériorité des cultures comparées :

"On ne peut mettre en doute que les capacités mathématiques des Aztèques et des Mayas étaient de qualité très différente (…) Pour un mathématicien, le contraste entre l'usage du calendrier par les mayas et (…) par les aztèques fait penser que ceux-ci n'ont été que des imitateurs de la science maya ou d'une science antérieure." (idem)

Ce jugement de Guitel contient des éléments qui pourraient être versés au dossier des circonstances limitant l’usage des grands nombres chez les Aztèques, voire au dossier de l’absence, dans les documents qu’ils ont laissés, de Comptes longs, d’égalités calendaires et plus généralement de grands nombres (au sens de la définition précédente).

Dire que la numération écrite aztèque était de type additif (en rappelant que ce type ne facilite ni l’écriture des grands nombres ni le calcul arithmétique notamment des divisions) ne préjuge en rien des qualités de la numération parlée nahuatl (type ‘Articulation’) ni de la capacité des scribes aztèques intéressés à se doter des meilleurs outils de calcul disponibles en Mésoamérique : la numération vigésimale de position des codex mayas. Retenons de ce coup d’oeil l’idée que les savoirs aztèques s’inscrivent dans un riche fonds mésoaméricain et précolombien de recherches arithmétiques et d’observations astrologiques.

Ce fonds provient vraisemblablement de l’antiquité olmèque [10]. Il fut fortement enrichi, à l’époque classique, par les Mayas [11]. Enrichissement résultant de leurs efforts d’appliquer le nombre à des problèmes de calendriers et d’éphémérides ; des problèmes qui semblent ne pas avoir spécialement déclenché l’intérêt des Aztèques plus enclins apparemment à s’intéresser aux questions de comptabilité économique que de comput calendaire. Dès lors, il est banal de constater que les Mayas ont produit plus de résultats arithmétiques que les Aztèques, mais il reste utile de préciser que c’est dans le domaine du comput calendaire et pas dans celui de l’administration des affaires publiques.

Occupés par les questions de calendrier, on peut penser que les Mayas investirent moins d’efforts que les Aztèques dans le domaine de la comptabilité. De fait, pour les Mayas de l’époque classique, les recherches archéologiques et épigraphiques n’ont pas découvert d’équivalents des tequiámatl aztèques indiquant fréquence, nature et quantité de tributs. Certes, l’iconographie maya livre des scènes de remise d’objets qui nous semble plus proches de la pratique du don/contre don que d’une véritable politique étatique de l’impôt. Par exemple, la scène du vase K5453 (Figure 5 ci-dessous) montre un sac au pied du dirigeant assis ; on lit ‘3 CAUAC CAUAC-’ ou ‘3 PIC-’ et on traduit ‘tribut de 3 x 400 ou de 3 x 8 000 cabosses de cacao ( ?)’. Comme dans le cas aztèque, cette inscription n’est pas un exemple de grand nombre dans la mesure où c’est un nombre ‘rond’ à un seul chiffre significatif.

Figure 5
	Vase maya de la collection Kerr, K5453, montrant une scène de remise d’impôts (fig. 5a) et comme détail de cette scène (fig 5b) un impôt en ‘monnaie’ de cacao s’élevant à 3 CAUAC CAUAC de cabosses.

Ce qui montre que le nombre aztèque était – bien davantage que le nombre maya – au service de l’administration publique du ‘budget de l’empire’. Herbert R. Harvey et Barbara Williams (1981) ont développé la thèse que les Aztèques furent particulièrement innovants dans ce domaine, au point d’avoir développé à l’époque coloniale l’usage du calcul des tributs en proportion des surfaces cultivées (dans des champs de forme polygonale) ellesmêmes évaluées par un calcul sur les dimensions des côtés. Admettons [12].

2. Equations et grands nombres mésoaméricains

Pour l’épistémologue, il est frappant de constater que la pratique de l’enregistrement des tributs n’a pas conduit les Mésoaméricains qui s’y employèrent à systématiser l’écriture des grands nombres et à jeter les bases d’une science de la comptabilité proprement dite. Une comptabilité qui ne se serait pas contentée de dresser l’inventaire des tributs, mais qui se serait attachée à les totaliser, voire à croiser plusieurs façons de les totaliser. Car une liste d’inventaire n’est pas une comptabilité, si on pose que le degré zéro d’une comptabilité à naître et développer est d’avoir le moyen de détecter les erreurs et, mieux encore, au degré un, d’avoir le moyen de corriger les erreurs détectées.

La recette pour y parvenir est connue. On commence par introduire de la redondance (clé de numéro de sécurité sociale, bit de parité, etc.). Puis par croiser astucieusement deux sortes de redondance. Les tableaux comptables sont de bons exemples : ils permettent d’articuler les totalisations par ligne et les totalisations par colonnes.

Dans ce point de vue, il devient frappant de constater un contraste entre : a) l’absence de mise en relation des quantités de tributs dans les pratiques comptables mésoaméricaines [13] et b) l’abondance des mises en relation des dates et des durées dans les pratiques calendaires et astronomiques dès les plus anciennes pratiques olmèques ou mayas de datation en CL.

Les champions de ces mises en relation sont à coup sûr les Mayas depuis l’époque classique jusqu’à l’époque des codex et particulièrement du codex de Dresde. Il n’est pas exagéré de dire que les Mayas nous ont laissé des milliers d’équations reliant des dates et des durées. Petites ou grandes, ces durées sont exprimées en nombre de jours ou en nombre de diverses périodes (lunaisons, mois, années…) ; par ailleurs, ces durées montrent que les scribes savaient jouer sur la dualité ordinal/cardinal du nombre pour traduire une durée (aspect cardinal) en date (aspect ordinal) et vice-versa.

Les codex mayas contiennent des dizaines d’almanachs lesquels démontrent que les scribes avaient l’habitude de se déplacer dans le cycle des 260 jours de un ‘almanach divinatoire’ encore appelé ‘année/semaine religieuse’. Dans le but d’énoncer un présage, le scribe se déplace par saut de diverses amplitudes et va ainsi de date en date, chacune pouvant être bénéfique/maléfique/indifférente. Ces pratiques divinatoires sont encore attestées plus ou moins sporadiquement aujourd’hui. Prenons par exemple la page 2d du codex de Dresde.

Le texte [14] glose l’iconographie montrant Ik Uh, jeune déesse de la Lune, et Kisin, dieu de la mort ; il traite les premières stations comme favorables et les secondes défavorables.

Assez elliptique, l’agencement typographique [15] des dates et des durées de cette page montre une ligne d’entiers alternativement peints en rouge et en noir, et une colonne de 5 dates de la forme αX (α est en ‘facteur commun’) où α = 13 et X = Lamat, Ahau, Eb, Kan, et Cib.

Les nombres noirs sont écrits en numération additive (type romain [16]), et ils sont placés entre deux dates α [X] dont le rang a est seul marqué en rouge et le nom X étant sous-entendu. En fait, sont sous-entendues cinq lignes de dates α [X] dont les noms X sont à rétablir pour compléter les cinq lignes de dates 2 [X] et 13 [X]. La suite alternée rouge/noir [17] 13 X, 28, 2, 24, 13. se lit par exemple à partir du signe X = Ahau : 13 Ahau, 28, 2, 24, 13. Les spécialistes rétablissent les éléments sous-entendus « 13 Ahau [+] 28 [=] 2 [Lamat] [+] 24 [=] 13 [Eb] » et expliquent qu’en partant d’un 13 Ahau, on arrive en 28 jours à un 2 [Lamat], d’où, en 24 jours, on arrive à 13 [Eb].

Figure 6

Codex de Dresde, p. 2d montrant le début d’un almanach divinatoire, et la mise en page de chaînes d’équations temporelles de la forme α_i [X_i] + d_i = α_j[X_j]

L’almanach contient en particulier des chaînes d’égalités qui représentent des translations de pas d_i (durées en jours) qui font passer des dates α_i[X_i] aux dates α_i+1[X_i+1] ; soit des égalités du type « α_i[X_i] + d_i = α_i+1[X_i+1] ». Le texte et l’iconographie précisent le caractère favorable, défavorable ou indifférent des stations atteintes : l’almanach est un instrument de divination. Comme le montrent les stèles 18 et 19 d’Uaxactun [18], le même habitus (former des égalités combinant les deux aspects du nombre) est attesté en dehors des almanachs. On le trouve aussi dans les tables de multiples du codex de Dresde et dans les textes historiques des monuments. Dans ces exemples, l’habitus n’est pas limité aux petits déplacements écrits en numération additive : les CL sont en numération de position ou disposition et la notation des dates est plus complexe puisque l’indication de la date αX dans le cycle du tzolkin de 260 jours est accompagnée de la date βX dans l’année vague solaire ha’ab de 365 jours et parfois de données relatives au cycle lunaire voire vénusien.

Monuments et codex prouvent que les Mayas écrivaient couramment des nombres à cinq chiffres significatifs et qu’ils pouvaient poser et résoudre des équations calendaires faisant intervenir des durées dépassant le million de jours (et la limite aztèque 160 000). Par ex. les linteaux 29, 30 et 31 de Yaxchilan contiennent le CL 9-baktun 13-katun 17-tun 12-uinal 10-kin = 9 x 144 000 + 13 x 7 200 + 17 x 360 + 12 x 20 + 10 = 1 395 970 et quatre Nombres de distance (-397, 15 230, 4 320 et 2 520) ; ces durées relient l’origine à 5 dates Calendar Round – CR de la forme αX βY (cf. Encart 2) – du règne du roi Oiseau-Jaguar ; soit la chaîne :

[0.0.0.0.0. 4 Ahau 8 Cumku] + 9.13.17.12.10. = [9.13.17.12.10.] 8 Oc 13 Yax
[9.13.17.12.10. 8 Oc 13 Yax] – 1.1.17. = [9. 13. 16. 10. 13.] 1 Ben 1 Ch’en
[9. 13. 16. 10. 13. 1 Ben 1 Ch’en] + 2.3.5.10. = [9. 16. 1. 0. 0.] 11 Ahau 8 Tzec
[9. 16. 1. 0. 0. 11 Ahau 8 Tzec] + 12.0.0. = [9. 16. 13. 0. 0.] 2 Ahau 8 Uo
[9. 16. 13. 0. 0. 2 Ahau 8 Uo] + 7.0.0. = [9. 17. 0. 0. 0.] 13 Ahau 18 Cumku
Enfin, l’indication ‘Fin du Katun 17’ indique la date CL atteinte 9.17.0.0.0.

Figure 7

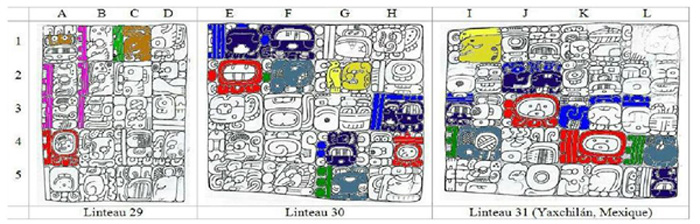Yaxchilan, Mexique, linteaux 29,30 et 31 narrant les exploits du roi Oiseau-Jaguar et la mise en page de chaînes d’équations temporelles de la forme α_iX_i β_iY_i + Σc_iP_i = α_jX_j β_jY_j où les αX βY sont des dates CR reliées par un CL ou des nombres de distance Σc_iP_i

La comparaison de ce texte avec une chronique aztèque (codex Telleriano Remensis - Figure 8 ci-sessous) montre que les scribes aztèques dressaient des listes d’années (sur la figure, les années successives : 6 Calli/1485, 7 Tochtli/1486, 8 Acatl/1487) pour y inscrire les événements mais sans les relier, comme les Mayas, par des équations jouant sur la dualité date/durée.

Figure 8

Codex Telleriano Remensis, folio 38 verso, narrant l’arrivée au pouvoir de Ahuitzotl, l’inauguration du Temple, la célébration du feu nouveau.

L’étude des équations mayas montre que les scribes distinguaient les aspects du nombre. Le point de vue ordinal pour distinguer une entité parmi d’autres [19], le point de vue cardinal pour définir une entité par son étendue [20]. Elle montre aussi qu’ils n’ont jamais confondu les marques de l’ordinal et du cardinal, par ex. le trait de couleur, rouge/noir, dans l’opposition date/durée, ou la différence des logogrammes dans l’opposition du zéro ordinal/cardinal...

3. Les numérations parlées et écrites

3.1 Les chiffres des numérations parlées et écrites aztèques et mayas

A l’écrit, les chiffres aztèques [21] sont des files de points. A l’oral, les numéraux inférieurs au nœud vingt sont des atomes (1, 2, 3, 4, 5, 10, 15) ou des composés additifs comprenant : un appui additif (5, 10 ou 15) [22] en place de 1er argument et un atome (1, 2, 3 ou 4) en place de 2^nd argument. Entre 11 et 19, l’expression additive contient le relateur om/on (Cf. tableau 1 ci-dessous) [23].

Tableau 1

	ce	ome	eyi	nahui
ma-cui-li	chuicua-ce	chic-ome	chicu-eyi	chicu-nahui
ma-tlac-tli	matlactli on-ce	matlactli om-ome	matlactli om-eyi	matlactli on-nahui
caxtol-li	caxtolli on-ce	caxtolli om-ome	caxtolli om-eyi	caxtolli on-nahui

Figure 9
	8	9	10
	13	14	15
	18	19	21
Un extrait du Codex Duran montrant les « chiffres » 8, 9, 10, 13, 1, 15, 18, 19, 21

Muni de cette addition, l’ensemble des chiffres parlés nahuas est isomorphe à l’ensemble des chiffres écrits de style point/barre (Cf. Tableau 2 ci-dessous). Bien que mésoaméricains [24], les chiffres point / barre ne furent pas en usage chez les Aztèques. Ils sont formés par répétition du point et de la barre [25] puis par composition additive des éléments répétés.

Tableau 2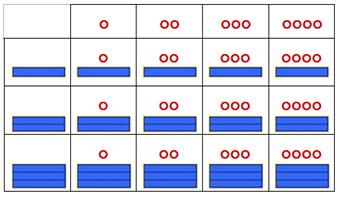

Tableau des chiffres mésoaméricains (qui n’étaient pas en usage chez les Aztèques) montrant le système répétitivo-additif de leur formation

Chez les Mayas, les petits numéraux parlés (< 20) sont des atomes (1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12) ou des composés additifs sur un seul nombre d’appui, 10 , en place de 2^nd argument, le 1^er argument étant saturé par un atome de (3, 4, 5, 6, 7, 8, 9) ; en d’autres termes, l’ensemble des ‘chiffres’ des numérations parlées mayas n’est pas structuré comme l’ensemble répétitivo-additif des chiffres mésoaméricains écrits de style point/barre. Voici un tableau des entiers de 1 à 19 en numération parlée yucatèque et orthographe coloniale :

Tableau 3

hun	ca	ox	can	ho	uac	uuc	uaxac	bolon	lahun
1	2	3	4	5	6	7	8	9	10
		oxlahun	canlahun	holahun	uaclahun	uuclahun	uaxaclahun	bolonlahun	buluc	lahca
		13 (3+10)	14 (4+10)	15 (5+10)	16 (6+10)	17 (7+10)	18 (8+10)	19 (9+10)	11=? (9+2)	12=? (10+2)

Tableau des expressions numérales yucatèques formées additivement sur le nombre d’appui ‘dix’ et suivant le modèle 3 + 10 = 13

Ce tableau met en évidence la structure additive. Il suggère aussi que 11 et 12 seraient des anciens composés devenus opaques [26]: buluc < *bolon + ca = 9 + 2 (qui suggère : lahun = *bolon + hun = 9 + 1) et lahca < lahun + ca = 10 + 2. L’ensemble des chiffres ‘parlés’ mayas n’est donc pas isomorphe à l’ensemble des chiffres écrits mayas et mésoaméricains de style point/barre. A ceci près, que les Mayas ont aussi utilisé un autre jeu de chiffres écrits. Il s’agit de chiffres que l’on pourrait dire ‘solennels’ car destinés à l’affichage sur les stèles et les monuments. Ces chiffres ont la forme d’un personnage (‘zéro’ à gauche, ‘neuf’ à droite). En général, ces 20 chiffres sont représentés par la tête du personnage (synecdoque de la figure entière), c’est le style céphalomorphe.

Figure 10

A gauche : zéro sous forme entière et sous forme de tête.
A droite : chiffre 9 sous forme entière et sous forme de tête (avec taches de jaguar)

L’observation de l’ensemble des chiffres écrits mayas montre :
a) une innovation essentielle, celle du chiffre zéro, attesté dès le 4^ème siècle et dont plusieurs variantes sont aujourd’hui connues (cf. Figure 11 ci-dessous).

Figure 11

(a)

(b)

Diverses formes du zéro cardinal sur les monuments (a) et dans les codex (b) ; contrairement aux formes (b) de l’écriture des codex, les formes (a) c’est-à-dire les formes ‘solennelles’ de l’écriture monumentale ne sont pas indépendantes mais préfixées à un glyphe de période (jour, mois, année, etc.)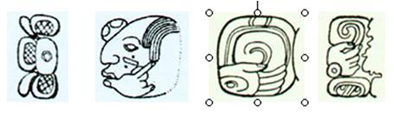

b₁) une règle additive concaténant, en style céphalomorphe et en numération parlée, un entier de l’intervalle [3, 9] et le nombre d’appui additif 10
b₂) un procédé métonymique qui consiste en style céphalomorphe à réduire le crâne caractéristique de l’entier 10 à sa mâchoire décharnée ; ce qui permet d’implanter le nombre dix dans la tête des chiffres entrant dans les composés additifs ainsi sémiotisés selon le schéma « 5 + 10 = 15 » (cf. Figure 12).

Figure 12

(a) (b) (c)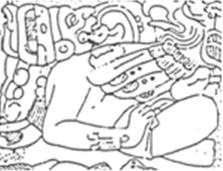

Figures entières des entiers cinq (a), dix (b) et quinze (c) et illustrant par l’exemple de quinze la formation des composés additifs de l’écriture monumentale ; dans le chiffre 15, le nombre d’appui dix est représenté par la mâchoire décharnée de la figure du dix –synecdote du personnage b) – insérée dans la tête a) de l’entier cinq dont l’un des traits caractéristique est le ‘chapeau’.

c) les entiers 1, 2 et 11, 12 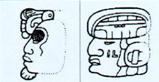ne semblent pas composés du moins d’une manière transparente pour le lecteur d’aujourd’hui.
Autrement dit, l’ensemble des chiffres solennels mayas non nuls est structuré par une loi d’addition qui calque exactement celle des chiffres ‘parlés’ des langues mayas. Ces deux ensembles sont isomorphes. Voici les céphalomorphes des intervalles [3, 9] et [13, 19] (cf. Figure 13 ci-dessous).

Figure 13

(a) (b) (c)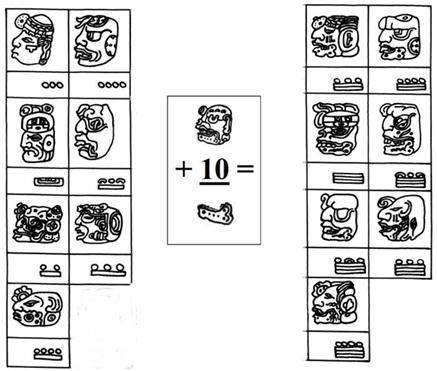

(a) les céphalomorphes de 3 à 9, (b) les formes entière (crâne) et réduite (mâchoire) de l’entier dix, et (c) les composés additifs de 13 à 19 construits sur le modèle 3 + 10 = 13.

3.2 L’ensemble des nœuds des numérations parlées : détermination à valeur multiplicative

Dans les deux univers culturels, maya et aztèque, l’analyse de la forme des nœuds [27] de la numération parlée montre qu’ils relèvent d’un processus de détermination où interviennent[28] un déterminant numéral (dont le référent est un entier inférieur à vingt [29]) et un déterminé numéral (son référent est un nombre d’appui multiplicatif) que l’on trouve respectivement en position de 1^er et 2^nd argument du numéral complexe signifiant du dit nœud. Couramment les déterminés renvoient aux trois nœuds principaux des numérations mésoaméricaines : le nœud 20 (souvent dit ‘base’), son carré 400 et son cube 8 000.

Launey (1986:665) souligne, pour le nahuatl, qu’il ne « connaît pas d’expression classique désignant des puissances de 20 supérieures à 8000 (20³) » et ceci malgré le témoignage d’un contemporain qui lui aurait affirmé que la suite des puissances de vingt continue au-delà de 8 000. On doit donc retenir que la numération parlée aztèque comprend seulement les trois nœuds[30] « 20¹, 20² et 20³».

Chez les Mayas du Classique la suite des puissances successives ne s’arrête pas au cube. On sait au contraire que les scribes l’ont effectivement prolongée bien au-delà de la troisième puissance. Dans le cas des durées exprimées en nombre de jours, la stèle 1 Cobá prouve que, la série maya des puissances de vingt est montée aux environs[31] de la 20^ème.
La rareté et l’état de conservation des cas de nombres dépassant les nombreux CL à cinq chiffres n’a pas permis de découvrir les noms de toutes ces puissances dans les langues mayas. C’est pourquoi les américanistes utilisent par commodité une sorte de métalangage constitué des noms yucatèques connus par les documents coloniaux pour les plus petites puissances, et pour le reste des dénominations construites par continuité : hun kal ‘un vingt = 20¹’, hun bak, ‘1×20²’, hun pic, ‘1×20³’, hun calab, ‘1×20⁴’, hun kinchil, ‘1×20⁵’, etc.
En numération aztèque, les restrictions observées (cf. p. 4 c) à l’écrit le sont aussi à l’oral. Ci-dessous le tableau des déterminations aztèques que l’on peut dresser à partir des données de Launey [32] en prenant comme déterminés les nœuds 20¹, 20² et 20³ : cem-pohualli ‘un compte’, cen-tzontli ‘une (touffe de) cheveux’ et cem-xiquipilli ‘un sac (de graines)’

Tableau 4

1	(ou \| )	cem-
2		om-/on-
3		c-
4		nauh-		-pohualli		20¹=20
5		macuil-	×	-tzontli		20²=400
10		matlac-		-xiquipilli		20³=800
15		caxtol		forme parlée	forme écrite
6,7,8,9,11,12, 13,14,16,17,18,19	etc.	?

Tableau de gauche (d’après Launey) : déterminants (de 1 à 19) des nœuds aztèques ‘vingt’, ‘quatre-cent’ et ‘huit-mille’ bien attestés par les documents ; la deuxième colonne montre, pour rappel, la forme point/barre de ces déterminants répandue en mésoamérique depuis le milieu du premier millénaire avant J.-C. mais que les Aztèques n’utilisaient pas (les ‘chiffres’ aztèques sont des files de points jusqu’à dix-neuf inclus).
Tableau de droite : formes parlées et écrites des trois nœuds de la numération aztèque.

Attention à ne pas mésinterpréter les colonnes de glyphes (multiplicateurs et nœuds) en écriture pictographique : elles ne servent qu’à montrer la transcription en signes d’écriture d’une part des multiplicateurs (déterminants) en chiffres mésoaméricains point/barre, et, d’autre part, des nœuds (déterminés) en signes aztèques. Ce serait une erreur de penser que les expressions complexes parlées, par exemple nauh-pohualli, s’écrivaient en juxtaposant les deux signes correspondants et .
Cette concaténation n’existe tout simplement pas chez les Aztèques dont la numération écrite était de type additif comme la numération en chiffres romains. Le nombre parlé nauh-pohualli ‘quatre-vingts’ se traduit à l’écrit par 4 occurrences du nœud 20 comme sur la Figure 14 ci-dessous dont les gloses précisent la lecture : a) en nahuatl nauh-tecpantli tepoztli et b) en espagnol instrumentos de yerro para cortar.

Figure 14

Extrait de la Matrícula de tributos montrant l’écriture du nombre parlé nāuh-pōhualli ‘quatre-vingts’

En numérations écrites mayas et contrairement aux restrictions notées en numération écrite aztèque, tout entier de [1, 19] est attesté comme coefficient de tout nœud, ceci au moins jusqu’au baktun (20⁴). De nombreux exemples (Comptes longs et Nombres de distance) le démontrent. Le paradigme est complet, de hun ‘1’ à bolonlahun ‘19’, tant pour les chiffres point/barre que céphalomorphes, tant en usage cardinal qu’ordinal. Ce qui nous invite à regarder comment les numérations écrites mayas et aztèques notaient ces conceptualisations numériques qui correspondent pour le mathématicien à la notation des monômes c_iN_i. C’est sur ce point de la sémiotisation des déterminations c_iN_i que les systèmes mayas et aztèques divergent le plus, car les numérations mayas ne sont pas du type additif. Chez les Mayas, les multiples des nœuds s’écrivent comme ils s’énoncent sous forme de déterminations à valeur multiplicative : leur 1er argument est un chiffre notant un coefficient et le 2^nd un nœud/classificateur/période (non marqué en numération de position). La différence est spectaculaire : un aztèque écrit ‘VINGT VINGT VINGT VINGT-’ et énonce ‘quatre VINGT-’ là où un maya écrit ‘4 VINGT-’ et énonce ‘quatre VINGT-’. Attention à ne pas confondre, chez les Mayas, l’écriture générale des nœuds et la notation écrite spécialisée à l’enregistrement de l’âge de la Lune dans les séries lunaires ; par nature ou définition, cette écriture est seulement attestée pour les entiers de 21 à 29 où elle est motivée par la forme protractive orale [33] de ces nombres, par exemple 26 = (6 → 20) (cf. Tableau 5).

Tableau 5

	Composition (+) mésoamérique	Protraction (→) maya	Détermination (x) maya	Répétition (+) aztèque
Ecrite
Parlée beltran	ox lahun	wak [tu-ka'-] k'aal uac tu kal	kan winik/ha'ab can katun	nauh pohualli '4 vingt'
Décimale	13 = 3+10	26 = 6 → 2° vingt	80 = 4 vingt = 4 × 20 = 20 + 20 +20 +20

Comparaison de quatre types de formation numérique (addition mésoaméricaine, protraction maya, multiplication maya et répétition aztèque) et leurs réalisations en numération écrite, parlée [34] et décimale.

3.3 Les numéraux de plus grande profondeur syntaxique

En numération parlée nahuatl, l’expression numérale des entiers intermédiaires entre les nœuds et leurs multiples est une suite additive d’opérandes que schématise la formule algébrique n = Σ c_iN_i. Exemple : om-pohualli on ce = [(2 × 20) + 1] = 41.
A cette ‘profondeur syntaxique’, les expressions numérales sont très systématiques [35] en nahuatl. De plus, les scribes aztèques disposaient de deux particules [36] qui leur donnaient la possibilité de distinguer l’addition des opérandes et l’addition des constituants d’un chiffre : caxtolli on-nahui pohualli ipan mátlactli om-ome = [(15 + 4) x 20] ⊕ [(10 + 2)] = 392.
D’où la thèse que la numération parlée nahuatl est du sous-type arithmétique ‘parenthésé’ (Cauty;1984) ou du type Bien organisé (Guitel;1975) encore dit type [37] Articulation (comme celle des Chinois ou des Coréens) et que nous qualifions parfois de dispositionnelle.
La numération parlée [38] n’est donc pas du type Additif de la numération écrite, ce qui revient à dire que les numérations aztèques, parlées et écrites, ne sont pas isomorphes.
Par contre, la numération parlée des Aztèques est isomorphe à la numération des CL gravés sur les monuments mayas du Classique. Du point de vue cognitif, le nombre est conçu en logique polynomiale [39]. Du point de vue de la sémiotisation, le scribe exprime tous les monômes de Σ c_iN_i – quand le chiffre zéro est disponible (c’est le cas des Mayas) – et seulement les monômes à coefficient non nul – quand le zéro n’est pas disponible ou utile (c’est le cas des Aztèques) –. La numération parlée nahuatl et la numération du CL diffèrent peu de la numération de Position (au sens strict) [40] attestée par les codex mayas du Postclassique.

Chez les Mayas, les numérations parlées et écrites ne sont pas non plus isomorphes entre elles. La différence vient du fait que l’expression parlée des entiers intermédiaires, ceux qui se trouvent entre les nœuds et leurs multiples, est d’un type particulier. Nous avons montré (Cauty;1987) que les numérations parlées des langues mayas, notamment en yucatèque et en chol, étaient jusqu’à l’époque coloniale d’un type assez peu attesté dans le monde, le type Protraction (Cauty et Hoppan, 2007) [41].

Les numérations protractives saisissent le nombre plus en vision ordinale que cardinale. Pour exprimer 35, par exemple, le locuteur doit anticiper le palier visé de la 2^ème vingtaine et, de manière rétrograde, le prédécesseur de ce palier, à savoir la 1^ère vingtaine. D’où la glose ‘5 vers la 2^ème vingtaine’ ou ‘5 vers 40’ de l’expression yucatèque holhu (ti u-) ca kal [42] de l’entier 35. Pour conclure cette partie, nous traduisons dans les différents systèmes de numération évoqués l’expression numérale du millésime de la révolution française 1789 supposé désigner des entités -t. En logique vigésimale, le décimal 1789_dix a 3 chiffres significatifs : [ ( 4 x 20² ) + ( 9 x 20¹ ) + 9 ] ou 4.9.9.

C’est la forme polynomiale que calquent les numérations écrites mayas (monuments et codex) et la numération parlée aztèque. La forme maya parlée est plus difficile à restituer non pas parce qu’elle est de type Protraction mais parce que la colonisation a eu pour effet d’en faire pratiquement disparaître les formes au profit d’autres, plus proches du modèle de la numération additivo-multiplicative du conquérant espagnol. Il est cependant possible de reconstruire la forme protractive de 1789. Soit → le signe de l’opération de protraction. En logique protractive : 1789 = [(4 x 400) ⊕ (9 → 5° 20)] pouvait s’énoncer « [(can bak-) catac (bolon- tu ho kal-)] t ».

Figure 15

Montrant un hypothétique nombre aztèque à trois chiffres significatifs 1789 = 4 x 400 + 9 x 20 + 9 unité.

Pour sémiotiser le même entier en numération additive aztèque, il faut répéter dans l’ordre ou le désordre, les signes des nœuds: 4 signes tzontli, 9 signes pohualli et 9 signes unité. L’écriture proposée ci-contre n’est pas tout à fait correcte : il manque un signe précisant la chose comptée (par ex. du temps discrétisé en jours), et elle a 3 chiffres significatifs (un de plus que dans les grands nombres aztèques que nous avons pu observer dans les documents). D’où le tableau de 1789 en écriture polynomiale, en numération parlée nahuatl et dans les deux numérations écrites mayas (monuments et codex) ; du point de vue cognitif, ces trois numérations sont quasi isomorphes : elles relèvent de la conceptualisation polynomiale [43] .

Tableau 6

Σ c_iN_i	[(4	×	20²)	⊕	(9	×	20¹)	⊕	9]	Unité
Parlée nahuatl	nauh-		-tzontli	ipan	chiucnahui		pohualli	ipan	chiucnahui	quahuitl
Maya monument
codage yucatèque	can		baktun	catac	bolon		katun	catac	bolon	tun
maya codex										20⁰
Parlée protraction	[(can		bak-)	catac			(bolon	→ tuy	hokal-	t)]

Forme écrite de l’entier 1789 : en écriture polynomiale, en numération parlée nahuatl et dans les deux numérations écrites mayas (monuments et codex) ; du point de vue cognitif, ces trois numérations sont quasi isomorphes : elles relèvent de la conceptualisation polynomiale.
Unité "quahuitl" - voir note [44].

4. Variation sur les chiffres et les classificateurs aztèques

Comme tout système, les numérations logographiques aztèques présentent des variations. En tout cas, à l’époque coloniale, il y a deux systèmes qui se distinguent nettement par la forme des signes de la vingtaine et de l’unité un. L’un est plus traditionnel et plus ancien, l’autre plus innovant et plus tardif. Aucun des deux n’utilise les chiffres mésoaméricains.

Figure 16

(a) (b)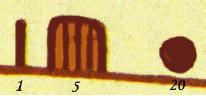

Formes aztèques de quelques entiers : (a) en numération écrite traditionnelle (1, 10, 20, 60, 400, 800), et b) en numération écrite tardive (innovation attestée par divers codex de l’époque coloniale, 1, 5 et 20.

Dans le système traditionnel (cf. Figure 16 (a)), le point est le signe de l’unité un, tandis que la vingtaine est marquée par une sorte de petit drapeau. Dans le système tardif, l’unité un est marquée par un trait, tandis que le point devient le rond et marque les vingtaines. En d’autres termes, le rond du système tardif correspond au drapeau du système traditionnel. Traditionnels ou tardifs, les signes peuvent être répétés, au moins théoriquement, jusqu’à dix-neuf occurrences. Dans le système tardif, quand il y a plus de cinq répétitions du signe de l’unité un, les occurrences sont clairement regroupées par paquet de cinq et un trait relie la première à la cinquième du groupe ainsi formé, ce qui leur donne l’allure d’un peigne [45]. Le tableau suivant illustre la différence des systèmes traditionnel et tardif pour la mise en signe des petits entiers compris entre 5 et 20 ; il montre aussi que la systématisation du regroupement par cinq a pour effet, dans le système tardif, de réduire le champ des lectures ou interprétations possibles d’une écriture (réduction de l’ambiguïté). Cf. Figure 17 ci-dessous.

Figure 17

Comparaison des petits entiers en numération aztèque traditionnelle et en numération écrite tardive

Contrairement au français et à l’espagnol qui sont des langues à pluriel, les langues nahuatl et mayas sont des langues à classificateurs. Dans une langue à pluriel, les substantifs comptables (c’est-à-dire la plus grande partie du lexique) conduisent à des énoncés du type numéral + nom concret, et on dit, en espagnol comme en français, 80 haches/hachas.
Dans les langues à classificateur, les mots désignent des notions (plutôt que ‘un enfant’, on entend ‘de l’enfant’) qui ne sont a priori ni pluralisables (comme par ex. le mot fraîcheur dans ‘je prends la fraîcheur’) ni quantifiables (je peux quantifier directement ‘une/deux pomme(s)’, mais pas ‘de la pomme’) avant d’avoir été soumis à une opération de détermination/substantialisation qui laisse une trace linguistique (à savoir un classificateur dans les langues où leur système est bien développé) : ‘je prends trois tranches de pain’. Les classificateurs se diversifient pour individuer de différentes manières une même notion et pouvoir distinguer/quantifier : ‘de la pomme, fruits, 3’ ou ‘de la pomme, arbres, 3’, ‘des gens, debout, 3’, ‘des animés non humains, gros, 3’, etc.

Ne voir que deux éléments (déterminant numérique + déterminé nominal) dans les énoncés comme ‘80 charges de cacao’ ou ‘100 haches’ résulte du fait que le français et l’espagnol sont des langues à pluriel qui ont peu ou pas développé de ‘classificateurs numériques’ [46].
Dans les documents traditionnels, par exemple la Matricula de tributos, les scribes notaient bien trois informations renvoyant à trois actes cognitifs différents : a) un acte de saisie de la nature du tribut, b) un acte d’individuation/détermination/prélèvement qui concrétise et rend comptable la notion dont on parle et que l’on veut quantifier, enfin c) un acte de comptage (énumération + dénombrement) qui s’achève dans l’acte de renseigner le codex en y portant trois marques qui témoignent de ce triple travail. Dans les exemples suivants, les gloses en nahuatl et en espagnol sont des clefs pour reconstituer les étapes du processus énonciatif. Elles sont comme les traces [47] laissées par un cheminement cognitif qui est passé par trois moments (identification du tribut, modalité du prélèvement, quantification).

Figure 18 Extraits de la Matricula de tributos montrant l’écriture numérique des quantités avec leurs gloses en nahuatl et espagnol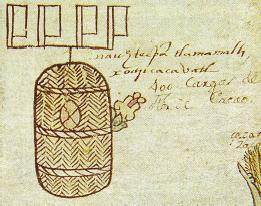
nauhtecpan tlamamalli xochicacahuatl	macuiltecpantli tepoztli	nauhtecpantli tepoztli
4 x 20 Classificateur fleur de cacao	5 x 20 Classificateur hache	4 x 20 Classificateur hache
100 (sic !) cargas de Flor Cacao	Pas de glose visible	Instrum. de yerro p.cortar
80 (100 ?) charges de fleurs de cacao	100 haches	80 haches

D’où la thèse que l’expression d’une quantité de tribut comprend trois types de marques à savoir : une marque d’individuation/substantialisation, une marque de classification et une marque de dénombrement/quantification. Ci-dessous divers tributs (couvertures de la p. 30).

Figure 19

Figures illustrant la variété des tributs et des types de couvertures dans la Matrícula de tributos

Les codex Vergara, Santa Maria Asunción [48], Otlazpan et autres sont des registres du XVI^e siècle contenant des informations démographiques et cadastrales sur les exploitants et sur les parcelles exploitées (Noriega, 1994). Ces sources confirment les témoignages sur le calcul de l’impôt de Cortès « celui qui les possède [les lots de terre] peut payer le tribut parce que pour chaque mesure tant d’impôt leur est attribué selon l’endroit où se trouvent les terres », ou de son fils « celui qui a un terrain paie un tribut, celui qui en a deux, deux […] ; et celui qui a une terre irriguée paie le double de celui qui a une terre sèche » (Harvey et Williams;1981).

Ces documents d’un genre particulier se rangent en trois types complémentaires : 1) tlacatlacuilolli [49], registre généalogique des personnes liées à l’exploitation des parcelles.

Figure 20

Codex de Santa Maria Asunción, folio 2r : tlacatlacuilolli ou registre généalogique des personnes de la famille de Pedro liées à l’exploitation d’une parcelle de terrain

Sur la figure ci-dessus, on voit : Pedro Tlacochquiauh, sa femme, leurs 2 enfants, le frère de Pedro avec sa femme et leur fils. Chaque adulte est figuré par une tête et son nom. Au décès de quelqu’un, l’administration noircit la tête qui le représentait.

2) milcocolli [50], registre des terres reproduisant le contour des parcelles, indiquant le type de sol, et donnant en chiffres de style trait/rond (et non de style point/barre) la longueur des côtés exprimée en nombre de quahuitl [51]. La numération du système tardif contenait aussi 5 signes désignant des fractions de l’unité de longueur : main, coeur, flèche, bras, os [52].
Voici l’enregistrement (folio 10r) de 4 champs dont 2 sont à Pedro et 2 à son frère :

Figure 21

Codex de Santa Maria Asunción, folio 10r : milcocolli ou enregistrement des dimensions des côtés de quatre parcelles de terrain dont 2 sont à Pedro et 2 à son frère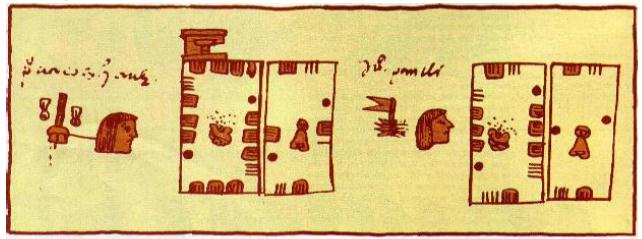

Sur le 1er côté du 1er rectangle, on voit : 1 rond, 3 groupes de cinq traits et 4 traits isolés [53]. Supposant qu’il s’agit d’un système additif et posant qu’un trait représente une unité et qu’un point en représente vingt, Harvey et Williams déchiffrent la longueur de ce premier côté : 20 + 5 + 5 + 5 + 1 + 1 + 1 + 1 = 39, et ainsi des autres longueurs inscrites sur chaque côté de chacune des 4 parcelles rectangulaires : (39, 15 + ‘main’, 39, 15) ; (25, 8, 26, 8) ; (38, 8, 39, 9) et (20, 8, 20, 9).

3) tlahuelmantli [54], registre qui reprend les parcelles du milcocolli sous forme de rectangles beaucoup plus ‘abstraits’ et dont certains présentent un petit décrochement en haut à droite.

Figure 22

Codex de Santa María Asunción, folio 19v : tlahuelmantli ou registre qui reprend les parcelles du milcocolli sous forme de rectangles ‘abstraits’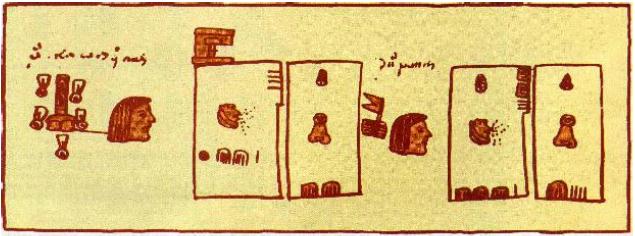

Chaque rectangle comprend des signes et des nombres déchiffrés dans les années quatre vingt par Harvey et Williams. Partant des témoignages anciens qui précisent que l’impôt était fonction de la quantité et de la qualité des terrains :

"un terrain paie un tribut, celui qui en a deux, deux […] ; et celui qui a une terre irriguée paie le double de celui qui a une terre sèche"

Harvey et Williams réalisèrent des expériences à partir de l’idée que les nombres inscrits dans le 3^ème registre (tlahuelmantli) devaient être reliés à ceux du 2^ème (milcocolli), et que le tout devait servir à déterminer l’impôt. Ils commencèrent par distinguer les zones de chaque texte et leur attribuer des significations conjecturales jusqu’à l’obtention d’une certaine cohérence interprétative. Ils distinguent ainsi une zone centrale, le registre Z, destinée à recevoir les signes indiquant la nature du terrain (Noriega, 1998:78-79).
Leur pierre de rosette fut l’idée que les trois zones du tlahuelmantli contenant des signes numériques devaient être considérées ensemble, comme le tout de l’expression complexe d’un nombre qui, selon la conjecture principale, devait à la fois traduire la surface du champ et être fonctionnellement reliées aux longueurs de ses côtés [55] connues par le milcocolli.
Après de multiples calculs et expériences de pensée, leur constat est qu’il s’agit de l’écriture d’un nombre, que ce nombre exprime la surface du champ et qu’il est bien corrélé aux longueurs des côtés du deuxième registre (dans 71% des cas, l’écart est inférieur à 10%).

Figure 23

Codex connu comme les ‘Papiers de l’ambassade américaine’ où un lien est explicitement marqué entre les données milcocolli (mesures des côtés) et les données tlahuelmantli (mesures des surfaces).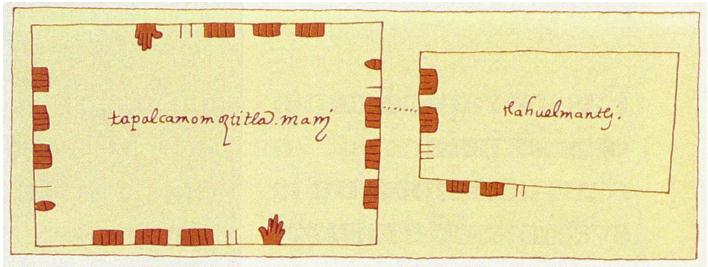

"Papeles de la Embajada Americana (…) Le champ de gauche fournit les données milcocoli et celui de droite (reliés par une ligne de points) les données tlahuelmantli. La superficie du champ peut être calculée à partir des données milcocoli en multipliant la longueur par la largeur, ce qui donne 272 quahuitl² (quahuitl est une unité de longueur, d'où quahuitl² pour l'unité de surface correspondante), chiffre que l’on trouve dans le champ de droite." (ibid.: 1081)

De fait, dans le champ de droite on lit les chiffres 13 et 12 interprétés comme constituants du nombre 13 × 20 + 12 = 272 ; et dans le champ de gauche on lit la largeur ‘16 et 1 os ( ?)’ et la longueur ‘17 et 1 main’ ; admettant que l’os et la main soient des fractions de l’unité, le produit des dimensions est compris entre 16 × 17 = 272 et 17 × 18 = 306, donc dans l’intervalle [272, 306] qui contient (de justesse) la surface 272.
La conclusion de Harvey et Williams est la thèse, nouvelle et revendiquée comme telle, d’une numération aztèque de position. Dans l’encart sur les ‘systèmes de numération positionnelle’ qui en donne des exemples et en explique le fonctionnement on lit :

"dans le système aztèque, on joue avec des traits et des points dont la valeur varie selon la position : 3 traits dans le premier registre signifie 3, mais trois traits dans le second registre signifient 3 x 20. Les points n’apparaissent que dans le troisième registre et ont pour valeur 20² ou 400 " (ibid.:1074)

Et plus clairement encore dans le corps de l’article :

"L’intérêt de notre récent déchiffrement de deux documents datant des premiers temps de la colonisation (…) est de nous fournir la première preuve directe que les Aztèques utilisaient aussi un système de numération de position et un symbole spécial pour zéro." (ibid.:1068)

Notre propos est triple : a) souligner l’importance des expérimentations arithmétiques réalisées par Harvey, Williams et les autres, b) valoriser le lien établi entre les longueurs milcocolli et les aires tlahuelmantli, et c) critiquer la conclusion que l’enregistrement des surfaces du tlahuelmantli s’est fait en numération de position avec zéro et non pas en numération additive traditionnelle comme celui des longueurs milcocolli.

5. Le "système de numération de Position de Texcoco"

"Le système de numération de position de Texcoco fonctionne de la façon suivante : dans le registre tlahuelmantli, les nombres sont inscrits selon trois positions que nous appelons « registres ». Le premier registre situé dans le décrochement représente les unités indiquées par des traits de 1 à 19. Chaque groupe de 5 traits est marqué par une ligne qui joint les traits à leur sommet. La valeur du registre va de 0 à 19 et, quand il s’agit de 0, le décrochement n’est pas dessiné ou laissé vide. La base du rectangle constitue le second registre qui représente 1 à 19 unités de 20 (soit de 20 à 380 dans notre système numérique). Le total des deux registres s’obtient en multipliant le chiffre du deuxième registre par 20 et en additionnant le résultat à celui du premier registre. Cette somme ne dépasse jamais 399. La partie centrale du rectangle est le troisième registre et représente les quantités de 400 et plus par des multiples de 20. Pour obtenir le total des premier et troisième registres, le chiffre du troisième est multiplié par 20 et ajouté à celui du premier. Le point [le rond] symbole de 20 n’intervient donc que dans le troisième registre et sa position lui confère la valeur de 20² soit 400 et non plus 20. [une phrase peu compréhensible : ‘les deuxième et troisième registres ne sont jamais figurés’]. Lorsqu’il n’y a aucun chiffre dans le troisième registre, l’épi de maïs est dessiné dans le haut du rectangle et signifie 0." (ibid.:1077 et 1079)

Commençons par remarquer que les longueurs milcocolli ne sont pas écrites en numération de position mais en numération traditionnelle : la numération aztèque de type additif. Certes, elle a subi un petit lifting : ses chiffres ne furent écrits ni dans le style répétitif de la numération aztèque traditionnelle ni dans le style point/trait de la numération maya, mais dans le style trait/rond du système que nous avons qualifié de tardif.
Regardons, registre par registre, l’écriture tlahuelmantli des surfaces des 4 champs de Pedro et de son frère avec les yeux recommandés par Harvey et Williams. Le 1^er registre, R₁, est le petit décrochement qui apparaît seulement sur certains rectangles (champs 1 et 3). Il reçoit les unités dont le nombre est indiqué par des traits, soit dans l’ordre des champs :

4 traits/pas de décrochement/13 traits/pas de décrochement

Le 2^ème registre, R₂, est la base du rectangle. A condition qu’il n’y ait pas de quatrecentaines (auquel cas on place un épi de maïs en haut dans le registre Z₃), le registre R₂ reçoit les vingtaines dont le nombre est indiqué par des traits, soit dans l’ordre des champs :

base vide/10 traits/16 traits/9 traits

Le 3^ème registre, R₃, est au centre du rectangle (sous le glyphe Z0 de la nature du champ). A condition qu’il y en ait (c’est le cas du champ 1), le registre R₃ reçoit les quatre-centaines dont le nombre est en écriture additive classique : il est enregistré comme la somme des ses vingtaines (dont le signe est un rond) et de ses unités (dont le signe est un trait) ; pour le champ 1 (seul exemple dans lequel R₃ n’est pas vide) on trouve :

1 rond et 11 traits.

On notera que les opérandes ne sont pas placés dans le même ordre : dans le milcocolli, ils sont rangés des unités vers les vingtaines (ordre croissant) ; dans le tlahuelmantli, ils sont en ordre décroissant. Soit le schéma récapitulatif (Tableau 7) du tlahuelmantli :

Tableau 7

Dans les Papeles de la Embajada Americana, l’écriture des aires est différente [56]. On ne voit pas de registre R₁ (décrochement). On ne voit pas de registre R₂ (des vingtaines, 20¹), mais un registre R₂’ des unités (dé)placé hors du rectangle en position symétrique des registres R₂. Ce registre R₂’ contient 12 traits (= 12 x 200). On ne voit pas de registre R₃ (des vingtaines et quatre-centaines, 20¹ et 20²) au centre du rectangle, mais un registre R₃’ (des vingtaines) sur le côté ouest intérieur du rectangle où sont inscrits 13 traits (= 13 × 20¹). Harvey et Williams nous disent que R₂’ et R₃’ contiennent l’écriture 13 × 20 + 12 = 272 de la surface. On note : a) il n’y a pas de quatre-centaines et b) il n’y a ni registre Z₃ ni épi de maïs. La règle « Lorsqu’il n’y a aucun chiffre dans le troisième registre, l’épi de maïs est dessiné dans le haut du rectangle et signifie 0 » est mise en défaut ou ne s’applique pas ici.

Figure 24

Papeles de la Embajada Americana

Reste à lire ces assemblages de signes placés dans les registres eux-mêmes placés en divers lieux du rectangle. Lire revient ici à trouver la valeur numérique de ces assemblages. Le critère adopté par Harvey et Williams repose sur une statistique des écarts entre :

a) la surface calculée comme produit de la longueur et de la largeur du milcocolli.
b) la surface obtenue en additionnant les valeurs des registres du tlahuelmantli.
Dans l’exemple des Papeles de la Embajada, nous avons observé plus haut que : a) l’aire obtenue comme produit des dimensions milcocolli est comprise entre 272 et 306 donc dans une fourchette que l’on peut noter IC (Intervalle Calculé), et b) l’aire obtenue par addition des registres tlahuelmantli a la valeur 272 que l’on peut noter SI (Surface Indiquée) et admettre son appartenance à l’intervalle [272, 306]. Appliquée aux 4 champs tlahuelmantli, la lecture donne les valeurs SI et IC suivantes :

Tableau 8

	Champ 1	Champ 2	Champ 3	Champ 4
Z₃		maïs (zéro)	maïs (zéro)	maïs (zéro)
R₃	1×20²+11×20¹=620
R₂		10×20¹=200	16×20¹=320	9×20¹
R₁	4×20⁰		13×20⁰
SI	624	200	333	180

Les champs du milcocolli ne sont pas parfaitement rectangulaires, et peuvent avoir jusqu’à deux longueurs et deux largeurs différentes. Plutôt que de choisir arbitrairement l’une ou l’autre pour calculer la surface, on calcule les extrema du produit [57] qui fournissent les bornes de l’Intervalle Calculé. On peut alors constater que l’interprétation construite par Harvey et Williams est fort satisfaisante [58] :

Tableau 9

	Champ 1	Champ 2	Champ 3	Champ 4
Min l×L	15×39=585	8×25=200	8×38=304	8×20=160
Max l×L	(15+m)×39=608,4 [59]	8×26=208	9×39=351	9×20=180
IC	[585,608]	[200,208]	[304,351]	[160,180]
SI	624	200	333	180
SI ∈ IC ?	NON	OUI (limite inférieure)	OUI	OUI (limite supérieure)

6. Pourquoi la "numération de Texoco" n'est pas une numération de position

La conceptualisation polynomiale et la sémiotisation des nombres en numération de type positionnel font jouer à la position des chiffres dans l’écriture le rôle de signifié des nœuds (puissances de la base). Cette absolue systématicité invite le scribe à prolonger sans limite la suite des positions, et elle lui offre ainsi la capacité de créer et d’écrire des nombres aussi grands qu’il veut [60]. De plus, les positions sont exclusives : chacune ne reçoit que le chiffre qui marque le coefficient multiplicatif du nœud attribué à cette position. La « numération de Texcoco » ne vérifie pas ces propriétés. D’abord parce qu’il y a seulement 4 positions d’écriture prédéfinies, les registres R₁, R₂, R₃ et Z₃. Ensuite parce que ces 4 registres ne reçoivent que les coefficients de 3 nœuds, ceux des monômes en 20⁰, 20¹ et 20². Le registre Z₃ est en effet une sorte de double partiel et inutile de R₃. Tous deux reçoivent des coefficients de 20² . Mais pas les mêmes. Quand il n’est pas vide, le registre R₃ reçoit le coefficient de 20², c’est-à-dire l’un des 19 chiffres non nuls ; au contraire, Z₃ reçoit seulement l’épi de maïs « lorsqu’il n’y a aucun chiffre dans le troisième registre [R₃]». La « numération de Texcoco » est ainsi limitée aux nombres inférieurs à 8 000. C’est 20 fois moins que la capacité générative de la numération additive traditionnelle (160 000). Mais il est surtout impossible de faire de l’épi un symbole du zéro de position [61]. Harvey et Williams en firent donc un curieux zéro qui n’apparaît qu’en position initiale et qui ne sert qu’à signifier « 0 x 20² ».

Pour l’ordre de lecture/écriture, les positions viennent habituellement les unes à la suite des autres, de manière à former une file [62] de chiffres qui commence toujours avec celui du nœud des unités, celui de 20⁰. En « numération de Texcoco » le registre R₁ des unités (petit décrochement) n’existe pas toujours, car le scribe le dessine seulement quand le coefficient des unités n’est pas nul et que la surface s’écrit au moins sur deux registres, c’est-à-dire quand R₃ ou R₂ n’est pas vide (la surface dépasse 400 ou elle dépasse 20). En d’autres termes quand R₁ est dessiné, il forme une file avec R₂ ou (exclusif) avec R₃. Dans le premier cas, la surface est un nombre à deux chiffres, c₀ c₁, tous écrits en traits, comme dans l’exemple du champ 3 : on transcrit 16.13. et on lit 16.13. = 16 × 20¹ + 13 × 20⁰ = 333. Mis à part l’éloignement visuel des registres R₁ et R₂, la notation fonctionnerait comme une numération de position limitée à l’écriture des nombres à deux chiffres de la forme c₀ × 20⁰ + c₁ × 20¹. Dans le second cas, la surface est un nombre à trois chiffres (R₃ contient les coefficients de deux nœuds, 20¹ et 20²) comme dans l’exemple du champ 1 : on transcrit 1.11.4. et on lit [1.11.]4. [63] = [1 × 20¹ + 11 x 20⁰] × 20¹ + 4 × 20⁰ = 624. A l’intérieur de R₃, en effet, ce n’est pas la position qui définit la valeur du nœud, mais le changement de symbole : le rond réfère à la vingtaine et le trait réfère à l’unité. Ce qui montre que R₃ contient un nombre en numération additive traditionnelle, à savoir le nombre 31. Il détermine des vingtaines. C’est le premier opérande, 31 × 20, de la surface. Le second opérande est le contenu 4 (en numération traditionnelle) du registre R₁. En raison de ces différentes observations, nous suggérons de ne pas considérer le « système de Texcoco » comme une numération de position avec zéro [64].

7. Nouveauté du "système de Texcoco"

7.1 Arrangements typographiques des chiffres : alignés ou distribués en registres

Si le système tardif de Texcoco n’est pas une numération écrite du type Position, de quel type est-il et à qui servait-il ? Un premier élément de réponse. Lorsqu’il s’agit d’enregistrer les longueurs des côtés dans le milcocolli, le système tardif est un décalque de la numération additive traditionnelle [65] : leurs signes ont le même signifié et la même fonction. Seuls leurs signifiants sont différents : trait/rond dans le système tardif, et point/drapeau dans la numération aztèque traditionnelle. Le changement ne va pas plus loin, et n’affecte pas par exemple le caractère vigésimal de la numération. D’ailleurs, il n’y a pas de places de registres différenciés : la mesure d’un côté est inscrite sur le côté du rectangle dont elle donne la longueur sous forme d’un entier (à un ou deux chiffres) écrit en numération additive traditionnelle. C’est comme dans la notation des tributs ou celle du nombre des victimes : un nombre (à un ou plusieurs chiffres) est associé à un classificateur (pas toujours sous-entendu) et à un objet (toujours dessiné, souvent avec beaucoup de détails qui peuvent parfois être numériques).
La numération utilisée pour écrire les surfaces dans le tlahuelmantli est-elle similaire à la numération utilisée pour enregistrer les longueurs dans le milcocolli ? Oui, en ce qui concerne les signifiants des signes : longueurs et surfaces sont enregistrées à l’aide des chiffres trait/rond, et en négligeant le fait de l’usage de signes pour les fractions de l’unité de longueur.
Non, en ce qui concerne l’emplacement des opérandes d’un nombre à plusieurs monômes. Dans le milcocolli, les opérandes sont concaténés dans un seul registre. Par contre, dans le tlahuelmantli, ils sont distribués dans des registres différents. De plus, la correspondance entre les places de registres (R₁, R₂, R₃, Z₃) et la valeur numérique des nœuds (20⁰, 20¹, 20²) n’est pas biunivoque. Cela suffit à réfuter la thèse que la numération tlahuelmantli de Texcoco serait du type Position. Cela montre aussi que la numération tlahuelmantli n’est pas identique à la numération milcocolli, car, sans jouer le rôle de la position en numération de position, la place des registres est partiellement pertinente dans le tlahuelmantli :

a) dans le registre R₃, l’opposition unité/vingtaine n’est pas marquée par la position, mais par l’opposition trait/rond (par un changement de symbole)
b) dans R₃, un nombre à deux chiffres désigne des vingtaines,
c) dans R₁ ou dans R₂, un nombre à un chiffre désigne des unités.

Du point de vue de l’épistémologue, deux habitus s’affrontent : i) écrire les chiffres (ou les opérandes) d’un nombre (qui en possède au moins deux) les uns à la suite des autres dans l’espace d’un seul et même registre, et ii) les écrire en les distribuant dans des registres différents. Dans le système milcocolli, les chiffres sont en file dans un seul registre. Dans le système tlahuelmantli, ils sont distribués sur quatre registres.
C’est la plus profonde différence entre les deux systèmes tardifs de numération.

7.2 Nature et limite de la nouveauté du système de Texcoco

Nous avons réfuté l’hypothèse que cette différence marquerait le passage du type additif au type positionnel. D’où la question : Que marque-t-elle ? Notre thèse est que l’ordre de succession des registres en numération tlahuelmantli de Texcoco est lié à des contraintes de mise en page [66] que les Aztèques auraient eu intérêt à emprunter aux Espagnols (pour un autre exemple, voir Encart 1) . Comme un grand nombre de peuples, les Aztèques comptaient, mesuraient, pesaient… Mais les étalons et les mesures étaient nombreux, hétéroclites et incommensurables entre eux. Les mesures (longueur notamment) s’exprimaient habituellement par des nombres ‘complexes’ comme nos semaines divisées en 7 jours, divisés en 24 heures, divisées en 60 minutes. Un notaire, même de nos jours et après l’imposition du système métrique, inscrit par exemple la surface des terrains en hectares, ares et centiares, et, dans le même acte, la surface des pièces habitables en mètres carrés.
Quand le système des mesures est très familier ou quand il est très systématique, les usagers peuvent, sans trop d’inconvénients, ne pas écrire explicitement la valeur des différents nœuds. Car la familiarité, dans un cas, ou la systématicité, dans l’autre, permet aux familiers du système de restituer ces informations laissées sous-entendues. Notre notaire pourrait écrire : soit (dans l’ordre ou le désordre) « 12 hectares 34 ares 45 centiares », soit (nécessairement dans l’ordre) « 12/34/56 (sans unités) ».
Avant la diffusion du système métrique, les calculs se faisaient (péniblement) sur des nombres complexes ; ce qui conduit i) à choisir les étalons et les rapports d’unités de manière à ne manipuler que des mesures d’une complexité réduite, des nombres à peu de chiffres significatifs, et ii) à traiter séparément les quantités de différents nœuds : les hectares avec les hectares, les ares avec les ares…
Appelons ‘hygiène typographique’ cet habitus qui a parfois conduit à développer des outils spécialisés comme les bouliers, abaques et autres planches à poussière. Il peut conduire aussi à distribuer les opérandes dans les colonnes d’un tableau (réel ou imaginé).
A l’époque du milcocolli, dans le contexte des revendications du 16^ème siècle opposant un parti indigène à un parti espagnol sur la question de la valeur des tributs imposés, le parti indigène avait, plus que le parti espagnol, avantage à connaître et utiliser les modes de conceptualisation et de sémiotisation de l’autre. A s’approprier les moyens de vérifier le calcul de l’impôt foncier, de déterminer les surfaces, de les calculer en fonction des côtés [67].
Or les Européens et leurs alliés – par ex. les encomenderos, les notaires et les rédacteurs indigènes des rubriques en nahuatl ou espagnol qui émaillent les codex coloniaux – utilisaient des nombres complexes (par exemple une surface de 3 perches et 17 pieds carrés) [68] pour deux raisons principales : la numération de position était moins diffusée que la numération romaine, et, surtout, la Révolution française n’avait pas encore inventé et imposé le système métrique des poids et mesures.
Dans l’ancienne métrologie européenne, les unités de surface des champs (terre travaillée) portaient des noms qui renvoient i) au labeur agricole et aux rendements du travailleur et/ou du sol [69], et ii) à une multitude [70] de quantités adaptées aux coutumes et besoins locaux ; d’où le paradoxe d’une multiplicité de mesures agraires incommensurables et souvent redéfinies au niveau des provinces ou de l’état [71], qui contraste au niveau des petites localités avec l’usage stable d’un petit nombre de mesures familières et simples, quantifiées par un petit coefficient multiplicatif le plus souvent écrits en chiffres romains.

En d’autres termes, les Aztèques furent confrontés, d’une part, aux idées d’une population rurale européenne qui tenait pour fondateurs les liens et rapports entre le travail humain et une « mère nature » vue comme terre travaillée assurant des rendements comptabilisables, et, d’autre part, non pas aux savoirs arithmétiques des savants de l’époque allant de Chuquet (1484) à Stevin (1586), mais aux habitus des agents de l’administration avec qui il fallait traiter des conflits entre propriétaires indigènes et encomendero. Les protagonistes sont connus, ce sont les dépositaires des anciens titres indigènes de propriété, les notaires, les avocats, les juges...
En matière d’écriture des surfaces, les règles de l’hygiène typographique sont suivies par l’administration et les gens de culture occidentale : ils séparent les opérandes et les placent dans les colonnes d’un tableau (réel ou pensé) ; par ailleurs, ils évaluent rendements et productions agricoles en fonction des dimensions du terrain et en tenant compte des qualités du travailleur et de la terre.
Disposer du savoir implicite enfoui dans ces habitus permet aux accusateurs de développer des arguments quantitatifs pour déjouer les fausses déclarations. Et il permet aux accusés de développer d’autres arguments quantitatifs pour démontrer leur bonne foi ou dénoncer les excès de l’encomendero.

Figure 33

Codex Kingsborough : figure de l’encomendero illustrant les rapports sociaux ente encomendero et indigènes

Ce qui conduit à la conjecture que les Aztèques adoptèrent deux habitus a priori espagnols : a) distinguer les opérandes et les placer dans des registres typographiquement disposés selon des règles nouvelles (empruntées ou métissées) développées par l’usage occidental de l’abaque et des tableaux, et peut-être aussi b) évaluer les surfaces par un calcul (largeur x longueur).
Les données du codex Santa Maria de Asunción s’expliquent en tout cas plus simplement dans le cadre de cette conjecture que dans celui de l’invention aztèque d’une numération de position avec zéro [72]. La conjecture évite par exemple de faire dire à l’épi de maïs qu’il est symbole du chiffre zéro, alors que sa présence est plus vraisemblablement un signal permettant de classer rapidement les fiches en deux paquets distincts : la classe des contribuables dont l’exploitation atteint ou dépasse le seuil 400, et celle des contribuables dont l’exploitation est inférieure à ce seuil.
La classe des petits contribuables est sur-caractérisée : a) pas de quatre-centaines, b) la place du nœud 400 dans le registre R₃ reste vide (tellement vide que les vingtaines sont alors placées non dans R₃ mais dans R₂) et c) l’inscription du signe ‘épi de maïs’ dans le registre Z₃ (inutile parce a) et b) sont déjà deux façons d’écrire le monôme 0 × 20²).

Selon moi, l’intérêt de l’épi de maïs est de faire voir, comme un nez rouge au milieu de la figure du clown, qu’il s’agit d’un champ de surface inférieure au seuil 400, donc le lopin d’un petit propriétaire qui risque de crouler sous les dettes et de subir de plein fouet les brimades de l’encomendero.
Dans le contexte colonial mésoaméricain, les interactions indiens/métisses/espagnols furent intenses et précoces [73], notamment dans l’espace judiciaire qui servait de creuset à l’apparition de nouvelles formes d’écritures et de rhétoriques. Ramenée à ce qu’elle fut – changement des signifiants [74] et redistribution de l’espace typographique où inscrire les opérandes d’une surface –, il est possible de préciser en creux ce que ne fut pas le système tardif d’écriture des nombres tlahuelmantli.
La nouveauté à l’époque coloniale de la notation numérique dite « système de Texcoco » ou « système tardif » n’était pas encore le début de l’abandon des numérations aztèques traditionnelles additives ; ni l’annonce du renouveau d’une numération mésoaméricaine et vigésimale de position, ni même encore l’emprunt par les Aztèques de la numération européenne décimale de position que le colonisateur espagnol finirait par imposer.

Un mot de conclusion

Considérée en son noyau R+D, Recherche et Développement, la production intellectuelle d’un peuple ou d’une culture prend des formes et génère des applications différentes selon les organisations où elle se réalise. D’après Posner (1983:53) cité par Cauty (1987:257- 258), des contraintes systémiques générales poussent les sociétés à trouver un compromis équilibrant économie de performance et économie du système, car le bénéfice de la réduction des expressions (clef de l’économie de performance) est consécutif et fonction de l’investissement nécessaire à l’obtention d’un système plus sophistiqué sans lequel les expressions ne seraient ni simplifiées ni simplifiables.
Dans le domaine d’expérience ‘nombres/numérations’, le type positionnel maximalise l’économie de performance ; mais pour en disposer et pouvoir en maîtriser les ressources, la société doit instituer la transmission de ce système complexe et difficile à acquérir, et faire passer au moins certains individus par des années d’apprentissage :

"[...] il est en tout cas historiquement constaté que le chemin menant vers une plus grande économie de performance s’est poursuivi au détriment de l’économie du système [...]"

Posner donne l’exemple de la Chine ancienne :

"Ils [chinois] ont épargné à leurs scribes une dépense intellectuelle dans l’exercice quotidien de leur profession, mais ce faisant ils ont élevé le coût intellectuel de la formation professionnelle [...]"

et montre l’importance du type d’organisation que la société s’est donnée :

"une société de la division du travail qui s’autoriserait une caste de scribes hautement spécialisés, se sera volontiers accommodée du prolongement de leur formation, si, de ce fait, l’efficacité des affaires quotidiennes a pu être augmentée. Une société égalitaire qui ambitionne une formation aussi vaste que possible pour le plus de gens possible, s’accommodera par contre d’une moindre efficacité dans certains domaines particuliers de la vie professionnelle, si cela peut libérer les capacités d’apprentissage pour d’autres domaines."

Les Mayas, jusqu’au postclassique où tout allait se perdre, ont produit une arithmétique de qualité et une élite de scribes formés pour en créer les outils et les utiliser. Ils inventèrent deux zéros, une numération de position et un système d’unités de temps ; ils développèrent le calcul en arithmétique modulaire et l’appliquèrent à la production de calendriers et d’éphémérides précis au jour près.
L’invention d’une numération de position est un événement rare. Mais une fois inventée, sa diffusion est irréversible, et dans ce mouvement, à l’échelle planétaire, c’est la numération décimale de l’Inde qui s’est taillé la part du lion. Donc, si l’on acceptait de créditer les Aztèques de l’usage d’une numération de position, la prudence épistémologique consiste à étudier les circonstances de ce petit miracle et chercher a priori du côté de la diffusion de cette belle invention depuis l’une des deux régions de l’espace/temps qui possédaient déjà ces savoirs mathématiques : le monde voisin des Mayas et le monde omniprésent du colonisateur espagnol. Comme on le sait, la source maya n’avait plus, à l’époque coloniale, la splendeur de l’époque classique, l’intelligence arithmétique maya ne brillait plus, et se mourrait dans de rares lieux confinés de la mémoire. Ce qui réduit le champ à explorer.
Les Aztèques ont produit des outils comptables et une armée d’administratifs qualifiés pour lever l’impôt. Ils inventèrent l’agriculture sur jardin flottant (chinampo) et développèrent. la gestion des cités sous contrôle de la Triple alliance avant de se voir contraints par l’Histoire de tout subordonner aux exigences étrangères des Espagnols qui avaient établi le nouveau régime de l’encomienda. Ils métissèrent leur numération traditionnelle, apprirent l’espagnol, l’alphabet et le calcul. Ils apprirent à calculer les surfaces et adoptèrent les règles du bien écrire des notaires qui placent les opérandes dans des colonnes ou registres bien séparés.
Il n’y avait pas de mathématiciens mayas dans le monde du tribunal où les Aztèques produisaient comme preuves et argumentaires les tlahuelmantli. Par suite les Aztèques ne pouvaient être exposés qu’à une seule numération de position, celle du colonisateur. Une numération savante de position, forcément ambiguë. A la fois objet de rejet, car symbole de l’oppression subie, et objet de désir, car outil arithmétique aux performances inégalées. Qu’on la dise « arithmétique aztèque » (Harley et Williams) ou « proto-géométrie aztèque » (Williams et Jorge), la nouveauté apparue dans les codex du bassin de Mexico est pour nous la fille métisse du couple colonisation/résistance, une fille parée d’habits traditionnels et d’habits d’emprunts. Un peu plus à chaque génération, selon un gradient qui voit les Aztèques passer à la décimalité, aux chiffres arabes… jusqu’à l’abandon prévisible de la numération additive traditionnelle et l’adoption de la numération de position du conquérant espagnol… Bilingue ou non, l’école de la vie et l’école tout court s’y emploient chaque fois plus efficacement.
Puisse cet article contribuer à la sauvegarde des vestiges encore vivants de deux espèces cognitives quasiment disparues : les traces de la numération positionnelle des Mayas du classique et celles de la numération additive des Aztèques de la Triple Alliance.

Bibliographie

Beltrán (de Santa Rosa), P., 1859, Arte del idioma maya reducido a sucintas reglas, y semilexicon yucateco, Mérida (Mexique), Imprenta de J.D. Espinosa (1742/1746).

Castillo, V., 1972, ‘Unidades nahuas de medida’, Estudios de Cultura Náhuatl, n° 10, México [un extrait dans Arqueologia Mexicana édition spéciale La Matrícula de tributos].

Cauty, A., 1984, ‘Taxinomie, syntaxe et économie des numérations parlées’, Amerindia, n° 9, Paris, Association d’Ethnolinguistique Amérindienne

Cauty, A., 1987, L’énoncé mathématique et les numérations parlées, Thèse de doctorat d’Etat ès sciences, Université de Nantes.

Cauty, A., 2010, Kit du randonneur en calendrier maya, CultureMATH, document pdf (6,46 Mo, 36p.)

Cauty, A. et Hoppan, J.-M., 2002, ‘Des spécificités des numérations mayas précolom biennes', Mémoires de la Société de Linguistique de Paris, nouvelle série, tome XII, Leuven : Perters, pp. 121-147.

Cauty, A. et Hoppa, J.-M., 2007, ‘L'écriture maya des nombres’ en ligne sur CultureMath.

Durand-Forest, J., Dehouve, D., Roulet, E., 1999, Parlons nahualt : la langue des aztèques, Paris, L’Harmattan, 346 p.

Duverger, C., La Méso-Amérique, Flammarion, 1999, 478 p.

Guitel, G., 1975, Histoire comparée des numérations écrites, Paris : Flammarion.

Harvey, H.R. et Williams, B, 1981, ‘L’arithmétique aztèque’, La Recherche, n°126, Paris, pp. 1068-1081.

Johan, P., 1995, ‘Opérons en toises, pieds, pouces’ Repères-Irem, n° 18, janvier 1995, p .35-42.

Launay, M., 1986, Catégories et opérations dans la grammaire nahuatl, Thèse de Doctorat d'Etat, Université de Paris Sorbonne.

Lesbre, P., 2008, ¿Influencias occidentales en el "Mapa Quinatzin"?, Revista Española de Antropología Americana, Vol. 38, n° 2, p. 173-197.

Marcus, J., 1992, Mesoamerican Writing Systems, Propaganda, Myth, and History in Four Ancient Civilizations, Princeton Univ. Press, Princeton, NJ.

Meluzin, S. 1987, The Tuxtla Statuette: An Internal Analysis of Its Writing System in The Periphery of the South-eastern Classic Maya. Latin American Studies, vol. 61, p. 67-113.

Noriega, P. 1994, ‘El Códice de Santa María Asunción. Un ejemplo de Sistema Catastral de Origen Prehispánico en el Valle de México’, Arqueología Mexicana Vol II, N.8, p. 74-96.

Pohl, M., Pope, K., Nagy (von), C., 2002, ‘Olmec Origins of Mesoamerican Writing’ Science, 6 Dec 2002; 298: 1984-1987.

Posner, R., 1983, ‘Les nombres et leurs signes. Histoire et économie de la représentation des nombres’,Revue de linguistique du DRLAV, Paris : Centre de Recherche de l’université Paris 8.

Queixalos, F., 1986, Autobiographie d’une néonumération, Amerindia, n° 11, Paris : Association d’Ethnolinguistique Amérindienne.

Sepulveda y Herrera, M.-T., sd, ‘Medidas, numerales y unidades para tributación’, La Matrícula de Tributos, Arqueologia mexicana , serie códices, p. 12-13.

Thouvenot, M., 1998, ‘Valeurs phoniques et unités de langue dans les glyphes des Codex Xolotl et Vergara’, Amerindia, n° 23, Paris : Association d’Ethnolinguistique Amérindienne, p. 67-97.

Urcid, J., 2001, Zapotec hieroglyphic writing, Studies in Pre-Columbian Art and Archaeology, 34, Dumbarton Oaks Research Library and Collection, Washington, D.C., 487 p.

Williams, B., et Jorge, M. del C., 2001, ‘Surface area comptutation in ancient mexico documentary evidence of acolhua. Aztec proto-geometry’, Symmetry : Culture and Science, Vol 12, n°1-2, page 185-200 http://www.ethnomath.org/resources/williams2001.pdf.

Approche critique comparée des nombres aztèques et mayas