Plan de Moulton dynamique

CultureMATH
accueil - contact

Géométrie non arguésienne dynamique

implémentée avec CaRMetal

Yves Martin - IREM de La Réunion

« [...] deux figures sont égales quand on peut les superposer ; pour les superposer il faut déplacer l'une d'elles jusqu'à ce qu'elle coïncide avec l'autre, mais comment faut-il la déplacer ? Si nous le demandions, on nous répondrait sans doute qu'on doit le faire sans la déformer à la façon d'un solide invariable. Le cercle vicieux serait alors évident. [É]
Cependant toute imparfaite qu'elle soit, cette définition implique un axiome. La possibilité du mouvement d'une figure invariable n'est pas une vérité évidente par elle-même, ou du moins elle ne l'est qu'à la façon du postulatum d'Euclide et non comme le serait un jugement analytique a priori. D'ailleurs en étudiant les définitions et les démonstrations de la géométrie, on voit qu'on est obligé d'admettre, sans les démontrer, non seulement la possibilité de ce mouvement, mais encore quelques-unes de ses propriétés. »

Poincaré, La Science et l'hypothèse (1902)

Historiquement, l'utilisation du mouvement dans les démonstrations de géométrie a toujours posé problème ; depuis Euclide, qui n'y recourt qu'une fois au tout début de ses Éléments, en passant par Proclus qui le dénonce, puis les différentes écoles arabes du IX^e au XII^e siècle, certains mathématiciens l'utilisant (al-Haytam), d'autres le refusant (al-Kayyam), jusqu'à Wallis qui l'utilise encore explicitement, le mouvement en géométrie traduit bien l'ambiguïté de la relation entre le monde sensible, sa modélisation, puis - pour les mathématiques - son axiomatisation.

C'est, en particulier, pour résoudre ce « cercle vicieux » comme le dit Poincaré ci-dessus, que David Hilbert, dans ses Fondements de la géométrie, axiomatise les propriétés attendues du mouvement en introduisant des axiomes minimaux de congruence de segments et d'angles.

Parmi les résultats les plus remarquables de son ouvrage, nous allons nous intéresser ici à l'importance du théorème de Desargues pour construire la géométrie euclidienne. Une géométrie qui vérifierait les autres propriétés usuelles attendues, à l'exception du théorème de Desargues, serait assez surprenante par rapport à notre environnement euclidien immédiat, et même, relativement à une éventuelle culture non euclidienne, qu'elle soit hyperbolique ou elliptique. Hilbert a qualifié de « non arguésienne » une telle géométrie, dans laquelle le théorème de Desargues n'est pas vérifié.

Comme nous allons le voir, cette géométrie ne vérifie pas les plus simples de nos représentations géométriques comme les cas d'égalités des triangles. En effet, nous allons nous trouver au sein d'une géométrie affine dans laquelle il n'y a pas de translation, ou si l'on préfère, avec des translations ne conservant pas les segments. Ainsi, le mouvement le plus élémentaire pour superposer des objets ne conserve pas les grandeurs géométriques de ces objets.

Autrement dit, avec la géométrie non arguésienne, on dispose d'un exemple de géométrie dans laquelle le mouvement n'est pas pertinent pour illustrer la congruence. C'est donc un exemple de géométrie qui illustre parfaitement bien les différents questionnements que l'utilisation du mouvement a pu soulever dans la pratique géométrique.

Pour illustrer cela - et ce n'est pas un paradoxe - nous allons utiliser la géométrie dynamique, sa manipulation directe, l'action sur les figures et donc le mouvement.

Après un travail systématique de Ruth Moufang, dans les années 1931-1933 axé sur les fondements, dans un contexte projectif la géométrie non arguésienne n'a jamais été beaucoup étudiée, en particulier parce qu'elle ne se prête pas au calcul algébrique et que chaque situation contient systématiquement de nombreux sous-cas. Elle n'a jamais été implémentée en géométrie dynamique car, jusqu'à ces dernières années, les logiciels n'offraient pas encore les outils permettant une implémentation aisée du modèle le plus simple connu : le plan de Moulton.

La situation a changé, en particulier avec le logiciel CaRMetal qui va nous permettre d'étudier la géométrie du plan de Moulton d'une manière nouvelle.

Ce travail pourra servir en formation initiale - ou continue - et montrer, à l'occasion de compléments de géométrie ou de l'utilisation d'un logiciel, l'importance de l'invariance des grandeurs par un déplacement dans notre modélisation géométrique, notamment en quoi, dans un contexte affine, cette invariance est liée à la propriété de Desargues.

Cett article contient plus de 20 figures qui nécessitent un premier applet java de 1,8 Mo. La page peut être un peu longue à charger. Il se peut qu'il faille la recharger pour disposer effectivement toutes de les figures fonctionnelles.

Pour la suite de cette présentation, il peut être utile de se rappeler la présentation axiomatique de Hilbert telle qu'elle sapparaît dans ses Fondements à partir de la 7^e édition. Elle se présente sous la forme de cinq groupes d'axiomes : les axiomes d'incidence, les axiomes d'ordre, les axiomes de congruence, l'axiome des parallèles et les axiomes de continuité. À partir des deux premiers groupes on peut définir les demi-droites et les segments.
Des axiomes d'ordre on retiendra en particulier celui dit « de Pasch » qui fut l'un des premiers manquements majeurs repérés par Pasch chez Euclide.

II.4. Si une droite du plan ne passe par aucun des sommets d'un triangle et rencontre un des côtés, alors elle rencontre l'un des deux autres côtés.

Vient alors le groupe des axiomes de congruence :

Définition : Entre les segments, il existe certaines relations exprimées par les mots congruent ou égal.

III.1. Sur une droite donnée et d'un côté d'un point A donné, il existe un point B tel que le segment AB soit congruent à un segment donné.

III.2. Si deux segments sont congruents à un même troisième, ils sont congruents entre eux.

III.3. Si B est entre A et C, si B' est entre A' et C', si AB et A'B' sont congruents et si BC et B'C' sont congruents, alors AC et A'C' sont congruents.

Le premier axiome introduit la possibilité de report d'un segment (l'unicité de B sera montrée), le deuxième aboutit à ce que la congruence des segments soit une relation d'équivalence et le troisième à la possibilité d'additionner les segments. Le report d'angles se traite de la même façon. Toutefois, l'unicité de l'angle doit être demandée axiomatiquement, alors qu'elle est démontrée pour les segments, justement par les angles, comme première conséquence de III.4 et III.5 ci-dessous. Par leur définition, les angles sont non concaves et non plats

III.4. Dans un plan donné, et d'un côté d'une demi-droite h donnée, il existe une unique demi-droite k telle que l'angle (h, k) soit congruent à un angle donné.

III.5. Si dans deux triangles ABC et A'B'C', on a les congruences entre les segments AB et A'B', entre les segments AC et A'C' et entre les angles BAC et B'A'C', alors on a aussi la congruence entre les angles ABC et A'B'C'.

Hilbert reprend l'exposé d'Euclide : il définit alors l'angle supplémentaire et l'angle droit comme égal à son supplémentaire. Il montre l'existence des angles droits et leur congruence (comme Proclus) ainsi que les trois cas d'égalité des triangles. Les derniers théorèmes avant l'axiome des parallèles portent sur la possibilité de bissecter un segment et un angle (avant d'étendre la notion de congruence aux figures planes ou de l'espace).

1. Desargues et Hilbert

Dans le cadre affine, le théorème de Desargues exprime simplement l'existence du groupe des homothéties-translations :

Soient ABC et A'B'C' deux triangles tels que (AB) // (A'B'), (AC) // (A'C') et (BC) // (B'C') alors les droites (AA'), (BB') et (CC') sont parallèles ou concourantes.

Avec la réciproque suivante : Si (AB) // (A'B'), (AC) // (A'C') et si les trois droites (AA'), (BB'), (CC') sont concourantes ou parallèles, alors (BC) // (B'C').

En fait la propriété est projective :

Si les six droites (AB), (AC), (BC) et (A'B'), (A'C') et (B'C') sont telles que (AA'), (BB') et (CC') sont concourantes, alors les intersections des droites (AB) et (A'B'), (AC) et (A'C'), (BC) et (B'C') sont alignées.

On se souvient aussi de la lecture affine de ce dernier théorème dans le contexte d'un plongement du plan dans un espace affine : cette propriété est une conséquence de l'existence des plans affines dans un espace de dimension 3.
Ci-dessous, un tétraèdre IABC est coupé par un plan (A'B'C'). L'alignement des points du théorème précédent résulte simplement de l'intersection du plan (ABC) avec le plan (A'B'C') ; en géométrie affine, cette intersection est une droite.

Dès la première édition de son ouvrage Les fondements de la géométrie (1899), David Hilbert discute longuement l'importance axiomatique du théorème de Desargues avec les résultats suivants :

Le théorème de Desargues ne découle pas des axiomes d'incidence (et d'ordre) de la géométrie affine plane.

Mais il découle de l'existence de l'espace affine

Pour la géométrie plane la preuve du théorème de Desargues nécessite les axiomes de congruence sur les angles, et plus précisément l'axiome qui lie la congruence sur les segments à celle sur les angles.

Ensuite Hilbert aborde l'importance de ce théorème pour la construction des nombres. Il obtient alors, dans le contexte de son axiomatique, les résultats suivants:

Sans le théorème de Desargues

Avec le théorème de Desargues

Il n'y a pas de possibilité de construire des coordonnées.

La multiplication des nombres n'est pas associative.

Sans la congruence, il est possible de construire une géométrie des coordonnées.

Une géométrie plane peut toujours être considérée comme une partie d'une géométrie de l'espace vérifiant les axiomes affines.

2. Plan de Moulton

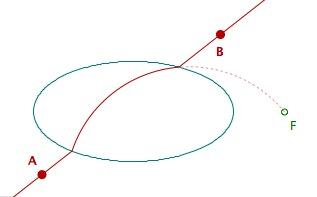
Lors de la première édition des Fondements de la géométrie, Hilbert a donné un exemple de géométrie non arguésienne, essentiellement pour en montrer l'existence : les droites sont celles du plan usuel sauf quand elles coupent une ellipse précise, la partie de la droite intérieure à l'ellipse étant remplacée par un arc de cercle bien déterminé (illustration statique ci-contre, plus de précisions dans l'édition critique de Paul Rossier, à la page 126).

Hilbert montre que les axiomes de congruences III.1 à III.4 sont vérifiés mais que le théorème de Desargues - qui se montre avec l'axiome III.5 - ne l'est pas comme on le voit ci-contre :

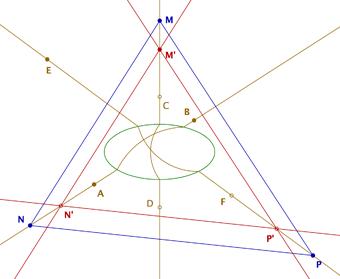
Les triangles MNP et M'N'P' ont leurs côtés parallèles (les droites affines usuelles correspondantes sont concourantes) alors que les droites de Hilbert (MM'), (NN') et (PP') ne sont pas concourantes.

Mais dès 1902, l'astronome américain Forest Ray Moulton (1872 - 1952) a proposé un exemple plus simple qui a ensuite été repris par Hilbert à partir de la 7^e édition de son ouvrage.

Dans l'exemple original de Moulton, la réfraction des droites était réalisée sur l'axe des abscisses, comme cela a été repris par Hilbert. Depuis, les mathématiciens qui ont travaillé sur le plan de Moulton ont généralement préféré faire basculer cette réfraction (qui pouvait avoir une connotation physique chez l'auteur) sur l'axe des ordonnées, ce qui permet une écriture plus simple de la situation. Mon travail s'inscrit dans cette tradition.

Les points du plan de Moulton sont les points du plan usuel RxR. Les droites sont les droites usuelles (y compris les droites d'équation y = m) à l'exception de celles de pente négative : dans ce cas la droite de Moulton est une droite affine par morceaux telle que la pente de la demi-droite des x >0 est le double de la pente de la demi-droite des x<0.
Deux droites sont dites parallèles quand elles n'ont aucun point commun.

Ci-contre, un triangle de Moulton. On peut déplacer les points A, B, et C. L'axe des coordonnées est un simple repère.

On a ajouté une droite (MN) pour que l'on puisse constater que l'axiome de Pasch est bien vérifié.

On notera que le dessin des droites peut disparaître quand elles sont proches de la verticale. Cela est dû à la façon dont elles ont été construites. Ce problème n'existe pas pour les segments de la figure ci-dessous.

Le fait que le modèle ne vérifie pas le théorème de Desargues est plus parlant dans sa version dite « du tétraèdre » : on observera, dans la figure ci-contre, que la propriété de Desargues n'est pas vérifiée et que cette géométrie affine plane ne peut s'étendre à une géométrie affine de l'espace.

Dans la figure ci-contre, on peut déplacer A, B, C, A', B' et C'. Le point I est déterminé par l'intersection des droites (AA') et (BB') : il est dépendant en particulier de A'.
On notera que la gestion des pointillés n'est pas complètement dynamique. Elle est correcte pour B « devant » la droite de Moulton (AC).

Quand on réalise un modèle affine en géométrie dynamique, la première construction que l'on peut effectuer à partir de l'incidence et du parallélisme est le milieu de deux points A et B : c'est l'intersection des diagonales d'un parallélogramme AMBN. Cela peut se construire dans tout modèle de géométrie affine arguésienne. Mais dans le cas non arguésien, la situation est moins simple.

Étant donnés deux points A et B, et un point M, on construit la droite (AB) et le parallélogramme AMBN. En faisant varier M, on s'aperçoit que, contrairement à l'environnement affine usuel, le point d'intersection I des deux droites (AB) et (MN) n'est pas fixe : les diagonales ne se coupent pas en leurs milieux.
Par ailleurs, sur la droite (MN) quand elle est (usuellement) affine comme à l'ouverture de la figure, il est clair que I n'est pas le milieu (affine ordinaire) de M et N.

L'autre point important du cas non arguésien d'un plan affine est l'impossibilité de construire ce que Hilbert appelle une géométrie des coordonnées : Il s'agit de chercher à construire un corps de nombre K à partir des propriétés des axiomes de la géométrie, chaque point étant identifié à la donnée d'un ou plusieurs nombres. À ne pas confondre avec la géométrie analytique de Descartes qui, elle, utilise l'algèbre pour « analyser » les propriétés géométriques. Nous allons l'illustrer sur deux exemples. Tout d'abord en montrant, pour le cas élémentaire de la somme, la dépendance du résultat par rapport aux représentants choisis.
À partir de trois points A, B, C et d'un point A', on construit, par des parallélogrammes, ce qui pourrait être le translaté A'B'C' de ABC dans la translation qui envoie A en A'. Pour cela on a construit tout d'abord B' par le parallélogramme A'ABB' puis le point C' par le parallélogramme B'BCC'.

On constate sur la figure ci-dessous que l'on obtient un point C" différent du point C' en construisant le parallélogramme A'ACC".

En fait c'est simplement la réciproque du théorème de Desargues (version affine) qui n'est pas vérifiée : nous avons, par construction, (A'B') // (AB), (BC) // (B'C'), et les trois droites (AA'), (BB'), (CC') parallèles, mais (AC) n'est pas parallèle à (A'C').

Dans la figure ci-contre, on peut déplacer A, B, C et A'. On notera que, dans la configuration donnée au départ, les points C' et C" sont confondus pour une pente de (AC) négative ou nulle.
Toujours depuis la configuration de départ, le point C' semble indépendant de la position de B mais ce n'est pas le cas dès que la pente de (AB) devient positive.

Autrement dit, les éventuels vecteurs (les couples de bipoints que traditionnellement on définit comme équivalents dans la configuration du parallélogramme) et les sommes vectorielles associées ne sont pas indépendantes de leurs représentants : la relation sous-jacente n'est pas transitive.
Les translations n'ont pas les propriétés usuelles, et en particulier ne sont des collinéations : l'image d'une droite n'est pas une droite.

Ci-contre on se propose de construire l'image d'un point par une - éventuelle - homothétie de centre O transformant A en A' par le procédé affine usuel utilisant le parallélisme (en particulier le fait que l'image d'une droite est une droite parallèle).

On construit M' image de M, puis N'1 et N'2 images de N à partir de M et M' d'une part, puis de A et A' d'autre part. Là encore, avec des droites concourantes, deux couples de droites deux à deux parallèles, il n'y a pas coïncidence entre les points N'1 et N'2 comme dans le cas d'un plan affine arguésien.

C'est bien la non réciproque du théorème de Desargues, mais cette fois-ci dans le cas des droites concourantes.

Après la translation, l'homothétie n'est pas non plus une bonne candidate pour être une application ayant du sens dans cette géométrie.

3. Congruences

3.1 Sur les angles et la congruence

En dehors des points de l'axe des ordonnées, on peut dire que localement, autour d'un point, le plan de Moulton est euclidien. Donc localement on peut parler d'angle. Autrement dit, sauf en dehors des points de l'axe des ordonnées sur lesquels nous reviendrons, l'angle en le sommet d'un triangle existe et c'est l'angle euclidien.
De même, localement, quand on ne franchit pas l'axe des ordonnées, la longueur d'un segment existe, et c'est la longueur euclidienne. L'article de Moulton¹ se propose de construire un exemple simple d'un plan non arguésien qui vérifie tous les autres axiomes de Hilbert du plan affine.
Comme le propos de Hilbert est de reconstruire la géométrie euclidienne, il s'intéresse très vite aux angles et aux longueurs. Les droites de Moulton étant isomorphes aux droites réelles, le groupe d'axiomes sur l'ordre est trivialement vérifié.

Le groupe d'axiomes sur les congruences se décline en un premier sous-groupe de trois axiomes dits « de congruence linéaire », sur les segments, et un second sous-groupe de deux axiomes sur les angles, dont celui noté III.5 selon la terminologie des dernières éditions, qui lie les segments et les angles : c'est cet axiome qui est primordial pour la démonstration du théorème de Desargues dans le plan.

Pour que les axiomes sur la congruence soient vérifiés, il suffit de définir la longueur d'un segment de Moulton qui franchit l'axe des ordonnées. La solution naturelle retenue par Moulton est de choisir la somme des longueurs des deux segments euclidiens qui composent le segment de Moulton. C'est d'ailleurs la seule solution possible si l'on veut de plus, comme le souhaitait Moulton, que les autres axiomes (celui d'archimédie en particulier, pour la continuité) soient vérifiés.

Pour les angles, le seul problème réside dans le cas d'un angle ayant un sommet sur l'axe des ordonnées puisqu'il y a rupture de direction à cet endroit. En particulier, comme nous allons le voir plus loin, le plan de Moulton est non conforme en ces points. Moulton choisit une définition des angles en ces points - exposée plus loin - afin que l'axiome de congruence III.4 soit vérifié dans tout le plan.

(1) texte original disponible dans la partie Références

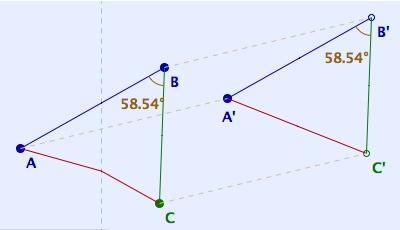
Il est facile de voir alors que l'axiome de congruence qui lie les longueurs et les angles (axiome III.5 des Fondements de Hilbert), n'est bien entendu pas vrai dans le plan de Moulton :

Ci-contre (illustration statique) un triangle ABC et un triangle A'B'C' avec, dans le plan euclidien, AB = A'B', BC = B'C' et l'angle en B égal à l'angle en B' (on a fait une translation euclidienne dans un contexte où les segments concernés sont aussi des segments du plan de Moulton).

Dans ce contexte, l'axiome de congruence voudrait que les angles en C de ABC et en C' de A'B'C' soient égaux. Comme localement ce sont les angles euclidiens, l'axiome de congruence est mis en défaut sur cette illustration.

Le premier théorème montré par Hilbert avec l'axiome III.5 est celui qui dit que si dans un triangle ABC les côtés AB et AC sont congruents, alors c'est aussi le cas des angles en B et C (propriété du triangle isocèle).

Ci-contre on a pris A et C deux points d'un cercle euclidien de centre B. En s'arrangeant pour que les segments de Moulton [BA] et [BC] restent euclidiens et que [AB] ne soit pas un segment euclidien, on vérifie immédiatement que cette première conséquence n'est pas vérifiée.

Sur la figure ci-contre on peut modifier les emplacements de A et C pour vérifier aussi que dans le cas euclidien usuel on retrouve bien le théorème des triangles isocèles (et la somme des angles).

Ainsi le premier théorème relatif aux côtés et aux angles d'un triangle n'est pas vrai. Les théorèmes de congruence des triangles (les cas d'égalité) qui en découlent ne sont pas non plus vérifiés dans le plan de Moulton.

3.2 La somme des angles d'un triangle de Moulton

Si le segment [AB] de Moulton n'est pas un segment euclidien, alors pour les points C au dessus - et tels que les segments de Moulton [AC] et [BC] soient euclidiens - la somme des angles du triangle de Moulton ABC sera inférieure à 180° et pour des points C en dessous de la droite euclidienne (AB) (avec les mêmes conditions), cette somme sera supérieure à 180° (il suffit de comparer par rapport au triangle euclidien ABC).

Il est d'ailleurs facile de calculer les valeurs extrêmes à partir de la définition des droites :

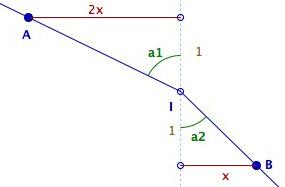
Pour les valeurs extrêmes de ce défaut d'angle, on est amené à considérer, dans le cadre de la figure ci-contre, les valeurs extrêmes de :
Pi-a1+a2 soit Pi-tan^-1(2x)+tan^-1(x).

En appliquant la fonction tangente croissante et les formules de trigonométrie usuelles, cela revient à chercher pour quelle valeur de x positif le minimum de la fonction f telle que f(x) = -x/(1+2x²) est atteint. On trouve alors sqrt(2)/2.

D'où, après simplification, le résultat suivant :

La valeur maximale possible pour la somme des angles d'un triangle est 180°+arctan(sqrt(2)/4) et la valeur minimale est 180°-arctan(sqrt(2)/4).

Ces valeurs sont réalisées par le triangle ABC de la figure suivante (selon la position de C, avec [AC] et [BC] euclidiens). Le triangle PQR permet d'explorer la somme des angles d'un triangle et d'approcher ces extrema.

Et si la somme des angles d'un triangle est supérieure à deux droits, peut-on avoir un triangle avec deux angles droits? La réponse est oui, avec une construction élémentaire comme ci-contre.

La somme des angles serait même maximale sur la base d'une configuration semblable à celle ci-dessus pour A et B.

Cela signifie aussi que dans certains cas, par un point M donné, il peut exister deux perpendiculaires à une droite donnée.

Et donc en ajoutant une parallèle à la droite (AB) passant par un point C, il en résulte qu'il existe des quadrilatères ayant 4 angles droits dont les autres côtés, [AD] et [BC] ne sont pas parallèles.

Sur la figure ci-contre on peut manipuler A, B et C pour tester les rectangles de Moulton, si on appelle encore rectangle un quadrilatère ayant 4 angles droits. On peut déplacer A - en conservant une abscisse négative - pour que l'angle en D ne reste pas droit ou placer C sous B pour que l'angle ne reste pas droit :

ainsi on peut constater qu'un quadrilatère peut avoir 3 angles droits et la somme de ses angles peut être inférieure ou supérieure à 4 angles droits.

On observera qu'on retrouve bien entendu la configuration euclidienne quand elle se présente.

3.3 Les longueurs dans le plan de Moulton

Comme déjà mentionné, la longueur d'un segment [AB] est sa longueur euclidienne si c'est un segment euclidien ou la somme des longueurs des deux segments euclidiens qui le composent sinon.

Dans la figure suivante on a construit un triangle ABC avec des angles en A et B égaux et dont les côtés correspondants ne le sont pas. Ainsi d'une part on est dans la non réciprocité du théorème sur les triangles isocèles : on peut avoir deux angles congruents sans que les segments correspondants le soient.
D'autre part cette figure illustre aussi la non véracité du cas de congruence des triangles ayant un côté congruent et les deux angles associés congruents respectivement : en effet en translatant, dans le plan euclidien les points A, B et la poignée, à droite de l'axe des ordonnées, on a un triangle MNP' avec MN congru à AB, les angles en A et M congrus, de même pour B et N.

Nous sommes donc bien dans la situation proposée en préambule où nous parlions d'un exemple où le mouvement, ici la translation, n'est pas représentatif de la congruence : c'est comme si les règles se déformaient en se déplaçant, ce qui correspondrait au cas des surfaces à courbure non constante dans un contexte de géométrie différentielle pour reprendre un autre exemple célèbre de Poincaré.

Cette figure, réalisée à des fins d'illustration de ce qui précède ne contient pas en elle-même ses propres tests de validité : elle ne rend compte de ce que l'on veut montrer que dans certaines conditions (que [AB] soit euclidien, A d'abscisse négative et C obtenu d'abscisse positive...)

Par ailleurs il est assez immédiat, même sans illustration, que cette longueur dans le plan de Moulton ne peut pas vérifier l'inégalité triangulaire : la distance utilisée n'est pas une métrique. Autrement dit, si le plan de Moulton est bien muni d'une distance, ce n'est pas un plan métrique.

Pour certaines définitions anglo-saxonnes de la distance, la longueur dans le plan de Moulton est bien une distance. En France elle pourrait parfois être appelée «semi-distance », la distance correspondant alors à une métrique.

Mais, pour ce qui nous occupe ici - en déplaçant C vers l'axe des ordonnées - cela éclaire le cas des angles dont un sommet est sur l'axe des ordonnées. On peut alors avoir A, C, B euclidiennement alignés alors que les points ne sont pas sur une droite de Moulton : il y a bien deux segments distincts qui font un angle qu'il convient maintenant de préciser.

3.4 Cas des angles ayant un sommet sur l'axe des ordonnées - Point de vue variationnel

Comme on vient de le constater concrètement sur l'exemple précédent, le modèle n'est pas conforme sur l'axe des ordonnées : les angles dans le plan de Moulton ne sont pas les angles euclidiens usuels pour un sommet I sur l'axe des ordonnées.

Dans la figure suivante, on peut vérifier qu'il y a une discontinuité dans la mesure de l'angle en M quand M traverse l'axe des ordonnées. La continuité invite à conserver une des deux mesures. Depuis Moulton, la tradition considère la réfraction des droites sur l'axe des ordonnées comme une rupture des droites venant des abscisses négatives, comme si un accident arrivait aux droites en franchissant l'axe des ordonnées. Dans cette conception, s'il s'agit de conserver l'une des deux mesures il est naturel de conserver celle des angles issus des droites euclidiennes provenant de la partie x < 0 des droites de Moulton. On pourrait tout aussi bien choisir l'autre mesure. La seule chose à faire est de choisir l'une des deux valeurs.

Autrement dit, l'angle de Moulton BIC - dans cette situation de deux droites de Moulton non euclidiennes - est l'angle euclidien A'IC'. Avec cette définition, l'axiome de congruence IV.4 (existence et unicité d'un angle congruent à un angle donné à partir d'une demi droite donnée) est vérifié y compris pour les points de l'axe des ordonnées.

3.5 Angles ayant un sommet sur l'axe des ordonnées - Point de vue absolu

Un autre point de vue, plus centré sur l'axiomatique de la géométrie, consiste à dire que, quelque soit la géométrie la mesure des angles est absolue : dans un plan, il y aura toujours un tour autour d'un point (360°) et un angle plat sera toujours la moitié d'un tour (soit 180°). Dans le cas des droites de Moulton, il suffit alors d'adapter la mesure des angles, généralement euclidienne en tout point autre que sur l'axe des ordonnées, au cas des points sur l'axe, et la définition précédente est alors tout à fait naturelle.

La figure suivante, sur l'exploration des angles, laisse entrevoir une difficulté pour la perpendiculaire à (AB) issue de M dans la position d'ouverture de la figure. La figure n'existe que pour M au-dessus de A et N en dessous de B. On peut placer néanmoins M sur (AB) à gauche de A et N sur (AB) à droite de B.

On peut mesurer alors le différentiel entre un plat euclidien et sa valeur dans le plan de Moulton (ci-dessous les droites sont les droites de Moulton passant par A et B respectivement et le sommet O).

3.6 Retour sur le triangle ayant trois sommets alignés d'un point de vue euclidien

En explorant la figure précédente traitant du non respect de l'inégalité triangulaire dans le plan de Moulton, il est naturel de placer C dans l'alignement euclidien de A et B : on a un triangle de Moulton bien particulier, avec trois angles que l'on sait maintenant mesurer . La figure suivante n'a de sens qu'en conservant A d'abscisse négative, sinon les points A, I , B sont « moultonement » alignés.

4. Orthogonalité

4.1 Perpendiculaire(s) à une droite issue d'un point

Puisque la notion d'angle est locale - autour d'un point autre que sur l'axe des ordonnées - il est tout naturel de définir deux droites comme orthogonales quand l'angle qu'elles forment à leur intersection est un angle droit. Clairement cette définition, si elle est correcte dans le cas général, va demander à être précisée sur l'axe des ordonnées. Nous avons déjà vu, à l'occasion de la congruence des angles, un cas de triangle ayant deux angles droits, et donc un cas de droite ayant deux perpendiculaires issues d'un même point.

La figure suivante se propose de laisser au lecteur le soin d'explorer cette notion de perpendicularité. On observera le cas où la pente est négative, mais aussi celui où elle est positive. On comprendra alors, en déplaçant finement P autour du point d'abscisse nulle, que la partie hachurée verte correspond aux différences entre l'angle droit incident de Moulton (quand P vient de la gauche de l'origine) à l'angle droit réfracté de Moulton (quand P vient de la droite de l'origine).

Continuité dynamique de la perpendiculaire principale

On aura observé ci-dessus la continuité - rendue par la couleur - de la perpendiculaire, même quand elle change brusquement de direction. Cette continuité vient du fait que c'est en réalité la même droite. Ce choix est nécessaire pour une réelle pertinence dynamique. Ainsi, quand on prend un point sur objet sur la perpendiculaire, ce point continue d'exister dans tous les cas où la perpendiculaire existe.

Bien entendu c'est le traitement conditionnel intégré aux coordonnées dans le logiciel qui permet d'avoir a priori une unique perpendiculaire, et éventuellement une seconde.

On observera un temps de latence du logiciel pour le point C quand la droite franchit la partie où il n'y a pas de perpendiculaire : le point C reste collé à la frontière de son existence... jusqu'à en retrouver une autre ensuite...

Nous avons vu le défaut d'angle des triangles du plan de Moulton, et ses valeurs maximales. D'un certain point de vue, c'est ce même défaut d'angle qui permet deux perpendiculaires à une droite, on empêche l'existence d'une perpendiculaire. Ce point de vue est topologiquement visible sur les droites de pente négative. Sur les droites à pente positive, il correspond à la différence entre l'angle euclidien du modèle et l'angle effectif du plan de Moulton pour un angle droit centré à l'origine comme à nouveau illustré ci-dessous :

4.2 Les hauteurs d'un triangle de Moulton

Il résulte de l'exploration précédente qu'un triangle peut, dans certaines circonstances, ne pas avoir trois hauteurs, et même n'en posséder qu'une seule comme c'est le cas de la figure suivante à son ouverture.

Dans cette figure, on a fait apparaître les parties vertes (pas de perpendiculaire) et rouges (deux perpendiculaires) pour les trois droites - même si la partie pour (BC) n'est pas visible à l'ouverture. Outre le comportement des hauteurs avec l'intersection ou la réunion des différentes parties coloriées du plan, on peut tester l'existence d'un orthocentre, comme point de concours de trois hauteurs. Quand il y a deux hauteurs issues d'un même sommet, une hauteur principale est en rouge, l'autre hauteur est en marron.

Chacun expérimentera qu'il est facile de produire des triangles de Moulton ayant un orthocentre.

4.3 Orthogonalité et distance minimale

Dans un contexte comme celui dans lequel nous évoluons, avec une distance qui n'est pas une métrique (pas d'inégalité triangulaire), la distance d'un point à une droite doit être précisée. En effet, elle est traditionnellement définie dans un espace métrique comme le minimum des distances du point aux points de la droite. Dans les environnements métriques classiques (y compris en géométrie hyperbolique ou elliptique), ce minimum est réalisé par la perpendiculaire à la droite issue du point (quand il y en a plusieurs comme en géométrie elliptique, les distances sont les mêmes; la droite est alors un cercle).

Or ici, nous avons deux nouveautés : le minimum de distance en tant que tel n'est pas nécessairement réalisé par un segment et ensuite, il existe des points depuis lesquels on ne peut pas mener de perpendiculaire à une droite.

Pour le premier phénomène, on choisit ici, entre chemin minimal et segment, de faire évoluer cette notion de distance minimale sur la branche du segment : on dira que la distance minimale entre un point M et une droite d est la longueur minimale réalisée par un segment MH pour H un point de d. Ceci étant précisé, dans certains cas, le minimum réalisé par un segment ne l'est pas par le segment orthogonal comme on peut le voir sur cette figure :

Par ailleurs, comme on peut mener deux perpendiculaires à une droite à partir de certains points, il convient de vérifier si les deux distances obtenues sont égales ou non. Or, dans la figure ci-dessous, les deux triangles rectangles euclidiens MHI et MKI ayant l'hypoténuse [MI] en commun, on ne peut avoir MH = MK que si HI = IK. En déplaçant M dans la figure suivante, on observera que la distance minimale dans le cas où il y a deux perpendiculaires est réalisée sur l'une ou l'autre branche. Contrairement à la situation précédente, le segment orthogonal est bien la solution pour le minimum car on est dans une situation localement euclidienne (les pentes des deux segments sont positives).

Cette première présentation dynamique du plan de Moulton est un résumé d'un autre article plus complet, à la fois sur ces thèmes mais aussi sur d'autres plus techniques comme les constructions de médiatrices et de bissectrices, ou encore sur le cercle de Moulton. La version longue présente aussi l'implémentation détaillée des droites de Moulton et des parallèles. Elle détaille la construction du cercle, du symétrique d'un point dans une symétrie centrale et propose au téléchargement un menu Moulton reprenant les principales macros utilisées pour réaliser ces figures.

5. Références

Sources primaires

HILBERT David (1971) - Les Fondements de la géométrie, éd. critique et trad. par Paul Rossier - Dunod
(1^re éd. : Grundlagen der Geometrie, Teubner, 1899).
Le modèle non arguésien initial proposé par Hilbert est à la page 126.
R éédition chez Gabay (1997). Sommaire disponible.

MOULTON Forest Ray (1902) - A simple non-Desarguesian geometry. Trans. Amer. Math. Soc. 3, 192-195.
Télécharger l'article original de Moulton (4 pages PDF)

MOUFANG Ruth (1932) - Die Schnittpunktsätze des projektiven speziellen Fünfecknetzes in ihrer Abhängigkei voneinander. Math. Ann. 106, 755-795.

MOUFANG Ruth (1933) - Die Desarguesschen Sätze von Rang 10. Math. Ann. 108, 296-310.

Sources secondaires

ARSAC Gilbert (1998) - L'axiomatique de Hilbert et l'enseignement de la géométrie au collège et au lycée - ALEAS & IREM de Lyon

CERONNI Cinzia (2004) - Non-Desarguian geometries and the foundationsof geometry from David Hilbert to Ruth Moufang - Historia Mathematica 31, 320-336
Un article qui résume parfaitement bien l'évolution de la problématique sur les années où elle a été très active.

VIENNE Lucas (1996) - Présentation algébrique de la géométrie classique. Vuibert
En particulier le chapitre V pour une lecture contemporaine de ces questions.

Sur CaR et CaRMetal, le magazine français sur CaR (de Éric Hakenholz)

http://db-maths.nuxit.net/CARzine/

Et son site sur CaRMetal (téléchargement, de nombreux tutoriaux, diaporamas)

http://db-maths.nuxit.net/CaRMetal/

Article de l'auteur de CaRMetal sur les interfaces en géométrie dynamique.

http://revue.sesamath.net/spip.php?article39

Une autre axiomatique, celle de Bachmann, en français, avec 148 figures téléchargeables faites en Cabri-géomètre.

http://www.reunion.iufm.fr/Dep/mathematiques/Formateurs/Yves/ch4bachmann.html

On trouvera en particulier (p. 337) un modèle affine où les droites sont des paraboles de notre plan euclidien, et plus loin (p. 341) un modèle borné de géométrie euclidienne qui a la particularité d'avoir la même représentation des droites qu'un autre modèle elliptique - mais pas la même interprétation.

Géométrie absolue (métrique et arguésienne) en CabriJava

http://www.reunion.iufm.fr/Dep/Mathematiques/abracadabri/abraJava/GNECJ/index.html (Miroir à La Réunion)

http://www-cabri.imag.fr/abracadabri/abraJava/GNECJ/index.html (Miroir à Grenoble)

CultureMATH accueil - contact

CultureMATH
accueil - contact