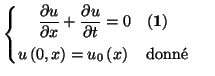
Petits pièges de la simulation numérique

La simulation numérique ne pose pas toujours seulement des problèmes de capacités de calcul : même avec des ordinateurs de plus en plus puissants, l'opération laisse encore des problèmes au mathématicien ! Il s'agit en effet de mettre en place des algorithmes qui fonctionnent, et nous allons voir que, même dans des cas très simples, on ne peut pas faire n'importe quoi.

Texte d'Emmanuel Grenier, ENS Lyon. Version ps ou pdf.

Vous trouverez ci-dessous des illustrations des phénomènes décrits dans ce texte.

Introduction

Nous nous intéressons ici au système différentiel suivant :

L'équation aux dérivées partielles (1) est appelée équation de transport. En effet nous savons trouver la solution exacte de ce système, à savoir la fonction :

Pour un résolution numérique, on cherche à discrétiser tout ceci. C'est-à-dire que l'on désire calculer des valeurs approchées de la solution u en un certain nombre de points (discrétisation en la variable spatiale x), typiquement les multiples du pas h choisi. Et ce uniquement à des moments successifs donnés (discrétisation en temps : on se donne un pas temporel k).
Comme on connaît la valeur initial de la solution u, toute la difficulté consiste à trouver un moyen d'exprimer les valeurs de u aux points voulus à l'instant t_n+1 en fonction de ses valeurs en ses points à l'instant t_n.
Pour la suite, on notera u_iⁿ l'approximation de u au point i h, et à l'instant n k.
Discrétiser l'équation, c'est alors remplacer les différentes dérivées de u par des valeurs approchées : ainsi la dérivée de u par rapport à t, au point u_iⁿ, sera remplacée par le rapport (u_iⁿ⁺¹ - u_iⁿ)/k, c'est-à-dire le taux d'accroissement correspondant.

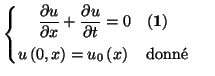
Enfin, nous allons illustrer dans le cas où la donnée initiale est de type "échelon", c'est-à-dire une fonction en escalier, nulle partout sauf sur un intervalle sur lequel elle est constante, égale à 1.

Un premier essai : schéma centré

Une bonne approximation de la dérivée spatiale en u_iⁿ (par rapport à la variable x) est le rapport : (u_i+1ⁿ - u_i-1ⁿ)/2h. L'équation de transport discrétisée est alors :

(u_iⁿ⁺¹ - u_iⁿ)/k + (u_i+1ⁿ - u_i-1ⁿ)/2h = 0

C'est le modèle utilisé dans l'illustration ci-contre. Disponible également, le programme transport, version matlab ou scilab, dans lequel on a pris les valeurs h=0.02 et k=0.01. Mise à part la donnée initiale qui n'est pas la même, ceci correspond au schéma (7) du texte d'Emmanuel Grenier.

Code source de l'applet.

Deuxième essai : schéma décentré à droite

La discrétisation précédente n'est pas symétrique en temps et en espace, les deux dérivées étant discrétisées différemment. Essayons donc cette fois de remplacer la dérivée spatiale en u_iⁿ (par rapport à la variable x) par le rapport (u_i+1ⁿ - u_iⁿ)/h. Notre équation de transport, ainsi discrétisée, devient :

(u_iⁿ⁺¹ - u_iⁿ)/k + (u_i+1ⁿ - u_iⁿ)/h = 0

Là aussi, ce modèle est illustré ci-contre. Disponible également, le programme transport2, version matlab ou scilab, dans lequel on a pris les valeurs h=0.02 et k=0.01. Ceci correspond au schéma (8) du texte d'Emmanuel Grenier.

Code source de l'applet.

La solution : schéma décentré à gauche

Voyons enfin ce qui se passe lorsque la dérivée spatiale en u_iⁿ est approximée par le rapport : (u_iⁿ - u_i-1ⁿ)/h. L'équation de transport discrétisée est alors :

(u_iⁿ⁺¹ - u_iⁿ)/k + (u_iⁿ - u_i-1ⁿ)/h = 0

Ce modèle fonctionne, comme l'illustre l'applet ci-contre. Disponible également, le programme transport3, version matlab ou scilab, dans lequel on a pris les valeurs h=0.02 et k=0.01. Ceci correspond au schéma (9) du texte d'Emmanuel Grenier.

Code source de l'applet.

Pour l'explication des différences fondamentales entre ces différentes façons de simuler numériquement l'équation de transport, pour découvrir pourquoi les deux premières sont vouées à l'échec tandis que la troisième fonctionne assez bien, nous vous renvoyons bien sūr au texte d'Emmanuel Grenier.

Pour revenir à tous les dossiers