coalescent-de-kingman

Une part entière de la théorie des probabilités est consacrée à l'étude des modèles de populations utilisés en biologie. A l'aide de ces modèles, on essaie d'estimer des quantités dont l'observation directe est difficile, de prévoir l'avenir, ou de tester une hypothèse théorique. Mais un modèle mathématique est construit sous de nombreuses hypothèses simplificatrices, il faut donc toujours garder du recul sur les résultats obtenus. Il y a une grande différence entre la réalité et la construction mathématique censée s'en approcher. Dans le modèle de nombreux effets sont négligés ce qui rend les calculs plus simples, mais les résultats faux. Cela peut toutefois suffire pour obtenir des ordres de grandeurs. De nombreux modèles différents sont bien entendu nécessaires pour reproduire toute la diversité du monde vivant. Nous nous intéresserons uniquement à l'un d'entre eux, un modèle aléatoire assez simple : le modèle de Wright-Fisher.

Le but sera ici d'étudier l'arbre généalogique d'une population qui évolue en suivant le modèle de Wright-Fisher. Cet arbre généalogique est bien entendu aléatoire également. Nous étudierons alors comment il évolue lorsque la population considérée devient très grande. Nous en tirerons un modèle limite, le coalescent de Kingman, qui se dégage naturellement de cette étude. Ce modèle décrit l'arbre généalogique d'un nombre fini de lignées choisies au hasard dans une population ambiante infinie. On choisi $n$ individus dans une population de $N$ individus et on étudie l'arbre généalogique de leurs lignées, et on fait tendre $N$ vers $+\infty$ en gardant $n$ fixé. Le modèle obtenu est suffisamment simple pour autoriser des calculs nous permettant, par exemple, de déterminer une borne sur l'âge de l'ancêtre commun de ces lignées.

L'étude de la généalogie des populations est nécessaire en biologie lorsqu'on s'intéresse au patrimoine génétique d'une population. On peut par exemple se demander quand un gène est-il apparu au cours du temps, ou si un certain type de mutations a un impact sur les individus ou si la mutation considérée du gène est neutre. J.F.C. Kingman apporta pour la première fois une réponse à cette question en 1981 dans ses article On the genealogy of large populations [Kingman, 1982a] et The coalescent [Kingman, 1982b]. Dans son étude, Kingman s'est intéressé à la généalogie de populations évoluant selon le modèle de Wright-Fisher. Nous introduirons tout d'abord ces deux modèles avant de calculer plusieurs quantités relatives au coalescent de Kingman : l'âge moyen du dernier ancêtre commun à une population, le nombre d'individus partageant la même mutation génétique, le nombre de descendants après un temps $t$ de l'ancêtre à la descendance la plus abondante, ou de celui ayant eu la descendance la plus faible, etc. Les résultats obtenus ont une application en biologie, par exemple grâce à la formule d'Ewens on peut tester l'hypothèse qu'une mutation est neutre ou non.

1. Introduction du coalescent de Kingman

1.1 Le modèle de Wright-Fisher

Dans tout ce qui suit, nous considérerons que chaque individu de la population que nous étudions descend d'un seul parent (haploïde), et possède le même patrimoine génétique que ce parent. Ainsi nous pouvons facilement définir des lignées d'ancêtres de nos individus. L'arbre généalogique est alors bien plus simple à décrire. Remarquons pour commencer que lorsque deux lignées ancestrales se rejoignent, elles restent communes pour toutes les générations précédentes. Cette remarque évidente est la raison pour laquelle le processus que nous étudierons sera appelé processus coalescent.

Dans le cas où un individu descend de deux parents, comme l'espèce humaine, nous pouvons par exemple appliquer ce modèle en nous intéressant uniquement aux relations mères-filles, afin de trouver la mère de toutes les femmes, l'Ève mitochondriale. De même on peut essayer de retrouver le père de tous les hommes, l'Adam-chromosome Y, dont le chromosome Y est l'ancêtre de celui de tous les hommes.

Introduisons maintenant le modèle de Wright-Fisher. Dans ce modèle, la taille de la population est supposée constante au cours du temps, égale à un entier $N$. La population évolue de génération en génération, à chaque étape tous les individus meurent, et donnent naissance à la génération suivante. De plus nous supposons qu'aucun individu particulier dans la population n'est favorisé par un quelconque avantage. Dans ce modèle, tout se passe comme si chaque individu choisissait parmi la population de la génération précédente son père uniformément au hasard, indépendamment du choix des autres membres de la population et des liens de parenté de ses ancêtres ou descendants.

Regardé dans le sens conventionnel d'écoulement du temps, un individu a un nombre de descendants qui suit une loi dite binomiale de paramètres $N$ et $\frac{1}{N}$. Autrement dit chaque enfant a une chance sur $N$ d'être le fils d'un parent donné. Mais on n'a alors pas d'indépendance du nombre d'enfants de chaque parent à une génération donnée. La connaissance du nombre d'enfants d'un individu particulier modifie la loi du nombre d'enfant de chacun des autres de sa génération. Par exemple savoir qu'un individu donné a eu $N$ enfants nous permet de déduire qu'aucun des autres n'en a eu, puisque la population est supposée constante au cours du temps. A contrario, le fait de savoir quel parent a choisi un individu n'influence aucunement le choix des autres : lorsqu'on remonte le temps, le processus s'exprime en termes d'évènements indépendants. Il est par conséquent plus simple de réaliser des calculs en remontant dans le temps. Ce modèle est donc parfait pour étudier la généalogie d'une population.

Figure 1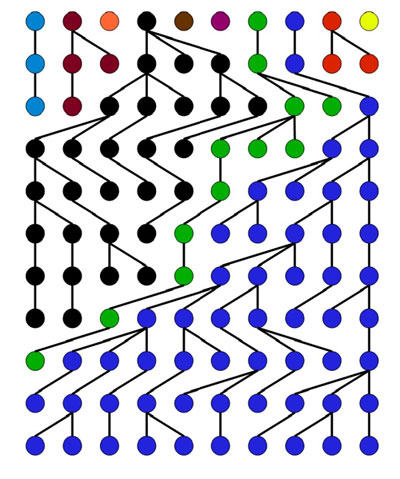

Évolution au cours du temps d'une population selon le modèle de Wright-Fisher, avec l'indication des descendants de la première génération.

1.2 Étude fine de la généalogie

Nous allons maintenant étudier l'arbre généalogique d'un échantillon d'une population se reproduisant selon le modèle de Wright-Fisher. Rappelons pour commencer une remarque simple : lorsque deux lignées généalogiques admettent un ancêtre commun à une génération donné, les lignées restent confondues pour toutes les générations précédentes.

Considérons pour commencer deux individus dans une population ambiante de $N$ personnes. La probabilité pour que ces deux individus soient des frères est égale à $\frac{1}{N}$. En effet, il y a $N^2$ choix possibles de parents pour chacun des deux individus, et pour $N$ de ces choix, le parent choisi est le même. Dès lors, la probabilité pour que deux individus ne soient pas frères est de $1-\frac{1}{N}$. On s'intéresse alors à la probabilité que leur grand-père soit différent. Il faut que leurs pères soient différents, et que les pères de ceux-ci soient différents. Or connaitre les enfants d'une génération n'influence pas les liens de parenté de la génération précédente. Par conséquent la probabilité que les grand-pères des deux enfants soient différents est égale à $(1-\frac{1}{N})^2$. Ce résultat peut se généraliser sans difficulté. On appelle la lignée d'un individu le chemin reliant un individu à ses ancêtres successifs. La probabilité pour qu'après $k$ générations, deux lignées choisies soient toujours distinctes est égale à $(1-\frac{1}{N})^k$.

Nous pouvons de la même façon calculer quelle est la probabilité que $l$ lignées restent toutes distinctes pendant $k$ générations. Commençons par nous intéresser à une seule génération. Nous considérons alors les liaisons parent-enfant permettant de laisser les $l$ lignées distinctes. Le premier individu choisit son parent, puis le second parmi les $N-1$ parents restants, le troisième parmi les $N-2$ restants, etc. En définitive nous obtenons que la probabilité que $l$ lignées choisies restent distinctes après une génération est égale à :

$\displaystyle{\frac{N(N-1)\cdots (N-l+1)}{N^l}= (1-\frac{1}{N})\cdots(1-\frac{l-1}{N}).}$

De même après $k$ générations, la probabilité que nos $l$ lignées soient restées distinctes est alors égale à $\big[(1-\frac{1}{N})\cdots(1-\frac{l-1}{N})\big]^k$.

Figure 2
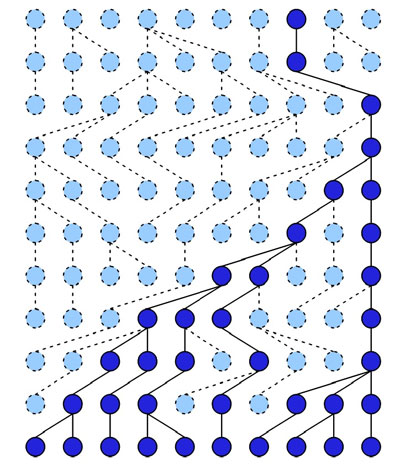Les lignées du modèle de Wright-Fisher, remontées au cours du temps.

Nous pouvons maintenant introduire le coalescent de Kingman. C'est un processus construit comme une limite des arbres généalogiques d'échantillons de taille finie dans une population ambiante de plus en plus grande, tendant vers $+\infty$. Bien sûr, après une génération il n'y a plus aucune chance pour que deux individus pris au hasard soient frères, car on a $\frac{1}{N} {\longrightarrow} 0}$ quand $ {N {\longrightarrow} +\infty}$. Pour éviter cette situation triviale, nous allons prendre une limite d'échelle : en même temps que la population grandira, nous accélérerons le passage du temps, ce qui nous permettra d'obtenir une limite non-triviale. Ainsi, plutôt que de regarder le processus à $N$ individus à la génération $k$ fixée, nous regarderons pour tout $t \in \mathbb{R^+}$ le processus à $N$ individus à la génération $\big\lfloor{Nt}\big\rfloor$ ($\big\lfloor{.}\big\rfloor$ désigne la partie entière, le plus grand entier inférieur ou égal à ce nombre).

Ce processus n'a pas forcément d'interprétation biologique simple. Mais lorsque nous nous intéresserons à une population de taille $N$ donnée, on pourra approximer son comportement par celui d'un coalescent de Kingman, et exporter les résultats de la manière suivante : si l'on trouve par exemple un ancêtre commun à l'instant $t$, dans le modèle "réel", cela correspond à un ancêtre commun à la génération $Nt$. Nous allons alors avoir besoin d'un résultat classique sur les limites.

Propriété 1.1. Soit $x \in \mathbb{R}$, on a : $\displaystyle{\lim_{n \to +\infty} \left(1+\frac{x}{n}\right)^n = e^x.}$

Démonstration. Soit $x \in \mathbb{R}$ et $n \in \mathbb{N}$, on pose $u_n=(1+\frac{x}{n})^n$ et $v_n=\ln u_n$. On a :

$\displaystyle{v_n = n \ln\left(1+\frac{x}{n}\right) = x\frac{\ln(1+\frac{x}{n})-\ln(1)}{\frac{x}{n}}.}$

Or $x \mapsto \ln x$ est dérivable en 1 de dérivée égale à 1, par conséquent on a :

$\displaystyle{\lim_{n\to +\infty} v_n = x,}$

d'où, par continuité de $x\mapsto e^x$ on obtient :

$\displaystyle{ \lim_{n\to +\infty} u_n = e^x.}$

Figure 3
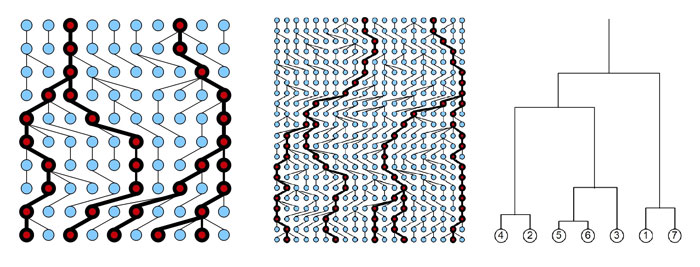Le coalescent de Kingman comme limite d'échelle d'arbre généalogiques.

En utilisant cette propriété nous remarquons alors que la probabilité que, dans le processus limite, deux individus aient des lignées distinctes jusqu'au temps $t$ est égale à $\lim_{N \to +\infty} (1-\frac{1}{N})^{\lfloor{Nt}\rfloor}=e^{-t}$. En particulier, la probabilité que deux individus n'aient aucun ancêtre commun est égale à 0, car dans ce cas les lignées sont distinctes pour tout $t\in \mathbb{R}^+$, donc en particulier quand $t \to +\infty$. En d'autre terme, si on note $T$ l'âge (aléatoire) de l'ancêtre commun de ces deux individus choisis dans la population, on a :

$\displaystyle{P(T>t) = e^{-t}.}$
Définition 1.1. Une variable aléatoire $e$ est dite de loi exponentielle de paramètre $\lambda>0$ si c'est une variable aléatoire à valeurs dans $\mathbb{R}^+$ vérifiant pour tout $t\geq 0$ :

$\displaystyle{P(e>t) = e^{-\lambda t}.}$

Autrement dit $T$ est une variable aléatoire exponentielle de paramètre 1. Rappelons quelques propriétés très classiques des variables aléatoires exponentielles :

Propriété 1.2. Si $e$ est une variable aléatoire exponentielle de paramètre 1, alors $\frac{1}{\lambda}e$ est une variable aléatoire exponentielle de paramètre $\lambda$.
Si $e$ est une variable aléatoire exponentielle de paramètre $\lambda$, elle vérifie la propriété d'absence de mémoire, autrement dit :

$\displaystyle{P(e>t+s|e>t)= P(e>s).}$

Nous aurons également besoin tout au long de notre étude du lemme suivant.

Lemme 1.1. Soit $T_1, \cdots, T_k$ des variables aléatoires indépendantes de loi exponentielles de paramètres $t_1, \cdots, t_k$. On note $T$ le minimum de $T_1, \cdots ,T_k$ et $\alpha$ l'indice de la variable aléatoire réalisant ce minimum, c'est-à-dire que l'on a $T = T_\alpha$.
$T$ est une variable aléatoire exponentielle de paramètre $t_1+\cdots +t_k$, et $\alpha$ est une variable aléatoire indépendante de $T$, telle que $P(\alpha=i)=\frac{t_i}{t_1+\cdots +t_k}$.

Démonstration. On calcule simplement la probabilité que $\min T_1, \cdots, T_k$ soit plus grande que $t$ et que $\alpha = i$ :

$\displaystyle{P(\alpha=i, T>t) = P(T_i>t, \forall j \neq i T_j>T_i).}$

Cette dernière probabilité est une fonction de $T_i$, que l'on peut écrire de la manière suivante :

$\begin{eqnarray} P(\alpha=i, T>t) & = & \int_t^{+\infty} t_ie^{-t_i s} \prod_{j \neq i}P(T_j>s)ds\\ & = & \int_t^{+\infty}t_i e^{-t_1s -\cdots -t_k s} ds\\ & = & e^{-(t_1 +\cdots +t_k)t} \frac{t_i}{t_1+\cdots +t_k}. \end{eqnarray}$

Dès lors en prenant en particulier $t=0$ ou en sommant sur tous les indices allant de 1 à $k$, on voit que $T$ et $\alpha$ ont bien les lois que nous avions annoncé, de plus ces deux variables aléatoires sont bien indépendantes. Ce lemme est parfois appelé Lemme des réveils, car si on considère ces variables aléatoires $T_1, \cdots T_k$ comme $k$ réveils distincts, nous voyons que le fait de savoir que le premier des réveils ait sonné à un instant donné ne nous permet pas de dire de manière plus précise lequel des réveils a sonné. Par exemple, même si un réveil a tendance à sonner beaucoup plus tôt que les autres, le fait d'avoir attendu longtemps n'augmente ni ne diminue la probabilité que ce soit celui-ci qui ait sonné.

Ce lemme sera très important dans toute la suite, car nous travaillerons beaucoup avec des variables aléatoires exponentielles, et nous utiliserons sans arrêt ce résultat, ainsi que l'absence de mémoire des variables aléatoires de loi exponentielle.

Choisissons maintenant $k$ individus, on note $T_k$ le premier instant (aléatoire) auquel deux au moins des lignées généalogiques que nous étudions se rejoignent. Nous obtenons alors de la même manière que précédemment :

$\displaystyle{P(T>t)=\exp\left[ -(1+\cdots+(k-1))t \right]=\exp\left(-\frac{k(k-1)}{2}t\right),}$

car on vérifie immédiatement que $1 + \cdots + (n-1) =\frac{n(n-1)}{2}$ par récurrence.

$T_k$ est alors une variable aléatoire exponentielle de paramètre $\frac{k(k-1)}{2}$. Notons que lorsqu'on regarde $k$ lignées généalogiques distinctes, on peut trouver $\frac{k(k-1)}{2}$ paires de lignées généalogiques distinctes. Chacune d'entre elles peut se regrouper à des instants égaux à des variables aléatoires exponentielles de paramètre 1. Nous pouvons déterminer le premier instant auquel l'un de ces regroupements deux à deux se produit. Pour cela nous utilisons le Lemme 1.1.

Nous observons donc que si les instants auxquels les lignées se regroupent deux à deux sont indépendants, le premier instant auquel les deux premières de ces $k$ lignées se regroupent est aussi une variable aléatoire exponentielle de paramètre $\frac{k(k-1)}{2}$. On retrouve la quantité précédente, avec de plus l'information suivante : quand un changement arrive dans $k$ lignées, c'est forcément deux, et seulement deux de ces lignées choisies au hasard qui se regroupent.

Ce résultat a donc encouragé Kingman à introduire son modèle de coagulation dans lequel les seuls évènements de regroupement de lignées sont des regroupement deux à deux de lignées, indépendantes les unes des autres. La figure 3 illustre ainsi comment on sélectionne quelques individus dans une population de plus en plus grande. Le troisième graphe montre le processus obtenu lorsqu'on fait tendre la taille de cette population vers $+\infty$, en raccourcissant les longueurs des branches rouges de façon proportionnelle. L'arbre ainsi obtenu est appelé le processus coalescent de Kingman.

1.3 Construction du coalescent de Kingman

Notre processus d'intérêt, le coalescent de Kingman, est l'arbre généalogique d'une population de $n$ individus. En particulier, il décrit qui est plus proche parent avec qui, et quel âge a l'ancêtre commun de chaque paire d'individus. Dans le modèle de Kingman, si il reste $k$ ancêtres à l'instant $t$, alors au bout d'un temps exponentiel de paramètre $\frac{k(k-1)}{2}$, deux lignées choisies au hasard parmi toutes se regroupent en une seule. Ce processus s'appelle processus coalescent, car lorsque deux lignées se rassemblent, elles restent ensemble pour toujours, comme collées.

Figure 4
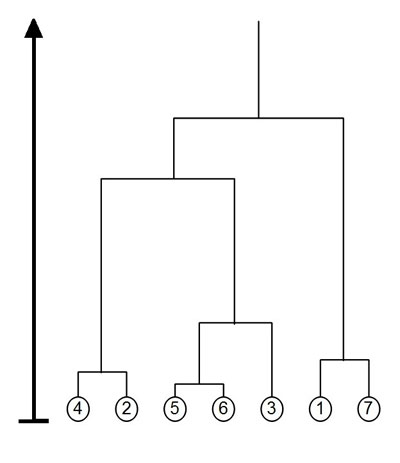Une représentation du coalescent de Kingman à 7 individus.

Dans ce modèle, chaque paire de lignées se regroupe après un temps exponentiel de paramètre 1, indépendamment des autres individus. La figure 4 est une représentation du coalescent de Kingman, l'axe indique le temps qui remonte dans le passé, et la longueur avant que deux lignes se rejoignent représente le degré de parenté entre les individus situés à l'extrémité. Afin de définir plus précisément les paramètres du modèle et de pouvoir réaliser des calculs, nous allons avoir besoin de quelques notions sur les espaces de partitions, avec lesquelles on code cet arbre généalogique.

2. Le coalescent de Kingman

Pour construire le coalescent de Kingman, nous avons besoin d'une manière de coder un arbre généalogique. Il faut en particulier écrire lesquelles de ces lignées se rejoignent à un instant donné, et à quel instant ces lignées se rejoignent. Pour cela nous allons, à chaque instant $t$ associer les sous-ensembles de la population initiale constitués des descendants des lignées existantes à la génération $t$. Plus précisément, l'ensemble $\{\{1,2\},\{3\},\{4\}\}$ décrit une situation où les individus 1 et 2 descendent de la même lignée lorsqu'on remonte à l'instant $t$, mais d'une lignée distincte de celles des individus 3 et 4. Si la partition suivante est $\{\{1,2,4\}\{3\}\}$, alors cela signifie que la lignée commune à 1 et 2 et celle de 4 se rejoignent avant qu'on ait trouvé un lien de parenté avec 3. De plus, l'instant auquel deux lignées se rejoignent, qui est aussi l'âge de l'ancêtre commun le plus récent de ces deux lignées, est donné par l'instant auquel on a un changement dans la répartition des ensembles. En quelque sorte, on représente un ancêtre à la génération $t$ par l'ensemble de ses descendants. La figure 5 correspond aux relations entre l'arbre généalogique associé au coalescent de Kingman et les partitions présentes dans le coalescent.

Figure 5
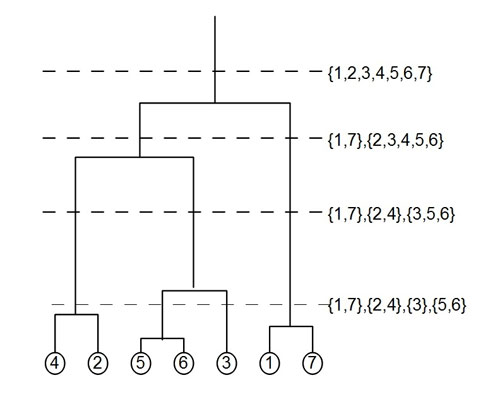Quelques partitions associées au coalescent de Kingman.

Nous allons commencer par préciser quelques propriétés relatives aux partitions. Nous les utiliserons par la suite pour construire un coalescent de Kingman partant d'une infinité d'individus à l'instant initial.

2.1 Quelques notions sur les espaces de partitions

Nous souhaitons construire l'arbre généalogique de $n$ individus. Pour cela, à chaque instant $t$, nous associons la partition de cette population constitué des descendants des lignées existantes $t$ générations dans le passé. Une partition des entiers entre 1 et $n$ est un certain nombre de sous-ensembles deux à deux distincts (aucun entier n'est dans deux ensembles à la fois, aucun individu ne descend de deux lignées à la fois) et dont l'union donne tous les entiers (tout le monde possède un ancêtre). L'ensemble de ces partitions est noté $P_n$.

Soit $\pi \in P_n$ une partition des entiers entre 1 et $n$, on note $#\pi$ le nombre d'ensembles présents dans cette partition, correspondant au nombre de lignées restantes. Nous avons par exemple, dans la partition suivante $#\{\{1,3,4,6\},\{2,5,7\}\} = 2$. Notons que la partition correspondant à la population initiale est la partition en singletons : une partition dans laquelle chaque individu correspond à une lignée. Nous allons maintenant préciser comment passer d'une partition à une partition plus ancienne. Lorsqu'un évènement de coagulation arrive, deux lignées choisies uniformément au hasard se rejoignent. Par conséquent, on passe d'une partition à une partition plus ancienne en réalisant la réunion de deux des ensembles présents pris au hasard.

Nous allons maintenant détailler une autre propriété des arbres généalogiques, qui se traduit sur les partitions qui sont associées. On peut passer de l'arbre généalogique à $n$ individus à celui à $n-1$ individus simplement en oubliant le $n^{ième}$ individu. On dira que deux arbres de $n$ et $k \leq n$ individus sont compatibles si l'arbre généalogique des $k$ premiers individus du grand arbre est égal au petit arbre. Cela se traduit de la manière suivante sur les partitions : à tout instant $t$, la partition des entiers entre 1 et $k$ obtenue en prenant les intersections des ensembles de la partition associée au grand arbre avec l'ensemble $\{1, \cdots k\}$ est égale à la partition associée au petit arbre.

Figure 6
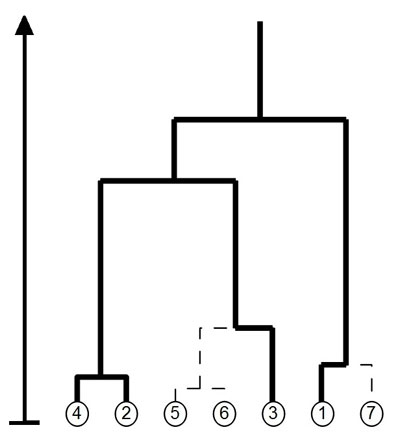Le sous-arbre des quatre premiers individus de notre population.

Cette remarque est importante, car elle permet non seulement de descendre (à partir d'un arbre généalogique, on peut retrouver l'arbre généalogique d'une partie de la population concernée) mais également de remonter vers un arbre de taille infinie. En effet, si on est capable de définir une suite d'arbres généalogiques de plus en plus grands et compatibles les uns avec les autres (comme le sont par exemple les arbres de la figure 6, le petit arbre en gras et le plus grand contenant également les pointillés) ; alors on est capable de définir les liens de parenté d'une famille infinie d'individus. Plus précisément, deux arbres sont dits compatibles lorsque la propriété suivante est vérifiée : le sous-arbre du plus grand arbre constitué des individus présents dans l'arbre le plus petit (celui des individus 1 à 4 par exemple) correspond exactement avec le plus petit arbre. En fait, si on cherche un renseignement dans n'importe lequel des deux arbres, soit celui-ci n'existe pas dans l'un des deux arbres, soit il est exactement le même pour les deux. Dans ce cas, si on peut fournir toute l'information permettant de réaliser l'arbre de n'importe quelle famille finie, on peut alors également fournir l'arbre généalogique infini, en ajoutant une nouvelle branche à chaque nouvel individu découvert. C'est ce que nous allons formaliser par la suite.

Pour réaliser cette remontée, on raisonne de la manière suivante : partons d'une suite $(\Pi^n)_{n \in \mathbb{N}}$ d'arbres généalogiques compatibles tel que $\Pi^n$ parte de $n$ individus à l'instant initial. A chaque instant $t$, on regarde la suite de partitions associée $(\Pi_{t}^{n})_{n \in \mathbb{N}}$. On construit alors la partition de $\mathbb{N}$ qui soit compatible avec toutes les partitions finies de la manière suivante. Deux entiers $p$ et $q$ sont situés dans le même ensemble si et seulement si pour tout entier $m$ plus grand que $p$ et $q$, ces deux entiers sont situés dans le même ensemble de $\Pi_t^m$. Cette partition infinie permettra de construire un arbre généalogique sur une population infinie. En effet nous obtenons pour chaque instant $t$ une partition infinie $\Pi_t$, et le passage d'une partition à une partition plus ancienne se fait forcément par la réunion d'un certain nombre d'ensembles. Nous avons donc bien un arbre généalogique.

2.2 Le coalescent de Kingman, construction détaillée

Commençons donc la construction de l'arbre généalogique d'une population de $n$ individus. Cet arbre généalogique sera appelé le \textit{$n$-coalescent de Kingman}. À chaque instant $t$, on associe la partition $\Pi_t$ de $n$ correspondant aux lignées restantes lorsqu'on remonte de $t$ dans le temps.

On a clairement $\Pi_0=\{\{1\},\cdots \{n\}\}$, la partition associée à l'instant $0$ est constitué des $n$ ensembles disjoints. Nous attendons alors un temps exponentiel de paramètre $\frac{n(n-1)}{2}$, puis deux individus choisis uniformément au hasard sont regroupés dans un même ensemble. De manière plus générale, si à un instant donné il reste $k$ ensembles (on a $#\Pi_t = k$), on attend un temps exponentiel de paramètre $\frac{k(k-1)}{2}$, puis on choisit deux des ensembles uniformément au hasard que l'on fusionne ensemble pour obtenir la partition suivante. Cela correspond à deux des lignées de la population qui, choisis uniformément au hasard se rejoignent.

Ce processus est bien défini pour tout entier $n$, notons $(\Pi_t^{(n)})_{t \in \mathbb{R}^+}$ ce $n$-coalescent de Kingman. Nous nous intéressons maintenant à $\Pi_{|k}^{(n)}$ le processus restreint à $k$ individus. Il est naturel d'espérer obtenir un $k$-coalescent de Kingman, puisque c'est un arbre généalogique, celui de $k$ individus pris dans une population infinie suivant l'évolution du modèle de Wright-Fisher. Par calcul sur les variables aléatoires exponentielles, on peut prouver le théorème suivant.

Théorème 2.1. Pour tout $n \geq 2$ et $k \leq n$, le processus $\Pi_{|k}^{(n)}$ est un $k$-coalescent de Kingman, un coalescent partant de $k$ individus à l'instant initial.

La preuve de ce théorème est donnée dans l'Encart 1. Il est donc possible de construire pour tout $n \in \mathbb{N}$ un $n$-coalescent de Kingman de telle manière que pour tout instant $t$, la suite des arbres généalogiques $n$-coalescents de Kingman $(\Pi^n)_{n \in \mathbb{N}}$ soit compatible. Il existe alors pour tout instant $t$ une partition infinie dont la restriction à $n$ vaut $\Pi_t^{(n)}$. On note cette partition $\Pi_t$. Le processus $(\Pi_t)_{t \in \mathbb{R}^+}$ est appelé processus coalescent de Kingman. Il est caractérisé par la propriété suivante :

$\displaystyle{ \forall n \in \mathbb{N}, {\Pi_t}_{|n}}$ est un n-coalescent de Kingman.

Il existe une unique loi pour ce processus, c'est pourquoi on l'appelle le coalescent de Kingman infini. Il est difficile de travailler directement avec ce processus, c'est pourquoi dans la plupart des preuves que nous verrons, nous nous intéresserons à des coalescents de Kingman de taille $n$ finie, puis nous passerons à la limite quand $n \to +\infty$ pour obtenir des résultats sur ce coalescent infini, ou bien nous raisonnerons par récurrence.

Le coalescent de Kingman est intéressant à étudier, car il "chapeaute" tous les arbres généalogiques de taille finie à la fois. Un résultat sur ce processus a donc une certaine importance, car on en déduit simplement un bon résultat sur tout les arbres de Kingman de taille finie.

3. Descente de l'infini du coalescent de Kingman

Considérons $\Pi$ un coalescent de Kingman partant d'un nombre infini d'individus. Ce processus descend de l'infini, c'est-à-dire que pour tout instant positif, le nombre d'ancêtres de la population est fini. C'est un résultat intéressant, car cela signifie que quelle que soit la taille de la population de laquelle nous partons, nous savons non seulement qu'ils ont un ancêtre commun, mais aussi que l'âge du dernier ancêtre commun est borné par une valeur indépendante de la taille de la population. En d'autres termes, que l'on prenne deux ou deux mille individus, l'âge du dernier ancêtre commun est inférieur à la même borne finie.

Nous nous intéresserons également à la vitesse de descente de l'infini de ce processus, car il se trouve que pour des instants assez petits, le nombre d'individus est assez bien approximé par une fonction déterministe.

3.1 Borne sur l'âge de l'ancêtre commun le plus récent

Afin de calculer l'âge de l'ancêtre commun le plus récent d'un coalescent de Kingman, la seule information dont nous ayons besoin est le nombre d'ancêtres de la population à chaque instant $t$. En effet, nous savons que nous avons atteint l'ancêtre commun le plus récent lorsqu'on atteint l'instant où il ne reste plus qu'une seule lignée dans le processus.

Notons $D_t^n$ le nombre de lignées distinctes à l'instant $t$ dans le $n$-coalescent de Kingman. Ce processus $(D_t^n)_{t \in \mathbb{R}^+}$ peut être décrit de la manière suivante. Nous avons $D_0^n=n$. Nous attendons alors un temps exponentiel de paramètre $\frac{n(n-1)}{2}$, à cet instant nous avons un évènement de coagulation, donc $D_t^n$ diminue de 1. Puis nous attendons un temps exponentiel de paramètre $\frac{(n-1)(n-2)}{2}$, et on diminue encore de 1, etc.

Posons $e_1, e_2, \cdots$ des variables aléatoires indépendantes exponentielles de paramètre 1. On pose, pour tout $k \leq n$ :

$\displaystyle{S_{n,k}=\sum_{i=k+1}^n \frac{2}{i(i-1)}e_i,}$

l'instant auquel le processus $D_t^n$ arrive dans l'état $k$. Grâce à la définition de $D_t^n$, $S_{n,k}$, le premier instant auquel $D_t^n$ vaut $k$, est bien la somme de variables aléatoires de paramètres $\frac{n(n-1)}{2}, \cdots, \frac{k(k-1)}{2}$ indépendantes, ce qui est la variable que nous avons décrite plus haut. Or $D_t^n \leq k$ indique que le premier instant auquel $D_t^n$ atteint $k$ est avant l'instant $t$, d'où nous tirons l'égalité suivante :

$\displaystyle{\mathbb{P}(D_t^n \leq k) = \mathbb{P}(S_{n,k}\leq t).}$

Nous allons maintenant nous intéresser au coalescent de Kingman infini. Le nombre de lignées de la population infinie présentes à la génération $t$ est clairement égal à la limite du nombre de lignées présentes dans les coalescents restreints à $n$, pour $n \to +\infty$. On pose $D_t= \lim_{n \to +\infty} D_t^n$ le nombre total d'individus à l'instant $t$ dans le coalescent de Kingman. Posons également

$\displaystyle{S_k=\sum_{i=k+1}^{+\infty} \frac{2}{i(i-1)}e_i,}$

nous pouvons donc maintenant passer à la limite quand $n \to +\infty$ d'un côté et de l'autre de l'inégalité. Des résultats de la théorie de l'intégration nous donnent :

$\displaystyle{\mathbb{P}(D_t \leq k) = \lim_{n \to +\infty} \mathbb{P}(D_t^n \leq k) = \lim_{n \to +\infty} \mathbb{P}(S_{n,k}\leq t) = \mathbb{P}(S_k \leq t).}$

Remarquons pour commencer que $S_k$ est une variable aléatoire d'espérance finie, donc qui est finie également. En effet :

$\displaystyle{E(S_k) = \sum_{i=k+1}^{+\infty} \frac{2}{i(i-1)} E(e_i) = \sum_{i =k+1}^{+\infty} \frac{2}{i-1} - \frac{2}{i} = \frac{2}{k}.}$

De plus $\lim_{k \to +\infty} E(S_k)=0$, donc on sait que la probabilité pour $S_k$ d'être plus grande que $t$ devient très faible pour $k$ très grand. Ceci nous indique que la variable aléatoire $D_t$ est, pour tout $t>0$ une variable aléatoire finie presque sûrement :

$\displaystyle{\mathbb{P}(D_t < +\infty) = \lim_{k \to +\infty}\mathbb{P}(D_t \leq k) = 1-\lim_{k\to +\infty} \mathbb{P}(S_k >t) = 1.}$

C'est un résultat très important appelé la propriété de descente de l'infini du coalescent de Kingman. Il signifie qu'en tout instant strictement positif, il ne reste qu'un nombre fini de lignées dans le coalescent. Et ce bien que l'on soit parti d'un nombre infini de lignées à l'instant 0. Autrement dit un nombre fini de lignées engendrent une population infinie. De plus, l'échantillon de population que nous regardons est grand, moins le nombre de lignées qui lui est associé croit, et on finit par atteindre un nombre maximal. Dans la prochaine section, nous verrons comment se produit ce phénomène de goulot d'étranglement, qui fait passer le nombre d'individus étudiés de l'infini à une quantité finie. Nous mettrons ainsi en évidence une \og vitesse de descente de l'infinie \fg{} du coalescent de Kingman, la vitesse à laquelle le nombre de lignées diminue lorsqu'on s'écarte de l'instant d'origine. On retiendra donc :

$\displaystyle{\forall t >0, D_t<+\infty }$ presque surement.

Le deuxième résultat intéressant est que nous obtenons la valeur de l'âge du plus récent ancêtre commun du coalescent de Kingman. En effet, cet âge est le temps d'atteinte de 1 pour le processus du nombre de blocs $D_t$. Posons $T$ l'âge de cet ancêtre commun, nous avons :

$\displaystyle{\mathbb{P}(T<t)= \mathbb{P}(D_t=1)= \mathbb{P}(S_1<t).}$

Nous obtenons par conséquent le résultat suivant :

$\displaystyle{T = \sum_{k=2}^{+\infty} \frac{2}{k(k-1)}e_k.}$

Nous pouvons calculer l'espérance de l'âge du plus récent ancêtre commun, nous avons $E(T)=2$. L'espérance étant fini, l'âge aléatoire est lui-même fini presque sûrement. Mais rappelons que l'arbre généalogique de tout échantillon de taille fini peut être considéré comme un sous-arbre du coalescent de Kingman, par conséquent l'âge de leur plus récent ancêtre commun est majoré par $T$, qui est une constante indépendante de la taille de l'échantillon. Autrement dit, il existe un âge au-delà duquel quelque soit l'échantillon choisi dans la population, on ne peut trouver deux lignées distinctes. Nous interprétons ceci comme l'âge de l'ancêtre commun de toute la population considérée.

Nous allons maintenant tenter d'appliquer les résultats obtenus sur notre modèle à une espèce réelle. Nous avons obtenu que l'âge de l'ancêtre commun d'une population infinie est en moyenne égal à 2. Cependant, dans notre modèle, nous avons accéléré le passage du temps d'un facteur proportionnel à la taille de la population considérée. Rappelons également qu'une unité du temps (discret) est égal à une génération. Par conséquent, si l'approximation de l'évolution de la vraie population par le coalescent de Kingman est assez précise, nous obtenons que l'âge du plus récent ancêtre commun d'un groupe de $N$ individus est en moyenne égal à environ $2 \times N$ générations dans le passé de ce groupe.

Lorsqu'on applique ce modèle à la population humaine, on obtient un nombre bien trop grand. Il y a six milliards d'êtres humains, et une génération humaine représente environ 25 ans. Mais nous avions également supposé dans notre modèle que la population ambiante restait constante au cours du temps, or la population humaine a cru à vitesse exponentielle durant plusieurs dizaines de siècles.Si on remonte d'une dizaine de milliers d'années, il y avait alors quelques milliers d'êtres humains seulement, et la taille de cette population évolue peu lorsqu'on remonte encore dans le passé, jusqu'à une centaine de milliers d'années. L'estimation que nous obtenons est de l'ordre de 50-60000 ans, bien plus raisonnable et proche des estimations biologiques de plusieurs généticiens, comme Spencer Wells [Ewens, 1972]. Mais les nombreuses approximations du modèle nous empêchent d'avoir une trop grande confiance dans cette estimation. Remarquons que cet âge correspond à celui de la mère de nos les mères, pas au premier ancêtre commun que l'on peut trouver à toute l'humanité, c'est à dire qui engendre toute l'humanité, mais à la fois par ses fils et ses filles. En effet cet individu, d'après la plupart des estimations aurait vécu aux environs de l'an 1000.

3.2 La vitesse de descente de l'infini du coalescent de Kingman

Nous allons maintenant étudier le nombre d'individus dans le coalescent de Kingman aux premiers instants. Ceci nous donnera le comportement du coalescent avec un très grand nombre d'individus. En fait, pour $t$ proche de $0$, on a environ $\frac{2}{t}$ individus. Pour cela, nous reprenons simplement l'évaluation précédente :

$\displaystyle{\mathbb{P}(D_t \leq k) = \mathbb{P}(S_k\leq t),}$

où on rappelle que $S_k=\sum_{i=k+1}^{+\infty} \frac{2}{i(i-1)}e_i$. Le temps d'atteinte du niveau $k$, que nous noterons $T_k$ est donc égal en loi à $S_k$.

Nous calculons alors :

$\displaystyle{E(T_k) = \sum_{i=k+1}^{+\infty} \frac{2}{i(i-1)} = \sum_{i=k+1}^{+\infty} \frac{2}{i-1}-\frac{2}{i} = \frac{2}{k},}$

$\displaystyle{Var(T_k) = \sum_{i=k+1}^{+\infty} \frac{4}{(i(i-1))^2} \sim \frac{4}{k^3}.}$

Connaissant l'espérance et la variance de $T_k$, nous pouvons calculer la probabilité que $T_k$ soit loin de $\frac{2}{k}$. Nous avons en effet :

$\begin{eqnarray} \mathbb{P}\left(\left|T_k-\frac{2}{k}\right|\geq \frac{\ln k}{k}\right) & = & \mathbb{P}\left(\left(T_k-\frac{2}{k}\right)^2\geq \left(\frac{\ln k}{k}\right)^2\right)\\ & \leq & \frac{k^2}{\ln k^2}E\left(T_k-\frac{2}{k}\right)^2\\ & \leq & \frac{C {\ln k}^2}{k}. \end{eqnarray}$

Nous allons maintenant utiliser un résultat très important et très utile de la théorie des probabilités, le lemme de Borel-Cantelli. Celui-ci postule que si les probabilités associées d'une suite d'évènements décroient assez vite alors, presque sûrement, il y a seulement un nombre fini de ces évènements qui sont vérifiés. Plus précisément :

Lemme 3.1.Soit $A_k$ une suite d'évènements. Si $\sum_{k=0}^{+\infty} \mathbb{P}(A_k) < +\infty$ alors on a :

$\displaystyle{\mathbb{P}(A_k \textrm{ n'est plus vérifié à partir d'un certain rang } k_0) = 1.}$

Démonstration.On considère, pour chaque entier $k$ la fonction $f_k$ qui vaut $1$ si $A_k$ est vérifié et 0 sinon. Dans ce cas, nous voyons que $\sum_{k =0}^{+\infty} \mathbb{P}(A_k)$ est l'espérance de la fonction $\sum_{k=0}^{+\infty} f_k$. Cette espérance est finie, donc la fonction l'est aussi (si la fonction était infinie, son espérance le serait aussi). Cela signifie en particulier que l'on est sur qu'au plus un nombre fini d'évènements sont vrais. Par conséquent, pour $k_0$ assez grand, $A_k$ n'est plus vérifié pour tout $k \geq k_0$.

Nous allons maintenant appliquer ce lemme à la suite des évènements :

$\displaystyle{B_p=\{\left|T_{p^2}-\frac{2}{p^2}\right|\geq \frac{\ln p^2}{p^2}\}.}$

On a vu précédemment que la probabilité d'un tel évènement est de l'ordre de $\frac{\ln p}{p^2}$, grâce au théorème de Bienaymé-Tchebychev la série des probabilités est donc convergente. Par conséquent, nous savons que presque sûrement, il existe un rang au delà duquel on a :

$\displaystyle{\left|T_{p^2}-\frac{2}{p^2}\right|\leq \frac{\ln p^2}{p^2}.}$

Par conséquent, nous avons :

$\displaystyle{\lim_{p \to +\infty} p^2 T_{p^2} = 2 \textrm{ presque sûrement},}$

On obtient donc pour tout entier $n$ compris entre $p^2$ et $(p+1)^2$ :

$\displaystyle{p^2 T_{(p+1)^2} \leq n T_n \leq (p+1)^2T_{p^2},}$

donc par théorème des gendarmes, nous obtenons $\lim_{n \to +\infty} n T_n = 2$ presque sûrement. Ce résultat se traduit de la même manière sur le processus du nombre de blocs $D_t$. On obtient :

$\displaystyle{\lim_{t \to 0} tD_t = 2 \textrm{ p.s.}}$

ce qui est bien ce que nous souhaitions démontrer, au voisinage de 0, $D_t$ se comporte comme $\frac{2}{t}$, il y a environ $N$ individus à l'instant $\frac{2}{N}$.

Ce résultat peut être précisé. Grâce à un résultat de la théorie des martingales, on peut prouver qu'en réalité, les $n$-coalescents de Kingman se comportent dans leurs premiers instants comme la fonction $t \mapsto \frac{2}{t+\frac{2}{n}}$. Ces résultats ont été développés par Julien Berestycki, Nathanaël Berestycki, et Vlada Limic, pour des classes plus générales de processus coalescents [Berestycki (J), Berestycki (N), et Limic, à paraître].

Nous allons maintenant nous intéresser au patrimoine génétique des individus, en fonction des mutations qui se répartissent le long de l'arbre généalogique.

4. Mutation neutre et classification phylogénique

Nous allons maintenant enrichir l'arbre généalogique des individus auxquels nous nous intéressons par un certain nombre d'évènements de mutation. Plus précisément, nous considérons que chaque individu, à chaque génération, a une probabilité (faible) de subir une mutation neutre. Une mutation neutre est sans impact sur le nombre de descendants que l'individu concerné peut avoir, mais se conserve comme une signature chez tous ses descendants. Nous allons maintenant nous intéresser aux ensembles d'individus qui possèdent les mêmes mutations, plutôt qu'à ceux qui descendent de la même lignée. C'est donc un changement radical dans notre étude du processus. Jusqu'ici nous nous intéressions uniquement au comportement du processus à un instant $t$ fixé. Maintenant, nous regardons le processus comme un arbre, achevé, qui remonte jusqu'à un ancêtre commun. Nous plaçons ensuite un certain nombre de marques sur les branches de cet arbre, et nous nous intéresserons au nombres de sous-groupes créés quand nous coupons les branches de l'arbre en ces marques.

Nous créons ces marques de la manière suivante : à chaque épisode de coagulation $t$, nous lançons une variable aléatoire exponentielle de paramètre $\frac{\theta}{2}$ pour chaque individu présent dans le coalescent. Si certaines de ces variables aléatoires sont plus petites que l'instant de coagulation suivant, nous marquons la branche associée aux individus concernés à une distance de l'instant $t$ donnée par la variable aléatoire exponentielle. Nous relançons ensuite une autre variable aléatoire exponentielle que l'on compare à la distance entre cet instant de mutation et l'instant de coagulation suivant, puis on continue. Un tel arbre est dit marqué par un processus de Poisson d'intensité $\frac{\theta}{2}$ par unité de longueur des branches.

Figure 7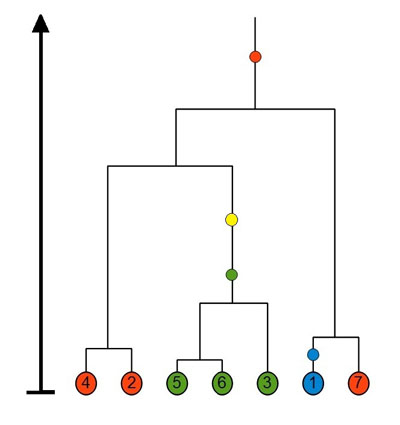
Un coalescent de Kingman marqué, avec les différents génotypes
indiqués par des couleurs.

Nous allons maintenant étudier comment $n$ individus choisis se répartissent en fonction des mutations qu'ils possèdent. Regardons précisément la dynamique de ces $n$ individus. Chaque individu va subir une mutation selon une loi exponentielle de paramètre $\frac{\theta}{2}$ et un évènement de coalescence peut arriver selon une loi exponentielle de paramètre $\frac{n(n-1)}{2}$. Grâce au Lemme des réveils, le premier de ces évènements arrive suivant une loi exponentielle de paramètre $\frac{n(n-1) + \theta n}{2}$, et c'est un évènement de coagulation avec une probabilité de $\frac{n(n-1)}{n(n-1) + \theta n}=\frac{n-1}{n-1+\theta}$, ou un évènement de mutation avec pour probabilité $\frac{\theta}{n-1+\theta}$. Dans ce cas, on considère la lignée ayant muté comme étant perdu, on l'oublie dans notre calcul suivant.

Plus généralement, si à un instant donné il reste $k$ individus, l'évènement suivant sera un évènement de mutation avec la probabilité $\frac{\theta}{k-1+\theta}$ et un évènement de coagulation avec une probabilité de $\frac{k-1}{k-1+\theta}$. Cet évènement arrivera selon une variable aléatoire exponentielle de paramètre $\frac{k(k-1) + \theta k}{2}$.

Nous allons maintenant réétudier notre parcours dans le sens opposé du temps. En fait, nous suivons alors le sens conventionnel du temps, du passé vers le futur, car dans le coalescent de Kingman nous remontions le temps. Nous partons de la mutation la plus récente de l'ancêtre commun de la population de $n$ individus. Le premier évènement qui arrive ensuite est une mutation avec la probabilité $\frac{\theta}{1+\theta}$ et une coagulation avec la probabilité $\frac{1}{1+\theta}$. En d'autres termes, le deuxième individu observé possède un génome différent avec une probabilité $\frac{\theta}{1+\theta}$, et possèdera les mêmes mutations que l'ancêtre commun avec la probabilité $\frac{1}{1+\theta}$. Le $k^\textrm{ième}$ individu qui arrive sera causé par une mutation avec la probabilité $\frac{\theta}{k-1+\theta}$, et possèdera donc une nouvelle mutation, qui le mettra à part de tous les autres, ou avec la probabilité $\frac{k-1}{k-1+\theta}$ sera causé par une coagulation. Dans ce cas, le nouvel individu sera le frère d'un individu existant choisi uniformément au hasard, et partagera donc exactement les mêmes mutations que lui.

Nous pouvons alors généraliser ceci pour tout entier $n$, donc pour la population infinie, qui se distribuera selon cette dynamique. Celle-ci s'appelle le processus du restaurant chinois, car il rappelle le processus suivant. Un client arrive dans un restaurant chinois et s'installe à la première table disponible. Un deuxième arrive. Avec la probabilité $\frac{1}{1+\theta}$ il connait le premier client et s'installe à sa table, sinon il s'installe à la table suivante. Un troisième client entre, il connait l'un des deux clients déjà attablés avec la probabilité $\frac{1}{2+\theta}$ et s'installe à la table de ce dernier dans ce cas-là, sinon il s'installe à la table suivante, etc.

Ce processus est exactement le même que celui selon lequel se créent les partitions correspondant aux mutations, et les clients assis à une même table représentent les individus partageant les mêmes gènes. Le numéro de la table représente l'ordre dans lequel ces diverses mutations ont apparu sur l'arbre du coalescent de Kingman. Ce processus est bien connu, nous connaissons en particulier la probabilité que les $n$ premiers individus soient divisés en $k$ ensembles de taille $n_1,\cdots n_k$ dans l'ordre indiqué, grâce à la formule d'échantillonnage d'Ewens [Ewens 1972], qui se prouve par récurrence :

$\displaystyle{p_{n_1,\cdots n_k} = \frac{\theta^k}{\theta(\theta-1) \cdots (\theta-n+1)} \prod_{i=1}^k(n_i-1)!.}$

La distribution des proportions de chacune de ces classes est plus compliquée à décrire, et utilise l'algèbre beta-gamma.

Nous pouvons néanmoins conclure en signalant que le nombre total de génotypes distincts observés dans un coalescent de Kingman à $n$ individus est de l'ordre de $\theta \log n$. En effet, à chaque ajout d'un nouvel individu, celui-ci possède un génotype différent du précédent avec la probabilité $\frac{\theta}{n+\theta}$. On peut alors conclure grâce à des résultats de la théorie des grandes déviations.

Conclusion

Nous avons, tout au long de cet article, exposé un moyen de modéliser la généalogie d'une population à l'aide d'un modèle, le coalescent de Kingman. Nous avons également étudié plusieurs quantités liées à ce modèle, comme l'âge du dernier ancêtre commun, ou le nombre de familles restant lorsque nous remontons assez loin en arrière. Ces quantités ne peuvent pas s'appliquer aux modèles biologiques sans tenir compte des nombreuses hypothèses que nous faisons, comme la constance de la taille de la population ambiante au cours du temps. Mais elles permettent néanmoins de donner des ordres de grandeurs de quantités apparaissant dans l'étude de l'évolution de certaines populations réelles.

La formule d'échantillonnage d'Ewens est en elle-même un résultat très intéressant, car elle représente la manière dont les individus se répartissent les mutations survenues au cours du temps, lorsque celles-ci sont neutres. Ainsi, en étudiant la proportion d'individus possédant telle ou telle mutation d'un gène, si nous observons une répartition différente de celle exprimée dans la formule d'Ewens, nous saurons que ces mutations ne sont pas neutres, et ont un impact sur la descendance des individus. Cette formule permet donc de confirmer ou d'infirmer l'hypothèse selon laquelle une certaine mutation est neutre.

De nombreux raffinements du coalescent de Kingman existent. On peut par exemple autoriser la coagulation simultanée d'un grand nombre d'individus, c'est-à-dire que l'on peut autoriser que certains individus exceptionnels engendrent d'un seul coup une portion non-négligeable de la population totale. On peut également autoriser que plusieurs de ces coagulations simultanées se produisent en même temps. Ces généralisations s'appellent $\Lambda$-coalescents ou processus de coalescence échangeable.

Nous pouvons également autoriser les individus à se déplacer sur une carte de taille finie ou infinie. Dans ce cas, on suppose que les individus sont localisés en certains endroits précis appelés colonies, et qu'un individu passe d'une colonie à l'autre de manière aléatoire. Cette nouvelle composante du problème change de manière radicale le problème posé. En effet, si dans le cas du coalescent de Kingman non-spatial, il existe presque sûrement un ancêtre commun à cette population, lorsqu'on permet aux individus de se déplacer sur un graphe infini, cet ancêtre commun n'existe pas presque sûrement.

Bibliographie

O. Angel, N. Berestycki, and V. Limic. "Global divergence of spatial coalescents". Preprint. En ligne

J. Berestycki, N. Berestycki, and V. Limic. "The coalescent speed of coming down from infnity", Annals of Probabilities, A paraître.

Ewens, W.J. (1972), "The sampling theory of selectively neutral alleles", Theoretical Population Biology, Vol. 3, p. 87-112.

J.F.C. Kingman (1982). "The coalescent. Stochastic Process", Stochastic Processes and Applications, p. 235-248.

J.F.C. Kingman (1982). "On the genealogy of large populations", Journal of Applied Probabilities, p. 23-49.

Généalogie de populations : le coalescent de Kingman