Généalogie de populations : le coalescent de Kingman

Dans l'article nous nous intéressons au nombre de lignées distinctes présentes à l'instant $t$ dans l'arbre généalogique. Dans cet encart, nous allons étudier le nombre de descendants de chacune de ces lignées. Autrement dit, en étudiant un ancêtre à la $t^\textrm{ième}$ génération, quel est la taille de la famille qu'il a engendré. Nous allons obtenir des estimations intéressantes sur nombre de descendants de la lignée la plus prolifique, et de celle ayant le moins de descendants.

Pour les obtenir, nous aurons besoin d'une nouvelle construction du coalescent de Kingman. En effet, dans notre construction actuelle, nous connaissons les "probabilités de transition", c'est-à-dire la façon de passer d'une situation donnée à une autre. Mais celle-ci ne donne pas la loi de la répartition des tailles des familles. Notre plan est de construire un autre processus d'une manière différente, en donnant cette répartition à chaque instant. Nous vérifierons ensuite que ce processus est bien un coalescent de Kingman. Grâce à l'unicité de celui-ci, nous obtiendrons l'égalité entre les deux processus, en particulier la distribution des tailles de familles, qui nous intéresse. Nous allons commencer par une manière de mesurer la taille des partitions de $\mathbb{N}$. Nous nous intéresserons ensuite à la manière de répartir les descendants de $n$ familles. Nous finirons en construisant la suite des partitions apparaissant au cours du temps.

1. Une autre construction du coalescent de Kingman

Nous nous intéressons à une partition de $\mathbb{N}$ en $n$ ensembles. Remarquons pour commencer que l'un d'entre eux au moins est infini. Afin de connaitre leur taille, nous allons essayer de donner un sens à la proportion d'individus dans chacun de ces blocs. Nous souhaitons par exemple que l'ensemble des entiers pairs soit considéré comme ayant une proportion $\frac{1}{2}$, celui contenant les multiples de 3 comme ayant une proportion $\frac{1}{3}$, etc.

Nous définissons ainsi la proportion d'un bloc $B$ de $\mathbb{N}$ :

$\displaystyle{|B| = \lim_{n \to +\infty} \frac{1}{n}|B \cap \{1, \cdots, n \}| \textrm{ si cette limite existe.}}$

Cette limite n'existe pas toujours, et dans ce cas-là, nous noterons $|B|=\partial$, ce qui signifiera que cette quantité n'est pas définie. Par exemple, le bloc $D$ constitué des entiers compris entre $2^{2p}$ et $2^{2p+1}$ pour tout entier $p$ n'a pas de proportion définie. En effet, on a : 

$\displaystyle{\lim_{p \to +\infty}\frac{1}{2^{2p}-1}|D \cap \{1, \cdots, 2^{2p}-1 \}|=\frac{1}{3}}$

$\displaystyle{\lim_{p \to +\infty}\frac{1}{2^{2p+1}-1}|D \cap \{1, \cdots, 2^{2p+1}-1 \}|=\frac{2}{3},}$

donc la suite n'a pas de limite.

Nous allons maintenant donner la procédure inverse : un moyen d'obtenir une partition de $\mathbb{N}$ possédant des proportions fixées. Soient $\{x_1, \cdots , x_n\}$ des valeurs comprises entre $0$ et $1$ telles que $x_1 + \cdots x_n=1$. Nous construisons une partition aléatoire $\Pi$ possédant $n$ blocs de telle manière que le $i^\textrm{ième}$ bloc possède la proportion $x_i$. Pour cela on choisit $(U_n)_{n \in \mathbb{N}}$ une suite de variables aléatoires indépendantes de loi uniforme sur $[0,1[$. L'individu $n$ est placé dans la partition $i$ si la valeur $U_n$ appartient à l'intervalle $[\sum_{j=1}^{i-1} x_j, \sum_{j=1}^i x_j[$. Dans ce cas, la loi des grands nombres assure que la partition $\Pi$ possède les bonnes proportions.

Nous allons maintenant montrer qu'un coalescent de Kingman peut être construit en utilisant cette méthode. Nous prenons deux ensembles de lois uniformes sur $[0,1]$ indépendantes et uniformément distribuées $(U_n)_{n \in \mathbb{N}}$ et $(V_n)_{n \in \mathbb{N}}$. Les variables aléatoires $(U_n)_{n \in \mathbb{N}}$ permettent de former les partitions de $\mathbb{N}$ selon la méthode précédente, et les variables aléatoires $(V_n)_{n \in \mathbb{N}}$ permettent de définir les proportions de la partition aléatoire que nous allons définir.

Pour tout $n \in \mathbb{N}$, on regarde $V_1,\cdots,V_{n-1}$ qui, distribuées sur le segment $[0,1]$ comme formant une subdivision de ce segment en $n$ intervalles. On note $K(n)$ la partition aléatoire de $\mathbb{N}$ construit sur cette subdivision, qui comporte donc $n$ individus.

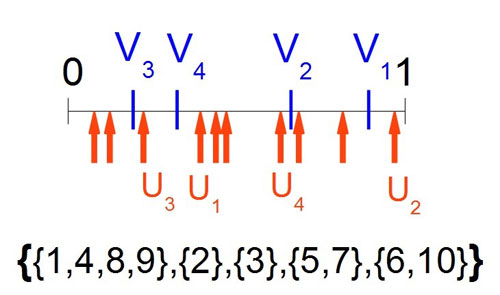Construction sur $[0,1]$ de $K(5)_{|10}$, les dix premiers éléments de la partition de $\mathbb{N}$ en 5 ensembles.

Nous allons maintenant essayer de définir un coalescent de Kingman avec ces quantités. Pour espérer un tel résultat, il faut qu'après un temps exponentiel de paramètre $\frac{n(n-1)}{2}$, on passe du bloc $K(n)$ au bloc $K(n-1)$. Posons donc $D_t$ un processus à valeurs entières défini de la manière suivante : quand $t$ tend vers 0, $D_t$ tend vers l'infini, et en tout instant positif $t$, si $D_t$ est égal à $k$, après un temps exponentiel de paramètre $\frac{k(k-1)}{2}$ $D_t$ diminue d'une unité.

Posons $\Pi'_t=K(D_t)$ pour tout instant $t>0$ et $\Pi'_0$ la partition de $\mathbb{N}$ en singletons. Nous pouvons alors prouver que le processus $(\Pi'_t)_{t \geq 0}$ est aussi un processus coalescent de Kingman. En effet, lors d'un saut de $D_t$, on passe d'un processus $K(n)$ à $K(n-1)$, construit par le retrait au hasard d'une partition. Il se trouve que c'est simplement la coagulation au hasard de deux blocs. Par conséquent, lorsqu'on arrive dans la partition $K(n)$, le processus se comporte comme un coalescent de Kingman. Ceci étant vrai pour tout entier $n$, on obtient en passant à la limite quand $n$ tend vers l'infini que $\Pi'$ est un coalescent de Kingman.

Mais le coalescent de Kingman est unique en loi, par conséquent, tout résultat que nous obtenons sur l'une des deux versions que nous avons construite s'étend aussitôt à l'autre. C'est le cas en particulier de la distribution de la partition $K(n)$, la partition des familles obtenues lorsqu'il ne nous reste que $n$ individus dans le coalescent de Kingman.

2. Taille des familles d'individus

Avec cette nouvelle représentation, il devient aisé de calculer la taille des groupes de cousins. En effet, lorsqu'on arrive à $n$ lignées, les proportions de chacune des fratries sont distribuées comme la taille de la subdivision de $[0,1]$ par une collection de $n$ variables aléatoires uniformes indépendantes. Le problème est que les calculs sur les longueurs des intervalles créés par cette partition sont malaisés. Nous allons donc donner le résultat d'un lemme technique, dont la preuve sera donnée en annexe. Ce lemme donne une représentation permettant de manipuler aisément ces longueurs d'intervalles.

Lemme. Soit $e_1,\cdots e_n$ $n$ variables aléatoires indépendantes de loi exponentielle de paramètre 1 et $\gamma_n=e_1+\cdots +e_n$. La loi de la taille des subdivisions de $[0,1]$ par $n-1$ variables aléatoires indépendantes uniformes est égale à celle de $(\frac{e_1}{\gamma_n},\cdots \frac{e_n}{\gamma_n})$. En d'autres termes, ce jeu de variables aléatoires réalise la même subdivision de $[0,1]$ que les variables aléatoires uniformes.

Démonstration. Ce lemme se prouve par un simple changement de variables, il faut démontrer que pour toute fonction continue bornée $f$, l'espérance de $f$ est égale pour les deux jeux de variables aléatoires. Pour cela, notons tout d'abord que si on pose $x_1,\cdots x_n$ les variables aléatoires donnant les tailles de la subdivision, on a :

$\displaystyle{E(f(x_1,\cdots x_n)) = n!\int_{0 \leq s_1 \leq \cdots \leq s_{n-1} \leq 1} f(s_1, s_2-s_1, \cdots, 1-s_{n-1}) ds_1, \cdots ds_n.}$

En effet, nous réalisons un réarrangement dans l'ordre croissant de $V_1,\cdots V_{n-1}$, il y a $n!$ manières de le faire, ce qui donne bien ce que nous obtenons.
Nous pouvons également écrire :

$\displaystyle{E(f(\frac{e_1}{\gamma_n},\cdots \frac{e_n}{\gamma_n})) = \int_{\mathbb{R}^n} f(\frac{s_1}{s_1+\cdots +s_n}, \cdots \frac{s_n}{s_1+\cdots +s_n}) e^{-s_1-s_2-\cdots -s_n} ds_1\cdots ds_n,}$

ce qui en réalisant le changement de variables $u=s_1+\cdots+s_n$ se réécrit
Nous pouvons également écrire :

$\displaystyle{E(\frac{e_1}{\gamma_n},\cdots \frac{e_n}{\gamma_n}) = \int_{\mathbb{R}} \int_{s_1+\cdots +s_{n-1}\leq u} f(\frac{s_1}{u}, \cdots \frac{s_{n-1}}{u},\frac{u-s_1-\cdots -s_{n-1}}{u}) e^{-u} ds_1\cdots ds_{n-1} du.

On réalise ensuite le changement de variables $v_i=\frac{s_i}{u}$, on obtient  :

$\displaystyle{E(\frac{e_1}{\gamma_n},\cdots \frac{e_n}{\gamma_n}) = \int_{\mathbb{R}} \int_{v_1+\cdots +v_{n-1}\leq 1} f(v_1\cdots v_{n-1},1-v_1+\cdots +v_{n-1})u^{n-1} e^{-u} dv_1\cdots dv_{n-1} du.}$

On réalise alors que $\int_0^{+\infty} u^{n-1}e^{-u} du = n!$ par intégrations par parties successives, et on réalise un dernier changement de variables $s_i-s_{i-1}=v_i$ et on retrouve bien la première espérance. On obtient par conséquent qu'il revient au même de considérer les variables aléatoires $(x_1,\cdots x_n)$ et $(\frac{e_1}{\gamma_n},\cdots \frac{e_n}{\gamma_n})$.

Ce lemme nous permet alors de revoir d'un œil nouveau les proportions de chacun des groupes de parentés dans le coalescent de Kingman lorsque nous avons $n$ lignées restantes. Cette représentation est bien plus agréable à manipuler pour ce qui est du minimum et du maximum. Nous en déduisons en particulier les résultats suivants. On note $A_n$ et $a_n$ respectivement la plus grande et la plus petite proportion d'individus lorsqu'on remonte à $n$ lignées.

On a alors $\lim_{n \to +\infty}n A_n - \ln n = G$ et $\lim_{n \to +\infty}n^2 a_n = e$, où on a posé $G$ une variable aléatoire vérifiant $\mathbb{P}(G \leq x) = \exp(-e^{-x})$ et $e$ une variable aléatoire de loi exponentielle. En d'autres termes, quand $n$ devient grand, la plus grande famille a une taille de l'ordre de $\frac{\ln n+G}{n}$ et la plus petite de l'ordre de $\frac{e}{n^2}$.

En effet, grâce à la représentation en loi exponentielle, nous avons $\gamma_n A_n$ la loi de la plus grande de $n$ variables aléatoires indépendantes et de même loi exponentielle de paramètre 1. Nous avons donc :

$\begin{eqnarray} \mathbb{P}(\gamma_n A_n - \ln n \leq x) & = & \mathbb{P}(\max e_1,\cdots, e_n \leq x +\ln n)\\ & = & \mathbb{P}(e_1 \leq x + \ln n, \cdots e_n \leq x+\ln n)\\ & = & \mathbb{P}(e_1 \leq x + \ln n)^n = \left(1-\frac{e^{-x}}{n}\right)^n. \end{eqnarray}

Grâce à un Lemme précédent, on obtient que $\lim_{n \to +\infty}\gamma_n A_n - \ln n = G$ avec $\mathbb{P}(G \leq x) = \exp(-e^{-x})$. La loi des grands nombres nous garantissant que $\lim_{n \to +\infty}\frac{\gamma_n}{n} = 1$, on obtient donc que $\lim_{n \to +\infty}n A_n - \ln n = G$.

Pour ce qui est de $a_n$, on a de la même manière :

$\begin{eqnarray} \mathbb{P}(n\gamma_n a_n \geq x) & = & \mathbb{P}(\min e_1, \cdots e_n \geq \frac{x}{n})\\ & = & \mathbb{P}(e_1 \geq \frac{x}{n})^n\\ & = & (e^{-\frac{x}{n}})^n = e^{-x}. \end{eqnarray}

On obtient donc que $\lim_{n \to +\infty}n^2 a_n = e$, comme annoncé.

Grâce à l'équivalent en 0 du coalescent de Kingman, nous pouvons également réécrire ce résultat en terme de temps passé et non de nombre de lignées restantes. On note maintenant, si $\Pi$ est un coalescent de Kingman, $M (\Pi_t)$ la taille de la plus grande famille à l'instant $t$ et $m(\Pi_t)$ la taille de la plus petite famille. Nous avons alors :

$\displaystyle{\lim_{t\to 0} \frac{2}{t} M(\Pi_t) + \ln \frac{t}{2}= G \textrm{ et}}$

$\displaystyle{\lim_{t\to 0} \frac{m(\Pi_t)}{t^2} = \frac{e}{4}.}$

Ces estimations peuvent être étendues à d'autres quantités, la taille de la deuxième plus grande famille ou d'autres calculs similaires. L'idée force est ici que nous avons réussi à calculer les tailles des familles, qui n'étaient pas accessibles à première vue, en construisant un autre processus, qui a la même loi que le premier. Utiliser ce double regard nous a permis de répondre à de nouvelles questions. 

Retour au sommaire