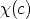Pourquoi les Equations aux dérivées partielles interviennent-elles en biologie?

Par Hatem Zaag, Département de Mathématiques et Applications, ENS

Utiliser les maths en biologie, est-ce efficace ou pas ?

Dans son éditorial à Mathematical slices of molecular biology de A. Carbone et M. Gromov, G. Besson cite (en sortant les paroles de leur contexte) :

1- Wigner qui a écrit un article s'initulant The unreasonable effectiveness of mathematics in the natural sciences [Comm. Pure Appl. Math. 13 (1960), 1-14]

2- Gelfan'd qui a écrit "...the equally unreasonnable ineffectiveness of mathematics in biology".

Alors qui croire ???

Spécificité de la biologie: multiplication et imbrication des niveaux d'organisation et des échelles

La biologie présente une difficulté particulière qu'on ne retrouve pas en physique ou en chimie : Les différents niveaux d'organisation sont multiples et intéragissent trop entre eux.

Quelques niveaux d'organisation/Echelles :

1- Echelle moléculaire et cellulaire: étude de l'ADN et du génome, les propriétés physico-chimiques, la cellule.

2- Echelle de l'organisme: embryologie, développement, morphologie, physiologie (e.g. modélisation du fonctionnement cardiaque, ou de la circulation du sang), relation organe/fonction, comportement, immunologie, cancer.

3. Echelle des communautéss: c'est le domaine de l'écologie, et se ramène souvent à des modèles de dynamique des populations.

Citons un exemple de thématique usuelle de la biologie où différentes échelles interagissent de manière évidente : l'étude d'une maladie virale.

1- Echelle moléculaire et cellulaire: le virus lui-même (qui est une séquence d'ADN) et cellules du système immunitaire.

2- Echelle de l'organisme: organes touchés.

3- Echelle des communautés: contagion.

Deux axes majeurs en Math-Bio

1-Analyse de données, statistiques, probabilités.

2-Modélisation par systèmes dynamiques, équations différentielles ou équations aux dérivées partielles (non linéaires)

Les systèmes dynamiques et les EDPs interviennent à toutes les échelles d'organisation des sciences du vivant.

Un exemple : le chimiotactisme dans le cas de l'amibe Dictyostellium discoideum

... usuellement appelée par un petit nom moins effrayant : "Dicty".

Le chimiotactisme (ou la chimiotaxie) est le mouvement de bactéries, amibes, cellules, sous l'influence d'une substance chimique, le chimioattracteur, que ce soit par attraction (e.g. nourriture) ou répulsion (e.g. poison).

Observons le comportement étrangement agrégatif de Dicty dans certaines circonstances :

Film 1 (source : dictybase.org)
Agrégation d'amibes D. discoideum vers un point source du chimioattracteur cAMP (cyclo Adénosine Monophosphate).
Temps en minutes et secondes.
D'après G. Gerisch, Max Planck Institut für Biochemie, Martinsried, Allemagne.
Film 2 (source : dictybase.org)
Chimiotaxie d'une seule cellule vers un point source de cAMP (cyclo Adénosine Monophosphate).
Temps en minutes et secondes.

D'après G. Gerisch, Max Planck Institut für Biochemie, Martinsried, Allemagne.
Film 3 (source : dictybase.org)
Agrégation d'amibes.
Intervalle de temps entre les étapes: 6 minutes.
D'après P. Devreotes, Johns Hopkins Medical Institutions, Baltimore, Etats-Unis.

L'explication donnée par D. Horstmann est la suivante :

1- D. Discoideum est un organisme unicellulaire qui se reproduit par division cellulaire tant que les ressources du milieu en nourriture sont suffisantes.

2- Lorsque les ressources sont epuisées, les amibes occupent tout l'espace disponible.

3- Une amibe sécrète le chimioattracteur cAMP (cyclo Adénosine Monophosphate), qui attire les autres.

4- Les amibes bougent en direction de l'amibe "fondatrice", et sécrètent le cAMP (cf. Film 3).

5- Agrégation et début de différentiation.

6- Formation d'un pseudoplasmoide (corps multicellulaire de quelques centaines de milliers de cellules!).

7- Le pseudoplasmoide bouge en direction des sources de lumière.

8- Formation d'un corps fructifiant et émission de spores... Le cycle peut alors recommencer (naissance d'amibes...)

Remarque : c'est l'un des rares cas dans la nature où des individus unicellulaires s'unissent pour former un individu multicellaire dans le but de sauver la "communauté".

Intérêt de Dicty pour la recherche médicale

C'est un modèle simple pour l'étude du chimiotactisme, mécanisme qui intervient chez des organismes supérieurs également (différentiation des cellules, cancer, etc...)

Exemple : Angiogénèse autour d'une tumeur cancéreuse

(L'angiogénèse est le processus de fabrication de vaisseaux sanguins.)

Au début, la tumeur puise ses ressources dans le milieu ambiant.

A un certain point de son développement, elle envoie un signal chimique dans le milieu extérieur pour attirer les cellules endothéliales (cellules qui tapissent l'intérieur des vaisseaux sanguins), et ainsi former des vaisseaux sanguins capillaires qui la fournissent en nutriments.

A ce stade, la tumeur commence à être très dangereuse pour le malade car elle est à même de créer des métastases grâce à ces nouveaux vaisseaux créés par chimiotactisme.

Modélisation simplifiée du chimiotactisme

Le chimiotactisme est l'un des sujets étudiés au Département de Mathématiques et Applications de l'ENS. Voir par exemple la note due à L. Corrias (Université d'Evry), B. Perthame (DMA) et l'auteur de ce texte.

Les variables qui interviennent sont les suivantes :

x est la variable d'espace, a priori en 3 dimensions, mais qu'on peut considérer de dimension 1 dans un premier temps pour simplifier (on imagine que les amibes sont distribuées sur une ligne.)

t est le temps.

n(x,t) la densité des amibes en fonction de l'endroit où l'on regarde (x)et du temps (t).

c(x,t) est la densité du signal chimique cAMP.

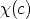$\chi(c)$ mesure la sensibilité de l'amibe au signal chimique.

Evaluons l'accroissement temporel de n(x,t) :

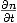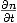$\frac{\partial n}{\partial t}$ est la somme de trois termes : (Pour la définition de $\frac{\partial n}{\partial t}$ , cliquer ici.)

1 - Le terme de diffusion : 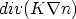$div(K\nabla n)$ . (En savoir plus)

2 - Le terme de division cellulaire 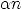$\alpha n$ , en supposant qu'elle est proportionnelle au nombre d'amibes.

3 - le terme de chimiotactisme 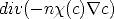$div(-n\chi(c)\nabla c)$ . (En savoir plus)

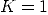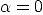Bilan (avec $K=1$ et $\alpha=0$ ) :

$\frac{\partial n}{\partial t}=\Delta n - div(-n\chi(c)\nabla c)$ (En savoir plus)

Comme c est produit par l'amibe elle-même, il vérifie une équation du genre :

$\frac{\partial c}{\partial t}=\Delta c + f(n)~~ (f(n)\geq 0)$ (En savoir plus)

Le signe positif de 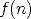$f(n)$ traduit le fait que la substance chimique est créée par les amibes.

Questions intéressantes :

1- Existence et unicité de solutions (et régularité de ces solutions).

2- Comportement asymptotique. Peut on prédire qu'il y aura agrégation en un temps fini ? Peut on décrire la façon dont l'agrégation se fait ? (vitesse ?)

A l'heure actuelle, un seul résultat de comportement asyptotiquea été trouvé, par Herrero, Medina et Velazquez, dans le cas où le problème a une symétrie radiale.

La résolution numérique pose problème en cas d'agrégation car la densité des amibes n(x,t) tend alors vers l'infini, prenant des valeurs très grandes dont la gestion numérique est délicate.

Conclusion

La biologie est un gisement inépuisable de problèmes à modéliser. L'épidémiologie, l'imagerie médicale, la circulation du sang, les modèles cardiaques, le cancer sont des exemples parmi tant d'autres...

Néanmoins, la biologie ne se réduit pas à une simple métaphore de modèles mathématiques. La biologie pose en effet des problèmes spécifiques et non triviaux a la modélisation par des EDP.