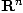 , c'est associer à tout point
, c'est associer à tout point
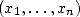 un vecteur
un vecteur 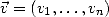 de
de 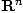 .
.
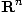 est tout simplement une application de cet espace dans
est tout simplement une application de cet espace dans 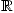 ("on associe à tout point de l'espace une grandeur scalaire".)
("on associe à tout point de l'espace une grandeur scalaire".)
Définir un champ de vecteurs de 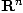 , c'est associer à tout point
, c'est associer à tout point
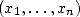 un vecteur
un vecteur 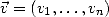 de
de 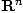 .
.
Physiquement, cela consiste à imaginer que l'espace 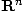 est
empli par un fluide animé par un courant et qu'à chaque point on associe le
vecteur vitesse du courant en ce point.
est
empli par un fluide animé par un courant et qu'à chaque point on associe le
vecteur vitesse du courant en ce point.
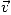 différentiable de
différentiable de 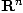 , alors sa divergence est le champ
scalaire défini par
, alors sa divergence est le champ
scalaire défini par
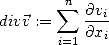
Intuitivement, cet opérateur évalué en un point x permet de dire si le champ de vecteur, au voisinage de x, se rapproche ou s'éloigne de x, en moyenne.
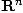 , alors son gradient est le champ de
vecteurs défini par
, alors son gradient est le champ de
vecteurs défini par
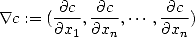
Intuitivement, en voyant le champ c comme la concentration d'un produit dans l'espace, le gradient de c en un point xnous indique la direction vers laquelle, en moyenne, cette concentration augmente.
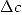 d'un champ scalaire continûment dérivable c
est égal à la divergence de son gradient. C'est donc aussi un champ scalaire.
d'un champ scalaire continûment dérivable c
est égal à la divergence de son gradient. C'est donc aussi un champ scalaire.
Techniquement, il est égal à
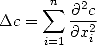
C'est le plus courant des opérateurs d'ordre supérieur à 1,et il apparaît dans des équations aux dérivées partielles importantes (équation de Laplace, équation de la chaleur, etc...).