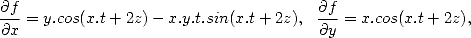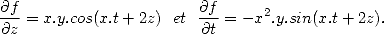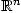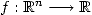Dérivées Partielles

Considérons une fonction $f:\R^n\lra \R$. On voudrait étudier son comportement local.

Si n=1, on peut étudier l'accroissement de f en un point x grâce à f'(x). Cette méthode n'est évidemment plus directement utilisable pour n>1, car on définit la dérivée par une opération de division, qui n'est plus disponible dans 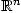$\R^n$ !

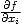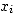On peut cependant définir n dérivées partielles notées $\frac{\partial f}{\partial x_i}$ en s'intéressant à l'accroissement de f lorsque seule $x_i$ varie, les autres variables étant considérées constantes.

Commençons par considérer le cas où n=2.

Dérivées partielles d'une fonction à deux variables

Considérons une fonction 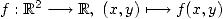$f:\R^2\lra\R,~ (x,y)\lmt f(x,y)$.

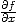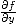On définit la dérivée partielle $\frac{\partial f}{\partial x}$ de f par rapport à x en dérivant f comme une fonction de la seule variable x, y étant considérée comme un paramètre constant. On définit bien entendu $\frac{\partial f}{\partial y}$ de manière analogue.

Exemples : (i) Soit f(x,y)=x+y, alors

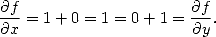
$$\frac{\partial f}{\partial x}=1+0=1=0+1=\frac{\partial f}{\partial y}.$$

(ii) Soit f(x,y)=cos(x)+sin(y), alors

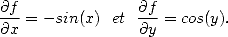
$$ \frac{\partial f}{\partial x}=-sin(x) ~ ~ et~~ \frac{\partial f}{\partial y}=cos(y). $$

(iii) Soit f(x,y)=xy, alors

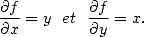
$$ \frac{\partial f}{\partial x}=y ~ ~ et~~ \frac{\partial f}{\partial y}=x. $$

(de la même manière que, si g(t)=2t, alors g'(t)=2.)

(iv) Soit f(x,y)=cos(x).ln(1+y), alors

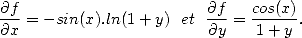
$$ \frac{\partial f}{\partial x}=-sin(x).ln(1+y) ~ ~ et~~ \frac{\partial f}{\partial y}=\frac{cos(x)}{1+y}. $$

(v) Soit f(x,y)=cos(x.y), alors

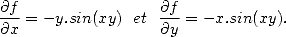
$$ \frac{\partial f}{\partial x}=-y.sin(xy) ~ ~ et~~ \frac{\partial f}{\partial y}=-x.sin(xy). $$

Cas général :

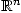Considérons une fonction f de $\R^n$ dans $\R$ :

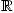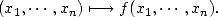
$$ (x_1,\cdots,x_n)\lmt f(x_1,\cdots,x_n). $$

On peut définir exactement comme ci-dessus n dérivées partielles notées 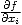$\frac{\partial f}{\partial x_i}$ en dérivant f par rapport à la seule variable 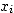$x_i$, les autres variables étant considérées comme des constantes.

Exemples : (i) Soit f(x,y,z,t)=x.y.z.t, alors

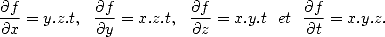
$$ \frac{\partial f}{\partial x}=y.z.t,~~ \frac{\partial f}{\partial y}=x.z.t,~~ \frac{\partial f}{\partial z}=x.y.t~~et~~ \frac{\partial f}{\partial t}=x.y.z. $$

(ii) Soit f(x,y,z,t)=x.y.cos(x.t+2z), alors

$$ \frac{\partial f}{\partial x}=y.cos(x.t+2z) - x.y.t.sin(x.t+2z),~~ \frac{\partial f}{\partial y}=x.cos(x.t+2z),~~ $$

$$\frac{\partial f}{\partial z}=x.y.cos(x.t+2z)~~et~~ \frac{\partial f}{\partial t}=-x^2.y.sin(x.t+2z). $$