Les géomètres de la Grèce antique
Bernard Vitrac
8- Apollonius de Perge et la tradition des coniques
Dans la lettre-dédicace qui accompagne son commentaire aux Coniques d'Apollonius, Eutocius précise :
«Le géomètre Apollonius, mon cher compagnon Anthémius, originaire de Pergè en Pamphylie, a vécu au temps de Ptolémée Évergète comme l'écrit Héracléios, le biographe d'Archimède ».
Le dédicataire est probablement Anthémius de Tralles, co-responsable, avec Isidore de Milet, de la construction de la cathédrale Sainte-Sophie à Constantinople, en 532. Eutocius s'adresse à lui comme à un ami et un condisciple un peu plus jeune. Nous pouvons donc situer son activité scientifique au tournant des Ve-VIe siècles. L'identification de sa source soulève davantage de problème car le texte parle d'un certain Héracléios, auteur d'une vie d'Archimède, alors que dans une de ses œuvres antérieures — son commentaire à la Mesure du cercle d'Archimède — Eutocius se référait à Héraclide, auteur d'une vie d'Archimède !
|
Figure 1 : La
cathédrale Sainte Sophie
  Cathédrale
Sainte Sophie construite à Constantinople sous le
règne de Justinien, entre 532
et 537. Elle fut ultérieurement
transformée en mosquée. Ses architectes furent
Anthémius de Tralles et Isidore
de Milet. C'est au premier qu'Eutocius dédicaça
son commentaire aux quatre
premiers Livres des Coniques d'Apollonius.
Isidore révisa l'édition des Commentaires d'Eutocius au
traité de la Sphère
et du cylindre d'Archimède.
La
coupole s'effondra à la suite d'un tremblement de terre en
558. Elle fut
reconstruite par Isidore le Jeune, neveu du premier. |
Il est fort peu probable qu'il ait
existé deux biographes d'Archimède avec des noms
si proches. Le Syracusain est
d'ailleurs le seul mathématicien grec, non-philosophe,
à qui l'on ait consacré
une biographie. Sans doute s'agit-il donc du même auteur dont
le nom s'est
trouvé altéré. Beaucoup de
spécialistes tranchent en faveur d'Héraclide car
Archimède lui-même rappelle à
Dosithée, dans la lettre-préface du
traité des Spirales, qu'il
lui a fait parvenir
certaines démonstrations dans des livres
qu'Héraclide
lui a remis.
Avec cette identification, le biographe serait un contemporain du
Syracusain,
et même un familier, sans doute un peu plus jeune, que l'on
veut croire bien
informé et digne de foi. Malheureusement, Eutocius poursuit
:
Figure 2 :
Les ruines de la cité de Pergame 
La
cité de Pergame s'est doté d'un magnifique
ensemble architectural au début du
IIe siècle avant notre
ère, sous le règne d'Eumène II
(197-159). Au nord de l'Acropole, au dessus du
théâtre, se trouvait la
Bibliothèque, rivale de celle d'Alexandrie. Elle a
possésé, dit-on, 200 000
rouleaux. Du nom de cette cité dérive le nom grec
"pergamenê" du
parchemin, peau d'animal préparée pour devenir le
support de l'écriture, en
concurrence avec le papyrus, qu'il finira par supplanter.
Grâce aux préfaces
des Livres I et II, nous savons qu'Apollonius vint à Pergame
pour rencontrer
son dédicataire, le géomètre
Eudème de Pergame (à ne pas confondre avec
l'historien Eudème de Rhodes).. |
Une
querelle de priorité
Nous voici en face d'une (prétendue)
querelle de priorité quant à la
paternité des résultats concernant les
coniques. Dans l'autre témoignage
dérivé d'Héraclide
— celui de la préface
du commentaire à la Mesure du
cercle —,
il est affirmé que le but d'Archimède,
dans ce traité, était de fournir une
approximation de ce que nous appelons
aujourd'hui le nombre π « utile pour les besoins de la
vie quotidienne ».
Or, à la fin dudit commentaire, Eutocius nous apprend
incidemment qu'Apollonius
avait proposé un encadrement plus précis que [3
; 3
], mais,
ajoute-t-il en s'inspirant d'Héraclide,
si ce travail était plus précis, il ne
poursuivait pas le même but
qu'Archimède,
à savoir satisfaire les besoins de
la vie quotidienne. Autrement
dit, cette double mention du "besoin" apparaît comme une
clause
défensive, justifiant l'approximation
archimédienne au regard de celle, plus
précise, qu'avait donnée Apollonius. Dans ces
deux exemples, de toute évidence,
Héraclide n'est guère favorable à
l'auteur des Coniques. Cela dit, il n'a
peut-être pas tort de souligner l'émulation, voire
la rivalité au moins
implicite, qui semble prévaloir entre Apollonius et les
mathématiciens
contemporains ou antérieurs à lui, notamment
Archimède.
Dans les préfaces aux différents
Livres des Coniques, Apollonius
souligne abondamment la nouveauté et
l'intérêt de certains résultats,
l'extension, la généralité et la
clarté de son exposé. Celui-ci l'emporte de
beaucoup sur ceux de ses prédécesseurs. Il
critique au passage Euclide
ce qui
n'a pas manqué, là aussi, de susciter quelques
remarques défensives. Dans la
préface du Livre IV, Apollonius atteste d'un
échange un peu vif
entre Conon de Samos — le correspondant et ami
d'Archimède — et un certain
Nicotélès de Cyrène. Dans son
impartiale intransigeance il égratigne les deux
protagonistes. Bref, la gratitude vis-à-vis des
prédécesseurs n'est pas le
sentiment qu'Apollonius exprime le plus aisément.
Au-delà d'hypothétiques
traits de caractère, il faut sans doute évoquer
la "pression" qui
s'exerce sur les géomètres au tournant des IIIe-IIe
siècles.
Si les institutions savantes alexandrines favorisent la recherche et l'émulation, elles n'induisent pas forcément des relations interpersonnelles très sereines. Nous n'en savons rien pour ce qui regarde les sciences mathématiques, mais le poète satiriste Timon de Phlionte s'en fait l'écho pour ce qui concerne les domaines littéraires et philologiques. Sa description du Musée est féroce : « Dans la populeuse terre d'Égypte sont engraissés des gribouilleurs de livres qui passent leur temps à se donner des coups de bec dans la cage des Muses ». Plus sérieusement, Apollonius mène ses recherches après deux générations de géomètres : Aristée, Euclide, Conon, Dosithée, Archimède, Ératosthène, Nicomède, Dioclès … comme peu d'époques en ont connu. Pour se faire connaître, il faut donc se démarquer clairement et mettre en avant l'intérêt et la nouveauté de son travail.
|
||||
Archimède
et Apollonius
Archimède n'est jamais nommé dans
les deux seuls traités conservés d'Apollonius,
mais aux cas déjà mentionnés de
l'approximation du nombre π et de l'étude de la
courbe appelée
"cochlias",
on ajoutera qu'Apollonius avait développé un
système de notations des grands nombres qui
apparaît comme une réponse
différente de celle, plus complexe, proposée par
Archimède dans son Arénaire.
Les
mathématiciens ultérieurs donneront la
préférence au système
des myriades d'Apollonius. Dans le même ordre
d'idées, son traité des Inclinaisons,
qui
appartenait au corpus dit « du Lieu
analysé » (voir
Encart 1),
établissait qu'un certain nombre de
problèmes de
"neusis"
sont en fait des problèmes-plans, résolubles
« à la règle et au
compas ». Ailleurs il proposait aussi des solutions
alternatives à des neuseis
cette fois solides, en termes de sections coniques. Ces
démarches, tout en
clarifiant le statut de certains problèmes,
réduisaient la portée et
l'intérêt
des recherches de Nicomède sur les lignes
conchoïdes. Apollonius développait
donc un programme de recherches et de publications qui, dans bien des
cas,
obligeaient à reconsidérer les travaux de ses
prédécesseurs.
Mais revenons aux sections coniques.
Eutocius entreprend de laver son auteur de l'infamante accusation de
plagiat.
Pour ce faire il donne la parole à trois témoins
: Archimède, Apollonius et le
philosophe et historien stoïcien Géminus de Rhodes.
Le premier ne se
réfère-t-il pas, à plusieurs reprises,
à des Éléments
des coniques, ouvrage
où étaient manifestement établis des
propositions
qu'Archimède utilise, sans les démontrer, dans
certains de ses traités ? Qui
plus est, Apollonius lui-même ne reconnaît-il pas
que ses quatre premiers
Livres représentent un exposé très
amélioré de ce que d'autres avaient
déjà
proposé ? Ne les désigne-t-il pas comme des
livres « d'Éléments
»,
suggérant par
là que ce sont des propositions connues (depuis un certain
temps) pour jouer un
rôle architectonique dans la théorie des sections
coniques ? Eutocius a
incontestablement raison en ce qui concerne Apollonius et la
manière dont il
s'exprime, notamment dans la préface de son premier Livre.
L'assertion relative
à Archimède est plus incertaine car il se
pourrait que le Syracusain renvoie de
cette manière à l'un de ses propres
écrits. Rien ne nous oblige à croire qu'il
se réfère nécessairement à
un auteur antérieur.
Les
premiers Éléments des coniques
Sur ce point, il semble bien que
notre commentateur se soit laissé impressionner par un autre
"historien" de la théorie des coniques, Pappus. La
présentation que
celui-ci consacre au traité d'Apollonius commence ainsi :
« Apollonius
nous a transmis huit livres sur les coniques en ayant
complété les quatre
livres des Coniques
d'Euclide, et y ayant ajouté quatre autres
livres. Aristée, auteur de cinq livres sur Les
lieux solides, encore disponibles aujourd'hui, à
la suite des Coniques,
avait toutefois, comme les
prédécesseurs d'Apollonius, appelé
l'une
des sections coniques la « section de cône
acutangle », l'autre la
« section de cône rectangle » et
l'autre encore, la « section de cône
obtusangle ».
Le texte est
précieux, tout particulièrement pour l'indication
qu'il livre au sujet
d'Aristée et sur la désignation des sections
coniques que celui-ci utilisait,
clairement différente de celle d'Apollonius, laquelle est
encore la nôtre
aujourd'hui (ellipse, parabole, hyperbole). Nous y reviendrons.
Eutocius, à la suite de Pappus,
considérait probablement que les Éléments
des coniques auxquels
se référait
Archimède étaient ceux d'Euclide, l'auteur d'Éléments
(stoïchéiôtês) par excellence
pour les auteurs de
l'Antiquité tardive. Qu'Euclide ait travaillé et
écrit sur les sections
coniques, c'est manifeste d'après le témoignage
d'Apollonius lui-même. Qu'il
ait rédigé quatre Livres
d'éléments sur cette théorie,
qu'Apollonius
se serait contenté de remanier comme l'affirme Pappus, c'est
moins certain. Le
corpus dit « du lieu analysé »
mentionne un ouvrage d'Euclide intitulé Lieux
à la surface, en
deux Livres, lequel, de par sa place dans
le corpus — il vient à la suite des Coniques
d'Apollonius
et des Lieux solides d'Aristée
— ne se limitait pas aux problèmes dits plans
(voir Encart
1). Les travaux qu'Euclide avait consacrés aux
sections coniques se trouvaient
probablement dans cet écrit. En outre, s'il portait sur des
questions
spécifiques, essentiellement des problèmes de
lieux, comme le font la plupart
des ouvrages de ce corpus, l'exposé n'en était
pas nécessairement synthétique,
comme celui d'Apollonius dans le traité des Coniques, mais plutôt
analytique. Rien ne permet non
plus d'affirmer qu'il était limité aux seules
sections coniques parmi les lieux
engendrés par considération de la surface de
certains solides. On peut
d'ailleurs faire les mêmes remarques au sujet des Lieux solides d'Aristée.
Proclus, parmi les œuvres nombreuses qu'il attribue
à Euclide, ne mentionne pas
d'Éléments des coniques.
Quant aux références
archimédiennes
à de tels éléments, elles s'expliquent
autrement. A une exception près, peu
probante, elles renvoient toutes à des résultats
qui figurent dans les Livres I
à IV des Coniques… d'Apollonius,
Livres qu'il désigne lui-même
comme "Éléments”. Ces
références livresques sont donc probablement
inauthentiques et plus tardives. Elles ont été
ajoutées aux écrits d'Archimède
pour faciliter la
tâche du lecteur et, si cette
hypothèse est la
bonne, cela s'est fait après la rédaction des Coniques d'Apollonius,
mais
avant l'époque d'Eutocius qui pouvait les lire. Cela laisse
quand même une
période de 700 ans pour ce faire !
Au bout du compte, l'accusation d'Héraclide telle que la rapporte Eutocius reste une énigme. A moins de supposer que le commentateur ne l'ait pas bien comprise et qu'elle visait un ensemble tout à fait déterminé de propositions concernant les coniques pour lesquelles Archimède aurait anticipé Apollonius. Mais, à un niveau global, Eutocius n'avait aucune raison de douter que ces courbes avaient été étudiées avant ces deux auteurs, notamment par Aristée et Euclide. De fait, dans l'anthologie de solutions pour le problème de l'insertion de deux moyennes proportionnelles entre deux droites données qu'il a réunie dans son commentaire de la Proposition II. 1 de la Sphère et du cylindre d'Archimède, Eutocius nous livre deux autres très précieux témoignages sur l'histoire des sections coniques.
Ménechme,
l'inventeur des
sections coniques ?
D'abord il transmet une solution
attribuée au géomètre
Ménechme de Proconnèse qui montre comment
réaliser ladite
insertion à l'aide d'une parabole et d'une hyperbole.
Ménechme et son frère
Dinostrate sont connus comme disciples
d'Eudoxe de Cnide, contemporains
d'Alexandre le Grand .
Les premières recherches sur ces courbes
remontent donc au moins au milieu du IVe s.
avant J. C. La
désignation des coniques dans ce témoignage est
celle d'Apollonius, autrement
dit notre commentateur (ou sa source) a modernisé
l'expression tout en
conservant la démarche (voir Encart 2).
La
résolution est purement théorique.
Elle présuppose que l'on sache caractériser nos
courbes en termes
de lieux définis par des égalités
d'aires (les conditions (i)-(ii) dans l'encart
2). L'hyperbole équilatère, par
exemple, est le
lieu des points H tels que le
produit de ses distances à deux droites perpendiculaires
données, DF, DK, est
donné. La synthèse exige aussi que l'on
possède un moyen effectif de construire
ou d'engendrer lesdites courbes. Pour qui dispose du traité
d'Apollonius, leurs
constructions sont bien connues, mais qu'en était-il
exactement pour Ménechme ?
Savait-il que les conditions (i)-(ii) caractérisaient deux
sections du
cône ? Sinon, comment les construisait-il ? Celles-ci
furent-elles découvertes
à l'occasion de ces investigations sur le
problème des deux moyennes comme le
croient certains historiens modernes ? Ou bien étaient-elles
déjà disponibles
pour Ménechme? Il faut alors supposer qu'elles avaient
été introduites dans le
champ de la géométrie pour une autre
problématique, par exemple optique ou
gnomonique. Sur tous ces points Eutocius ne nous dit rien.
Nous possédons, toujours grâce
à
Eutocius, un second élément d'information sur le
travail de Ménechme. Nous
avions dit que le commentateur recopie l'épigramme
d'Ératosthène accompagnant
la dédicace de son mésolabe.
Pour vanter
l'effectivité de sa
solution et critiquer celles de ses
prédécesseurs, ce dernier invite le lecteur
qui passe devant l'inscription à
« renoncer à tenter les laborieux travaux
d'Archytas au moyen de cylindres, ou à couper le
cône selon les triades de Ménechme,
ou à décrire la forme courbe dans les lignes
comme l'a fait le divin Eudoxe ».
A sa manière le savant Bibliothécaire confirme
l'invention, par Ménechme, de la
solution que nous avons précédemment
décrite. Il est clair qu'Ératosthène
sait
que les courbes utilisées peuvent êtres
engendrées comme sections du cône et on
peut penser qu'il attribue ce savoir à l'inventeur. Est-il
poétiquement
anachronique ? L'expression « triades de
Ménechme » est assez
énigmatique.
On la retrouve chez Proclus. Certains pensent qu'il s'agit simplement
des trois
courbes, deux paraboles et une hyperbole, qui se trouvent directement
associées
à sa procédure de résolution, d'autres
qu'il s'agit des trois espèces
principales des sections coniques : ellipse, parabole, hyperbole.
La génération des coniques selon Aristée
Si la manière dont Ménechme
construisait ces courbes nous échappe, reste la fin du
témoignage de Pappus et
ce qu'Eutocius reprend à Géminus de Rhodes. Dans
chaque cas, il s'agit
d'opposer deux manières d'engendrer les coniques comme
sections du cône,
l'ancienne et la nouvelle. Nos auteurs rapportent la
première à Aristée dit
l'ancien, la seconde à Apollonius lui-même. Ces
deux modes d'engendrement sont
censés justifier deux façons de
désigner les courbes. Géminus faisait d'abord
remarquer que les Anciens définissent le cône
comme la figure engendrée par la
révolution d'un triangle rectangle autour de l'un des
côtés de son angle droit.
Tous les cônes définis de cette manière
sont donc droits ou, pour le dire
autrement, l'axe du cône est perpendiculaire au plan de sa
base. Ceci
correspond effectivement à ce que l'on trouve dans les
définitions du Livre XI
des Éléments d'Euclide qui distinguaient
ensuite trois
espèces de cônes dits respectivement "rectangle",
"acutangle", "obtusangle" (Cf. Figure 4).
|
||||||||||||
|
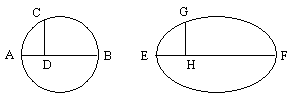
Figure
5: Les coniques selon Aristée
 |
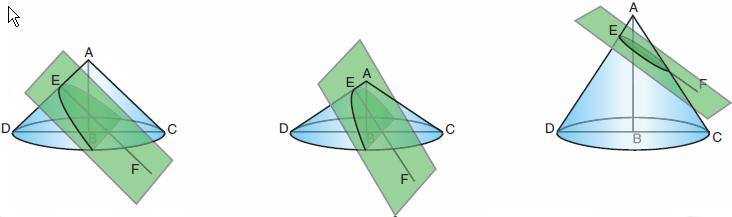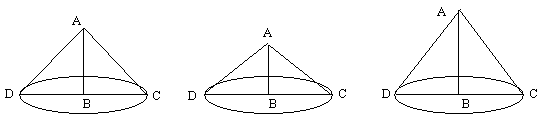
On voit
immédiatement que :
• dans le
cône
rectangle, EF sera parallèle à AC;
• dans le
cône
obtusangle, EF s'écarte de AC (mais si on la prolongeait de
l'autre côté de AD,
elle couperait CA prolongée au-delà de A).
• dans le
cône
acutangle, EF coupera AC (ou son prolongement).
Dans les deux
premiers cas, les sections sont infinies, mais, dans le
troisième, on obtient
une sorte d'ovale parfaitement déterminé.
|
||||
L'approche d'Apollonius
Il suffit d'ouvrir
le premier Livre des Coniques d'Apollonius
pour
comprendre que sa perspective n'est pas la même, qu'il
cherche
à atteindre un
très haut degré de
généralité.
Déjà sa première définition
introduit, non
pas
le cône, mais la surface conique, décrite de la
manière suivante :
«
Si, d'un certain point, l'on mène à une
circonférence de cercle non située dans
le même plan que ce point, une droite prolongée de
part et d'autre, et si, le
point restant fixe, la droite se trouve portée selon la
circonférence jusqu'à
ce qu'elle reprenne la position d'où elle avait
commencé de se mouvoir,
j'appelle « surface conique » celle qui,
décrite par la droite, est composée de
deux surfaces opposées par le sommet …
».
D'une part la
surface conique possède deux "nappes", opposées
par le sommet,
d'autre part, si on la coupe par un plan pour engendrer un
cône, celui-ci, en
toute généralité, pourra
être droit ou oblique. Les définitions 4
à 8 sont
encore plus déroutantes pour un lecteur qui ignorerait tout
des sections
coniques. Pour toute courbe plane, Apollonius appelle
"diamètre" une
droite qui, menée à l'intérieur de la
courbe, coupe en deux parties égales tous
les segments de droite menés à
l'intérieur de la courbe parallèlement
à une
droite quelconque ! Ces parallèles sont
elles-mêmes appelées « droites
menées de manière ordonnée »
(d'où nos "ordonnées"). Il introduit des
notions similaires pour deux courbes coplanaires. Est-ce que de telles
choses
existent avec un tel degré de
généralité ? Pourquoi
considérer deux
courbes coplanaires ? Les réponses viendront
plus tard.
|
||||||
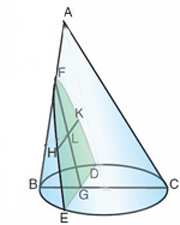
Quant à la "mystérieuse"
notion de diamètre d'une courbe quelconque, sa pertinence
est rapidement
justifiée, dès la Proposition 7. La situation est
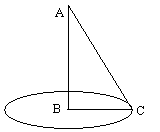
la suivante (voir Encart
5)
:
on coupe un cône quelconque de sommet A ayant le cercle de
diamètre BC comme
base par deux plans, l'un passant par l'axe du cône, comme
ABC, l'autre coupant
la génératrice AB en F et la base du
cône selon une droite DE, de telle manière
qu'elle soit perpendiculaire au diamètre BC ou à
son prolongement. Le premier
plan découpe un triangle ABC (on l'appellera "triangle
axial"), le
second une section conique telle que DFE. Posons que l'intersection du
second
plan avec le triangle ABC est la droite FG. Évidemment trois
cas de figure
peuvent se présenter selon la droite FG est
parallèle à AC, sécante avec elle
ou avec son prolongement (Voir Figure 8).
|
||||||
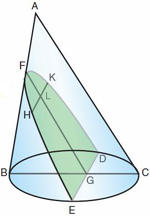
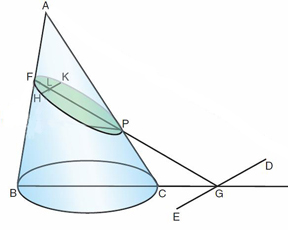
Apollonius montre
que si l'on prend un
point H quelconque sur la section DFE, et ce quel que soit le cas de
figure, et
si on mène la parallèle à DE issue de
H jusqu'au point K sur la section, la
droite FG bissecte la droite HK. Si le cône est droit, FG est
même
perpendiculaire à HK (et DE), mais ce n'est pas
nécessairement le cas si le cône
est oblique (il faut que le triangle axial choisi soit perpendiculaire
à la
base du cône). Quoi qu'il en soit, dans tous les cas de
figure, la droite FG
est un diamètre de la section conique DFE pour des
ordonnées menées dans la
direction de DE. Si elle est perpendiculaire à la direction
des ordonnées,
Apollonius l'appelle "axe" de la section conique.
|
||||
|
|