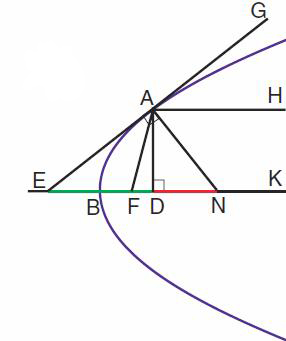
Dossier de Bernard Vitrac sur les géomètres de la Grèce antique - Chapitre 8 : Apollonius de Perge et la tradition des coniques

Encart 4: Le miroir parabolique


Soit une parabole de sommet B et d'axe BK. On mène en A la tangente EAG qui coupe l'axe en E. On mène AN et AD perpendiculaires respectivement à EG et BK. AN s'appelle la normale en A, ED la sous-tangente et DN la sous-normale.


On montre :

(i) que EG est tangente en A si et seulement si EB = BD (la sous-tangente est double de l'abscisse). En fait cette propriété permet de construire facilement la tangente à la parabole en chacun de ses points.

(ii) Que la sous-normale DN est constante, autrement dit indépendante du choix de A.

On introduit F, milieu de EN. On montre très facilement que DN = 2BF, et donc, grâce à (ii), BF ne dépend pas du choix de A. On dit que F est le foyer de la parabole pour la raison suivante : si on mène une droite AH parallèle à l'axe BK, on montre que les angles HAG et EAF sont égaux.

Autrement dit, des rayons solaires incidents parallèles à l'axe se réfléchissent sur la parabole considérée comme un miroir selon des droites, telle AF, qui passent toutes par F.
Retour à l'article

Retour au sommaire