Dossier de Bernard Vitrac sur les
géomètres de la Grèce antique
- Chapitre 8 : Apollonius de Perge et la tradition des coniques
Encart 5: Les coniques selon Apollonius
On coupe un cône quelconque de sommet A ayant le cercle de
diamètre BC comme
base par deux plans, l'un passant par l'axe du cône, comme
ABC, l'autre coupant
la génératrice AB en F et la base du
cône selon une droite DE, de telle manière
qu'elle soit perpendiculaire au diamètre BC ou à
son prolongement. Le premier
plan découpe un triangle ABC (on l'appellera "triangle
axial"), le
second une section conique telle que DFE.
Posons que l'intersection du
second
plan avec le triangle ABC est la droite FG.
Évidemment trois
cas de figure
peuvent se présenter selon la droite FG est
parallèle à AC, sécante avec elle
ou avec son prolongement.
| Figure 1: Cas où FG est parallèle à AC |
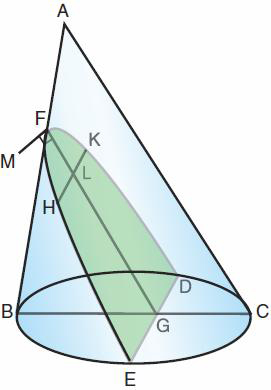 |
La droite FM est perpendiculaire à FG et donnée en longueur
de telle manière que l'on ait
FM : FA :: BC² : BA.AC.
On l'appelle le paramètre de la section. Apollonius montre
que, pour tout point H, on a HL² = FM.FL.
Dans ce cas le résultat n'est pas si différent par rapport à celui de
l 'encart 3a.
Seule la valeur du paramètre FM est plus complexe (c'était AE).
|
| Figure 2: Cas où FG est sécante avec AC |
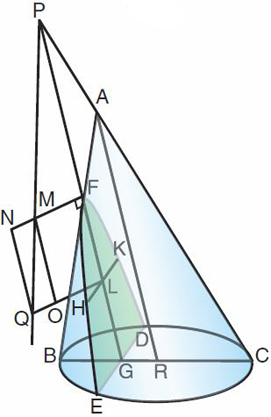 |
On mène AR parallèle à FG. FM est encore perpendiculaire à
FG et donnée en longueur de telle manière que l'on ait
FP : FM :: AR² : BR.RC.
On mène aussi LOQ parallèle à FM.
PM est prolongée jusqu'en Q.
On
complète le rectangle FNQL et on mène MO parallèle à FL.
|
| Figure 3: Cas où FG est sécante avec le prolongement de AC |
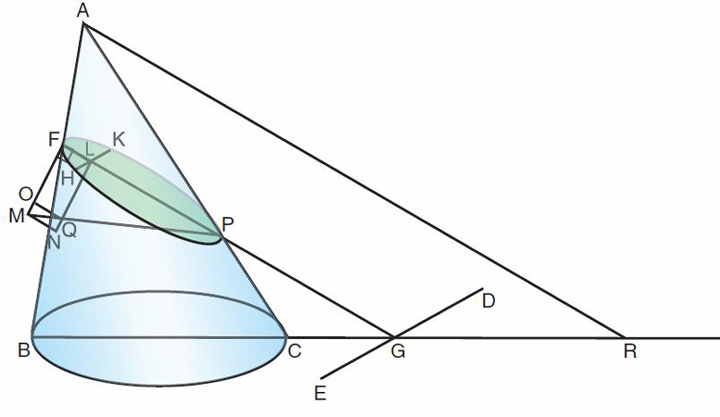 |
On mène AR parallèle à FG. FM est encore
perpendiculaire à FG et donnée en longueur de telle manière que l'on ait
FG :
FM :: AR² : BR.RC.
On joint PM et on mène LQN parallèle à
FM. On complète le rectangle FMNL. On mène QO parallèle à FO.
|
Dans les cas des figures 2 et 3 Apollonius établit
que, pour tout point H, le carré sur l'ordonnée HL est égal à un rectangle,
FNQL (Figure 2), FOQL (Figure 3) qui ont l'un et l'autre comme largeur FL (ce
que nous appelons l'abscisse, c'est-à-dire la portion du diamètre découpée par
l'ordonnée). Selon la terminologie consacrée, on dit que FNQL est appliqué sur
la droite FM avec la figure MOQN en excès, laquelle est semblable au rectangle
contenu par PF, FM (donc à un rectangle donné), tandis que FOQL est dit
appliqué sur la droite FM avec la figure MOQN en défaut, laquelle est semblable
au rectangle contenu par FG, FM, lui aussi rectangle donné).


