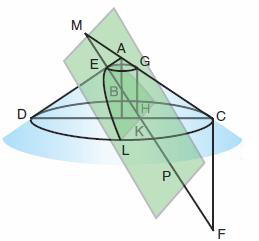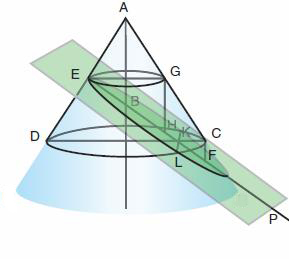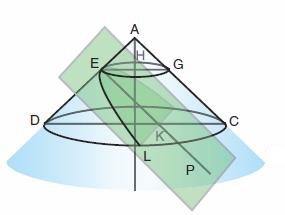
Supposons d'abord le cône obtusangle. On mène par E, situé sur la génératrice AD, un plan perpendiculaire à AD. 

La droite EP est l'intersection de ce plan avec le plan méridien du cône DAC. PE prolongée coupe CA prolongée en M.

Soit K un point quelconque de EP.

Par K et E on mène des plans parallèles à la base du cône; leurs sections avec le cône sont des cercles dont DC et EG respectivement sont des diamètres.

Soit B l'intersection de l'axe avec EP. On mène les perpendiculaires à EG en G et à DC en C. Elles coupent EP en H et F respectivement.

Ce point L est donc sur la surface du cône et dans le plan perpendiculaire à AD. Autrement dit L est un point de la section de cône obtusangle.

Dans le cercle de diamètre DC on a : KL² = DK.KC.

Les triangles rectangles EKD et CKF sont équiangles donc semblables. D'où : EK : KD :: CK : KF. Donc EK.KF = DK.KC. Et donc KL² = EK.KF.

Grâce aux parallélismes, on a FK : HE :: CK : GE :: MK : ME, d'où  FK : MK :: HE : ME.

Or FK : MK :: EK.FK : EK.MK. D'où : EK.FK : EK.MK :: HE : ME :: 2EB : ME.

Les droites BE, EM ne dépendent pas du point K choisi mais seulement de la position du plan sécant. Le rapport 2EB : ME est donc un rapport donné. En termes anciens on dira que le rapport entre le carré décrit sur l'ordonnée KL et le rectangle contenu par les droites découpées par l'ordonnée sur l'axe de la courbe, EK et MK, est un rapport donné.

En notations modernes, on pose y = KL, x₁ = EK, x₂ = MK, EM = a et EB = p (la distance entre le sommet de la section et l'axe du cône). Le fait que L appartient à la section conique se traduit :   y² : x₁x₂ :: 2p : a.

Ce qui est encore plus remarquable, c'est que le symptoma de la section de cône acutangle est exactement le même, étant entendu que le point M est maintenant du même côté que C par rapport à A (c'est toujours l'intersection de EP avec l'autre génératrice, AC).

On pose y = KL, x₁ = EK, x₂ = MK, EM = a et EB = p. Le lecteur peut vérifier que L appartient à la section de cône acutangle si