Dossier de Bernard Vitrac sur les géomètres de la Grèce antique - Chapitre 7 : Archimède

 Encart 3 : « Ce qui fait défaut, c'est la méthode ! »

Les mathématiciens de la Renaissance et de l'Âge classique étaient convaincus que les anciens géomètres disposaient de méthodes heuristiques qu'ils s'ingéniaient à cacher, se contentant de publier leurs démonstrations synthétiques. Dans le cas d'Archimède et de ses preuves par "exhaustion", il fallait qu'il eût, par avance, une idée du résultat à établir. De fait, celui-ci disposait d'une puissante méthode, combinant des considérations mécaniques (loi du levier et détermination des centres de gravité) avec le "découpage" des figures en composants "indivisés" mais déplaçables. Au XVIIe s. on les appelait "indivisibles". A titre d'exemple (simplifié), voyons comment Archimède découvrit que toute sphère est quadruple du cône ayant pour base le grand cercle de ladite sphère et comme hauteur le rayon de la sphère. La figure ci-dessous doit être interprétée comme la section plane d'une figure en trois dimensions.

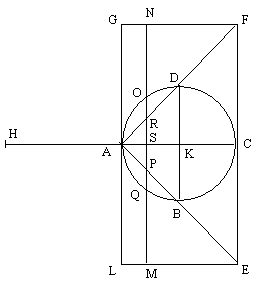ABCD est le grand cercle d'une sphère de centre K.

AC et DB sont deux diamètres perpendiculaires.

Le triangle ADB est la trace, sur le plan de la page, d'un cône de sommet A dont la base est le cercle de diamètre BD, perpendiculaire au plan de la page.

De même AEF est la trace d'un cône de sommet A dont la base est le cercle de diamètre EF.

Il s'agit de montrer que la sphère de centre K et de rayon KA est quadruple du cône ADB.

La droite MN est la trace d'un plan arbitraire perpendiculaire à l'axe AC. Ce plan coupe donc les trois solides, le cylindre selon un cercle de diamètre MN, la sphère selon un cercle de diamètre OQ, le cône AEF selon un cercle de diamètre RP, cercles concentriques dont le centre S appartient à l'axe AC.



Outre les grandes idées de sa méthode, Archimède n'utilise ici que des résultats géométriques très élémentaires, dont certains sont contenus dans les Éléments d'Euclide, par exemple le théorème de l'hypoténuse (I. 47) et le fait que le rapport de deux cercles est le même que celui des carrés décrits sur leurs diamètres (XII. 2). Deux autres propriétés simples de géométrie plane, également dérivables des Éléments sont mobilisées :


 

1. Le rapport de deux droites, AB : AC est le même que le rapport entre le carré sur AB, ABFD et le rectangle qu'elles contiennent ABEC (cf. Eucl., VI. 1).

Ici Archimède utilisera :

MS : SP :: MS2 : MS.SP   (*)

 

2. Le triangle inscrit dans un demi-cercle, tel AQC, est rectangle en Q (Eucl., III. 31).

  

Si l'on mène la hauteur QS, elle découpe des triangles QSA, QSC semblables à AQC (Eucl. VI. 8).

On a donc :

AC : AQ :: AQ : AS. D'où AQ2 = AC.AS   (**)


Partons de l'égalité AQ 2 = AC.AS. Grâce aux symétries de la figure, on voit que, par construction, les triangles ABD, AEF sont des demi carrés. D'où des égalités évidentes :

(i) AS = SP = SR; (ii) AC = CE = AL = MS = SN …

Et donc AC.AS = MS.SP. D'où : AQ2 = MS.SP. Or AQ2 = AS2 + SQ2 (I. 47). D'où AS2 + SQ2 = MS.SP.

Grâce aux égalités (i-ii) on a aussi : AC : AS :: MS : SP. Mais MS : SP :: MS2 : MS.SP (d'après (*)).

D'où :                                      AC : AS :: MS2 : MS.SP :: MS2 : AS2 + SQ2

En remplaçant AS par SP qui lui est égal, puis en prenant les doubles de chacun des segments MS, AS, SQ, on obtient :   AC : AS :: MN2 : PR2 + OQ2.

Jusqu'ici nous avons procédé synthétiquement, un peu à l'"aveugle", mais en n'utilisant que des résultats extrêmement simples. Il faut maintenant nous souvenir que les segments MN, RP et OQ sont les diamètres des trois intersections du plan arbitraire perpendiculaire à l'axe AC avec les trois solides. 

Grâce à la proposition XII. 2, nous déduisons donc une nouvelle proportion :

AC : AS :: cercle de diamètre MN : cercle de diamètre PR + cercle de diamètre OQ.

C'est maintenant qu'interviennent les ingrédients proprement dits de la "méthode". Archimède introduit le point H tel que AH = AC et conçoit la droite HC comme un levier. En remplaçant AC par AH il obtient :

AH : AS :: cercle de diamètre MN : cercle de diamètre PR + cercle de diamètre OQ   (***),

qu'il interprète "mécaniquement". La proportion ci-dessus signifie que si l'on imagine le cercle de diamètre MN (un disque très fin ?) placé en S et les cercles de diamètres PR, OQ placés en H, il y a équilibre.

En effet, selon la loi du levier (démontrée par Archimède dans les Propositions 6-7 de ses Équilibres-plans ), des poids s'équilibrent s'ils sont placés de telle manière que les distances au point de suspension (ici A) sont inversement proportionnelles aux poids. Le Syracusain assimile donc les trois cercles en question à des éléments pesants homogènes (pour que les poids soient proportionnels aux surfaces).
Deuxième grande idée : cet équilibre vaudra quel que soit le plan que l'on a mené tel MN, perpendiculairement à AC. Mais alors, si on les considère "tous", l'ensemble des cercles de diamètre MN (re)constitue le cylindre EFGL, l'ensemble des cercles de diamètre PR constitue le cône AEF, l'ensemble des cercles de diamètre OQ constitue la sphère. Si l'on admet les mêmes opérations de déplacement de ces sortes d'"indivisibles" que sont nos trois espèces de cercle, cela revient à dire que nous suspendons la sphère et le cône au point H. Quant au cercle de diamètre MN, par définition il est de centre S, donc nous ne le déplaçons pas. L'ensemble de ces cercles type MN forme le cylindre EFGL là où il est, autrement dit autour de son centre de gravité, le point K.
Pour le dire autrement, en considérant une infinité (non dénombrable) de proportions de type (***), Archimède affirme que la sphère et le cône, suspendus en H, équilibre le cylindre placé en K :

 

 


Mais AH est le double de AK. Donc, toujours d'après la loi du levier, le cylindre est le double de la somme de la sphère et du cône AEF. Or le cylindre EFGL est triple de ce cône d'après le résultat d'Eudoxe. Donc, par différence, le cône AEF est double de la sphère.

Si on veut revenir au cône inscrit dans l'hémisphère, ABD, on observera que le diamètre de la base du cône AEF est le double de celui de la base de ABD et que sa hauteur, AC, est double de AK. Donc le cône AEF vaut huit fois le cône ABD. On en déduit que la sphère est bien le quadruple du cône ABD, dont la base, le cercle de diamètre BD, est bien un grand cercle de la sphère et dont la hauteur, AK, est le diamètre de la sphère.

Archimède était persuadé que sa démarche pouvait permettre de trouver bien d'autres résultats. C'est pourquoi il rédigea un ensemble d'exemples d'utilisations de cette démarche, accompagné d'une très intéressante lettre-préface. Il expédia le tout à celui qui devait être alors le troisième Bibliothécaire d'Alexandrie, d'où le titre que l'on donne parfois à ce recueil, unique en son genre, de Méthode à Ératosthène. Notre exemple est tiré de la Proposition 2 de ce traité. Malheureusement il connut une transmission chaotique. Longtemps considéré comme perdu (quoique cité par Héron), il ne fut retrouvé qu'à la fin du XIXe siècle !

Retour à l'article