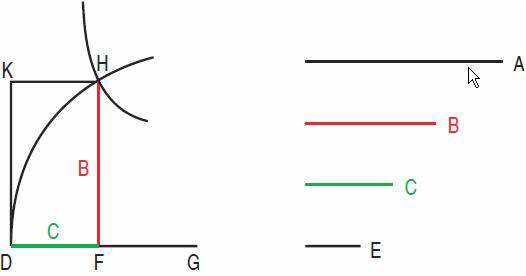
Prenons un point D et, sur une droite DG issue de D, portons DF égale à C.
Élevons la perpendiculaire en F à DG sur laquelle on porte FH égale à B.
Alors (i) signifie que le point H appartient à une parabole de sommet D, définie par la droite donnée A, appelée « côté droit » de la parabole et (ii) revient à dire que ce même point H appartient à une hyperbole (équilatère) d'asymptotes DF, DK, en appelant DK la parallèle à FH issue de D.Si donc on suppose le problème résolu, le point H ainsi construit est l'intersection de deux courbes, une parabole et une hyperbole, et les deux moyennes cherchées, B, C ne sont autres que les droites HF, FD (= HK). Nous venons de décrire ce que les Anciens appelaient une analyse.
Pour résoudre le problème, il faudra donc procéder en sens inverse. Pour cela il faut savoir construire une parabole et une hyperbole dont certaines caractéristiques sont connues, le sommet D et le côté droit, A, pour la parabole, les asymptotes DF, DK, et l'aire égale au rectangle contenu par A et E (ou, si l'on préfère, l'un des points de la courbe) pour l'hyperbole. Leur point d'intersection H déterminera les droites solutions HF, FD. Telle est la synthèse.