CultureMath
Cet article évoque quelques uns des artistes et mathématiciens qui ont transformé une invention d'architecte, la perspective centrale, en une théorie mathématique révolutionnaire, la géométrie projective. Il s'agit d'une brève introduction au livre Douce Perspective. Une histoire d’art et de science de Denis Favennec en collaboration avec Emmanuel Riboulet-Deyris.
Cet ouvrage répond au besoin des physiciens, scientifiques, ingénieurs qui doivent résoudre des problèmes mathématiques dans l'analyse et l'interprétation de phénomènes physiques et de leurs applications techniques. Une première partie, assez élémentaire, traite les équations différentielles, les fonctions analytiques et l'intégration dans le plan complexe, le calcul opérationnel (transformation de Laplace), l'analyse de Fourier et la résolution de quelques équations aux dérivées partielles...
Les 15 problèmes de géométrie de la règle publiés en 1774 par Jean-Henri Lambert ont joué un rôle majeur dans le développement et la diffusion de la perspective, et certains d'entre eux sont encore aujourd'hui des classiques de l'enseignement de la géométrie. Ce dossier présente J.-H. Lambert et son oeuvre mathématique, ainsi que des extraits de son ouvrage "Notes et additions à la perspective affranchie de l'embarras du plan géométral", traduit de l'allemand par J. Peiffer, annoté par R. Laurent et J. Peiffer, et publié en annexe de "La place de J-H. Lambert (1728-1777) dans l'histoire de la perspective" de R. Laurent (cedic: 1987).
‘Les écritures mayas du nombre’ sont une synthèse des plus récents résultats d’analyses épigraphiques et linguistiques du corpus des écritures numérales et numériques réalisées par les scribes mayas depuis l’époque préclassique jusqu’à celle de la conquête espagnole. Interprétées dans le cadre des numérations parlées (de types protractif et additif) et dans celui des mesures de temps, la grande diversité des données analysées conduit à une typologie de l’ensemble des formes (notamment des zéros) et des systèmes mayas d’écriture du nombre, tant dans la représentation des dates et des petites durées, que dans celle des translations temporelles et des grandes durées.
L'histoire de la gestation de la géométrie, c'est-à-dire de sa vie embryonnaire depuis les débuts de la préhistoire humaine jusqu'à sa naissance proprement dite en Grèce antique, n'a jamais été abordée dans son ensemble. Dans cet ouvrage, consacré au Paléolithique et au monde des chasseurs-cueilleurs, l'auteur propose un voyage en compagnie des tailleurs d'outils de pierre qui ont imposé durant plus de deux millions d'années une régularité préconçue à une matière brute, en structurant progressivement leur espace de travail suivant ses trois dimensions...
Dans ce livre, qui vient à la suite de Aux origines de la géométrie. Le Paléolithique et le monde des chasseurs-cueilleurs (Vuibert, 2004), l'auteur cherche à montrer comment, au travers des pratiques rituelles des premiers sédentaires du Néolithique, pratiques dont on peut restaurer la logique grâce à l'ethnographie de certains peuples paysans sans écriture contemporains (Dogons et Banbaras, Navajos), on peut discerner l'apparition d'un schéma du monde et d'un monde des figures...
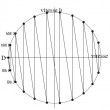
En 1952, dans le commerce des jouets, quand celui ci proposait des objets instructifs et éveillant questions et imagination, humour et habileté manuelle (Wondergraph, père la colique, etc), -contrairement à notre période où les jeux se réduisent à des peluches ou des touches de commande életronique-, une petite toupie en plastique faisait fureur chez les enfants et les adultes d'esprit jeune. Il s'agissait d'une toupie appelée Tippe-Top, de révolution, constituée de deux parties: l'une était une calotte sphérique d'axe z'z, et l'autre un cylindre d'axe z'z emmanché perpendiculairement au plan de la calotte sphérique, l'ensemble formant un seul solide.
Il s'agit d'un surprenant problème de collision qui a fait l'objet du "problème du mois" d'avril 2007: se présentant comme de la mécanique, il se révèle être un moyen (peu efficace!) de calculer Pi. La solution peut être obtenue par des méthodes géométriques ou algébriques.
En 79 diapositives commentées, ce document retrace l'histoire de la géométrie depuis ses origines mésopotamienne, égyptienne et grecque jusqu'aux théories non euclidiennes élaborées au XIXe siècle. Une première partie traite de l'élaboration de la géométrie comme science mathématique, une deuxième partie aborde les géométries non euclidiennes et introduit à une nouvelle conception de la géométrie. Plus qu'une simple histoire, il s'agit d'une réflexion épistémologique sur le rapport entre mathématique et réalité, qui intéressera aussi bien les philosophes que les mathématiciens.
Ce diaporama a été élaboré en Terminale scientifique à la demande conjointe d’Élisabeth ARBOGAST, professeur de mathématiques et Nafissa HAIDAR, professeur de philosophie, toutes deux au lycée Ribeaupierre de Ribeauvillé (Haut-Rhin). Au départ, Mme Haidar avait souhaité un exposé sur la géométrie non euclidienne et à partir de là, aborder les questions d’épistémologie au programme de la classe de Terminale Scientifique. Très vite, nous nous sommes mis d’accord sur l’objectif suivant : mettre en mouvement une dynamique de réflexion qui rompe avec le cloisonnement disciplinaire, et qui amène les élèves à se dire lorsqu’ils font des mathématiques : quel est le sens de ce que je fais en mathématiques ? En quoi est-ce une science exacte ? Comment s’est–elle construite ? Quel lien avec ce que je fais en philosophie ? Et lorsqu’ils sont en cours de philosophie : quels exemples puis-je tirer de mes autres apprentissages, mathématiques, physique, SVT, etc. pour donner corps aux concepts philosophiques, pour illustrer des thèmes comme intuition, évidence, vérité, rigueur, imagination, réalité ?