CultureMath
Les Coniques d’Apollonius de Perge constituent l’un des sommets de la géométrie grecque ancienne. Rédigé, après un premier essai, en huit Livres, leur destinée fut cependant moins heureuse que celle des Éléments d’Euclide. Seuls les quatre premiers Livres — selon l’auteur ils exposent les “éléments” de la théorie — ont été conservés en grec, dans la réédition qu’en procura, à la charnière des Ve et VIe siècles de notre ère, Eutocius d’Ascalon. Les Livres V-VII furent préservés grâce à la traduction arabe qu’en fit Thâbit ibn Qurra mais ils restèrent inaccessibles et excitèrent l’imagination des mathématiciens d’Occident pendant plusieurs siècles.
Dès l’Antiquité, la rigueur et la généralité du traitement apollinien avait été reconnues et avait fait disparaître les écrits antérieurs. Seules quelques bribes d’information, quelques conjectures hasardeuses concernant la découverte des coniques nous ont été transmises par Pappus et Eutocius.
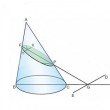
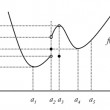
On coupe un cône quelconque de sommet A ayant le cercle de diamètre BC comme base par deux plans, l'un passant par l'axe du cône, comme ABC, l'autre coupant la génératrice AB en F et la base du cône selon une droite DE, de telle manière qu'elle soit perpendiculaire au diamètre BC ou à son prolongement...
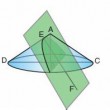
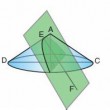
On mène par E, situé sur la génératrice AD, un plan perpendiculaire à AD. La droite EP est l'intersection de ce plan avec le plan méridien du cône DAC. Soit K un point quelconque de EP...
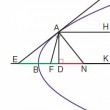
Soit une parabole de sommet B et d'axe BK. On mène en A la tangente EAG qui coupe l'axe en E. On mène AN et AD perpendiculaires respectivement à EG et BK. AN s'appelle la normale en A, ED la sous-tangente et DN la sous-normale...
Le Livre VII de la Collection mathématique de Pappus d'Alexandrie se présente comme un companion destiné à faciliter la lecture d'un corpus de textes, dit « du Lieu analysé », composé de douze traités dus à quatre auteurs...
On a deux droites données A, E. Il faut, entre elles, intercaler deux droites moyennes proportionnelles, disons B, C. Autrement dit on doit avoir A : B :: B : C :: C : E...
Nous proposons de présenter la précision et la généralisation faites par Du Bois-Reymond et par Lebesgue de la condition d’intégrabilité R2.
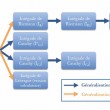
Nous affirmons que la technique utilisée notamment par Cauchy pour généraliser l’intégrale de Cauchy pour les fonctions continues (IC1) aux intégrales impropres (I*C1 ou IC2) s’apparente à une technique qui permet d’effectuer un transfert d’un apprentissage. En effet, Jacques Tardif propose la définition minimale suivante d’un transfert d’un apprentissage :
Nous retrouvons au 19e siècle quatre façons de définir ou de comprendre la notion mathématique d’intégrale : l’intégrale de Cauchy, l’intégrale de Riemann et les versions calculatoire et axiomatique de l’intégrale de Lebesgue. Nous proposons d’étudier les généralisations de ces façons de définir l’intégrale en introduisant deux types de généralisations : les généralisations conservatives et les généralisations innovantes. Dans le premier cas, la façon de définir l’intégrale ou de calculer l’intégrale est conservée et son extension est augmentée, c’est-à-dire qu’il y a plus de fonctions qui sont intégrables selon cette façon. Dans ce second cas, la façon de comprendre l’intégrale change et il y a une réinterprétation, voire une reconstruction de la notion.