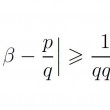CultureMath
De grands défis mathématiques d’Euclide à Condorcet n’est pas une histoire des grands problèmes mathématiques ou historiques. Cet ouvrage, la dernière production de la commission inter-IREM « épistémologie et histoire des mathématiques », ne restreint pas non plus l’histoire des mathématiques à ses seuls apports culturels qui, par ailleurs, ne sont pas négligés...
C’est l’heure de la célébration festive d’un anniversaire joyeux, d’un jubilé particulièrement important pour tous ceux qui aiment et qui enseignent les mathématiques : le centenaire de l’APMEP ! Ce faisant, nous célébrerons une fête des mathématiques qui, siècle après siècle, accumulent les occasions de vivre les beautés et les surprises de l’intelligence. En remontant dans le temps nous évoquerons ainsi les visions de Cantor, les constructions de Boliay, les machines de d’Alembert, et les aventures de Neper. Et nous évoquerons bien d’autres situations, concepts ou problèmes, qui ont fait, et qui font toujours, du jeu des calques mathématiques (ceux du formalisme, des représentations et des objets réels) le plus jubilatoire des jeux de l’esprit et de la connaissance.
La fonction zêta de Riemann, définie par $\displaystyle{\zeta ( s) = \sum_{ n=1}^{ + \infty} \frac{ 1}{ n^s}}$ (pour ${Re}~ s > 1$), intéresse les mathématiciens depuis longtemps, et elle est encore à l'heure actuelle très étudiée, car cette fonction est fortement liée aux propriétés des nombres premiers. Dans ce texte issu d'un Mémoire de M1, nous étudions quelques propriétés arithmétiques et algébriques des valeurs de $\zeta (s)$ aux points entiers $s \in \mathbb{N}$, $s \geqslant 2$, telles que l'irrationalité ou la transcendance. Notamment, nous fournissons une démonstration complète et élémentaire, due à Beukers, du théorème d'Apéry (1978) selon lequel $\zeta(3)$ est irrationnel; cette démonstration est tout à fait accessible à un étudiant de Licence ou de classes préparatoires.
Encart de l'article : $\sum_{n \geqslant 1}\, \frac{1}{n^3}$ est irrationnel.
Encart de l'article : $\sum_{n \geqslant 1}\, \frac{1}{n^3}$ est irrationnel.
On attribue au physicien Ernest Rutherford (1871-1937) la citation « All science is either physics or stamp collecting ». Malgré son caractère provocateur et caricatural, cette citation résume assez bien l’architectonique des sciences jusqu’à la fin du XXe siècle : la physique règne, une grande partie des mathématiques est motivée par ses applications à la physique, la biologie décrit et classe les espèces, les humanités ne sont pas encore les sciences humaines et la technique n’est qu’une application de la science.
Cet ouvrage a pour but d'amener le lecteur à la rencontre de textes scientifiques originaux, s'échelonnant pour la plupart du XVIIe au début du XXe siècle. Quinze scientifiques contemporains ont chacun choisi un texte ancien qu'ils aiment, manuscrit, article ou quelques pages d'un livre et en présentent une analyse. En suivant le texte de près, avec des citations abondantes, ils s'attachent à expliquer la démarche et la nature des résultats d'un savant dont la pensée compte encore à notre époque.
Au milieu du XIX° siècle, la percée de George Boole (1815-1864) pour 'algébriser' la logique est la concrétisation d'une lente évolution concernant, outre la logique elle-même, les mathématiques et leur rôle dans l'évolution des sciences. Si, dans sa forme brute, le calcul de Boole a pu déconcerter, ce n'est pas seulement par ses insuffisances avérées mais aussi par son existence même.
Ils sont présentés en français par Leonhard Euler (1707 – 1783) dans ses « Lettres à une princesse d'Allemagne » de la manière suivante...
Les propositions sont constituées d'un sujet, auquel une copule attribue un prédicat. Grammaticalement, la forme est nom + verbe + nom. Elles sont l'objet d'une double classification...