|
SOMMAIRE 1 . Introduction 2. Un contexte philosophique et scientifique: la question des fondements 2.1 Contexte philosophique : la crise de la causalité 2.2 Un contexte scientifique 2.2.1 La nature de la force de gravitation newtonienne 2.2.2 La mesure de la force d'un corps en mouvement ou la querelle dite des forces vives 2.2.3 Le statut des principes de la mécanique 3. Le contenu du Traité de la dynamique 3.1 Premier principe 3.2 Second principe 3.3 Troisième principe 3.4 Le principe de D'Alembert 3.5 Quelques exemples d'application 3.5.1 L'étude du mouvement du centre de gravité sans l'usage des forces 3.5.2 L'étude du centre d'oscillation sans l'usage du principe des forces vives 3.5.3 La démonstration du principe des forces vives 4. La postérité du Traité de dynamique Conclusion Encarts
Encart 2: Enoncé du "principe général" Encart 3 : Illustration de l'application du "principe de la dynamique" au cas du choc de corps durs |
1743
: premier coup et coup de maître. Alors tout juste
âgé de 26 ans et fraîchement
élu adjoint mécanicien à
l'Académie Royale des Sciences, Jean Le Rond D'Alembert
publie son premier et plus fameux ouvrage scientifique, le Traité de dynamique
(seconde éd. en 1758). Une ambition forte préside
au projet de cette rédaction, à savoir la
volonté, exprimée par son auteur, d' "aplanir
l'abord de la mécanique", afin d'en faire une "Science
claire" en démontrant ses "principes "
à partir "de la considération seule du mouvement"
; une économie de moyens -l'usage des seules
définitions du mouvement et des corps- devrait permettre
d'élever une science sur des bases pérennes. En
somme, D'Alembert estime les fondements de la mécanique
sujets à caution et sacrifie sur l'autel de la
clarté les principes et concepts qu'il juge incertains voire
sujets à erreur.
Mais d’où lui vient son scepticisme envers les fondements de la mécanique ? Sur quelles bases fonde-t-il lui-même sa science ? Coup de maître ou coup d'épée dans l'eau : son projet est-il exempt de reproches ? Quelle en est la postérité ? Autant de question qui guideront la rédaction du présent article.
Mais d’où lui vient son scepticisme envers les fondements de la mécanique ? Sur quelles bases fonde-t-il lui-même sa science ? Coup de maître ou coup d'épée dans l'eau : son projet est-il exempt de reproches ? Quelle en est la postérité ? Autant de question qui guideront la rédaction du présent article.
Un contexte philosophique et scientifique : la question des fondements
Contexte philosophique : la crise de la causalité
Aux
tournants des 17ème
et 18ème
siècles,
la mécanique semble se trouver dans une situation paradoxale
: tandis que la dynamique se développe, qu'Isaac Newton
(1642-1727) fait du concept de force la clef de voûte de son
œuvre phare promise à une immense
postérité, les Principes
mathématiques
de la philosophie naturelle (1687), apparaît
aussi dans les
années 1660 un courant de pensée anti-dynamiste.
Une doctrine philosophique d'inspiration cartésienne,
l'occasionnalisme auquel le philosophe Nicolas Malebranche (1638-1715)
donnera ses lettres de noblesse, développe en effet une
analyse critique de la causalité –comment
comprendre les actions réciproques entre l'âme et
le corps ou celles entre les corps ?- et ne voit en Dieu que l'unique
cause efficiente : les corps n'agissent pas en propre, le choc
n'étant qu'une occasion qui détermine l'exercice
de l'action divine. Il n'existe donc pas de forces dans la nature et
ces réflexions entraînent un vaste mouvement de
scepticisme quant à la possibilité de
développer une mécanique autrement que comme une
science des effets : ce recours à Dieu ne se veut pas une
solution de facilité, mais la reconnaissance de
l'impossibilité de comprendre la nature de la cause,
impossibilité impliquant de ne s'en tenir qu'aux
phénomènes.
Quelle connaissance avait D'Alembert de ce genre de réflexions ? Alors encore élève au collège des Quatre Nations (ou collège Mazarin), il recevra l'enseignement du professeur Adrien Geffroy, malebranchiste convaincu ; il n'ignore donc pas l'occasionalisme. Dans l'édition de 1743 du Traité de dynamique, il cite un ouvrage de Trabaud (Principes sur le mouvement et l’équilibre, pour servir d’introduction aux Mécaniques & à la Physique, 1741) qui se réfère de nombreuses fois aux thèses de Malebranche, ce qu'un lecteur attentif ne peut manquer. D'Alembert développe aussi ce qu'on nomme "l'argument de l'inconcevable", qui figure originellement chez Pierre-Louis Moreau de Maupertuis (Discours sur les différentes figures des astres, où l’on essaye d’expliquer les principaux phénomènes du Ciel, 1732), à savoir que l'explication de la gravité basée sur une impulsion (thèse de type cartésienne) n'est pas plus intelligible que l'attraction newtonienne, la force dans chacune de ces hypothèses demeurant incompréhensible, comme l'enseignent les réflexions occasionalistes. Enfin, dans l'article Mouvement de l'Encyclopédie, D'Alembert se réfère à un livre du philosophe suisse Jean-Pierre de Crousaz (Essay sur le mouvement, 1728) dans lequel se trouve inséré un mémoire qui remporta le prix de l'Académie Royale des Sciences de 1720, pièce s'inspirant en partie de Malebranche.
Quelles influences ces analyses critiques de la causalité exercèrent sur D'Alembert ? Bien que les certitudes manquent, notons que dans son projet d'épurer la mécanique de notions ambiguës, D'Alembert a une cible de choix : les forces, qualifiées dans son Traité "d'êtres obscurs & métaphysiques". Il écrit alors envisager "plutôt la Mécanique comme la Science des effets, que comme celle des causes" et avoir "détourné la vue de dessus les causes motrices" pour ne considérer que le mouvement qu'elles produisent. Autant de propos permettant d'inscrire son travail dans le prolongement des réflexions sur la causalité précédemment mentionnées.
Quelle connaissance avait D'Alembert de ce genre de réflexions ? Alors encore élève au collège des Quatre Nations (ou collège Mazarin), il recevra l'enseignement du professeur Adrien Geffroy, malebranchiste convaincu ; il n'ignore donc pas l'occasionalisme. Dans l'édition de 1743 du Traité de dynamique, il cite un ouvrage de Trabaud (Principes sur le mouvement et l’équilibre, pour servir d’introduction aux Mécaniques & à la Physique, 1741) qui se réfère de nombreuses fois aux thèses de Malebranche, ce qu'un lecteur attentif ne peut manquer. D'Alembert développe aussi ce qu'on nomme "l'argument de l'inconcevable", qui figure originellement chez Pierre-Louis Moreau de Maupertuis (Discours sur les différentes figures des astres, où l’on essaye d’expliquer les principaux phénomènes du Ciel, 1732), à savoir que l'explication de la gravité basée sur une impulsion (thèse de type cartésienne) n'est pas plus intelligible que l'attraction newtonienne, la force dans chacune de ces hypothèses demeurant incompréhensible, comme l'enseignent les réflexions occasionalistes. Enfin, dans l'article Mouvement de l'Encyclopédie, D'Alembert se réfère à un livre du philosophe suisse Jean-Pierre de Crousaz (Essay sur le mouvement, 1728) dans lequel se trouve inséré un mémoire qui remporta le prix de l'Académie Royale des Sciences de 1720, pièce s'inspirant en partie de Malebranche.
Quelles influences ces analyses critiques de la causalité exercèrent sur D'Alembert ? Bien que les certitudes manquent, notons que dans son projet d'épurer la mécanique de notions ambiguës, D'Alembert a une cible de choix : les forces, qualifiées dans son Traité "d'êtres obscurs & métaphysiques". Il écrit alors envisager "plutôt la Mécanique comme la Science des effets, que comme celle des causes" et avoir "détourné la vue de dessus les causes motrices" pour ne considérer que le mouvement qu'elles produisent. Autant de propos permettant d'inscrire son travail dans le prolongement des réflexions sur la causalité précédemment mentionnées.
|
Figure 1
 Le philosophe Nicolas
Malbranche (1638-1715)
|
Un contexte scientifique
Le temps des querelles
Mais il n'existe pas qu'un contexte philosophique venant jeter le trouble sur une physique de type causale. Trois grands débats impliquent la force et son statut ; D'Alembert en héritera, voire y prendra part.
La nature de la force de gravitation newtonienne
Si,
dans ses Principes,
Newton écrit qu'il ne faut voir derrière la force
d'attraction rien d'autre qu'une grandeur mathématique, il
n'en demeure pas moins que des savants influencés
par les
théories de Descartes -essentiellement des
français- considèrent qu'il s'agit là
d'un retour aux "qualités occultes", aux
êtres obscurs dont on douait les corps et qui abondaient
durant la période de la Renaissance. Aussi estiment-ils que
seuls les contacts entre les corps –les planètes
sont transportées par un fluide- permettent un mouvement
alors
qu'a contrario
une action à distance demeure inconcevable. Etre obscur pour
les uns, simple vérité de faits pour les autres
ou bien encore propriété de la matière
selon certains newtoniens, le débat engagé autour
de cette force a sa part d'idéologie mais aussi de
chauvinisme, le secrétaire perpétuel de
l'Académie Royale, B. Le Bovier de Fontenelle
n'hésitant pas, dans son Eloge de Newton de
1727, avec un parti pris évident, à mettre sur un
pied d'égalité Descartes et Newton. Sans doute
inspiré par Maupertuis, D'Alembert écrit dans son
Traité
que la gravitation fait partie des "causes qui se font
connaître par leur effet, & nous en ignorons
entièrement la nature" ; ainsi, la loi de chute des corps
est donnée par "l'expérience", "sans
connaître la cause de la pesanteur". Aussi D'Alembert
prône-t-il de ne s'en tenir qu'aux seuls effets
mesurés.
La mesure de la force d'un corps en mouvement ou la querelle dite des forces vives
Pour
les partisans de G. W. Leibniz, la force d'un corps de masse m et de
vitesse v s'estime par mv²
; pour la plupart des français
(dont J.-J. Dortous de Mairan, Dissertation
sur l'estimation et sur la mesure des forces motrices des corps,
1728) et anglais (dont le disciple écossais de Newton, C.
MacLaurin, Dissertation
des lois du choc des corps, 1724) par mv. La
polémique commence en 1686, année où
Leibniz publie un mémoire critique à l'encontre
de Descartes (Brevis
demonstratio), lequel commettrait l'erreur de mesurer la
force d'un corps par sa quantité de mouvement, et
s'étend jusque dans les années 1740. Selon
Leibniz, la force se mesure par la hauteur du poids qu'elle permet
d'élever. Or, s'appuyant sur la loi de Galilée de
chute libre des corps -l'espace parcouru est comme le carré
du temps de chute, et la vitesse comme ce temps- la mesure mv²
s'ensuit. Des expériences comme celles menées par
le hollandais s'Gravesande (Remarques
sur la force des corps en mouvement et sur le choc, 1728),
et des écrits plus théoriques (Jean Bernoulli,
Discours sur les lois de la communication du mouvement, 1724 et 1726)
confortent cette thèse. Du point de vue strictement
scientifique –car Leibniz développe toute une
métaphysique, la force vive exprimant l'essence dynamique de
la matière, les cartésiens définissant
pour leur part cette dernière par son étendue
géométrique -, le débat tient au choix
de la variable à prendre en compte dans la mesure de
l'effet. Les leibniziens considèrent l'espace parcouru comme
essentiel et leur "force" s'estime par
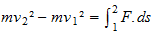
avec ds un élément d'espace parcouru par un corps de masse m sous l'action d'une force (au sens actuel) F, et v1 et v2 les vitesses aux positions 1 et 2 du corps ;cette égalité correspond au théorème de l'énergie cinétique, Leibniz nommant mv² la force vive. Pour ceux faisant intervenir le temps, il vient
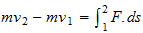
où on reconnaît l'expression d'une impulsion obtenue à partir du théorème fondamental de la dynamique (F = ma, F la force produisant sur la masse m une accélération a).
D'Alembert qualifie la querelle de "dispute de mots", la jugeant "inutile" et estimant y mettre un terme. Il dépasse la question de la véritable mesure, question venant conférer une réalité à la force, en estimant qu'au fond les deux proposées peuvent bien coexister. En effet, le terme force ne signifie rien d'autre à ses yeux que la "propriété" des corps à surmonter des obstacles, ou l'effet produit en les surmontant. La diversité d'effets entraîne donc celle de la mesure et D'Alembert juge qu'il n'y a pas là d'"inconvénient". Ainsi, si le corps est en équilibre, il faudra retenir mv, tandis que mv² correspondra au cas d'un mouvement décéléré (ascension d'un poids). Fidèle à sa critique de la force, D'Alembert entend donc se placer au-dessus de la mêlée : l'éviction du concept entraîne par le même coup celle d'un faux problème, à savoir la recherche de sa vraie mesure.
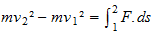
avec ds un élément d'espace parcouru par un corps de masse m sous l'action d'une force (au sens actuel) F, et v1 et v2 les vitesses aux positions 1 et 2 du corps ;cette égalité correspond au théorème de l'énergie cinétique, Leibniz nommant mv² la force vive. Pour ceux faisant intervenir le temps, il vient
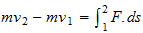
où on reconnaît l'expression d'une impulsion obtenue à partir du théorème fondamental de la dynamique (F = ma, F la force produisant sur la masse m une accélération a).
D'Alembert qualifie la querelle de "dispute de mots", la jugeant "inutile" et estimant y mettre un terme. Il dépasse la question de la véritable mesure, question venant conférer une réalité à la force, en estimant qu'au fond les deux proposées peuvent bien coexister. En effet, le terme force ne signifie rien d'autre à ses yeux que la "propriété" des corps à surmonter des obstacles, ou l'effet produit en les surmontant. La diversité d'effets entraîne donc celle de la mesure et D'Alembert juge qu'il n'y a pas là d'"inconvénient". Ainsi, si le corps est en équilibre, il faudra retenir mv, tandis que mv² correspondra au cas d'un mouvement décéléré (ascension d'un poids). Fidèle à sa critique de la force, D'Alembert entend donc se placer au-dessus de la mêlée : l'éviction du concept entraîne par le même coup celle d'un faux problème, à savoir la recherche de sa vraie mesure.
Le statut des principes de la mécanique
En 1756, l'académie de Berlin, sous l'initiative
du savant Leonard Euler, propose d'examiner "si les lois de la statique
et de la mécanique sont de vérité
nécessaire ou contingente". On trouve trace de telles
réflexions dès la première
moitié du 18ème siècle, chez des
auteurs comme Pierre Varignon, figure majeure des sciences
physico-mathématiques françaises de cette
période, ou sous la plume de Fontenelle. D'Alembert estime
nécessaire les principes sur lesquels il fonde sa
mécanique : pour lui, cela signifie que leur
découverte à partir des seules
définitions de la matière et du mouvement doit
coïncider avec ce que l'expérience enseigne. A contrario, si
cette dernière infirme le raisonnement, elle seule permet de
fonder une science dont les principes ne sont alors que des
vérités contingentes. Concernant le concept de
force, le principe fondamental de la dynamique (F = ma) est
érigé par Euler comme une
vérité nécessaire : il s'agit d'un
théorème démontré
à partir de la nature de la force et de son action (Mechanica sive motus scientia
analytice exposita, 1736). D. Bernoulli voit dans ce
principe une vérité empirique donc contingente (Examen principiorum mechanicae
et demonstrationes geometricae de compositione et resolutione virium,
1726). D'Alembert rejette chacune des deux thèses pour ne
faire de la formule qu'une simple définition (voir Encart 1) : Euler
voit la mariée trop belle, la nature du concept de force
demeurant incompréhensible, comment fonder en
nécessité une telle formule ? La position de
Bernoulli ne consiste à faire de la mécanique
qu'une science expérimentale, D'Alembert la concevant comme
une branche des mathématiques. Il refuse alors les termes
d'un débat qui impliquerait un examen du statut de la force
puisque, de par son caractère "obscur", elle ne saurait
fonder des principes nécessaires servant à
l'édifice d'une science "claire".
Chacun de ces débats entraîne une prise de position de D'Alembert relative à la force. L'obscurité de sa nature comme le doute porté sur sa mesure contribuent sans doute à la naissance d'une attitude sceptique conduisant à souligner l'inanité de la recherche des causes et la nécessité de ne s'en tenir qu'aux seuls effets mathématisés ; position qui sera une constante dans toute son œuvre.
Chacun de ces débats entraîne une prise de position de D'Alembert relative à la force. L'obscurité de sa nature comme le doute porté sur sa mesure contribuent sans doute à la naissance d'une attitude sceptique conduisant à souligner l'inanité de la recherche des causes et la nécessité de ne s'en tenir qu'aux seuls effets mathématisés ; position qui sera une constante dans toute son œuvre.
|
Figure 2
 Pierre Varignon (1654 - 1722) |
Le contenu du Traité de dynamique
La lecture des Opuscules mathématiques de D'Alembert apparaît bien complexe, tant par le contenu que par le caractère parfois décousu de la rédaction, l'auteur donnant l'impression d'écrire au fil de l'inspiration, avec ce caractère brouillon inhérent à la recherche. Le Traité de dynamique est d'une toute autre nature : certes, la complexité est bien là, mais la rédaction est cohérente avec un ordre de progression allant des principes premiers –des éléments de mécaniques- à l'énoncé d'un principe fondamental et son application.
Le livre s'ouvre par un "Discours préliminaire" – "Préface" dans l'édition de 1743 -, contient quelques "Définitions et Notions préliminaires"(incluant la définition du "Corps"comme "étendue impénétrable"), puis se compose de deux parties. La première s'intitule "Lois générales du mouvement & de l'équilibre des Corps" et contient la démonstrations des "principes" sur lesquels D'Alembert entend fonder une "science claire". La seconde, "Principe général pour trouver le Mouvement de plusieurs Corps qui agissent les uns sur les autres d'une manière quelconque ; avec plusieurs applications de ce Principe", comprend l'énoncé du principe dit de D'Alembert (une telle appellation semble postérieure au 18ème siècle) et son application à 14 problèmes.
Dans son Discours préliminaire, D'Alembert énonce son projet de ce livre ayant pour "double objet" de "reculer les limites de la Mécanique, & [...] en aplanir l'abord". A cette fin, il énonce que sa mécanique repose sur trois principes, "celui de l'équilibre joint à ceux de la force d'inertie & du mouvement composé", démontrés "par la seule considérations du Mouvement, envisagé de la manière la plus simple & la plus claire", à savoir "le transport du mobile d'un lieu dans un autre". Cette dernière définition à sa part de polémique : D'Alembert récuse le recours à "des forces inhérentes au Corps en Mouvement" permettant de justifier sa continuation et ne conçoit le mouvement que dans son aspect géométrique. Trois principes démontrés, épurés des chimères métaphysiques que sont les forces, devraient constituer un socle suffisamment solide sur lequel élever toute la mécanique.
|
Figure 3
 |
Pour leurs démonstrations, D'Alembert recourt à un principe supra-géométrique, le principe de raison. La combinaison des trois principes donne naissance au "principe général" ou à une "méthode générale" permettant la résolution des "plus difficiles problèmes" relatifs aux chocs ou à la traction de corps par le bais de fils ou verges inflexibles, soit des problèmes du ressort de ce que D'Alembert nomme la "dynamique". La définition du terme permet d'éclairer ce paradoxe, à savoir, l'appellation de Traité de dynamique pour un ouvrage récusant l'usage des forces. Déjà, en 1736, Alexis-Claude Clairaut, académicien des sciences, publie un mémoire intitulé De quelques Problèmes de Dynamique dans lequel il conçoit cette science comme "une Classe de Problèmes Physico-mathématique" ayant pour but l'étude du mouvement des corps soumis à des forces initiales et "liés ensemble par des fils" tels "qu'ils s'altèrent réciproquement leur mouvement". Clairaut écrit que cette recherche sur les systèmes à liaison lui vient de la question des "tractoires", courbes décrites sur un plan horizontal lorsque l'extrémité d'un fil suit une droite donnée tandis que l'autre est chargée d'un poids : la droite devient courbe quelconque et "insensiblement cela […] conduit à une plus grande recherche, pour peu qu'on pense à ce genre de Problème, il en vient dans l'esprit beaucoup d'autre de la même nature". Les variantes à ce genre de problèmes sont généralement résolues par Clairaut à l'aide du "principe des forces accélératrices" (le F = ma) et du principe des forces vives, qu'il s'agisse de ce mémoire de 1736 ou de celui de 1742, Sur quelques principes qui donnent la Solution d'un grand nombre de Problèmes de Dynamiques ; ceci revient à l'utilisation du théorème de l'énergie cinétique. Aussi, si les deux savants se rejoignent sur les thèmes, ils se séparent sur les méthodes, en ajoutant que Clairaut énonce des "principes" sans cependant livrer une réflexion philosophique comme le fait D'Alembert. Et une telle réflexion détermine la démonstration de ses trois principes fondamentaux.
Premier principe
Le chapitre I de son livre s'intitule "De la force d'inertie, & des propriétés du mouvement qui en résultent". Pour cette appellation, D'Alembert renvoie à Newton et à ses Principes (loi I) : il s'agit de la "propriété qu'ont les Corps de rester en l'état où ils sont". D'Alembert démontre deux "lois": la première relative à la conservation du repos, la seconde, à celle de la direction du mouvement. La clef de voûte du raisonnement tient à l'emploi du principe de raison : D'Alembert invoque que sans "causes étrangères", "il n'y a pas de raison" pour que le repos donne lieu à un mouvement -en déduit plus généralement qu'une vitesse ne peux pas changer spontanément-, ou encore qu'"il n'y a pas de raison" pour qu'un mobile change de direction. Sur ce dernier point, D'Alembert démontre sa proposition en se plaçant sous deux hypothèses : d'une part, en supposant que la "cause motrice" n'agisse qu'instantanément –un choc de corps durs- et, d'autre part, qu'elle agisse continuellement afin d'assurer la persistance du mouvement. Il n'entend pas adhérer à cette dernière hypothèse car, tout au contraire, il récuse toute démonstration se basant sur des forces inhérentes aux corps : il s'agit en somme d'un cas d'école, et la démonstration sous chaque hypothèse vise à justifier la généralité de la loi.
Il poursuit en donnant une définition du mouvement uniforme puis une "Remarque" concernant "la mesure du tems" que seul ce mouvement permet. Par degrés croissants de complexité, il en vient alors au "mouvement accéléré ou retardé" ; comment l'aborde-t-il étant entendu qu'une accélération suppose une force, concept qu'il entend proscrire de ce livre ? Pour D'Alembert, c'est le mouvement qui définit la force et non la force, comme une entité première qui existerait dans la nature, qui provoque le mouvement (voir Encart 1). La démarche illustre ainsi parfaitement les positions épistémologiques figurant dans le Discours préliminaire, D'Alembert développant une théorie de la définition remettant à plat, par la considération des seuls effets mesurés (une accélération), les fondements de la dynamique qui lui paraissent obscurs.
Second principe
Il apparaît dans le chapitre II, "Du mouvement composé", qui se compose d'un unique théorème, celui du parallélogramme des forces : si un corps A est soumis à deux "puissances" (forces) lui faisant parcourir uniformément AB et AC pendant le même temps, il parcourra uniformément la diagonale AD du parallélogramme construit sur AB et AC sous l'action simultanée de ces deux "puissances" durant ce temps. La démonstration de D'Alembert repose sur la mobilité d’un plan (KLMH) par rapport à l’ "espace absolu". Un corps A situé sur ce plan et soumis aux deux "puissances" agissant continuellement ou instantanément décrit d’un mouvement rectiligne uniforme une ligne Ag ; il faut justifier que cette dernière et la diagonale AD de ABDC se confondent. D’Alembert imagine que le plan KLMH franchisse AB et AC pendant la durée T avec les mêmes mouvements uniformes que produisent les deux "puissances", mais selon des sens opposés à chacune d’elles. Ainsi, "le point mobile A, est tiré continuellement en cet état par quatre puissances contraires & égales deux à deux, & [...] par conséquent, il doit rester en repos dans l’espace absolu".
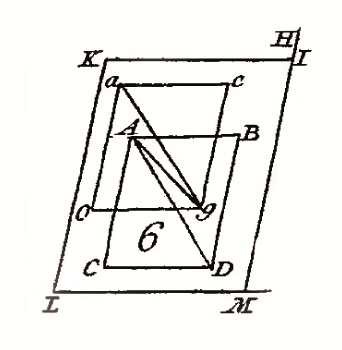 |
Par ce mouvement de KLMH, le
point g du plan décrit une ligne ga égale et
parallèle à AD, diagonale de ABCD. Or, pour que
le corps A demeure immobile dans l’espace absolu, il faudra
que a et A coïncident à l’issue de la
combinaison du mouvement produit par les « puissances
» (Ag) avec celui du plan.
L’égalité et le parallélisme
de AD et ag, la coïncidence de A et a, conduisent à
identifier Ag et AD.
|
D'Alembert récuse une démonstration reposant sur l'artifice d'une règle mobile -A se déplaçant uniformément sur la règle AB pendant que AB glisse uniformément le long de AC ; ce raisonnement figure dans le livre de Varignon de 1725-, car il restreint la généralité du propos : D'Alembert suppose une action continuelle ou instantanée, la règle impliquant une action permanente. Il refuse aussi une analyse fondée sur un "axiome" qui prétendrait que "l'action de causes conjointes est égal à la somme de leurs effets pris séparément", et qui viendrait introduire une proportionnalité de l'effet à sa cause et ferait ainsi tomber dans les obscurités inhérentes aux analyses se basant sur les forces. D'Alembert fait donc seulement usage de "l'espace parcouru & du tems employé à la parcourir". Sa démonstration s'appuie cependant aussi sur les acquis de la loi II précédente : il se place en effet sous cette double hypothèse d'une action instantanée ou de la persistance d'une cause motrice (action continuelle) pour justifier la permanence d'un mouvement rectiligne uniforme. Ainsi, ce théorème, tout comme la loi II, repose sur le principe de raison.
Troisième principe
Ce dernier apparaît dans le Chapitre III, "Du Mouvement détruit ou changé par des obstacles". D'Alembert le nomme "principe de l'équilibre" et il se présente comme celui du "mouvement composé", à savoir sous la forme d'un "théorème" démontré à l'aide du principe de raison. D'Alembert énonce que si deux corps de même quantité de mouvement ont des directions opposées de telle sorte qu'ils ne puissent se déplacer mutuellement, il y aura équilibre. Pour des masses et vitesses égales, il juge "évident" le repos qui s'ensuit, ne voyant dans ce cas "point de raison" pour qu'un corps se meuve plutôt que l'autre comme le suggère la symétrie du problème. Il démontre ensuite que l'équilibre survient pour les cas plus généraux où les masses et vitesses des corps sont inégales mais inversement proportionnées de telles sorte que els quantités de mouvement respectives soient égales. Cette interprétation du choc de corps durs de même quantité de mouvement en terme d'équilibre s'avère classique. Elle apparaît, entre autre, chez Antoine Parent, académicien des sciences, qui en fera usage dans sa détermination des règles du choc, voir Essais et recherches de mathématique et de physique, 1713). Sa méthode, impliquant une décomposition de mouvement et un équilibre de quantités de mouvement égales, n'est pas sans rapport avec celle développée par D'Alembert, même s'il demeure difficile de savoir dans quelle mesure ce dernier s'inspire de ses aînés.
La combinaison de chacun de ses principes démontrés à l'aide du principe de raison va donner naissance au "Principe général" exposé dès le début de la seconde partie du livre.
Le principe de D'Alembert
Cette seconde partie se compose de quatre chapitres, le premier exposant le "principe général", dont l'application permet de trouver des propriétés du centre de gravité d'un système de corps –second chapitre-, la résolution de problèmes de dynamique (au nombre de 14) –troisième chapitre constituant environ les deux tiers du livre- et la démonstration "Du principe de la conservation des forces vives"(intitulé du chapitre IV).
Le "principe général" se présente sous la forme d'un "problème général" (voir Encart 2 pour son énoncé) dans lequel D'Alembert cherche les mouvements pris par chacun des corps d'un système auxquels on impose des mouvements initiaux qu'ils ne peuvent suivrent en raison de leurs actions mutuelles. Il s'agit donc d'étudier des cas de collisions ou le mouvement de systèmes à liaisons inflexibles (verges, fils) comme, par exemple, le mouvement de pendules composés (voir infra) ou bien encore celui de deux corps sur un plan horizontal, l'un coulissant le long d'un fil au bout duquel l'autre est attaché, l'extrémité libre du fil étant reliée fixement au plan, les deux corps se voyant soumis à des mouvements initiaux quelconques (Problème 8). Ce type de problèmes correspond à ceux rencontrés dans le mémoire de Clairaut. Par quelle méthode D'Alembert entend les résoudre ?
La combinaison de la décomposition particulière mentionnée dans le cas du choc oblique et du principe de l'équilibre est la pierre angulaire de la méthode. D'Alembert imagine les corps A, B, C etc. soumis aux mouvements a, b, c etc. qu'ils changent à cause de leurs actions mutuelles en a, b, c, etc. Il considère alors a, b, c etc. comme composés de a, b, c etc. et d'autres α, β, χ etc. Puisque les corps prennent les mouvements finaux a, b, c etc. il suit que le système soumis au seuls α, β, χ etc. reste au repos ou, dit autrement, ces mouvements se détruisent mutuellement ou encore eux seuls imposés aux corps entraînent l'équilibre du système. Ainsi la méthode repose sur une décomposition en composantes qui ne se nuisent pas (a, b, c etc. les mouvements finaux que les corps suivent librement, c'est-à-dire sans interagir mutuellement) et en mouvements détruits par les interactions mutuelles (voir Encart 3 pour une application du principe au cas du choc des corps durs). Les mouvements équilibrés donnent lieu à une équation qui permettra l'étude du mouvement du système (voir infra l'exemple du pendule).
D'Alembert fonde ainsi l'interaction mécanique sur des mouvements fictifs détruits, c'est-à-dire équilibrés ; l'équilibre devient sous-jacent à l'ensemble des événements dynamiques. Il ne s'agit plus d'étudier l'interaction par le biais d'une force agissant extérieurement sur un système, ce qui correspond à une mécanique de type newtonienne, mais par les mouvements empêchés de ce système lui-même. Le principe illustre alors le parti pris de son auteur de fonder la mécanique sans le recours à un concept de force. Concernant son origine, l'historien en est réduit aux spéculations. Il semble que la question des collisions de corps (choc oblique et règles du choc) soit importante. D'Alembert développe un passage sur les collisions oblique et directe sur des surfaces fixes (chapitre III : "Du Mouvement détruit ou changé par des obstacles"). L'intérêt de ces collisions tient davantage à la méthode pratiquée –une décomposition originale du mouvement initial qui est au cœur de son "principe général"-qu'à la solution du problème – la détermination de la vitesse du corps après le choc. Pour le choc oblique, D'Alembert suppose la vitesse initiale composée de la vitesse finale (celle du corps roulant sur le plan après la collision) et d'une détruite, la composante perpendiculaire au plan. Ainsi, il renverse une perspective dynamique qui invite à analyser un choc par le biais d'une force agissant sur un mouvement initial : pour D'Alembert, ce dernier renferme une composante dont "l'anéantissement", la "destruction", donne la solution du problème – la vitesse résiduelle étant l'autre composante inchangée. S'ensuit une étude du mouvement d'un corps sur des surfaces courbes assimilées à des polygones de côtés infiniment petits requerrant les acquis de la collision oblique précédente et des considérations infinitésimales. La séquence associant collision oblique et mouvement sur des courbes ainsi que la méthode employée se retrouvent chez des auteurs comme Varignon (1693, 1704, 1725) et Trabaud (1741) ; D'Alembert s'inscrit-là dans des pratiques courantes, ce qui n'est sans doute pas sans importance pour comprendre l'origine de son fameux "principe général" qui repose sur cette décomposition originale d'un mouvement initial. L'autre hypothèse la plus probante concerne la question du centre d'oscillation (voir infra).
Quelques exemples d'application
L'étude du mouvement du centre de gravité sans l'usage des forces
Le "théorème I" du chapitre II ("Propriétés du centre de gravité commun de plusieurs Corps, déduites du principe précédent") énonce que "l’état de Mouvement ou de repos du centre de gravité de plusieurs Corps, ne change point par l’action mutuelle de ces corps entr’eux, pourvû que le systême soit entierement libre, c’est-à-dire qu’il ne soit point assujetti à se mouvoir autour d’un point fixe". D’Alembert décompose les mouvements a, b, c etc., imprimés aux corps A, B, C etc. en a, b, c etc. et α, β, χ etc. Inversement, il considère que a, b, c peuvent se concevoir comme composés a, b, c etc. et - α,- β, - χ etc. Le mouvement du centre de gravité système, en supposant les corps animés de a, b, c etc., sera le même que si nous les supposions d’abord mus avec a, b, c, etc. et ensuite avec - α,- β, - χ etc. Par hypothèse, l'absence de point fixe entraîne - α,- β, - χ etc. = 0 ; les corps soumis aux seuls mouvements - α,- β, - χ etc. s’équilibrent et, ainsi, en ne tenant compte que d'eux seuls, "le chemin du centre de gravité est zéro". En application du "principe", les mouvements des corps finaux des corps sont a, b, c etc. et ainsi le chemin du centre de gravité est le même quand les corps ont ces mouvements ou a, b, c, etc. imprimés initialement.
Un tel théorème figure
dans les Principes de Newton mais
en
tant que corollaire (le troisième) de sa loi
d'égalité entre l'action et la
réaction, soit comme une conséquence d'une vision
dynamique de l'interaction.
Aussi, si classique que soit la proposition, D'Alembert entend lui
donner un
autre fondement, l'usage de sa "méthode
générale" requerrant des
"principes" évinçant le concept de force.
L'étude du centre d'oscillation sans l'usage du principe des forces vives
D'Alembert regroupe ces problèmes, tous figurant dans le chapitre III ("Problèmes où l'on montre l'usage du Principe précédent"), en quatre catégories : "Des corps qui se tiennent par des fils ou par des verges"; "Des corps qui vacillent sur des plans"; "Des corps qui agissent les uns sur les autres par des fils, le long desquels ils peuvent couler librement"; "Des corps qui se poussent ou qui se choquent", incluant les collisions de corps durs (indéformables) et élastiques. L'exemple qui suit fait partie de la première catégorie. Ce problème consiste à trouver la vitesse des corps A, B, R etc. attachés sur une verge CR fixe en C et oscillant autour de ce point. AO, BQ, RT correspondent aux "lignes infiniment petites" parcourues en un même temps par chacun des corps en supposant que la verge ne relie pas ; RT, BQ, AO aux vitesses imprimées initialement et décomposées en RS, ST ; BG, -GQ, AM, -MO, les premiers termes de chaque couple représentant la vitesse finale de chaque corps et, le second terme, la vitesse détruite par la verge. Des grandeurs telles que A.AM ou B.BG etc. expriment les "puissances"(forces) exercées sur chaque corps ; A.AM.AC, B.BG.BC etc. l'action de ces "puissances"sur les bras de levier CA et CB.
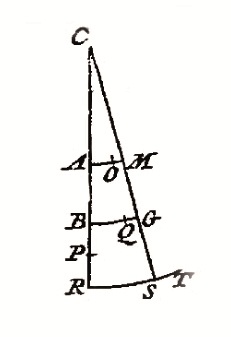 |
Il
suit, en application du "principe", que le système soumis
aux seules vitesses ST, - GQ, - MO demeure au repos ce qui correspond
à la mise en équation suivante, A.MO.AC + B.GQ.BC
= R.ST.CR, soit A.(AM-AO).AC+B.(BG-BQ)=R.(RT-RS).CR (1) ;
cette équation correspond à la
condition d'équilibre sur un levier, la somme des produits
de chaque "puissance" par sa distance au point d'appui C devant
être nulle. Or, AO (= a) et BQ (= b) sont données, et
puisque AM et BG peuvent s'exprimer en fonction de RS,
l'équation donnera l'expression de RS. En effet, en posant
RS = z, CA = r, CB = r' et CR = ρ il
vient 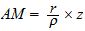 et 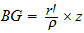 avec RT = c, il suit à l'aide de (1) et en isolant z 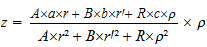 |
A l'aide de cette dernière formule, D'Alembert résout la question dite du centre d'oscillation : il s'agit de trouver la longueur x d'un pendule isochrone (même période d'oscillation) au pendule composé étudié. Dès 1673, C. Huygens donnait la solution de ce problème à l'aide du principe des forces vives (Horologium oscillatorium) ; il inaugure ainsi l'examen du mouvement de systèmes à liaisons –plus seulement celui d'un point matériel-, soit cette classe de problèmes que D'Alembert qualifie de dynamiques. Malgré tout, ce dernier ne peut se satisfaire de l'analyse de Huygens qui requiert l'usage d'un principe emprunt de métaphysique ; son analyse repose donc sur son propre principe. Ainsi, en nommant F, f, ϕ , les "forces motrices" agissant sur A, B, R, ayant respectivement pour expression Aa, Bb, Rc – D'Alembert nomme "forces motrices" les produits des masses par les accélérations ou vitesses infiniment petites acquises pendant un temps infiniment petit, et "forces accélératrices" ces seules vitesses – il obtient l'expression de la "force accélératrice" f1 de R sur la verge qui répond à une équation du type f1 × ds = u × du (voir Encart 1, u la vitesse de R, ds un élément d'espace parcouru) soit
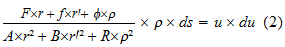
Quant au pendule simple de longueur x soumis à une force quelconque , il suivra aussi l'équation f2 × ds' = u' × du' (3) ; l'hypothèse d'une même période d'oscillation que le composé implique une expression de u' en fonction de u et x ; l'identification de (2) et (3) permet alors de déterminer x.
Ce problème du centre d'oscillation est traité en 1703 sur la base d'une méthode assez semblable par Jacques Bernoulli. D'Alembert fait référence à cette solution dans l'art. Oscillation de l'Encyclopédie ; elle constitue une possible hypothèse concernant l'origine de son principe.
Outre les 13 autres problèmes de cette partie, D'Alembert entend démontrer, dans le dernier chapitre, la conservation des forces vives à l'aide de son principe ; celui-là deviendra un principe dit "secondaire" (art. Dynamique, Encyclopédie), certes utile mais dérivé d'un plus général et strictement rationnel, cette rationalité balayant alors la portée métaphysique de la force vive.
La démonstration du principe des forces vives
Cette démonstration apparaît dans le chapitre IV de la seconde partie ("Du Principe de la conservation des forces vives"). Ce principe de conservation –il s'agit de celle de l'énergie cinétique d'un système- pose en effet problème à D'Alembert. D'une part, des savants l'érigent en principe fondamental bien que ses démonstrations soient insuffisantes–c'est le reproche adressé à D. Bernoulli. D'autres n'en font qu'une vérité empirique et, ainsi, la mécanique n'a pas un statut de vérité nécessaire. Puis, la force vive dépend de thèses métaphysiques, Leibniz en faisant l'expression mathématique d'une force inhérente à la matière. Enfin, ce principe manque d'universalité, puisque applicable aux seuls cas de collisions de corps élastiques ou pour des corps durs agissant continûment sans collision. Aussi cristallise-t-il à lui seul une multitude de défauts et de thèses à rejeter.
D'Alembert établit tout d'abord le principe de conservation pour un système composé de deux points matériels A et B reliés à une verge inflexible AB.
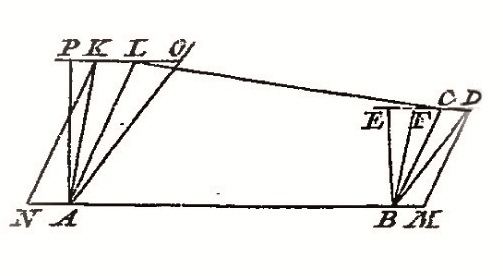 |
A et B
se voient imprimées des vitesses initiales
représentées par des lignes infiniment petites
AK, BD, vitesses modifiées en vertu de la liaison en AL et
BC. Il faut établir que A.AK² + B.BD² =
A.AL² + B.BC². D'Alembert construit les parallélogrammes ALKN et BCDM, puis décompose les vitesses initiales en vitesses résultantes et détruites, AK = AL + LK (AN) et BD = BC + CD (BM), ce qui, en élevant au carré et en multipliant par les masses A et B, donne A.AK² = A.AL² + 2 A.AL.LK+A.LK² (1) et B.BD² = B.BC² + 2B.BC.CD +B.CD² (2). L'hypothèse de l'inflexibilité de la verge (AB = LC) associée à l'application de son principe (A.AN + B.BM = 0 soit A.LK + B.CD = 0) laissent de l'addition de (1) avec (2) l'équation A.AK² + B.BD² = A.AL² + A.LK² + B.BC² + B.CD². |
En supposant AN (= LK) et BM (= CD) infiniment petites, soit dans le cas de vitesses initiales et finales différant infiniment peu l'une de l'autre, D'Alembert fait disparaître la somme A.LK² + B.CD². La conservation de la force vive se vérifiera alors sous cette dernière condition qui revient à supposer des changements de vitesses s'opérant d'une manière continue. La validité du principe se voit ensuite étendue aux systèmes de fils et verges composés de multiples points matériels puis de masses finies, aux collisions élastiques impliquant des corps de masses finies ou non, et au mouvement des fluides. Et le livre se clôt sur l'annonce de la publication prochaine (1744) du Traité de l'équilibre et du mouvement des fluides.
La postérité du Traité de dynamique
J.-L. Lagrange, correspondant et ami de D'Alembert, estime que le mérite de son aîné tient à cette innovation d'avoir su trouver un principe réduisant la dynamique à une science de l'équilibre et permettant la résolution ou mise en équation de tous les problèmes de mécanique (Mécanique analytique, 1788). Chez D'Alembert, les mouvements perdus ou gagnés par le biais des liaisons mécaniques s'équilibrent et ils définissent, en application du principe, l'équation déterminant la solution du problème. Lagrange procède différemment. Il reproche la complexité de l'application du principe qui ne peut faire l'impasse sur l'examen des figures et sur l'habileté du géomètre dans la détermination de cette équation des mouvements équilibrés. Aussi, au lieu de s'attacher aux mouvements perdus ou gagnés, Lagrange en prend d'autres équivalents. Puisque le mouvement détruit est la différence entre celui imprimé et l'effectif, il s'attache à l'équilibre entre les imprimés et les effectifs pris en sens contraire : en supposant F un ensemble de forces imprimées à un système et F' un autre ensemble qui communiquerait aux corps supposés libres du système les mouvements réels qu'ils prennent à cause des liaisons, l'action simultanée de F et – F' conduit à un équilibre. Indéniablement, le livre de Lagrange dont l'influence sera considérable au 19ème siècle s'appuie sur le Traité de D'Alembert, tant sur son principe que sur l'ambition de fonder rationnellement la mécanique. Cependant, il n'en garde pas l'esprit, à savoir la critique de concepts dynamiques, Lagrange considérant la force comme première et non seulement comme une simple définition mathématique.
|
Figure 4
 Joseph-Louis Lagrange (1736-1813)
Dès la fin
des années 1750, le jeune savant turinois est
considéré comme le mathématicien le
plus
prometteur de la nouvelle génération. Il devient
vite
l'ami de D'Alembert, ave lequel il échange une
correspondance
d'un quart de siècle. Une grande partie de l'oeuvre tardive
de
D'Alembert peut-être considérée comme
une sorte de
discussion scientifique avec Lagrange.
|
Mais au fond, le projet dalembertien d'épurer la mécanique de toute approche causale tient-il toutes ses promesses ? La démonstration des principes repose sur celui de raison suffisante. Son usage constitue la pierre d'achoppement de l'édifice car comment critiquer de manière cohérente l'axiome de proportionnalité des effets à leurs causes alors même que ce principe de raison revient à signifier qu'il ne peut y avoir d'effet sans cause, que rien n'arrive sans raison ? D'Alembert semble s'en remettre à l'évidence, au bon sens, dans son usage d'un principe qui ne respecte pourtant pas les critères de clarté anti-métaphysiques qu'il prône. D'autre part, comment, à lui seul, ce principe abstrait saurait déterminer une grandeur invariante (la quantité de mouvement dans le cas du principe de l'inertie) ? De nombreux commentateurs (H. Poincaré, La Science et l'hypothèse ; E. Meyerson, Identité et réalité, 1908) ont attiré l'attention sur ce problème : le principe de raison est une coquille vide que seule l'observation peut compléter dans la détermination de la grandeur conservée en question. En somme, le projet d'élaborer une mécanique déductive est grevé par une approche empirique qui s'ignore. Mais il n'est pas si sûr que D'Alembert s'y trompe ; il reviendra à de nombreuses reprises dans ses Opuscules mathématiques sur les démonstrations du principe d'inertie et de la composition de mouvement, faits témoignant sans doute d'une insatisfaction. Des successeurs et disciples ne s'y tromperont pas non plus. Ainsi, Lazare Carnot, fidèle à la posture dalembertienne d'une critique de la force, affirmera pourtant le caractère empirique des lois de la mécanique (Principes généraux de l'équilibre et du mouvement, 1803). En somme, par sa critique des fondements de la mécanique de D'Alembert, Carnot se ferait plus dalembertien que le maître.
Conclusion
D'Alembert entend par son Traité de dynamique clarifier les fondements d'une science, tant sur le plan scientifique que philosophique. Il vise à conférer à la mécanique le même degré de certitudes qu'ont les mathématiques et déduit rationnellement des concepts premiers d'espace, de temps, de matière –qualifiées de notions "naturelles"- les lois (ou principes) du mouvement qui donnent naissance au "principe général" apte à résoudre tous les problèmes de dynamique (collisions, système à liaison). L'ambition de réfuter les débats philosophiques liés à une approche causale de la mécanique se manifeste par un rejet de concepts porteurs d'un sens autre que scientifique ; ainsi, la force ne devient que le nom d’un effet mathématisé. Ce projet remarquable et salutaire de l'œuvre se voit contrebalancé par la volonté d'établir rationnellement la mécanique, science qui ne peut faire l'impasse sur des acquis empiriques. Ce livre reste cependant un monument dans l'histoire de la pensée, une aventure intellectuelle considérable comme seuls quelques génies des sciences surent l'entreprendre. Et s'il n'avait écrit que ce livre, D'Alembert occuperait déjà une bonne place dans ce panthéon.
|
|