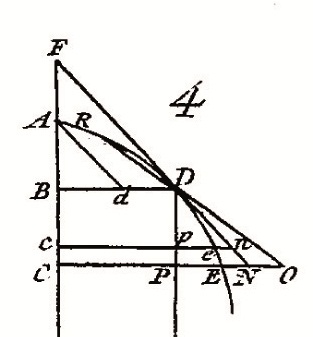
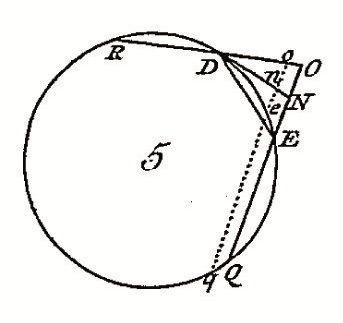
Soit la courbe ADE, avec BD et CE les espaces parcourus pendant des durées AB et AC (Cf. Figure 4 ci-dessus). Si le corps continuait son mouvement avec sa vitesse en D, il parcourait pn et PN pendant deux temps infiniment proches Bc, BC ; mais sous l'action d'une "cause étrangère", il parcourt réellement les espaces ne et NE pendant ces durées. En supposant les temps "infiniment petits", D'Alembert assimile l'arc DE à l'arc de cercle du même nom sur la Figure 5 (ci-dessus), Dn et DN étant des "portions infiniment petites" de la tangente au cercle en D. En traçant NQ et nq parallèles et coupant le cercle en E, Q et e, q : NE × NQ = DN² et ne × nq = dn² (propriété géométrique du cercle). NQ et nq "doivent être regardées comme égales" et, ainsi, NE / ne = DN² / Dn² . Or DN / Dn = BC / Bc, il suit NE / ne = BC² / Bc².
Ainsi, "les espaces parcourus par un Corps en vertu d’une puissance accélératrice quelconque, sont au commencement du Mouvement comme les quarrés des tems". D'Alembert pose φ = NE / BC² , une "quantité quelconque" variable ou non en fonction du temps, mais supposée constante si celui-ci varie peu ; il s'agit de la "puissance accélératrice". En prenant dde = NE, dt = BC; il suit φdt² = ± dde (1) (le signe + (resp. -) correspondant à une accélération (resp. décélération)). Avec u = de / dt la vitesse instantanée du corps et en faisant dt constante, on obtient du.dt = dde soit avec (1), φdt= ±du, relation qui définit la "force accélératrice".