CultureMath
Ressources adaptées au programme de mathématiques de terminale S
Le programme des premières S (B.O. 2011) est disponible en version pdf.
Il est découpé en trois grands thèmes (plus deux pour l'enseignement de spécialité), et assorti de deux capacités transversales. Cliquez sur les différents thèmes pour obtenir une liste de ressources CultureMATH correspondantes.
- Analyse
- Géométrie
- Statistique et probabilités
- Arithmétique (enseignement de spécialité)
- Matrices et suites (enseignement de spécialité)
Deux capacités transversales :
Nous affirmons que la technique utilisée notamment par Cauchy pour généraliser l’intégrale de Cauchy pour les fonctions continues (IC1) aux intégrales impropres (I*C1 ou IC2) s’apparente à une technique qui permet d’effectuer un transfert d’un apprentissage. En effet, Jacques Tardif propose la définition minimale suivante d’un transfert d’un apprentissage :
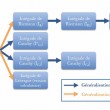
Nous retrouvons au 19e siècle quatre façons de définir ou de comprendre la notion mathématique d’intégrale : l’intégrale de Cauchy, l’intégrale de Riemann et les versions calculatoire et axiomatique de l’intégrale de Lebesgue. Nous proposons d’étudier les généralisations de ces façons de définir l’intégrale en introduisant deux types de généralisations : les généralisations conservatives et les généralisations innovantes. Dans le premier cas, la façon de définir l’intégrale ou de calculer l’intégrale est conservée et son extension est augmentée, c’est-à-dire qu’il y a plus de fonctions qui sont intégrables selon cette façon. Dans ce second cas, la façon de comprendre l’intégrale change et il y a une réinterprétation, voire une reconstruction de la notion.
L'objet principal de ce livre est l'analyse mathématique, plus précisément l'étude des fonctions (explicites ou implicites) à une variable réelle en l'abordant d'un point de vue soit local, c'est-à-dire au voisinage immédiat d'un point, soit asymptotique, c'est-à-dire pour des points situés fort loin de l’origine dans le plan...
Un paradoxe est ce qui défie la raison et semble la mettre en échec. Un paradoxe est ce qui conduit à penser en même temps une chose et son contraire. Un paradoxe est ce qui remet en cause une idée jugée certaine et qui finalement ne l’est certainement pas ! Un paradoxe est une démangeaison, un inconfort mental, une provocation, une obligation faite à l’intelligence de revenir sur elle-même et ses habitudes. Ce livre présente au lecteur cinquante paradoxes sous forme de défis...
Les mathématiciens de la Renaissance et de l'Âge classique étaient convaincus que les anciens géomètres disposaient de méthodes heuristiques qu'ils s'ingéniaient à cacher, se contentant de publier leurs démonstrations synthétiques. Dans le cas d'Archimède et de ses preuves par "exhaustion", il fallait qu'il eût, par avance, une idée du résultat à établir...
Pour voir comment la méthode fonctionne nous nous inspirerons librement de la première Proposition de la Mesure du cercle d'Archimède.
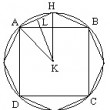
On a un cercle de centre K, de rayon AK. Le triangle rectangle EFG est tel que : EF = AK et la droite EG est égale à la circonférence du cercle.
Nous voulons montrer que le cercle est égal à EFG...
Les démonstrations dites par exhaustion ont une structure logique forte. Elles visent à établir l'égalité de deux figures, F1 = F2 ou l'identité de deux rapports, F1 : F2 :: F3 : F4. Pour ce faire, on fait l'hypothèse que l'on a par exemple F1 > F2 (ou F1 : F2 :: F3 : F avec F > F4) et l'on montre qu'on aboutit à une contradiction...
Archimède de Syracuse est incontestablement le mathématicien grec le plus célèbre et le plus admiré. Il est le seul des géomètres non philosophes à qui l’on ait consacré, dès l’Antiquité, une biographie. Mais ce sont ses prouesses techniques qui furent célébrées, plutôt que ses écrits géométriques. Plusieurs d’entre eux résolvent des problèmes non triviaux de quadrature (segment de parabole, cercle et spirale) et de cubature (sphère et cylindre, sphéroïdes et conoïdes). Ils complètent les travaux d’Eudoxe de Cnide qu’Archimède s’était choisi comme précurseur. Le Syracusain va plus loin lorsqu’il combine mécanique (théorie des centres de gravité) et géométrie mais sa célèbre Méthode, peu diffusée dans l’Antiquité, faillit disparaître.
Le nom du mathématicien allemand Georg Cantor (1845-1918) est notoirement lié à ses travaux sur l’infini, qui ont transformé le fondement des mathématiques dans la deuxième moitié du XIXe siècle. Ce sont d’autres aspects, relativement méconnus ou peu étudiés, qui sont abordés dans cet ouvrage. Établis à partir de la correspondance que le mathématicien échange avec les Français, ils permettent d’appréhender sous un angle nouveau la personnalité d’exception qu’est Georg Cantor, d’éclairer de manière inattendue les différentes formes de son activité.