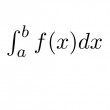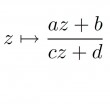CultureMath
[1] Approximation diophantienne et réseaux
[2] Une démonstration originale de l'infinité de l'ensemble des nombres premiers
[3] Sur l'algorithme RSA
[4] Arithmétique
[5] Fermat revisité
[6] Le problème des nombres gelés de Saint-Exupéry
[7] Les mathématiques du mouvement Introduction informelle aux systèmes dynamiques
[8] Petits pièges de la simulation numérique
[9] Le théorème de Sharkovskii
[10] Arbres et dérivée d'une fonction composée
[11] Homographies et suites récurrentes
[12] L'intégration selon Riemann et selon Lebesgue
[13] Signal numérique et théorie de l'échantillonnage
[14] Les intégrales de Coxeter
[15] Equirépartition d'une suite de nombres
[16] Addendum sur l'équirépartition
[17] Racine carrée fonctionnelle
[18] Le lemme de Baire
[19] Le théorème de JUEL et la surface de CLEBSCH
[20] Critères d'Ermakov
[21] Le produit d'Hadamard de deux séries entières
[22] Racine carrée fonctionnelle
[23] Jauge d'une cuve à Mazout
[24] Sur les nombres constructibles
[23] Construction des polygones réguliers
[26] Courbure des surfaces triangulées
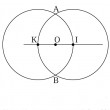
[27] Le problème des 5 cercles
[28] Reconnaître effectivement les Ensembles Algébriques Réels
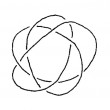
[29] Pour nouer, il faut courber
[30] Autour des triangles inscrits sur une hyperbole équilatère
[31] Gaspard Monge, de la planche `a dessin aux lignes de courbure
[32] Loi de groupe dans un triangle
[33] Les épi ou hypo trochoïdes
[34] Géométrie sur une Strophoïde
[35] Fermeture Hexagonale
[36] Cubiques circulaires passant par leurs foyers singuliers
[37] Combien de fois faut-il battre un jeu de cartes ?
[38] Avant le référendum
[39] La percolation
[40] Processus de branchement et descendance d'un individu
[41] Marches aléatoires sur Z
[42] Le jeu de Pile ou Face
[43] Le Berlekamp's switching game
[44] Jeux sur les graphes et théorème de Ramsey
[45] Jeux et stratégies
[46] Equations algébriques
[47] Intégration de polynômes, points de Gauss
[48] Les tonalités musicales vues par un mathématicien
[49] Loi de groupe sur une surface
[50] La transformation du Boulanger
[51] Rubik’s cube, groupe de poche
[52] Compte de rebonds
[53] La toupie Tippe-Top
[54] Détermination du sexe selon la température chez les crocodiles
[55] Calcul Tensoriel. Application à la relativité.
[56] Equations de Maxwell et formes différentielles, vers la relativité restreinte
[57] Les motifs des pelages d’animaux
[58] Les cercles de Tücker
[59] Interactions entre espèces, modèle de Lotka-Volterra
[60] Équation de la chaleur : traitement numérique
[61] Simulation numérique de l'équation de la chaleur
[62] Du bruit dans les images
[63] Image and movie denoising by nonlocal means
[64] Construction des entiers naturels
[65] Les axiomes de Zermelo-Fraenkel
[66] Entiers relatifs
[67] Nombres rationnels
[68] Nombres réels
[69] Nombres complexes
[70] Quaternions
[71] Ordinaux
[72] La construction des Réels par les coupures de Dedekind
[73] Laplace, Turing et la géométrie impossible du "jeu de l'imitation"
[74] La divination sikidy à Madagascar
[75] Les généralisations de la notion mathématique d'intégrale au 19e siècle
[76] Le processus d'abstraction dans le développement des premières théories de la mesure
[77] Les deux premiers journaux mathématiques français: les Annales de Gergonne (1810-1832) et le Journal de Liouville (1836-1845)
[78] Pourquoi, pour qui enseigner les mathématiques? Une mise en perspective historique des finalités et des contenus de l'enseignement des mathématiques dans la société française au XXe siècle.
[79] Les matrices : formes de représentation et pratiques opératoires (1850-1930)
[80] La loi des grands nombres, le théorème de De Moivre-Laplace
[81] La formule de Stirling
[82] Urnes aléatoires, populations en équilibre et séries génératrices
[83] Zeta de 3 est irrationnel
[84] Généalogie de populations : le coalescent de Kingman
[85] Cantor et la France
[86] Introduction à la Théorie des Groupes
[87] À la recherche de la genèse du dernier mémoire mathématique de Georg Cantor
[88] Le triangle: philosophie, histoire, mathématiques
[89] Au menu: de la géométrie à toutes les sauces
[90] Gaston DARBOUX : « Principes de Géométrie Analytique »
[91] "Souvenirs sur Sofia Kovalevskaya" de Michèle Audin
[92] Eléments d'analyse et d'algèbre (et de théorie des nombres)
[93] Pourquoi les mathématiques sont-elles difficiles ?
[94] Souvenirs sur Sofia Kovalevskaya - interview/discussion avec Michèle Audin
[96] Analyse mathématique - La maîtrise de l'implicite
[97] Epistémologie mathématique
[98] Galois, le mathématicien maudit
[99] Les Clefs pour la PSI et la PSI*
[100] Blagues mathématiques et autres curiosités
[101] Escapades arithmétiques
[102] Le jardin des courbes - Dictionnaire raisonné des courbes planes célèbres et remarquables
[101] Le problème de l'espace. Sophus Lie, Friedrich Engel et le problème de Riemann-Helmholtz
[102] Riemann : Le géomètre de la nature
[103] Eléments d'analyse et d'algèbre (et de théorie des nombres) (présentation par l’auteur)
[104] La construction tractionnelle des équations différentielles
[105] Géométrie analytique classique
[106] La passeggiata - Battements d'ailes au jardin du Luxembourg
[107] Vers une nouvelle philosophie de la nature
[108] Probabilités et statistiques aujourd'hui
[109] Des Mathématiciens de A à Z
[110] Souvenirs sur Sofia Kovalevskaya (parutions)
[111] Cantor et la France
[112] Dimensions
[113] Arithmétique
[114] La correspondance entre Henri Poincaré et les physiciens, chimistes et ingénieurs
[115] Premiers cours de philosophie positive
[116] Une Introduction à la théorie des nombres
[117] Outils mathématiques à l’usage des scientifiques et ingénieurs
[118] Nombres : Eléments de mathématiques pour philosophes
[119] Images des Mathématiques 2004-2006
[120] Leçons de mathématiques d'aujourd'hui
[121] Zoom sur les métiers des mathématiques
[122] Autour du centenaire Lebesgue
[123] L'épistémologie : état des lieux et positions
[124] Philosophie naturelle et géométrie au XVIIe siècle
[125] Les Mathématiques dans la Cité
[126] Réduction des endomorphismes
[127] Les femmes et l'enseignement scientifique
[128] Exercices de mathématiques pour physiciens
[129] La Relativité de Poincaré de 1905
[130] L'espace physique entre mathématiques et philosophie
[131] Jacques Hadamard, un mathématicien universel
[131] Un mathématicien d'exception
[132] Nouvelle bibliographie cournotienne
[133] Paul Painlevé (1863-1933). Un savant en politique
[134] La naissance de la théorie de l'information ou la force d'une idée simple
Quand on découvre les mathématiques, on étudie des formes et des nombres. Une manière usuelle d'associer des nombres à une forme est de mesurer des longueurs. Ce texte nous présente de façon intuitive les notions de courbure et de torsion des courbes et des surfaces, et présente un théorème classique sur la courbure des nœuds...
Dans un article de 1950, devenu justement célèbre, Alan Turing propose, en vue d'opérer une comparaison fonctionnelle entre le cerveau et la machine, un jeu qu'il appelle "jeu de l'imitation". Cet article fut un pas décisif dans le domaine de la philosophie de la connaissance.
Le texte que nous vous proposons présente un point de vue cognitif sur la question de la différence entre la pensée humaine, continue, et le fonctionnement d'une machine à états discrets.
Ce texte est une présentation systématique de deux théories de l'intégration : celle de Riemann et celle de Lebesgue. Ces deux cadres sont décrits par le menu, ainsi que les résultats les plus marquants (le plus souvent sans démonstration). L'objectif de ce texte est de servir de référence rapide pour la lecture d'autres textes, ou pour avoir une idée d'ensemble de ces théories sans devoir se plonger dans les détails les plus techniques, ou acquérir au prélable trop de connaissances abstraites.
Il est ici question d'un théorème peu connu de G. Polyà, résultat qui fournit une méthode systématique pour dénombrer les coloriages possibles d'un ensemble sous l'action d'un groupe. De tels problèmes peuvent être posés de façon extrêmement simple : par exemple, combien peut-on faire de colliers différents si l'on dispose de 10 perles noires et de 3 perles rouges ?
Depuis l'antiquité grecque, l'un des problèmes les plus fameux en mathématiques est de savoir quels sont les figures, et de manière plus générale les nombres que l'on peut construire à la règle et au compas, partant de deux points du plan qui définissent l'unité de longueur. Les réponses à ces questions sont désormais assez complètes, mais il a fallu attendre plus de deux millénaire pour cela.
Comment gagner à coup sûr au jeu de Nim ? Peut-on gagner à coup sûr aux échecs ? Ou bien est-ce qu'au contraire deux ordinateurs infiniment puissants jouant l'un contre l'autre aboutiraient nécessairement à une partie nulle ? Toutes ces questions tournent autour de la notion de stratégie, le jeu de Nim comme le jeu d'échecs étant des jeux à deux joueurs, finis.
On apprend à tous les étudiants en mathématiques comment étudier une suite récurrente définie par une homographie : on cherche les points fixes de l'homographie, puis on définit une autre suite à l'aide de la première, en distinguant le cas où l'homographie a un point fixe double, et cette suite se révèle miraculeusement être une suite géométrique ou arithmétique...
Les processus de branchement sont des modèles introduits pour étudier le développement d'une population, dans laquelle les individus se reproduisent indépendamment les uns des autres, et selon la même loi de probabilité. Introduit au 19ème siècle pour étudier la probabilité d'extinction de noms de familles illustres en Grande Bretagne, le modèle de Galton-Watson et ses variantes trouve de nombreuses applications en biologie ou en physique nucléaire.
Ce texte est une introduction rapide aux problématiques qui se posent aux mathématiciens qui s'intéressent à la biologie. Partant d'une interrogation légitime ("Les maths peuvent-elles être efficaces en biologie ?"), il se concentre ensuite sur la description d'un exemple d'application intéressante, la modélisation du chimiotactisme chez certaines amibes, montrant à la fois l'intérêt du langage mathématique, et les difficultés qu'on peut avoir pour résoudre un problème aussi complexe qu'un problème de biologie.
Peut-on calculer l'intégrale d'une fonction (sur l'intervalle [0,1] par exemple) si l'on ne connaît que sa valeur en 3 points ? Évidemment non, sauf si l'on sait en outre qu'il s'agit d'un polynôme de degré 2 ! Facile, me direz vous : dans ce cas, la donné des valeurs en trois points, quels qu'il soient, permet de retrouver le polynôme et donc de calculer cette intégrale. Beaucoup plus fort : si l'on choisit correctement ces trois points, on peut calculer l'intégrale de n'importe quel polynôme de degré 5, en ne connaissant que sa valeur en nos trois points. Et cette fois, plus question de trouver le polynôme.