Article déposé le 09/04/2012. Editeur : Eric vandendriessche. Toute reproduction pour publication ou à des fins commerciales, de la totalité ou d'une partie de l'article, devra impérativement faire l'objet d'un accord préalable avec l'éditeur (ENS Ulm). Toute reproduction à des fins privées, ou strictement pédagogiques dans le cadre limité d'une formation, de la totalité ou d'une partie de l'article, est autorisée sous réserve de la mention explicite des références éditoriales de l'article. 

1. L'Encyclopédie

Le "Discours préliminaire", la préface du tome III, les Eloges de Montesquieu et de Dumarsais, l'article "Collége" où est critiqué l'enseignement de l'époque, l'article "Dictionnaire" où sont dégagés les différents types de ces ouvrages et leurs objectifs, l'article "Genève" et ses scandales sur la religion et sur les spectacles. Telles sont les contributions que l'histoire a souvent mises en avant quand il s'est agi de D'Alembert et de l'Encyclopédie. Certes, on ajoute en général que ce savant était responsable des articles de mathématiques, que ces derniers étaient remarquables, mais c'est en général pour ne pas évoquer leur contenu ... Or D'Alembert a signé environ 1700 articles, dont 90 % d'articles scientifiques parmi lesquels 90 % concernent les mathématiques au sens large, c'est-à-dire comprenant la mécanique, l'hydrodynamique, l'acoustique, l'astronomie, l'optique. C'est à ces derniers qu'est consacré ce chapitre. Mais un petit rappel s'impose, afin d'éviter les contresens.

Figure 1 Frontispice de l’Encyclopédie, représentant le "couronnement de la vérité", dessiné par Charles-Nicolas Cochin et gravé par Bonaventure-Louis Prévost, 1772.

2. Un ouvrage atypique

Le mot "encyclopédie" évoque pour nous un ouvrage, plus souvent collectif qu'individuel, bien structuré, possédant une unité de ton et de forme. La place d'un article dans l'ordre alphabétique a peu d'incidence sur son contenu. On a décidé au départ, une fois pour toutes, si on mettait ou non des noms de personnes, des noms de lieux, on a pris un parti sur l'équilibre des volumes et sur leur économie générale, sur l'articulation entre les "entrées" des grandes disciplines scientifiques (mathématiques, physique, chimie, etc.), celles de leurs sous-disciplines (algèbre, géométrie, analyse, etc.), celles des termes plus spécifiques (droite, plan, ellipse, cycloïde, etc.). La liste des articles est même quasiment arrêtée dès le début. Le volume 1 ressemble comme un frère au volume 10.

Rien de tout cela dans l'Encyclopédie de Diderot et D'Alembert: le tome I ne ressemble pas au tome VII, lequel se situe sur une autre planète que le tome XVII. Ce fait est connu dans l'abstrait, mais on l'oublie souvent quand on étudie comment l'ouvrage traite une discipline particulière.

Les causes de ce processus chaotique qui rejaillit autant sur les sciences que sur le reste sont à rechercher bien sûr dans l'histoire mouvementée de l'entreprise, de ses interdictions, des changements de libraires-imprimeurs, mais cela n'explique pas tout et notamment pas l'hétérogénéité qui règne à travers les tomes dans les mathématiques et la physique.

A l'origine, il ne s'agissait que de traduire en français et d'adapter, de corriger, d'augmenter, de franciser la Cyclopaedia de Chambers (1728). Sous la houlette de l'abbé de Gua, puis de D'Alembert et de Diderot, on recrute des collaborateurs en nombre assez réduit pour chaque grande discipline, on distribue à chacun une traduction des articles de Chambers correspondant à leur domaine, en leur donnant comme consigne soit de laisser le texte tel quel, soit de le modifier ou de le compléter, soit d'en écrire un autre. C'est dans cet esprit qu'est publié le tome I (1751).

Mais il y a le succès (et la première interdiction de 1752 ne fait que l'augmenter) et les personnalités des deux co-directeurs. En plus de leurs attaques, voilées ou non, vis-à-vis de certains aspects de l'ordre établi, Diderot et D'Alembert ont chacun une certaine idée (un peu différente) des sciences. Le premier est très versé dans les "arts" (lire les techniques) et développe une réflexion philosophique à cet égard. Le second est un savant mathématicien qui a réfléchi à la physique; de plus il est en concurrence et assez brouillé avec les plus grands savants de son temps: Euler, Clairaut, Daniel Bernoulli. Il a aussi des relations conflictuelles avec les académies de Paris et de Berlin: l'Encyclopédie va alors lui servir de lieu de publication pour des idées toutes nouvelles (qu'on réserve habituellement à des mémoires académiques) et d'instrument pour ses querelles. Or la recherche en cours et les polémiques, ça n'attend pas: l'Encyclopédie étant ordonnée par l'alphabet au rythme régulier d'une ou deux lettres par an, si D'Alembert a un compte à régler avec l'un de ses nombreux adversaires, il trouvera bien, dans le volume de l'année, un mot plus ou moins artificiellement lié au sujet, où il peut marquer sa priorité, relever une faute de son adversaire, voire donner un développement qu'il estime intéressant et qu'il n'a pas l'occasion de publier ailleurs.

On peut par exemple traiter des lois du choc à "Choc", à "Communication du mouvement", à "Dureté", à "Elasticité" ou à "Percussion", voire au lieu de naissance de l'un des nombreux savants qui sont intervenus sur le sujet. Il en est de même pour les fluides qu'on peut examiner à ce mot, aussi bien qu'à "Hydrodynamique", à "Pression" ou à "Résistance" ... Les observations plus ou moins acides que D'Alembert écrit sur Euler ou D. Bernoulli peuvent même être égrenées en feuilleton sur plusieurs lettres de l'alphabet.

3. Phase montante et phase descendante

Nous avons dit plus haut que l'Encyclopédie rencontre, notamment du tome III jusqu'au tome VII, un succès croissant qui étonne même ses directeurs. Par un double processus, ce succès a des retombées importantes sur le contenu des articles en général et des articles scientifiques en particulier. D'une part, écrire dans l'Encyclopédie devient un honneur et les contributions spontanées ou à peine sollicitées affluent, tant de la part d'auteurs peu connus que des plus grandes célébrités du siècle (Turgot, Voltaire, Quesnay ...). D'autre part, Diderot et D'Alembert, assez indépendamment l'un de l'autre, recrutent des spécialistes, de façon durable ou ponctuelle. Donnons quelques exemples de cette quête de nouveaux collaborateurs en mathématiques et en physique. Lorsque D'Alembert voit passer à l'Académie des sciences un mémoire intéressant, il propose souvent à l'auteur de rédiger un article sur des questions analogues pour l'Encyclopédie. Ceci est particulièrement vrai pour les tomes V-VIII, correspondant aux lettres E-F-G-H, qui occupent d'ailleurs ici davantage de place que leur proportion dans un dictionnaire usuel (21 % contre 16 %). Ainsi D'Alembert recrute-t-il de Ratte, secrétaire de la Société royale des sciences de Montpellier, lequel rédige "Froid", "Gelée", "Gelée blanche", "Givre", "Glace" "Grêle" (t. VII) et "Neige" (t. XI). Ainsi de l'article "Frottement" (t. VII) de Louis Necker, qui suit de peu un mémoire présenté par l'auteur à l'Académie sur le même sujet. Ainsi des articles de Rallier des Ourmes "Echelles arithmétiques", "Escompte" (t. V), "Exposant" (t. VI), "Fraction" (t. VII), "Huit", "Impair", "Intérêt" (t. VIII), "Neuf", "Onze", "Pair" (t. XI), "Permutation" (t. XII), "Progression", "Proportion" (t. XIII): l'auteur venait d'envoyer un mémoire à l'Académie sur les carrés magiques, dont D'Alembert a dû être content.

Nous avons parlé jusqu'ici de la "phase ascendante" de l'Encyclopédie, celle qui va du tome I (1751) au tome VII (1757), c'est-à-dire de la lettre A à la lettre G, au rythme d'un volume par an. Quand surviennent la brouille entre Diderot et D'Alembert (1758), puis l'interdiction de l'ouvrage (1759), la lettre H est quasiment prête. Malgré la crise et les hésitations, les volumes suivants se préparent petit à petit, mais les dix derniers tomes VIII-XVII ne paraissent (ensemble) qu'en 1765. C'est en quelque sorte la "phase descendante". D'Alembert a réduit sa participation aux seules mathématiques et à un peu de physique, et même pour ces disciplines son investissement est moindre. D'autre part, l'essentiel de la rédaction est assurée par le chevalier de Jaucourt, auteur certes très instruit et remarquable, mais qui ne peut avoir le génie des plus grands auteurs du siècle, chacun dans son domaine. En outre, dans les derniers volumes, on sent bien que tout le monde est pressé d'en finir. Il n'est donc pas étonnant que, globalement, les derniers tomes soient scientifiquement moins toniques que ceux du milieu. Ils restent cependant intéressants et surprenants à bien des égards, et tout aussi hétérogènes que les précédents. Tous les prétextes sont bons pour réparer les oublis ou pour placer telle ou telle idée là où personne ne l'attendrait. Par exemple, on insère des biographies de personnages, voire des théories scientifiques qui leur sont dues ou des remarques politiques sur leur vie, au nom de leur lieu de naissance. Aux derniers tomes, le chevalier de Jaucourt fait même une orgie de ce stratagème. On trouve par exemple de Moivre à l'article "Vitri-le-François", il s'agit d'ailleurs surtout de dénoncer le scandale et la catastrophe nationale de la Révocation de l'Edit de Nantes, en prenant appui sur le fait que le protestant de Moivre a dû alors fuir en Angleterre. On trouve aussi les lois de Hooke à l'article "Wight" ou un panorama des travaux de Newton à "Wolstrope".

Figure 2 Louis de Jaucourt (1704-1779)

4. Les "Discours" et les "Planches"

Nous ne sommes pas au bout de notre étonnement. Quel a pu être l'impact des articles de mathématiques ou de physique sur le public au milieu du XVIII^e siècle ? Il a vraisemblablement été limité, il y a à cela plusieurs raisons. D'abord l'ordre alphabétique n'est pas forcément le mieux adapté pour un lecteur qui voudrait se cultiver dans une science particulière, sauf de façon ponctuelle. En mathématiques, en physique, en chimie, on a en général besoin d'une certaine progression méthodique de la connaissance. L'hétérogénéité des articles, ici quelquefois franchement délirante, amplifie encore la difficulté à naviguer efficacement entre les entrées, surtout avant que la Table du pasteur Mouchon ne soit publiée (1780). Un bon manuel est plus commode que l'Encyclopédie (et moins cher) pour apprendre l'algèbre ou l'optique.

Dans certains cas, il existe une autre raison qui rend même impossible la lecture des articles. Essayez de lire l'article "Conique" (t. III, 1753), si vous ne savez pas déjà ce que c'est: cet article fait appel dès le début à des figures de mathématiques, mais les planches correspondantes ne sont publiées qu'en ... 1767. Le même phénomène est encore plus criant pour la description d'instruments de mathématiques, d'optique ou d'astronomie.

Figure 3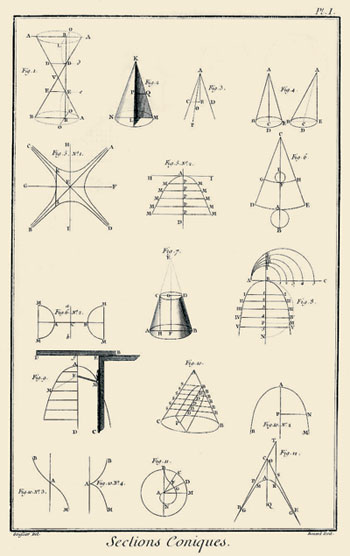 Cliquer sur l'image pour l'agrandir Planche associée à l'article "Conique" de l'Encyclopédie: elle parut en 1767, soit 14 ans après l'article qu'elle illustrait ...

5. Surprendre D'Alembert avec sa colle et ses ciseaux

Au moment de la mise en place de l'aventure encyclopédique, D'Alembert se voit confier, comme nous l'avons dit, les mathématiques pures et mixtes, ainsi que la physique générale. Mais la chimie (surtout traitée par Malouin, puis par Venel et d'Holbach), l'anatomie (Aumont), l'histoire naturelle (Daubenton), l'art militaire (Le Blond), ne sont pas chapeautés par lui. Pour les mathématiques élémentaires, D'Alembert a sous-traité le gros-œuvre à un personnage intéressant, auteur de manuels d'enseignement novateurs, l'abbé de La Chapelle, qui signe par la marque (E), et il s'est gardé pour lui-même les mathématiques plus "transcendantes" ainsi que les réflexions métaphysiques sur cette discipline (voir Encart 2). Nous avons plus haut surpris D'Alembert au téléphone en train de recruter des collaborateurs; nous allons maintenant le surprendre avec la colle et les ciseaux, en d'autres termes, nous allons dire un mot de la façon (des façons) dont il a composé ses "propres" articles, en principe signés (O).

D'Alembert pratique comme les autres: souvent il se contente de reproduire la traduction de Chambers ou de laisser La Chapelle faire de même. Il y ajoute de temps à autre un commentaire sur les fondements ou sur le sens philosophique du concept, ou un développement de travaux plus récents. Dans d'autres cas, comme nous l'avons dit, en mathématiques, notamment sur le calcul différentiel et intégral, en mécanique ou en hydrodynamique, certains articles sont en fait de vrais mémoires de recherche. Ces remarques, pour vraies qu'elles soient, ne doivent pas nous conduire à croire que les mathématiques de l'Encyclopédie ne seraient que du "bricolé". D'Alembert a quand même largement pensé ces centaines d'articles dans leur ensemble, les a ordonnés et hiérarchisés entre eux. Et comme il n'a jamais rédigé de traité de mathématiques pures, certains longs articles comme "Cas irréductible", "Différentiel", "Equation", etc. représentent une mise au point remarquable sur des sujets assez larges; on peut même dire qu'une lecture judicieuse (dans un ordre à trouver soi-même !) de plusieurs dizaines d'entre eux constituerait un traité d'algèbre original. En revanche, en ce qui concerne l'astronomie, il faut bien distinguer deux aspects: l'utilisation des mathématiques pour l'étude du mouvement des astres et l'astronomie classique d'observation. En mécanique céleste, D'Alembert a été créatif et ses articles rendent compte de ses travaux, ainsi que de ceux de certains de ses contemporains (à sa manière, certes); mais en astronomie d'observation, il se contente un peu du "service minimum" et s'appuie assez tranquillement sur les Institutions astronomiques de Le Monnier, auxquelles il renvoie souvent. Il n'est donc pas étonnant que cela ne plaise pas à Lalande, qui va refaire à peu près tout, quelques années plus tard, dans le Supplément et la Méthodique.

Il faut aussi se souvenir que les éditeurs de l'Encyclopédie ont acheté un grand nombre de textes à Formey, savant de l'Académie de Berlin et qu'ils les éparpillent à divers endroits lorsqu'ils en ont besoin; ils utilisent aussi des dictionnaires antérieurs comme Wolff et Harris. Cela dit, pour l'essentiel, les articles de physique générale constituent ouvertement un pillage en règle des Elémens de physique de Musschenbroeck. En fait, près d'une moitié de ce remarquable traité se trouve découpé en morceaux tout au long de l'Encyclopédie: tantôt D'Alembert saute un paragraphe, enlève un exemple, tantôt il en ajoute un ou donne un commentaire, et il termine invariablement par une phrase du genre: "Ceci est extrait à peu près de M. Musschenbroeck". Ainsi donc, le physicien de Leyde est-il l'auteur de la presque totalité de la physique de l'Encyclopédie sans figurer dans aucun inventaire des auteurs.

6. La suite du processus

La participation de D'Alembert aux suites de la grande encyclopédie est infinitésimale. Il donne certes quelques articles pour le Supplément (1776-77), mais sa contribution est modeste. Plus tard, l'Encyclopédie méthodique - Mathématiques (1784-89) reprend ses anciens articles, mais D'Alembert, qui meurt d'ailleurs au moment de sa préparation, ne peut tenir sa promesse d'ajouter quelque chose de nouveau. Néanmoins, ses contributions antérieures sont rééditées en divers lieux, et en outre ses deux disciples préférés, Condorcet et Bossut, prennent une part active au Supplément ou à la Méthodique: on peut donc affirmer que son esprit se diffuse au-delà de l'arrêt de sa participation massive, laquelle se termine en 1762.

La part de D'Alembert à l'Encyclopédie est donc très variée. En plus de son rôle irremplaçable dans la mise en route de l'entreprise, dans ses orientations fondamentales, il donne une vie incroyable aux sciences mathématiques et physiques, mais l'imprévu et quelquefois la désinvolture ont eu de quoi dérouter le lecteur et la réception à moyen terme en a pâti.