1. Introduction
A la fin du XVIIe siècle, les sciences - et particulièrement les mathématiques - ont connu une grande révolution : l'invention du calcul différentiel et intégral par Newton et Leibniz. Peu après son émergence dans les années 1684-1687, cet outil a permis de résoudre une foule de problèmes physiques et géométriques. Les décennies qui ont suivi ont donc été marquées par un avancement et une progression rapides dans beaucoup de domaines. La période à laquelle D'Alembert débute sa carrière scienti fique est en revanche plus une période de stabilisation des acquis et de mise à l'épreuve de ceux-ci. Les ruptures sont bien moins nettes. Néanmoins, le développement du calcul différentiel et intégral a encore des répercussions, notamment en algèbre, de façon indirecte, concernant la théorie des équations algébriques.
Connu sous le nom de théorème de D'Alembert-Gauss, le théorème fondamental de l'algèbre, aujourd'hui familier des étudiants, affir rme que tout polynôme réel a au moins une racine réelle ou imaginaire (Encart 1). Dès le début du XVIIe siècle, Albert Girard et René Descartes écrivent que toute équation algébrique de degré $n$ admet $n$ racines réelles ou imaginaires. Toutefois, cet énoncé ne prend le sens qu'on lui connaît qu'au XVIIIe siècle et les mathématiciens ne s'accordent sur la validité de ce résultat qu'au milieu du siècle. A la même époque apparaissent les premières ébauches de preuves rigoureuses.
Ce changement progressif de perspective est dû à l'évolution du statut des nombres dits imaginaires entre le début du XVIIe et le XVIIIe siècle. Ces nombres sont d'abord vus comme des quantités paradoxales, apparaissant dans la résolution d'équations algébriques particulières : la racine carrée d'un nombre négatif a-t-elle un sens ? Ne risque-t-on pas, avec ces nombres, de se perdre dans les multiples écritures d'un même nombre (Encart 1) ? Dans les années 1740, cette seconde question va être tranchée grâce à D'Alembert. Mais pourquoi le savant s'intéresse-t-il à ces nombres ?
2. Du calcul intégral aux imaginaires
Bien que le théorème fondamental de l'algèbre soit considéré de nos jours comme un résultat d'algèbre, les motivations qui ont poussé les mathématiciens à rechercher une preuve digne de ce nom du théorème fondamental se situent du côté du calcul intégral. Dans un mémoire sur l'intégration des fractions rationnelles, Leibniz s'interroge en 1702 sur la possibilité ou non de décomposer le polynôme au dénominateur de celles-ci en facteurs réels du premier ou du deuxième degré [1]. Euler est confronté au même problème en 1739 dans le cadre de l'intégration des équations différentielles linéaires d'ordre $n$, qui fait apparaître des polynômes de degré $n$. Contrairement à Leibniz, il tranche la question positivement sans toutefois proposer de preuve. D'Alembert, pour sa part, s'intéresse au calcul intégral à cause de problèmes de mécanique qu'il examine dans son Traité de dynamique : il étudie le Treatise of fluxions de Colin Maclaurin, se consacre à l'intégration des équations différentielles et dans la lignée de MacLaurin, à la classification et à l'intégration des formes différentielles (rationnelles, irrationnelles...). Il constate vite l'absence de preuve de ce qui deviendra le théorème fondamental de l'algèbre et s'attaque au problème.
Dans un mémoire de 1746, il établit ainsi la stabilité de l'expression $a+b\sqrt{-1}$ par les opérations algébriques usuelles. Il montre en effet que si on ajoute, soustrait, multiplie ou divise des quantités de la forme $a+b\sqrt{-1}$, on obtient encore des quantités de la même forme. Il élargit même cette conclusion à des expressions telles $[a+b\sqrt{-1}]^{(m+n\sqrt{-1})}$. Ce travail marque une étape du point vue de la compréhension de la nature des quantités imaginaires. En confirmant que l'ensemble des quantités de la forme $a+b\sqrt{-1}$ est « clos », D'Alembert invalide une idée sur laquelle reposait la plupart des contestations du théorème fondamental de l'algèbre. A partir de là, un consensus s'établit chez les savants sur le fait que tous les imaginaires sont de la forme $a+b\sqrt{-1}$ (c'est-à-dire sont des nombres complexes selon la terminologie moderne, due à Carl Friedrich Gauss).
Dans le même texte, D'Alembert démontre
la proposition suivante :
« Soit un multinôme
quelconque $x^m+ax^{m-1}+bx^{m-2}+...+fx+g$, tel qu'il n'y ait aucune
quantité réelle qui, étant
substituée à la place de $x$, y fasse
évanouir tous les termes, je dis qu'il y aura toujours une
quantité de la forme $p+q\sqrt{-1}$ à substituer
à la place de $x$, qui rendra ce multinôme
égal à zéro. »
En termes modernes, si un polynôme $P$ n'a pas de racines réelles, il a forcément au moins une racine de la forme $p+q\sqrt{-1}$. Pour accomplir sa preuve, D'Alembert fait appel au développement en séries infinies de la fonction réciproque du polynôme considéré et il montre par l'absurde que $P(x)=0$ a toujours une solution réelle ou de la forme $p+q\sqrt{-1}$. La démonstration de D'Alembert est analytique alors que celle que donne Euler trois ans plus tard en 1749 est plutôt algébrique.
En témoignent certains de ses articles dans l' Encyclopédie, le théorème fondamental de l'algèbre joue un rôle central dans les théories des équations de D'Alembert, bien plus que chez ses contemporains. Selon Christian Gilain, historien des mathématiques et membre du Groupe D'Alembert, ce résultat a chez lui le « statut de théorème d'existence » [2] : il prouve l'existence des racines de tout polynôme.
En 1754, dans son Traité du calcul intégral, Louis Antoine de Bougainville reprend la preuve de D'Alembert de 1746 et en donne une présentation plus claire et didactique. En 1772, lorsqu'il aborde la question du théorème fondamental, Lagrange dit de la démonstration de D'Alembert qu'elle « est très ingénieuse et ne laisse [...] rien à désirer du côté de l'exactitude ». Le savant turinois opte néanmoins pour une stratégie de preuve algébrique et proche de celle d'Euler et, deux décennies plus tard, il se montre plus réservé à propos de la démonstration de D'Alembert.
Quoi qu'il en soit, aucune de ces démonstrations ne pourra rivaliser avec la rigueur de Carl Friedrich Gauss. En 1799, le savant allemand passe au crible les preuves de ses prédécesseurs : Euler, D'Alembert, Lagrange et Foncenex. Il reproche notamment à tous ces savants de supposer a priori l'existence de racines d'un polynôme et de ne discuter que la forme de ces racines. En réalité, cette attaque ne concerne pas la preuve de D'Alembert, qui est une preuve d'existence. Néanmoins, Gauss soulève - à juste titre - quelques lacunes de rigueur chez l'encyclopédiste, certes courantes au milieu du XVIIIe siècle. La preuve de Gauss non seulement pallie ces défauts, mais fonde en partie la représentation géométrique des nombres imaginaires dans le plan complexe.
3. Le problème des cordes vibrantes
La seconde contribution majeure de D'Alembert a trait à l'analyse : l'utilisation couronnée de succès des équations aux différences partielles - équations aux dérivées partielles selon la terminologie moderne - pour résoudre des problèmes physiques. Deux textes de la fin de la décennie 1740 sont emblématiques de ce tour de force : ses Réflexions sur la cause générale des vents de 1746 et ses mémoires sur les cordes vibrantes présentés en 1747 (Encart 2).
Un bref rappel historique sur l'émergence du calcul différentiel est ici utile. Présenté pour la première fois dans des textes de Leibniz (1684-1686) et développé indépendamment par Newton à la même époque, le calcul différentiel et intégral a rapidement montré son efficacité dans le traitement de certains problèmes physico-mathématiques et a connu un succès important. Cependant, dans un premier temps, les savants l'appliquent essentiellement à des fonctions à une seule variable. La différentiation de fonctions à plusieurs variables apparaît à la charnière des deux siècles mais les savants peinent à lui trouver des applications concrètes. En outre, ils ne savent pas résoudre les équations différentielles comportant des différences partielles. Euler se penche d'ailleurs sur la question au cours de la décennie 1730. Il publie quelques mémoires mais s'en désintéresse face aux difficultés évoquées.
Figure 2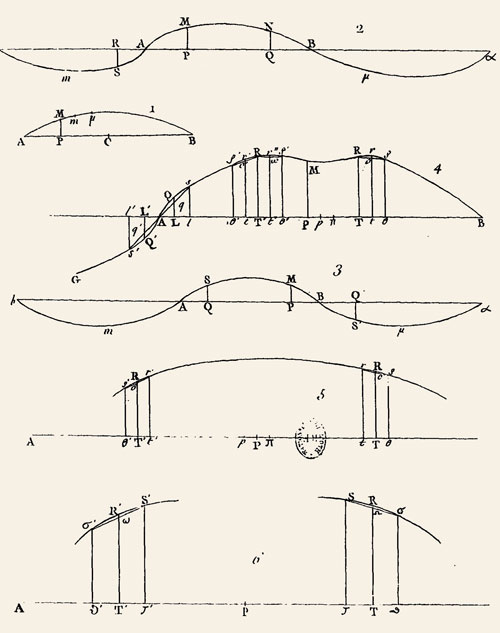 Cliquer sur l'image pour l'agrandir Planche accompagnant le Supplément au mémoire sur les cordes vibrantes |
Dans ses mémoires sur la cause des vents et les cordes vibrantes, D'Alembert parvient à franchir ce cap. Bien entendu, ses études portent sur des situations physiques idéalisées (pas de frottements et diverses autres hypothèses simplificatrices). Néanmoins, grâce à lui, pour la première fois, des équations aux différences partielles décrivent des systèmes physiques et fournissent des solutions. Par exemple, concernant les cordes vibrantes, il établit ce qu'on appelle aujourd'hui l'équation des ondes et montre comment on exprime la fonction $y(t,x)$ donnant la position de chaque point d'abscisse $x$ à chaque instant $t$ en fonction de l'allure de la corde ou de sa vitesse à l'instant initial (Encart 2).
Cette fois encore, Euler n'est pas loin. Dans leur correspondance, il avait déjà montré des réserves sur certains points des travaux de D'Alembert liés au théorème fondamental de l'algèbre ; D'Alembert avait toutefois répondu de manière satisfaisante sur les différents aspects soulevés par le savant suisse. Les deux savants avaient également eu, à la même époque, des divergences sur le logarithme de quantités négatives. Mais, leur affrontement au sujet des cordes vibrantes, et plus particulièrement de la notion de fonction, est bien plus âpre. En 1748, Euler présente un mémoire sur les cordes vibrantes semblable en beaucoup de points à celui de D'Alembert. Toutefois, ce dernier relève une différence d'approche, déclenchant une polémique de plusieurs années.
4. Qu'est-ce qu'une fonction ?
A cette époque, la notion de fonction ne dispose pas de définition précise. Et c'est un désaccord de fond sur cette question qui va conduire les deux savants à s'affronter sur les fonctions que l'on peut admettre comme représentant l'allure initiale de la corde. Selon D'Alembert, dans le contexte du problème des cordes vibrantes, l'expression de cette fonction ne doit pas « changer de forme ». En d'autres termes, conformément aux préjugés de son époque, il interdit les fonctions définies par morceaux et il estime qu'une fonction est avant tout une expression formelle à l'aide de fonctions usuelles (sinus, puissance...) . L'approche d'Euler est moins restrictive, ce dernier n'impose pas de contraintes à l'allure initiale de la corde mise en vibration car il a à l'esprit l'idée qu'une fonction est avant tout une relation de dépendance entre deux variables pouvant s'exprimer de différentes façons. Après avoir donné une première définition de la notion de fonction en 1748, l'étude du problème des cordes vibrantes l'amène ainsi à proposer une définition plus générale en 1755 dans ses Institutiones calculi differentialis :
« Si certaines quantités dépendent d'autres quantités de telle manière que si les autres changent, ces quantités changent aussi, alors on a l'habitude nommer ces quantités fonctions de ces dernières ; cette dénomination a la plus grande étendue et contient en elle-même toutes les manières par lesquelles une quantité peut être déterminée par d'autres. Si, par conséquent, $x$ désigne une quantité variable, alors toutes les autres quantités qui dépendent $x$ de n'importe quelle manière, ou qui sont déterminées par $x$, sont appelées fonctions de $x$. »
Cette définition aura une influence indéniablement positive sur le développement ultérieur des mathématiques. Toutefois, le débat sur les fonctions admissibles dans le cadre du problème des cordes vibrantes, qui bat son plein dans les années 1750, se poursuit au cours des décennies suivantes. D'Alembert, notamment, publie sur le sujet dans ses Opuscules mathématiques à partir de 1761. Ses réflexions et certaines de ses contributions tardives ont été négligées par la plupart des historiens qui ont conclu au triomphe d'Euler sur D'Alembert dans le débat sur les fonctions.
Figure 3 Page de titre des Opuscules mathématiques de D'Alembert |
Dans les tomes I et IV de ses Opuscules,
cherchant
obstinément une réplique à Euler,
D'Alembert développe l'idée qu'une fonction
représentant l'allure initiale de la corde ne doit pas faire
de « sauts de courbure », ce qui
revient
à dire que la dérivée seconde
$\frac{\partial^2y}{\partial x^2}$ doit être continue au sens
moderne. En effet, le terme
« continu » n'a pas au
XVIIIe siècle le sens actuel et désigne les
fonctions ne changeant pas d'expression. La diversité des
arguments donnés par D'Alembert pour interdire les
« sauts de courbure » (calculatoire, physique et
métaphysique) montre bien que les considérations
physiques et mathématiques sont encore intriquées
dans l'approche du savant.
Parallèlement, il continue
à refuser les fonctions définies par morceaux,
qui, pour lui, présentent nécessairement des
« sauts de courbure ». Il ne se
ravise que quelques
années avant sa mort et privilégie dans ses
derniers mémoires une approche de la continuité
plus géométrique, liée à
l'absence de « sauts ». Ainsi, même si
son approche souffre dans un premier temps d'un trop grand attachement
l'expression formelle des fonctions, D'Alembert a contribué
par ses réflexions à propos de la notion de
« saut » à ouvrir la voie à
une définition plus moderne de la continuité,
telle que Cauchy la formulera au début du XIXe
siècle.
Il faut souligner ici que dans ses travaux, D'Alembert a appliqué le calcul aux différences partielles à bien d'autres problèmes que celui des cordes vibrantes. Nous avons évoqué plus haut ses Réflexions sur la cause générale des vents mais nous pourrions également parler de ses recherches sur l'hydrodynamique. Cependant, les considérations sur les fonctions n'apparaîtront que très ponctuellement dans ses mémoires sur ce type de sujet. Elles sont en revanche bien plus présentes dans ses textes sur la propagation du son, sujet très lié aux cordes vibrantes et qui joue un rôle important dans l'évolution tardive de D'Alembert à propos de la notion de fonction...
5. Les séries de Daniel Bernoulli
Un troisième savant éminent intervient dans la controverse sur les cordes vibrantes et les fonctions admises pour décrire l'allure initiale de la corde : Daniel Bernoulli. D'Alembert a déjà ferraillé avec ce dernier sur l'équilibre et le mouvement des fluides ou encore à propos des applications possibles des probabilités.
Quelques années après les premiers mémoires de D'Alembert et Euler, Daniel Bernoulli présente, dans les recueils de l'Académie de Berlin de 1753, un mémoire dans lequel il reproche à ces derniers d'abuser de « l'analyse abstraite » et où il entreprend de donner un « exposé physique des nouvelles vibrations des cordes » proposées par les deux savants. S'appuyant sur la multiplicité des sons qui résonnent derrière le son fondamental lorsqu'on met une corde en vibration - les harmoniques, dirions-nous aujourd'hui -, il affirme que toute fonction représentant l'allure initiale de la corde peut s'exprimer sous la forme :
Son argumentaire est essentiellement physique, ou plus exactement acoustique. Pour lui, chaque fonction sinus représente une vibration harmonique et comme le son émis par la corde est le résultat de la juxtaposition des harmoniques, il suffit de considérer une combinaison linéaire de ces fonction sinus.
Figure 4 Daniel Bernoulli (1700-1782) |
Ainsi, Daniel Bernoulli pense avoir restauré le « sens physique » des vibrations exposées dans les solutions de D'Alembert et Euler. Il affirme en outre que toutes les fonctions envisagées par D'Alembert et Euler peuvent s'exprimer sous la forme d'une combinaison linéaire de ces mêmes fonctions sinus. En écrivant cela, il préfigure des résultats qui ne seront énoncés, puis démontrés qu'au début du XIXe siècle par les mathématiciens Joseph Fourier et Peter Gustav Lejeune Dirichlet.
Aux yeux d'Euler et de D'Alembert, l'ensemble des fonctions
pouvant représenter l'allure initiale de la corde ne peut
pas être englobé dans l'expression
proposée par Daniel Bernoulli, qu'ils jugent trop
restrictive. Les deux savants récusent la
possibilité de développer toute fonction
périodique en séries trigonométriques.
En termes modernes, ils rejettent l'idée que toute fonction
périodique est égale à son
développement en séries de Fourier.
La polémique des cordes vibrantes est également
un terrain sur lequel va se prolonger le débat entre
D'Alembert et Daniel Bernoulli à propos de l'application que
l'on peut faire des probabilités. D'Alembert livre
à cette occasion une critique des travaux de son adversaire
sur les séries divergentes. Dans plusieurs
mémoires, Daniel Bernoulli a tenté d'attribuer
une valeur à des sommes infinies comme $1 - 1 + 1 - 1 ...$
et a proposé de prendre la moyenne des sommes partielles, ce
qui donne dans ce cas $1 - 1 + 1 - 1 ...=1/2$. Il justifie cela en
faisant appel à des arguments de nature probabiliste car,
dans l'exemple envisagé, les sommes partielles valent
alternativement 1 et 0. Fidèle aux critiques qu'il avait
déjà formulées, D'Alembert
considère qu'il y a là une utilisation abusive
des probabilités et rejette en bloc les
égalités obtenues par Daniel Bernoulli avec ce
type de raisonnement...
6. Une œuvre mathématique à part entière
Alors, comment caractériser les mathématiques de D'Alembert ? Existe-t-il un fil conducteur à sa démarche ? Certes, D'Alembert s'est intéressé à des problèmes de calcul intégral à cause de problèmes de mécanique rencontrés dans l'élaboration de son Traité de dynamique. Le lien entre analyse et mécanique est d'autant plus fort qu'au début du XVIIIe siècle, la mécanique est une branche des mathématiques dans la structure disciplinaire académique. Néanmoins, Christian Gilain explique que [3] :
« On n'est pas, ici, dans le schéma d'une fusion entre les domaines, où l'analyse, absorbée par la mécanique, n'interviendrait que pour fournir les outils nécessaires et suffisants pour résoudre les problèmes physiques posés successivement. Ces domaines - analyse et mécanique - ne sont certes pas des champs séparés par des barrières infranchissables, mais ils apparaissent bien, ici, comme des domaines distincts ayant leurs logiques propres, et entre lesquels s'établissent des interactions complexes. »
En outre, l'approche du savant va évoluer au fil du temps. Au cours de la décennie 1760, on le voit encore, dans le cadre de la polémique des cordes vibrantes par exemple, trancher des questions mathématiques avec des arguments de nature physique. Mais par la suite, il adopte une démarche qui va contribuer à l'autonomisation progressive des « mathématiques pures ». En 1768, il est par exemple un des premiers à se lancer dans une étude systématique des équations aux dérivées partielles considérées comme un objet mathématique, hors de tout problème physique. Certes, il est influencé dans cette direction par des savants comme Fontaine ou Condorcet, mais il joue au sein de ce courant un rôle non négligeable sur la fin de sa vie.
La géométrie occupe en revanche une place marginale dans son œuvre mathématique. Au début du XVIIIe siècle, celle-ci est considérée comme plus rigoureuse et pertinente et donc supérieure hiérarchiquement à d'autres champs des mathématiques. La tendance s'est inversée vers le milieu du siècle et D'Alembert accompagne ce mouvement.
Ses mathématiques s'inscrivent donc dans l'air du temps. Quelle empreinte ont-elles alors laissée ? L'influence de D'Alembert sur la génération suivante de savants a souvent été sous-estimée, tout comme l'œuvre tardive de l'encyclopédiste : les fameux neuf tomes d'Opuscules mathématiques. Dans ces ouvrages, D'Alembert soulève régulièrement des questions mathématiques véritablement délicates impossibles à trancher avec les outils de son époque. Ces nombreux points en suspens donnent l'impression que les Opuscules égrènent les doutes et hésitations du savants. Le mode de rédaction n'arrange rien : le savant accumule les réflexions sur des thèmes disparates et publie un volume dès qu'il a atteint un certain nombre de pages. Son style de rédaction, décousu, est souvent rebutant. Aussi ses ouvrages sont-ils peu lus après sa mort. D'ailleurs, dans l'esprit de D'Alembert, ils s'adressent tout au plus à une douzaine de savants susceptibles de les comprendre. Pourtant, ces Opuscules reflètent les échanges et discussions de l'encyclopédiste avec la communauté scientifique à la fin de sa vie et, à ce titre, témoignent de son impact. Dans la seconde moitié de sa carrière scientifique, D'Alembert est en effet un savant respecté et influent. Il marque en particulier trois mathématiciens de renom : Lagrange, Condorcet et Laplace.
En 1759, Lagrange, qui vient de fonder l'Académie des sciences de Turin, entame une correspondance avec D'Alembert qui perdurera jusqu'à la mort de l'encyclopédiste. Affable et peu enclin aux conflits, le savant italien se lie d'amitié avec un D'Alembert qui alors brouillé avec Euler, Daniel Bernoulli et Clairaut. Lagrange accorde une importance certaine aux remarques de D'Alembert sur ses travaux et certains mémoires des Opuscules sont en rapport étroit avec leurs discussions. Dans certaines controverses, comme celles des cordes vibrantes, Lagrange est parfois convaincu par les arguments de l'encyclopédiste et, à l'inverse, des idées de ce dernier transparaissent dans l'œuvre de son correspondant.
Condorcet est encore plus proche de D'Alembert. En 1770, alors qu'il n'a que 27 ans, il accompagne D'Alembert lors de son « voyage en Italie [4]. Secrétaire perpétuel de l'Académie des sciences à partir de 1773 en partie grâce à l'appui de D'Alembert, acteur majeur du Supplément de l'Encyclopédie publié en 1776-1777, Condorcet n'est pas pour autant qu'un disciple de D'Alembert : les deux hommes s'inspirent mutuellement. Partisan d'une étude systématique des objets mathématiques pris hors de tout contexte physique, Condorcet applique cette démarche aux équations différentielles ordinaires et D'Alembert fait de même en 1768 avec les équations aux différences partielles. Condorcet lui emboîte le pas sur le même sujet deux ans plus tard.
Laplace, enfin, n'a que 19 ans lorsqu'il quitte sa province normande pour Paris, en 1768, avec une lettre de recommandation destinée à D'Alembert. Ce dernier est impressionné par ses talents. Laplace devient ainsi le protégé de D'Alembert qui lui trouve un poste de professeur à l'Ecole militaire et le recommande à son tour auprès de diverses institutions. Si Laplace ne partage pas le scepticisme parfois témoigné par D'Alembert à l'égard des probabilités, les questions soulevées par son aîné inspirent ses travaux. Laplace devient ainsi un grand artisan du développement des probabilités. Il emboîte également le pas de D'Alembert sur des sujets tels que la Figure de la terre et les équations aux dérivées partielles. Il ne manque d'ailleurs pas de souligner dans ses mémoires les mérites scientifiques de D'Alembert, même après la mort de celui-ci.
Bibliographie
Pour en savoir plus sur l'œuvre mathématique de D'Alembert et sur les questions évoquées dans cet article :Anne-Marie Chouillet, Pierre Crépel (1994), « Un voyage d'Italie manqué ou trois encyclopédistes réunis », Recherches sur Diderot et sur l'Encyclopédie, p. 9-53.
Alexandre Guilbaud, Guillaume Jouve (2010). "La résolution des équations aux dérivées partielles dans les Opuscules mathématiques de D'Alemberts (1761-1783)", revue d'histoire des mathématiques 15, fascicule 1, p. 59-122.
Christian Gilain (1991). « Sur l'histoire du théorème fondamental de l'algèbre : théorie des équations et calcul intégral », Archive for History of Exact Sciences, 42 (1991), p. 91-136.
Oeuvres complètes de D'Alembert, vol. I/4a, Textes de mathématiques pures (1745-1752), édition établie par Christian Gilain, CNRS Editions, Paris, 2007.
Oeuvres complètes de D'Alembert, vol. III/1, Opuscules mathématiques, tome I (1761), sous la direction de Pierre Crépel, Alexandre Guilbaud, Guillaume Jouve, CNRS Editions, Paris
Notes
[1] Comme le sait tout étudiant de Licence, la factorisation des polynômes joue un rôle important dans l'intégration des fractions rationnelles.[2] Christian Gilain, « Sur l'histoire du théorème fondamental de l'algèbre : théorie des équations et calcul intégral », Archive for History of Exact Sciences, 42 (1991), p. 91-136.
[3] Oeuvres complètes de D'Alembert, vol. I/4a, Textes de mathématiques pures (1745-1752), édition établie par Christian Gilain, CNRS Editions, Paris, 2007.
[4] Anne-Marie Chouillet, Pierre Crépel, « Un voyage d'Italie manqué ou trois encyclopédistes réunis », Recherches sur Diderot et sur l'Encyclopédie, 1994, p. 9-53.
