On appelle, de nos jours, équation aux dérivées partielles (EDP) une équation dont l'inconnue est une fonction $f$ de plusieurs variables et qui fait intervenir les dérivées partielles de $f$ par rapport à ses multiples variables. Cette dénomination est assez tardive. Dans un premier temps, lorsque D'Alembert commence à étudier le problème des cordes vibrantes, il n'y pas de termes pour distinguer les équations aux dérivées partielles des équations différentielles ordinaires (où l'inconnue est une fonction d'une seule variable) : elles sont toutes appelées « équations différentielles ». A partir de 1770, toutefois, une première distinction s'opère, le terme d'« équation aux différences partielles » apparaît sous la plume de Condorcet.

Le problème des cordes vibrantes, tel qu'il est posé au milieu du XVIIIe siècle, consiste à déterminer la fonction $y(t,x)$, qui donne, à chaque instant $t$, l'ordonnée du point d'abscisse $x$ d'une corde fixée en ses deux extrémités. La longueur de la corde est notée $a$ (Figure a ci-dessous).

D'Alembert établit que la fonction $y$ doit vérifier l'EDP $\frac{\partial^2y}{\partial t^2}=\frac{\partial^2y}{\partial x^2}$ en considérant que, sous l'hypothèse de petitesse des vibrations, l'accélération de tout point de la corde est proportionnelle à la courbure de la corde en ce point. Dès 1747, il intègre cette équation aux dérivées partielles et envisage plusieurs types de conditions initiales :

- une corde frappée, c'est-à-dire, initialement à l'état rectiligne d'équilibre et à laquelle on imprime une vitesse initiale,

- une corde pincée, c'est-à-dire tirée de son état d'équilibre et qu'on lâche sans vitesse initiale,

- des situations mixtes avec une position et une vitesse initiales non nulles.

Quel que soit le cas envisagé, il impose la fixité des extrémités comme conditions aux limites.

Dans ses mémoires ultérieurs sur le sujet, D'Alembert s'attarde surtout sur le cas de la corde pincée. Dans ce cas, la fonction $\phi$ qui représente l'allure de la corde à $t=0$ est impaire (symétrique par rapport à l'une des extrémités de la corde) et périodique de période $2a$ (à cause des conditions aux limites). Dans ce cas, la solution est de la forme $y(t,x)=\phi(x+t)+\phi(x-t)$. Pour D'Alembert, toutefois, la fonction ne peut être définie par morceaux. Il refuse, par exemple, de prendre comme condition initiale la fonction $\phi$ représentée par deux morceaux de paraboles accolés (Figure b ci-dessous) :

- $\phi(x)=x(a-x)$ sur l'intervalle $[0,a]$,

- $\phi(x)=x(a+x)$ sur l'intervalle $[-a,0]$,

car l'expression de $\varphi$ change selon l'abscisse considérée. Pour D'Alembert, ce type de situations « surpasse les forces de l'Analyse » et la solution du problème ne s'applique pas dans ce cas. Il en va de même du cas d'une corde formant un triangle à l'instant initial.

Figure a Figure b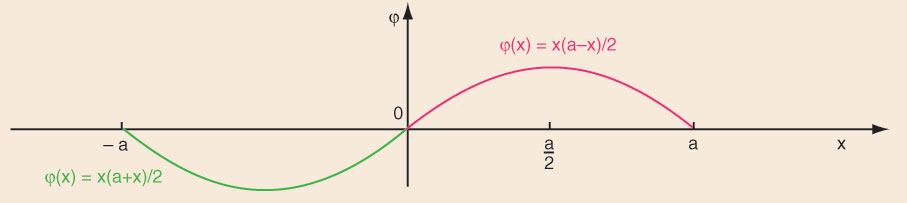

Certains arguments avancés par D'Alembert pour étayer ses restrictions quant à l'applicabilité de sa solution sont fondés. En effet, comme il le signale, dans les deux cas ci-dessus, il est difficile de calculer $\frac{\partial^2y}{\partial x^2}$ en certains points et, à ce titre, l'équation aux dérivées partielles n'est pas vérifiée partout.

Néanmoins, l'approche de D'Alembert dénote un rejet un peu systématique qu'on appelle à l'époque les « fonctions discontinues ». Il changera d'avis sur ce point à la fin de sa vie et ses arguments auront, au passage, contribué à l'élaboration d'une notion plus moderne de continuité.

Retour au sommaire

Retour à l'article