conquete-de-la-precession

Naissance de la Mécanique Céleste

Lorsque Newton disparaît, en 1727, D’Alembert n’a que dix ans. Alors qu’il commence à faire montre de capacités hors normes et de progrès exceptionnels (aux dires de son instituteur l’année suivante, les leçons qu’il recevait ne lui suffisaient plus) l’œuvre révolutionnaire et gigantesque laissée par le savant anglais dans les différents domaines de la science n’a pas encore connu en France le rayonnement qu’elle méritait. On sait que cette oeuvre finira par s’imposer grâce au zèle d’ardents promoteurs comme Voltaire et la marquise du Châtelet (1706-1749). Cette dernière dépensera toute son énergie jusqu’à sa mort à la traduction des fameux Principia, dans lesquels est exposée la célèbre loi selon laquelle deux corps célestes s’attirent proportionnellement à leur masse et inversement proportionnellement au carré de leur distance. On peut voir dans l’énonce de cette loi l’acte fondateur de la branche de l’astronomie que l’on appelle la mécanique céleste, qui comme son nom l’indique a pour objectif d’expliquer et décrire les mouvements des corps célestes. Notons toutefois que la terminologie même de mécanique céleste ne sera mentionnée pour la première fois que beaucoup plus tard, sans doute par Laplace. D’Alembert préfèrera y substituer le concept d’astronomie physique.

Figure 1

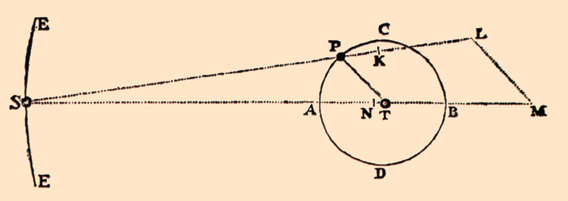Le mouvement des trois corps - Terre T, Soleil S, Lune P - soumis à leurs attractions gravitationnelles mutuelles, tel que Newton la présente dans les Principia. La trajectoire de P autour de T n'obéit qu'approximativement aux deux premières lois de Kepler qui décrivent le mouvement orbital non perturbé. Newton tente de caractériser l'approximation en décomposant l'attraction de S sur P en une force SM dirigée selon ST.

Le problème "des trois corps"

Vers 1745, D’Alembert, accompagné de deux autres illustres mathématiciens Clairaut et Euler, montre un soudain engouement pour un problème spécifique de mécanique céleste, appelé selon une terminologie consacrée qui fera d’ailleurs l’objet d’une entrée dans l’Encyclopédie, le problème des trois corps : lorsque deux corps sont en interaction gravitationnelle selon la loi de l’attraction universelle exposée ci-dessus, leur mouvement l’un par rapport à l’autre aussi bien que par rapport à leur centre de gravité commun s’effectue le long d’une conique, ellipse, parabole ou hyperbole selon l’excentricité. Le positionnement du centre de gravité de chacun des deux corps est alors parfaitement déterminé à tout instant par une formule simple et rigoureuse. Par contre lorsque trois corps de masse donnée sont en interaction gravitationnelle, il en va tout autrement : aucune formule mathématique définie rigoureusement ne permet d’établir la trajectoire de chacun des trois corps ainsi que sa position en fonction du temps. Cependant il est possible, par différentes méthodes analytiques plus ou moins ardues, de construire des développements mathématiques permettant de donner les lois du mouvement des trois corps concernés, avec une précision fixée à l’avance.

La loi de Newton remise en doute

Comme terrain d’application du problème des trois corps, les trois savants sus mentionnés s’attaquent au mouvement orbital de la Lune. En effet, si en première approximation notre satellite décrit une orbite quasi elliptique autour de la Terre, ce mouvement est fortement perturbé par la présence du Soleil et l’attraction que ce dernier exerce. Restait à évaluer les conséquences de cette perturbation. Newton s’était déjà attaqué à ce challenge en 1686, donnant du problème une solution toute synthétique. Malgré quelques travaux de Halley prolongeant cette première tentative, le problème de la détermination théorique du mouvement orbital de la Lune n’avait attiré pratiquement aucun spécialiste jusqu’en 1745.

En juin 1747 et en février – mars 1748, D’Alembert lit devant l’Académie des sciences une série de pièces de mécanique céleste, dont l’une, intitulée Théorie de la Lune, établit les opérations à effectuer pour aboutir à l’élaboration d’une table du mouvement de la Lune. Si dans ses calculs il retrouve de manière relativement fiable les positions observées de notre satellite il bute néanmoins, tout comme Clairaut et Euler, sur un obstacle fondamental, à savoir le mouvement de l’apogée. &A cause de la perturbation solaire, l’apogée de la Lune, à savoir le lieu de son orbite où cette dernière se trouve la plus éloignée de la Terre, n’est pas fixe sur l’orbite, mais se déplace, selon les observations, d’une quantité significative le long de celle-ci., de l’ordre de 40° par an. Or les trois mathématiciens s’accordent pour obtenir indépendamment par la théorie une quantité moitié moindre de cette dernière valeur. De là s’ensuivit bon nombre de conjectures pendant près de deux ans, où nombre d’hypothèses ont été émises pour expliquer la non-conformité entre théorie et observations. Dans une séance publique à l’Académie du 15 novembre 1747, Clairaut ose même remettre en doute la loi d’attraction de Newton en 1/r², envisageant en particulier d’y adjoindre une seconde composante fonction inverse d’une puissance de la distance à trouver. D’Alembert quant à lui est dans un premier temps convaincu que le problème de l’apogée réside dans la manière de poser le problème dynamique, non dans le traitement mathématique à partir de la loi de Newton. Il se fourvoie dans plusieurs hypothèses hasardeuses : la possibilité que l’écart de la Lune à la sphéricité occasionne une force supplémentaire, qu’une force répulsive s’ajoute à la force centrale de Newton, ou l’existence d’un milieu résistant autour de la Terre.

La polémique sur l’ "apogée de la Lune"

Du milieu de 1747 à la fin de 1748, un débat très animé s’installe à propos du problème de l’apogée, entretenu par des échanges épistolaires témoignant de la focalisation sur ce dernier. Euler, qui avait lui-même achevé une Théorie de la Lune (non publiée) en 1745, explique à Clairaut dans une lettre du 3 septembre 1747 comment, pour résoudre le problème, il compte associer à la force de gravitation de Newton un système de tourbillons, hypothèse tout de suite rejetée par Clairaut et que lui-même abandonnera très rapidement. Clairaut se voit quant à lui confronté à des détracteurs l’accusant d’avoir puisé son idée de force supplémentaire dans les travaux d’Euler, ou encore de n’avoir rien apporté de nouveau par rapport aux travaux de Newton. Le célèbre naturaliste Buffon lui-même se mêle au débat. Sans se lancer dans des développements mathématiques, il propose des conjectures, en reprochant à Clairaut, pour des raisons en partie métaphysiques, de remettre en cause la loi de Newton, si simple et belle dans son énoncé et expliquant bon nombre de phénomènes naturels. Au cours de 1748, pendant que Clairaut répond point par point aux suggestions de Buffon, D’Alembert ne cesse de se pencher sur la résolution du problème, en se montrant de plus en plus convaincu que la loi de Newton reste valide, mais il ne semble pas imaginer que le problème de l’apogée pourrait être attribuable à quelque erreur de calcul dans l’application des équations du mouvement de notre satellite. Ce fait apparaît le 17 mai 1749, lorsque Clairaut se rétracte devant l’Académie des sciences, marquant la fin de la « crise » du mouvement de l’apogée. Le savant explique que la prise en compte de termes négligés à tort permet de doubler la vitesse de déplacement de l’apogée et ainsi de rendre compte des observations. Ainsi la cause de tous les débats parfois animés qui ont entouré le problème de l’apogée n’est pas l’imperfection du modèle physique sous-jacent (la force de gravitation) comme cela avait été envisagé par les différents savants, mais uniquement la résolution calculatoire des équations du mouvement. La loi de la gravitation de Newton, si controversée pendant toute la "crise du mouvement de l’apogée" trouvait là encore une occasion de plus de triompher.

Figure 2

Cliquer sur l'image pour l'agrandir

Extrait d'une lettre de D'Alembert à Euler du 20 juillet 1749 sur le problème de l'apogée : "Quoiqu'il en soit, Monsieur, je vous avoüeray, qu'en supposant même que nous ne nous soyons point trompés dans le calcul du mouvement de l'apogée, je ne goute nullement l'opinion où vous paroissés être, et où M. Cairaut etoit aussy, que l'attraction ne suit pas exactement la loy inverse du quarré des distances."

D’Alembert, après quelque période de réflexion où son esprit est préoccupé par d’autres sujets d’investigation, se ralliera finalement rapidement aux solutions de Clairaut. Dans une lettre de septembre 1749 à son ami Gabriel Cramer, il reconnaît la primauté de ce dernier dans la résolution du problème de l’apogée : "Je n’ai point encore examiné l’affaire de l’apogée, il est juste de la laisser à M. Clairaut puisqu’il a eu le bonheur de la trouver le premier, tout ce que je puis vous dire, c’est que l’erreur vient de quelques termes qu’il avait négligés, et qu’on aurait naturellement cru pouvoir l’être puisqu’ils nous ont échappés à tous trois [D’Alembert, Clairaut, Euler]". Dans le même temps, Clairaut dans les Mémoires de l’Académie Royale des Sciences de 1749, rend hommage aux efforts de D’Alembert, tout en ne ménageant pas ses critiques à l’égard de Buffon : "Il était pour moi le seul dont je puisse craindre de blesser les intérêts, puisqu’il était le seul qui se fut véritablement occupé de cette théorie. On ne trouvera pas étonnant que je croie ne devoir donner à Mr. De B. [Buffon] aucune part dans la théorie de la Lune, lors qu’il n’y est que pour quelques réflexions métaphysiques".

Le chef d’oeuvre de la théorie de la précession nutation

Aussitôt le problème réglé, D’Alembert se penche sur un autre sujet de mécanique céleste : l’explication théorique du mouvement de précession et de nutation de la Terre. Récapitulons-en les caractéristiques et l’historique : au II^ème siècle avant J.C, l’astronome grec Hipparque, en comparant latitudes célestes (ou déclinaisons) des étoiles par rapport à l’équateur céleste (prolongement de l’équateur céleste dans l’espace), constate que ces dernières diffèrent de celles données quelques cent cinquante ans auparavant par un autre astronome, Timocharis. Hipparque en conclut que cet effet est dû à un lent déplacement du plan de l’équateur lui-même associé à un déplacement du pôle de rotation de la Terre qui lui est perpendiculaire : c’est le mouvement de précession des équinoxes, appelé ainsi, car la ligne des nœuds, intersection du plan de l’écliptique (orbite de la Terre) et du plan de l’équateur, qui joint donc les deux équinoxes de printemps et d’automne, précesse, autrement dit se déplace dans le plan de l’écliptique, selon un cycle d’environ 26 000 ans. En conséquence, dans le même temps, l’axe de rotation de la Terre, tel celui d’une toupie, décrit un cône dans l’espace, centré sur l’axe de l’écliptique (perpendiculaire au plan orbital de la Terre autour du Soleil).

Or, à ce mouvement général connu depuis l’antiquité viennent s’ajouter de petites oscillations que l’on appelle la nutation. La plus grande oscillation, encore appelée nutation principale, est une boucle de 10’’ d’amplitude parcourue en 18,6 ans. Il faudra attendre le XVIII^ème siècle pour que celle-ci soit mise en évidence par l’observation, grâce à un astronome anglais, James Bradley (1693-1762). A partir de 1725, ce dernier observe régulièrement, à l’aide d’un instrument appelé secteur, certaines étoiles dont  de la constellation du Dragon, qui a l’avantage de passer à la verticale du site d’observation, donc d’offrir des relevés d’autant plus précis. Très rapidement, il constate que les passages d’étoiles au méridien ne s’effectuent pas à une même distance zénithale. De petites modifications surviennent, de l’ordre de quelques secondes d’arc, et selon un cycle annuel : Bradley vient de révéler le phénomène d’aberration de la lumière, dû au déplacement de la Terre sur son orbite, dont il annoncera la découverte à la Royal Society, en forme de lettre à Halley, en janvier 1729. Fort de ce coup d’éclat, l’astronome anglais continue ses observations au secteur et met en exergue, au bout d’une vingtaine d’années, un autre phénomène, à savoir une boucle parcourue par chaque étoile, qui est la conséquence même de la boucle parcourue par le pôle de rotation de la Terre dans l’espace. L’astronome vient en fait de découvrir la nutation, qu’il annoncera officiellement dans un mémoire daté du 31 décembre 1747.

Il restait à expliquer ce nouveau phénomène par la théorie. Il est fort probable que la découverte retentissante de la nutation va servir de catalyseur à D’Alembert pour s’atteler à cette lourde tâche. En effet, dès la fin de 1748, il semble avoir déjà largement entamé ses calculs dans cette perspective. Dans une lettre du 5 décembre 1748 à Gabriel Cramer, il explique "J’ai composé là-dessus un grand mémoire qui sera imprimé avec beaucoup d’autres recherches sur le système du monde dans le courant de l’année prochaine". Sa diligence sera à la mesure de sa motivation puisque dès juillet 1749, l’ouvrage paraît sous forme d’un traité que l’on peut considérer à juste titre comme un chef d’œuvre.

Figure 3

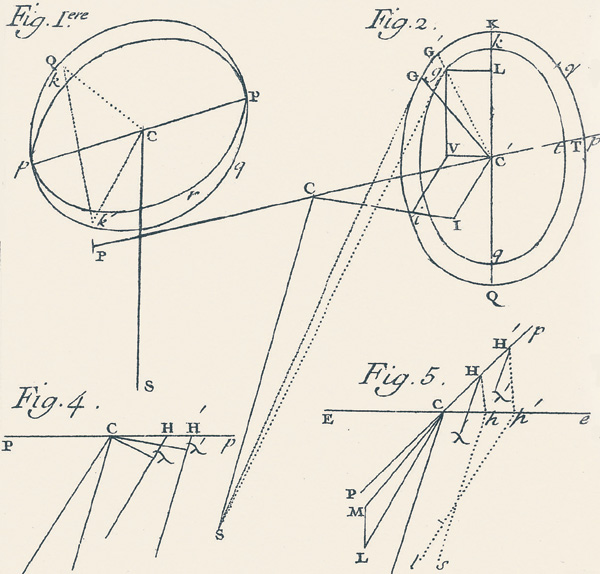Figures de support au Traité de la précession (1749) : sur la figure 2, D'Alembert découpe le bourrelet équatorial de la Terre par tranches autour de l'axe des pôles PP' (une tranche est représentée ici) et calcule la perturbation due à l'attraction lunisolaire sur chaque tranche. Il aboutit ainsi aux équations du mouvement de l'axe de rotation de la Terre.

La précession et la nutation de la terre s’expliquent par un même phénomène, l’influence conjuguée de la Lune et du Soleil sur le bourrelet équatorial de la Terre : le couple gravitationnel exercé par ces deux corps célestes sur le bourrelet s’accompagne d’un mouvement de balancement de l’équateur et donc déplace l’axe des pôles qui lui est perpendiculaire, dans l’espace. On doit à Newton, dans son Livre I des Principia, d’avoir bel et bien expliqué le premier l’origine gravitationnelle de la précession. Mais pour en donner une valeur conforme à celle mesurée (les équinoxes se meuvent de 50’’ par an sur l’écliptique, soit un tour complet en à peu près 26 000 ans) il n’avait pas hésité à effectuer un certains nombre de simplifications et d’erreurs, afin sans doute de s’affranchir de certaines difficultés calculatoires inhérentes au développement insuffisant des mathématiques de l’époque. Par exemple il remplace le bourrelet équatorial de la Terre par un anneau solide "composé de petites lunes", ce qui rend la suite de ses calculs hasardeuse.

D’Alembert, dans l’introduction de son fameux Traité de la précession de 1749, n’hésite pas à effectuer un compte-rendu circonstancié de toutes ces insuffisances, insistant sur la nécessité de construire une nouvelle méthode, qu’il développe dans la suite de l’ouvrage. Pour déterminer le mouvement de l’axe des pôles de la Terre, il utilise le fameux principe éponyme présenté dans son Traité de Dynamique de 1743, selon lequel "pour trouver à chaque instant le mouvement d’un corps animé par un nombre quelconque de forces, il faut regarder le mouvement qu’il avait dans l’instant précédent". Puis l’auteur calcule le couple perturbateur lunisolaire sur tout le bourrelet équatorial. Pour cela il fait appel au calcul intégral, précieux outil mathématique qu’il a lui-même contribué à développer. Rapidement, il obtient les équations du mouvement du pôle de la terre dans l’espace, et peut ainsi d’une part retrouver, en la quantifiant, la précession des équinoxes, d’autre part prouver et déterminer en détail le mouvement de nutation, découvert deux ans auparavant. En particulier il explique par les lois de la mécanique, pourquoi la période de ce mouvement coïncide exactement avec celle du mouvement des nœuds de la Lune (intersections entre le plan de l’écliptique et le plan de l’orbite lunaire). De nouveaux concepts apparaissent dans le Traité de la précession de D’Alembert, comme celui d’ "axe instantané de rotation", autrement dit le lieu de tous les points d’un solide en rotation dont la vitesse est nulle par rapport au barycentre. De plus, en comparant l’amplitude de la boucle de nutation principale (de l’ordre de 9 secondes d’arc) due à la seule influence gravitationnelle de la Lune, avec la quantité de précession (de l’ordre de 50 secondes par an) due à l’action combinée de la Lune et du Soleil (la première pour deux tiers, le second pour un tiers), D’Alembert en déduit que le rapport de la masse de la Terre à celle de la Lune est voisin de 80, résultat remarquablement proche de la valeur actuelle de 81,3, alors que la valeur de 40 communément admise à l’époque, provenait de la théorie de Newton. Deux facteurs ont contribué indiscutablement à cette amélioration éclatante : la rigueur et la qualité de la théorie de D’Alembert d’une part, la précision des observations de Bradley d’autre part.

La querelle de priorité avec Euler

Le Traité de la précession fera l’objet d’une controverse parmi d’autres entre D’Alembert et Euler, dont les relations s’étaient déjà fort détériorées à la suite du rôle joué par ce dernier dans le report du prix de 1750 de l’Académie de Berlin sur la résistance des fluides, qui aurait dû logiquement revenir à D’Alembert (voir par ailleurs). En effet, le 5 mars 1750, Euler lit devant l’Académie de Berlin un mémoire intitulé "Recherches sur la précession des équinoxes et sur la nutation de l’axe de la Terre" : curieusement le titre est le même que celui du traité de D’Alembert, mais l’analogie ne s’arrête pas là. En lisant le texte imprimé, D’Alembert constate d’une part que la méthode utilisée par Euler, qui ne s’accompagne d’ailleurs pas d’une véritable démonstration, est très proche de la sienne, d’autre part que son propre nom n’est jamais cité, alors qu’il estime à juste titre avoir été le premier à donner l’explication du phénomène de nutation.

Afin de mieux clarifier sa revendication de priorité, D’Alembert envoie à l’Académie de Berlin un mémoire, daté de juin 1752, dans lequel il cite trois lettres d’Euler montrant clairement que ce dernier avait explicitement reconnu les travaux antérieurs de D’Alembert. Dans l’une d’entre elles, du 7 mars 1750, Euler précise "[…] depuis que j’ai réussi mieux dans la recherche de ce même sujet [la précession], ayant été soutenu par quelques lumières de votre ouvrage dont je me suis éclairci peu à peu, j’ai été en état de mieux juger de vos excellentes conclusions ». Dans une autre, du 29 juin 1751, il précise que l’astronomie était redevable au savant français de l’explication de la nutation de l’axe de la Terre". Enfin, pour "enfoncer le clou", D’Alembert, au sein du même mémoire, se lance dans une comparaison approfondie et minutieuse du travail d’Euler, montrant comment il ressemble point par point, tables de correspondance à l’appui, à son propre traité. L’allusion à un plagiat est sans équivoque. La controverse trouvera un épilogue grâce à un véritable mea culpa de la part d’Euler dans un "Avertissement au sujet des recherches sur la précession des équinoxes" publié dans l’Histoire de l’Académie de Berlin (1752), dont la teneur vaut d’être mentionnée : "Quoique ce mémoire soit inséré dans le volume des Mémoires de l’Académie pour l’année 1749, l’auteur déclare, qu’il ne l’a composé qu’après avoir lu l’excellent ouvrage de M. D’Alembert sur cette matière ; et qu’il ne fait pas la moindre prétention à la gloire, qui est due à celui qui a le premier résolu cette importante question. Comme il s’est borné à exposer uniquement la route, qu’il a suivie pour développer ce problème, il n’y a ajouté aucun discours préliminaire dans lequel il n’aurait pas manqué d’indiquer que c’est uniquement à M. D’Alembert, qu’on est redevable de la discussion de cette importante matière. D’ailleurs l’ouvrage de M. D’Alembert fut reçu d’abord avec un applaudissement si général, qu’il a paru superflu alors d’informer le public d’un fait aussi bien constaté et reconnu de tout le monde. Mais puisque les circonstances pourraient tomber dans l’oubli avec le temps, on a jugé nécessaire d’en instruire le public par cet avertissement".

D’Alembert astronome

Si le Traité de la précession marque un succès retentissant de D’Alembert dans le domaine de l’astronomie, son intérêt pour cette science ne se démentira jamais par la suite. Au tournant des années 1750, d’autres sujets, sont abordés de manière récurrente dans ses Opuscules ou ses Recherches sur Différents points du Système du Monde, comme les comètes, les mouvements de Saturne et Jupiter, mais aussi la Figure de la Terre qui occupera une place de choix dans ses investigations de physique mathématique. Depuis que les missions astro-géodésiques des Académiciens en Laponie et au Pérou vers 1735 ont conclu à la validité de la théorie de Newton selon laquelle la Terre est aplatie aux pôles et renflée à l’équateur, les savants de l’époque se sont efforcés de répondre à un certain nombre de questions : quelle est le contour exact d’un méridien terrestre ? Répond-il à une figure géométrique simple ? Cette figure varie-t-elle avec la longitude ? Comment la déduit-on des relevés astronomiques des hauteurs d’étoiles effectués en différents points du globe ? Peut-on déduire certaines de ces informations de l’observation minutieuse de la Lune effectués en des lieux distants (par l’effet de parallaxe) ? Tout en essayant de répondre à toutes ces questions, D’Alembert montrera une grande indifférence quant aux résultats d’observations effectués à son époque, même si de temps en temps il est obligé d’y avoir recours, comme part exemple la découverte de la nutation par Bradley ou les tables du mouvement de la Lune de Le Monnier. Car seuls l’attireront le traitement purement mathématique et la recherche de méthodes totalement affranchies des contingences de l’astronomie d’observation. Une phrase dans le Tome IV de l’Histoire des Mathématiques de Montucla résume bien cet état d’esprit. "Celui-ci [D’Alembert] n’avait pas la patience de suivre de longs calculs appliqués à l’observation ; il ne voulait que des formules élégantes, à peine les avaient-il évaluées, qu’il croyait tout fini".

On ne peut placer sous silence les polémiques sur des sujets d’astronomie qui verront le jour de nouveau entre Clairaut et D’Alembert, par journaux interposés, comme le "Mercure", le "Journal des Savants" ou le "Journal Encyclopédique". Elles concernent dans un premier temps les tables de la Lune, que les deux savants s’évertueront, entre 1754 et 1762, à peaufiner par la théorie pour les rendre plus conformes aux observations. Puis viendra le fameux épisode du passage de la comète de Halley en 1759, après ceux de 1531, 1607 et 1682, dont Clairaut et Lalande vont calculer la trajectoire et le retour avec une précision (de l’ordre de un mois) bien supérieure à celle des travaux antérieurs, en tenant compte de l’influence perturbatrice de Jupiter et Saturne. D’Alembert contestera avec beaucoup de vigueur (et sans doute sans véritable justification) la validité de la méthode de son concurrent.

Figure 4

Jérôme Lalande (1732-1807) est l'un des astronomes les plus entreprenants et le plus prolixes du siècle des Lumières. Plus calculateur que théoricien, il regarde avec une certaine distance les travaux de mécanique céleste de D'Alemnbert, lequel le considère comme un "petit drôle". Dans l'Encyclopédie méthodique, Mathématiques, au cours de l'année 1780, Lalande reprend presque "à zéro" tous les articles d'astronomie que D'Alembert avait publiés dans l'Encyclopédie. Voir Encart 2.

Enfin D’Alembert se penchera dans différents ouvrages sur le thème récurrent sur l’attraction des sphéroïdes (solides voisins d’une sphère), en établissant les lois d’équilibre d’un sphéroïde en rotation. Il envisage le premier le cas où l’intérieur d’un sphéroïde n’est pas homogène, mais est constitué de couches de densités différentes, puis il dresse les équations donnant la forme du sphéroïde. Il montre que dans le cas où on considère l’intérieur de la Terre sous forme d’un fluide homogène, cette dernière peut se trouver dans deux états d’équilibre, avec un rapport d’aplatissement respectivement de 1/230 et de 1/681.

Notons que D’Alembert sera le rédacteur exclusif de tous les articles de l’Encyclopédie concernant l’astronomie, ce qui confirme sa connaissance globale de cette science. Si son délaissement marqué pour les observations en tant que telles ne permettent pas de le ranger dans la famille des astronomes traditionnels, comme le furent au XVIII^ème siècle LeMonnier, Clairaut ou Lalande, ses succès dans l’élaboration et le perfectionnement des théories dynamiques des corps célestes font de lui un des grands précurseurs de la Mécanique Céleste, qui est une des branches à part entière de l’astronomie moderne.

Bibliographie

Euler, Leonhard, "Recherches sur la précession des équinoxes et sur la nutation de l'axe de la Terre", Histoire de l'Académie de Berlin, année 1749 (1751), p.239-325

Montucla, Jean-Etienne, Histoire des Mathémaques, tomes III et IV achevés et publiés par J. de Lalande, Paris, H. Agasse, 1892

Newton, Isaac, Principes Mathématiques de la Philosophie Naturelle, Trad. Française Mme du Châtelet, 2 vol., Paris, Desaint & Saillant et Lambert, 1759, réimpression J.Gabay, 1990

D'Alembert, Jean Le Rond, "Précession & Nutation (1749-1752)", Oeuvres Complètes, Vol. I.7, Dir. Michelle Chapront-Touzé & Jean Souchay, CNRS Editions

D'Alembert, Jean Le Rond, "Premiers Textes de Mécanique Céleste (1747-1749)",Oeuvres Complètes, Vol.I.6, Dir. Michelle Chapront-Touzé, CNRS Editions

D'Alembert: Mathématiciens des Lumières

À la conquête de la précession