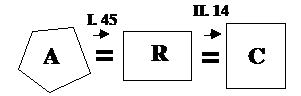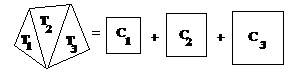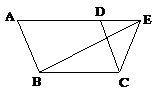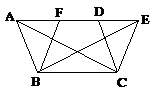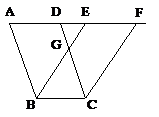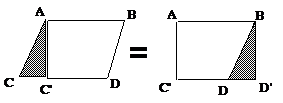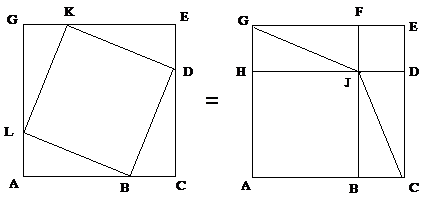Eudème de Rhodes affirme que
l'égalité de deux triangles ayant un côté
égal à un côté et deux angles égaux
à deux angles, chacun à chacun — c'est l'objet
de la Proposition I. 26 des Éléments d'Euclide
— était déjà connue de Thalès de
Milet. Car nécessairement, dit-il, celui-ci devait en faire
usage dans la méthode qu'il avait mise au point pour
déterminer, du rivage, l'éloignement d'un bateau qui s'en
approche. Ce témoignage, transmis par Proclus, nous apprend deux
choses.
• Eudème — comme beaucoup
d'historiens modernes — procédait par reconstruction
rationnelle : si Thalès avait inventé une certaine
méthode, il devait avoir aussi reconnu tous les résultats
géométriques qu'elle présuppose.
L'inférence est évidemment très incertaine.
• La tradition (pseudo) historique
considérait que l'intérêt de la recherche
géométrique résidait dans la possibilité de
déterminer la position et l'éloignement de points non
accessibles à la mesure directe. L'anecdote de la mesure de la
hauteur de la Grande Pyramide procédait du même esprit
(voir chapitre 1).
Arpentage et géométrie
Hérodote, on s'en souvient, avait
suggéré que la géométrie tirait son origine
de l'arpentage égyptien, autrement dit de la mesure des
surfaces. Mais en fait, les arpenteurs utilisaient des
procédures parfois sommaires et approximatives quoique simples
à mettre en œuvre. Ainsi, pour évaluer l'aire d'un
quadrilatère quelconque ABCD — plutôt que de le
diviser en deux triangles à évaluer — ils se
contentaient d'en mesurer les côtés, de faire les demies
sommes des côtés opposés,
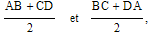
et de les multiplier l'une l'autre (voir figure 1
et 2 ci-dessous). La procédure est d'autant plus
approchée que la forme de ABCD est éloignée de
celle d'un rectangle.
Figure 1 - Ostrakon d'arpentage (fin du I er siècle avant notre ère)
Il s'agit d'une liste de
mesures d'aires pour des champs quadrangulaires du pays de Kalliedon,
mis en culture par Petechonsis, aires toutes calculées selon la
formule de la figure 1 et éventuellement arrondies (par
excès cela va de soi) pour éviter les fractions les plus
petites produites par multiplication. Les quatre dimensions sont
présentées sous la forme
.
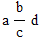L'unité de mesure
linéaire est le schöne (environ 50 m); celle de surface,
l'aroure (schöne au carré, soit environ 1/4 d'hectare). Ces
relevés servaient à calculer l'impôt sur la base
d'un calcul de surface toujours majoré !
Figure 2
Pour exprimer l'aire de ABCD on prend :
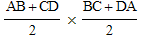
Ce qui revient à l'assimiler à un rectangle EFGH vérifiant :
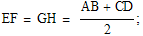
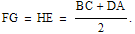
Cela dit, il y avait moyen de combiner les deux
approches en montrant qu'une des tâches de la
géodésie (ou géométrie appliquée)
est précisément de mesurer indirectement certaines
grandeurs : profondeur d'un canal, hauteur d'une montagne,
éloignement entre l'observateur et un point inaccessible
… C'est ce point de vue que Héron d'Alexandrie
développera de manière systématique, au I er
siècle de notre ère, dans son traité de la Dioptre. La
progression de son exposé évoque irrésistiblement
celle d'Euclide : explication de procédures
élémentaires ensuite combinées pour
résoudre des questions complexes. Outre la manipulation
d'instruments (la dioptre bien sûr et différentes sortes
de règles), il y est constamment fait usage de la
proportionnalité des côtés entre triangles
semblables, propriété qui, dans l'enseignement
élémentaire français actuel, est très
significativement appelé « théorème de
Thalès ».
Héron n'était pas un simple
arpenteur, mais aussi un fin lettré. Ainsi, dans sa section XXV
il pose le problème suivant : « Les bornes d'un terrain
étant devenues invisibles sauf deux ou trois, retrouver à
l'aide du plan existant les autres bornes ». Par ailleurs une
bonne partie du traité est consacrée à une
série de questions dont le but est d'amener l'eau d'un point B
à un point A, au besoin en creusant un canal à travers
une montagne, en ligne droite, à partir des deux entrées
données, ainsi que des bouches d'aération. Dans l'un et
l'autre cas, il s'agit incontestablement de clins d'œil à
Hérodote, d'une part à son hypothèse concernant
l'origine de la géométrie (voir chapitre 1),
d'autre part à la mention que l'historien fait d'une très
belle réalisation technique de l'époque archaïque,
le tunnel d'Eupalinos de Mégare, creusé dans l'île
de Samos, vers 530 avant notre ère. Destiné à
approvisionner la cité en eau, ce souterrain est long d'un bon
kilomètre. Le creusement a été entrepris
simultanément par deux équipes, de part et d'autre de la
montagne !
Figure 3 - Tunnel d'Eupalinos
Selon Hérodote, la
cité de Samos avait réalisé les trois plus
importants ouvrages architecturaux que possédait la Grèce
(à son époque) : un môle pour abriter le port, le
grand temple d'Héra et le tunnel d'Eupalinos. Le creusement,
entrepris des deux côtés de la montagne, présuppose
un certaine habileté géodésique pour maintenir un
alignement des deux percées et une pente à peu
près continue pour faciliter l'écoulement de l'eau. On a
voulu y voir l'influence de Pythagore, natif de Samos. Mais d'une part
celui-ci quitta sa cité pour fuir la tyrannie de Polycrate,
d'autre part l'architecte Eupalinos était de Mégare et
non de Samos. De plus, grâce à Héron qui
décrit les procédures à suivre, on voit que les
connaissances géométriques mobilisées sont
minimales.
Que les ingénieurs, mécaniciens ou
architectes rendent compte de leurs pratiques en montrant comment
celles-ci s'appuient sur certains résultats de la
géométrie théorique se comprend bien. C'est le
moyen d'accroître leur prestige, de faire reconnaître
à la fois l'utilité et la technicité de leurs
savoirs. A l'inverse, les géomètres se sont-ils
souciés des possibilités d'application de leurs
résultats? Nous avons déjà vu qu'ils optent pour
des formulations abstraites : plutôt que de mesure d'une aire,
ils parlent de "quadrature". Mais un rapide survol du premier Livre des
Éléments montre qu'Euclide a voulu
établir un lien constitutif entre la quadrature des aires
rectilignes et la démarche axiomatico-déductive.
Figure 4
Géomètres et arpenteurs en discussion (à gauche)
Portrait d'un géomètre (probablement Euclide) dans un manuscrit d'arpentage romain (à droite)
Les arpenteurs romains
(on les appelle "agrimenseurs") constituaient une corporation
réglementée et reconnue. Ils comprirent qu'ils pouvaient
augmenter leur prestige social en se présentant comme les
interlocuteurs des géomètres (1) ou en se plaçant
sous le patronage d'Euclide (2) comme on le voit dans les illustrations
de ces manuscrits d'arpentage. Plusieurs de leurs traités,
davantage par coquetterie que par utilité, citent des
résultats de géométrie théorique.
De la quadrature des aires rectilignes au théorème de l'hypoténuse
Dans la Proposition II. 14, l'Auteur des Éléments
résout le problème de la quadrature des aires rectilignes
: « Construire un carré égal à une figure
rectiligne donnée ». Pour ce faire il procède en
deux temps : il suppose avoir trouvé un rectangle, R,
égal à la figure A — il a expliqué comment
faire dans la Proposition 45 du Livre I — puis il démontre
comment trouver un carré C, équivalent en aire au
rectangle R (voir figure 5 ci-dessous).
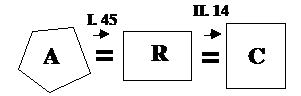
Figure 5
Grâce à la Proposition I.
45 la quadrature des figures rectilignes quelconques est ramenée
à un cas particulier : celle des rectangles.
On peut envisager les choses autrement. Clairement
toute figure rectiligne peut être découpée en
triangles : un pentagone P est composé (d'au moins) trois
triangles (voir figure 6 ci-dessous).
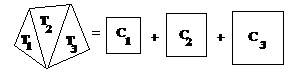
Figure 6
Supposons que nous sachions trouver un
carré équivalent en aire pour n'importe quel triangle.
Pour résoudre le problème de la quadrature des aires
rectilignes, il suffira de savoir comme on peut trouver un carré
équivalent à la somme de deux (trois, quatre,
cinq …) autres carrés.
Bien entendu, par associativité, il suffit
de savoir le faire pour deux carrés. Car si, par exemple, nous
divisons notre pentagone P en trois triangles T 1, T 2, T 3, que nous
supposions avoir trouver des carrés équivalents C 1, C 2,
C 3, nous prendrons d'abord la somme des deux carrés C 1 et C 2,
sous forme d'un carré, C 12, puis la somme des deux
carrés C 12 et C 3. Il faut donc que nous nous posions le
problème suivant : « comment trouver un carré
équivalent à la somme de deux carrés
donnés ? ».
La réponse se trouve dans l'une des plus
célèbres Propositions d'Euclide, l'avant dernière
(47e) de son premier Livre, le théorème dit de
l'hypoténuse :
Dans les triangles rectangles, le carré sur le
côté sous-tendant l'angle droit est égal aux
carrés sur les côtés contenant l'angle droit.
Il établit aussi la converse dans le
théorème qui suit. La propriété des
carrés décrits sur les côtes d'un triangle
énoncée ici est donc caractéristique de
l'espèce "rectangle". D'un point de vue pratique, cette converse
n'est pas sans intérêt. Comme le dit l'architecte romain
Vitruve, en prenant trois règles de 3, 4, et 5 pieds, on
construira une équerre très exacte, découverte
fort utile, ajoute-t-il, pour la construction des degrés d'un
escalier. La détermination de tels triplets de nombres (a, b,
c), vérifiant a 2 + b 2 = c 2, était déjà
connue des calculateurs babyloniens.
Figure 7 - Tablette cunéiforme Plimpton 322
[Cliquer sur l'image pour l'agrandir]
Cette tablette, qui date
du 2e millénaire avant J.C. (au plus tard vers 1600) comporte
trois colonnes de nombres en notation sexagésimale et une
numérotation des entrées de 1 à 15. Trois nombres
entiers (a, b, c) constituent un triplet pythagoricien s'ils
vérifient (P) : a ² + b² = c² . Les triplets enregistrés sur la tablette sont de la forme : [(b/a)² , b, c] avec (a, b, c ) vérifiant (P).
Pourquoir avoir réalisé une telle table?
Témoigne-t-elle d'une connaissance du théorème de
l'hypoténuse (c'est-à-dire une interprétation
géométrique)? Plusieurs documents le font penser (voir
par exemple la tablette YBC 7289
contenant la valeur approchée de la diagonale d'un
carré). Une certitude demeure : les techniques
mathématiques des savants babyloniens, bien avant celles des
Grecs, n'étaient pas cantonnées à de simples
applications pratiques.
Eudème, on s'en souvient, avait
tenté de déterminer les théorèmes
géométriques que Thalès, selon lui, ne pouvait
ignorer. D'autres auteurs, plus récents semble-t-il, firent de
même pour Pythagore et plusieurs auteurs tardifs (outre Vitruve,
Plutarque, Athénée de Naucratis, Diogène
Laërce, Porphyre …) lui attribue la découverte du
théorème qui, aujourd'hui encore, porte son nom. La chose
les intéressa car, depuis un certain Apollodore le calculateur
(II e s. avant J. C.), on associait la prétendue
découverte de Pythagore à un sacrifice carné,
pratique interdite par les préceptes de la secte
pythagoricienne. Les sources classiques (Hérodote, Isocrate,
Platon, Aristote …) mentionnent en effet Pythagore comme
l'inventeur d'un « genre de vie » fondé sur de
multiples prescriptions religieuses et observances rituelles, la
croyance à la transmigration des âmes, le refus de
certains cultes civiques mais aussi la volonté d'influencer le
régime politique de certaines cités de
Grande-Grèce (Italie du Sud, Sicile) … Rien n'indique
qu'il se consacra à la géométrie. Même
Proclus ne cache pas son scepticisme. Il préfère insister
sur la perfection de la preuve euclidienne. Suivons son exemple.
La démonstration euclidienne du théorème de l'hypoténuse
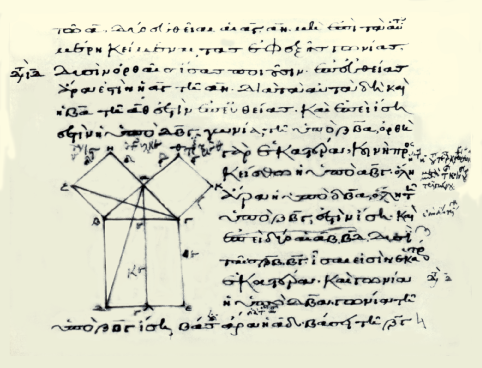
Figure 8 - Euclide, Éléments, Livre I, Proposition 47
.
Soit le triangle rectangle ABC ayant l'angle sous BAC droit.
Je dis que le carré sur BC est égal aux carrés sur BA, AC.
En effet d'une part que le
carré BDEC soit décrit sur BC, d'autre part les
carrés GB, HC sur BA, AC; et que par le point A, soit
menée AL, parallèle à l'une quelconque des BD, CE.
Et que AD, FC soient jointes.
Le style euclidien possède certaines
caractéristiques que nous avons déjà
rencontrées dans les fragments d'Hippocrate : exposé
synthétique, forme déductive, combinaison d'un texte et
d'un diagramme pourvu de lettres, indissociablement liés l'un
à l'autre et indispensables à la réalisation de la
preuve. Les lettres sont les seules parties du discours
mathématique qui n'appartiennent pas à la langue
naturelle. Euclide n'utilise pas de symboles et son discours ne fait
appel qu'à une toute petite portion de la langue grecque,
grâce à l'usage de phrases
stéréotypées quasi-formulaires. Il désigne
les figures d'une manière économique. Par exemple il
parle du carré BDEC (voir figure 8 ci-dessus) car tous ces
sommets sont mentionnés dans le texte, mais il désigne
les carrés sur AB, AC seulement par deux sommets opposés,
respectivement (B, G) et (H, C) car cela lui suffit.
Le nœud de la démonstration consiste
à établir que le rectangle BL et le carré ABFG
sont égaux car ces quadrilatères sont doubles de
triangles égaux, respectivement ABD et FBC. Euclide
établit l'égalité préalable de ABD, FBC
grâce à un cas d'égalité des triangles (I.
4) : nos deux triangles ont deux côtés égaux
à deux côtés, lesquels contiennent des angles
égaux.
vvvvvv
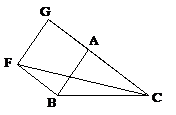
Figure 9
Auparavant Euclide a soigneusement
prouvé l'égalité des angles ABD, FBC comme sommes
de deux angles égaux, deux à deux.
D'un point de vue moderne, l'égalité des
triangles découle de ce qu'ils se déduisent l'un de
l'autre par rotation de 90°.
La suite est simple : de la même
manière, le rectangle CL sera égal au carré ACKH
(Euclide se dispense des détails). Mais la réunion des
rectangles BL et CL constitue le grand carré BDEC, donc celui-ci
est égal aux deux carrés BG (+) HC.
Mais comment justifier le fait que le rectangle
BL (resp. le carré BG) est double du triangle ABD (resp. FBC)?
Ceci est établi dans un théorème antérieur
dont le cadre, plus général, combine triangles et parallélogrammes : la Proposition I. 41. Elle se présente ainsi :
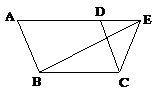
Figure 10
On a un parallélogramme ABCD et
un triangle, BCE, qui ont donc la même base, BC. On suppose, en
outre, qu'ils sont situés dans les mêmes
parallèles, les droites BC, AE. On veut montrer que ABCD est le
double du triangle BCE.
Avant d'aller plus avant dans la preuve de I. 41
il nous faut vérifier que celle-ci s'applique bel et bien dans
I. 47, par exemple pour notre carré BG et le triangle FBC (Voir
figure 8). Deux points sont évidents : un carré
(comme BG) est un parallélogramme, c'est-à-dire
une figure «à lignes parallèles». Idem pour
un rectangle comme BL. En outre FBC et BG ont bien la même base,
BF. Reste à vérifier qu'ils sont bien dans les
mêmes parallèles.
Les droites FB, GA sont en effet
parallèles (puisque BFGA est un carré par construction).
Il faut donc montrer que le sommet C est bien sur le prolongement de la
droite GA. Car on pourrait imaginer que les droites GA, AC constituent
une ligne brisée (en A) : il n'en est rien. Euclide remarque :
« Puisque chacun des angles sous BAC, BAG est droit, alors
relativement à une certaine droite : BA, et en un point A
qui est sur elle, les deux droites AC, AG, non placées du
même côté, font des angles adjacents égaux
à deux droits. Donc CA est en alignement avec AG. Alors pour la
même raison BA est aussi en alignement avec AH ». Autrement
dit, il se réfère à sa Proposition I. 14. Bon
nombre des premiers résultats du Livre I consistent
précisément à justifier ce qu'un lecteur trop
pressé pourrait considérer comme totalement
évident, par exemple un alignement.
Plus rien désormais ne s'oppose à
ce que nous utilisions le résultat contenu dans I. 41 pour
établir le théorème de l'hypoténuse.
Grâce à I. 47 nous saurons trouver la "somme" de deux
carrés donnés sous forme d'un carré. En effet, si
les côtés des carrés donnés sont pris comme
deux segments, AB, AC, nous formerons un triangle rectangle dont les
côtés de l'angle droit sont égaux à AB, AC.
Alors l'hypoténuse sera le côté du carré
"somme". Si on voulait faire leur différence, on prendrait le
plus grand comme hypoténuse d'un (autre) triangle rectangle, le
plus petit comme l'un des côtés de l'angle droit. Le
côté restant sera le côté du carré
équivalent à la différence des deux carrés
donnés.
Revenons à la preuve de I. 41. Euclide
joint la diagonale AC (voir Figure 6). Il construit ainsi le triangle
ABC qui, lui aussi, a BC pour base et est situé dans les
mêmes parallèles. Ceci fait, il énonce deux
assertions qui entraînent immédiatement le résultat
cherché :
(a) Les triangles ABC, EBC,
parce qu'ils ont la même base et sont dans les mêmes
parallèles, sont égaux entre eux.
(b) Le triangle ABC est la
moitié du parallélogramme ABCD, parce que AC est la
diagonale et que la diagonale d'un parallélogramme le coupe en
deux parties égales.
Cette seconde propriété est assez simple et
découle de l'égalité des triangles ABC, ADC. Elle
a une conséquence intéressante. Complétons la
figure ci-dessus en introduisant le point F tel que EF = BC (figure 11
ci-dessous).
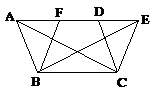
Figure 11
BCEF est un parallélogramme, lui aussi sur la
même base et dans les mêmes parallèles et BE en sera
la diagonale.
D'après (b), le triangle EBC sera donc la moitié du parallélogramme BCEF.
Autrement dit, grâce à la dichotomie du parallélogramme par la diagonale (b), si l'affirmation (a) est vraie, l'assertion (c) :
«Les parallélogrammes qui ont la
même base et qui sont dans les mêmes parallèles sont
égaux entre eux»,
le sera également et réciproquement. De manière synthétique :
«les parallélogrammes ou triangles qui
ont la même base et qui sont dans les mêmes
parallèles sont égaux entre eux».
Euclide traite les cas "triangles" (a) et "parallélogrammes" (c) séparément, dans I. 37 et I. 35 respectivement. Quant à (b),
il l'est dans I. 34. Pour résumer le cheminement logique suivi
dans cette portion du Livre I, on peut dire que les
théorèmes I. 34-35 sont donc les fondements de la
théorie de l'équivalence en aire contenue, notamment,
dans les propositions I. 37, 41, 42, 47 et II. 14. A partir de
là, il est facile de généraliser dans deux
directions :
• si des parallélogrammes ou triangles ont des bases égales (et plus seulement la même base) et s'ils sont dans les mêmes parallèles, ils sont égaux entre eux.
• si des parallélogrammes ou triangles ont des bases inégales
et s'ils sont dans les mêmes parallèles, ils seront
inégaux et le plus grand sera celui qui a la plus grande base.
La première généralisation
est faite dans les Propositions I. 36-38; la seconde est
présupposée dans la Proposition VI. 1 : « les
parallélogrammes ou triangles qui sont dans les mêmes
parallèles sont entre eux comme leurs bases » laquelle,
à son tour, est l'élément de base de toute la
théorie des proportions entre figures semblables, exposée
dans les Livres VI (figures planes) et XI (solides). Cela confirme, si
besoin était, le caractère élémentaire de
I. 35, pierre de fondation du dernier tiers du Livre I. Sa preuve
mérite donc qu'on s'y arrête.
La preuve de la Proposition I. 35
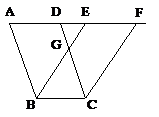
Figure 12
Soient ABCD, EBCF des parallélogrammes sur la même base BC, et dans les mêmes parallèles AF, BC.
Je dis que le parallélogramme ABCD est égal au parallélogramme EBCF.
On peut distinguer différents éléments dans
cette démonstration. Plusieurs résultats
antérieurs sont utilisés :
• I. 33, puisque ABCD et EBCF sont des parallélogrammes, on a : AD = BC et BC = EF;
• I. 29, pour établir l'égalité des
angles FDC, EAB, parce que les droites AB, CD sont parallèles.
• I. 4 (cas d'égalité des triangles), pour montrer que les triangles EAB, DFC sont égaux.
Nous pourrions donc
poursuivre notre parcours régressif en recherchant les
éléments mobilisés dans ces Propositions. Sans
entrer dans les détails, contentons-nous d'une remarque à
propos de la Proposition I. 29. Celle-ci affirme que « si une
ligne droite tombe sur des droites parallèles, elle fait (i) des angles alternes égaux entre eux, et aussi (ii) l'angle extérieur égal à l'angle intérieur et opposé, et (iii) les angles intérieurs et du même côté égaux à deux droits ». C'est 29(ii) qui est utilisée ici pour établir une égalité angulaire, 29(i)
l'est dans I. 34 pour le même genre d'inférence. Cette
Proposition I. 29 est en fait quasiment équivalente au
célébrissime postulat dit des parallèles (Demande
N°5 chez Euclide, voir figure 13 ci-dessous) :
Figure 13
Demande 5 : « Et que si une droite tombant sur
deux droites fait les angles intérieurs et du même
côté, plus petits que deux droits, les deux droites,
indéfiniment prolongées, se rencontrent du
côté où sont les angles plus petits que deux droits
».
Si angle BEF + angle DFE < 2 droits (180°), les
droites AB, CD, prolongées se couperont du côté de
B, D.
Ce postulat intervient explicitement dans la preuve de I. 29(i)
et n'en est, pour ainsi dire, que la contraposée. Car si les
angles alternes AEF, EFD ne sont pas égaux entre eux, que AEF,
par exemple, est plus grand, alors AEF + BEF, soit, deux droits, seront
plus grands que BEF + EFD. Mais alors, d'après le postulat, les
droites se rencontreront. Alors que dans l'hypothèse de I. 29 on
les suppose parallèles.
Il y a tout lieu de croire que c'est
précisément pour l'usage qui en est fait ici qu'Euclide a
retenu la formulation plutôt complexe de son postulat des
parallèles. C'en est d'ailleurs le premier usage.
Autrement dit, les 28 premières Propositions du Livre I n'en
dépendent pas; elle appartiennent à ce que l'on appelle
parfois la géométrie "absolue". Si Euclide avait choisi
une formulation équivalente plus simple, telle la forme de
Playfair (« par un point non situé sur une droite, il
passe une parallèle et une seule à cette droite »),
il n'est pas certain que tant de géomètres, dès
l'Antiquité, aient essayé de démontrer cette
assertion qui, comme sa contraposée (I. 29(i)), leur paraissait avoir l'allure d'un théorème.
Mais revenons à notre proposition I. 35.
Une autre sorte d'ingrédients intervient dans sa preuve, et ce
point mérite lui aussi d'être souligné (voir figure
11 plus haut).
• Euclide part de l'égalité des deux droites
AD, EF à une même troisième, BC, pour en
déduire qu'elles sont égales entre elles. Cette
transitivité est posée dans la Notion Commune 1 :
«Les choses égales à une même chose sont aussi égales entre elles».
• Ajoutant DE à chacune d'elles, il en déduit
que AE = DF. Cette compatibilité de l'égalité avec
l'adjonction est posée dans la Notion Commune 2 :
«Et si, à des choses égales, des choses égales sont ajoutées, les touts sont égaux».
• Ayant établi (par I. 4) que les
triangles ABE et DCF sont égaux, il retranche leur portion
commune — le triangle DGE — et en déduit
l'égalité des quadrilatères ADGB, EGCF. Cette
compatibilité de l'égalité avec le retranchement
est posée dans la Notion Commune 3 :
«Et si, à partir de choses égales, des choses égales sont retranchées, les restes sont égaux».
• Enfin, pour aboutir à
l'égalité cherchée des parallélogrammes
ABCD, EBCF, il ajoute le triangle BGC à chacun des
quadrilatères. Il a donc utilisé une nouvelle fois la
compatibilité avec l'adjonction posée dans la Notion Commune 2, non plus pour des lignes, mais cette fois pour des aires.
On voit que la Proposition I. 35 requiert donc les trois notions communes
(ou axiomes) qui gouvernent certaines manipulations de la relation
d'égalité. Et nous avons vu que la preuve utilise
également le postulat des parallèles. Nous pouvons donc
dire qu'elle présuppose les principaux principes (postulats et
axiomes) du Livre I d'Euclide.
Géométrie de la mesure et fondation logique
Le déploiement de toutes ces subtilités logiques
peut paraître assez vain. Car les équivalences en aire qui
font l'objet des Propositions I. 35-41 sont absolument triviales si
nous nous rappelons les formules de calcul que nous avons apprises
à l'école :
• La surface d'un parallélogramme est le produit de sa base par sa hauteur : S = B x h.
• La surface d'un triangle est la moitié de ce produit, S = (1/2)(B x h).
Soit. Mais, précisément, comment justifier ces formules ?
Pour la seconde, c'est facile : il suffit de
montrer qu'un triangle est la moitié d'un parallélogramme
de même base et hauteur. Or c'est justement ce qu'Euclide montre,
de manière démonstrative, dans la deuxième partie
de I. 34. Quant à la première égalité, on
peut dire qu'elle est "évidente" pour un rectangle (S = L x l)
et qu'il suffit de l'étendre au cas des parallélogrammes
quelconques. C'est en quelque sorte ce qui est établi dans I.
35-36 puisque ces Propositions permettent d'affirmer que tout
parallélogramme est égal à un rectangle qui a une
base et une hauteur égales aux siennes. On peut donc lire cette
partie des Éléments comme une fondation
théorique des procédures du calcul des aires planes les
plus élémentaires, parallélogrammes et triangles.
D'autres démarches que celle d'Euclide sont possibles,
aussi bien pour justifier I. 35 que I. 47, par exemple celle de la
géométrie par "couper-coller". Celle-ci opère par
découpage et recollement, opérations d'ailleurs
utilisées dans les preuves euclidiennes de I. 35, 47. Son
présupposé fondamental est que découpage et
(re)collement n'affectent pas la somme des mêmes aires partielles
quand on la réalise de deux manières différentes
(voir figures 14-15 ci-dessous).
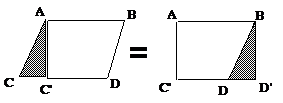
Figure 14
Cas particulier de I. 35 :
Tout parallélogramme est égal à un
rectangle qui a une base et une hauteur égale à la
sienne.
On découpe ACC'. On le colle sur BD comme BDD'.
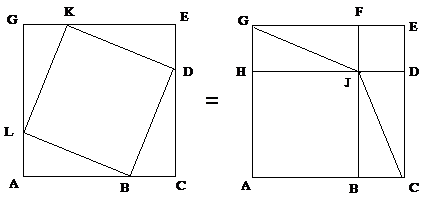
Figure 15
On pose :
AB = HJ = GF = AH = BJ = DC = EK = GL
et :
BC = JD = EF = ED = JF = GH = GK = AL
Cas particulier de I. 35 : tout parallélogramme est
égal à un rectangle qui a une base et une hauteur
égale à la sienne.
On découpe ACC'. On le colle sur BD comme BDD'.
On compare deux décompositions du carré décrit sur la droite AC, somme de AB et BC ;
• on voit que les quatre triangles BCJ, DCJ, HGJ, FGJ sont
égaux entre eux et aux quatre triangles ABL, BCD, EDK, GKL, car
ce sont des triangles rectangles dont l'angle droit est contenu par des
droites égales à AB, BC.
• Ce qui reste dans la figure de gauche, le carré
BDKL, est donc égal à ce qui reste dans la figure de
droite, les carrés ABJH, DEFJ.
Et le côté du carré BDKL est égal
à l'hypoténuse du triangle rectangle dont l'angle droit
est contenu par des droites égales à AB, BC; le
carré ABJH est le carré décrit sur AB, DEFJ est
celui décrit sur BC.
D'où le théorème de l'hypoténuse.
L'effet psychologique de conviction que procurent
ces preuves par découpage et recollement ne le cède en
rien à celui qu'engendre la démarche euclidienne. On peut
même les trouver plus expédientes. La principale
différence avec l'approche déductive est de nature
logique : la manipulation par découpage et recollement
produit une justification particulière, autonome, mais "au coup
par coup". A l'inverse, la méthode euclidienne présuppose
une démarche "rétrograde" qui n'est pas explicitée
mais qui a préalablement déterminé les
étapes successives de la chaîne déductive pour
aboutir au théorème de l'hypoténuse, en
l'occurrence : les Propositions 1 à 5, 7 à 11, 13
à 16, 18 à 20, 22-23, 26-27, 29 à 31, 34-35, 37,
41, 46, soit 29 des Propositions I. 1-46. Ce sont les «
éléments » de I. 47.
Au niveau global, cette forme euclidienne —
par contraste avec la géométrie par découpage et
recollement —, implique, pour écarter toute
régression à l'infini et pour éviter que quelque
cercle vicieux implicite ne s'introduise subrepticement, que l'on fasse
la distinction entre «ce qui n'est pas
démontré», les principes de la démonstration
et «ce qui est dérivé des principes», les
Propositions. C'était particulièrement clair dans la
Proposition I. 35, pierre de fondation des procédures du calcul
des aires rectilignes simples, dont la démonstration mobilisait
les postulats et les axiomes les plus importants de la
géométrie d'Euclide.
. 
