Souvenirs
sur Sofia Kovalevskaya
Interview / Discussion avec Michèle Audin
Après des études à l'ENS et une thèse d'état à Orsay sous la direction de François Latour, Michèle Audin est aujourd'hui professeure à l'Université de Strasbourg.
Spécialiste de géométrie et de topologie, elle s'intéresse aussi à l'histoire des mathématiques, des mathématiciens et des mathématiciennes.
La rencontre a lieu dans un grand bureau de l’Institut de Mathématiques de Jussieu. Le cadre est sobre. Une peinture à l’huile (Dame au parapluie), signée Pearson, trône sur un mur. Le décor est contrasté : une moitié du bureau est impeccablement rangée, avec des piles de documents régulièrement empilés, l’autre moitié est dans un désordre quelque peu relatif, avec beaucoup de livres anciens et quelques neufs, une boîte en nacre, un vase de fleurs. Une pile de thèses dans la première moitié est si haute qu’elle semble dans un équilibre instable. On fera attention à ne pas trop hausser la voix.
Michèle Audin retrouve Alain Chenciner,
René Cori, Rached Mneimné et Eric
Vandendriessche pour une discussion à bâtons
rompus autour de son livre, «
Souvenirs sur Sofia Kovalevskaya », paru
à la mi-automne 2008 chez Calvage
& Mounet.
Le compte-rendu est une transcription (quasi)
fidèle de la rencontre.
Michèle Audin porte un jean et une jolie
veste en cuir sur chemise
claire. Les messieurs, à l’exception de EV, sont
barbus. La barbe d’AC est
taillée avec beaucoup de soin.
MA, prête
à l’empoignade, semble trouver le rapport
de forces inégal, mais elle est visiblement prête.
AC et RM insistent sur le
fait qu’ils ne sont pas venus pour croiser le fer. Il faudra
quelques minutes à
MA pour s’y résigner, non sans quelque regret. Une
heure et demie après, la
haute pile de thèses était encore en
équilibre.
Des
mathématiques de
Sophie Kowalevski à l’histoire de Sophie
AC – Ce livre apparaît de prime abord comme un livre très personnel. D’ailleurs, lorsque Rached me l’a donné, après une demi-heure passée dessus je lui ai écrit que ce livre m’énervait ; « il y a trop de "je" » lui ai-je dit. « Continue, continue ! » m’a-t-il répondu. J’ai continué et j’ai été séduit. Néanmoins il est vrai que ce premier contact m’a fait penser que ce n’était pas un livre sur Sofia Kovalevskaya, mais plutôt sur Michèle Audin. D’ailleurs ça s’appelle « Souvenirs sur … ».
MA – C’est vrai que ce livre est un peu personnel. Comme mathématicienne, je travaille avec les mathématiques qui ont intéressé SK depuis 1991/92 (donc depuis assez longtemps). Ce que l’on appelle « le cas de Kowalevski » ou « la toupie de Kovalevskaya » est un exemple assez difficile de système intégrable, que l’on avait du mal à traiter par des méthodes de géométrie algébrique. Dans les années 1990, à peu près cent ans, donc, après la publication du papier de SK, il y a eu un article écrit par trois collègues Russes (Bobenko, Reyman et Semenov-Tian-Shansky), dans lequel ils ont récrit ce système d’une façon moderne qui le rendait ainsi susceptible d’être traité par la géométrie algébrique. C’était vraiment bien, car il s’agit d’un exemple dont la géométrie est assez compliquée. J’avais quant à moi l’idée que l’on pouvait certainement utiliser ces méthodes pour décrire la topologie, pour décrire ce qui se passe au niveau topologique et non pas juste faire de la géométrie algébrique complexe. Cet exemple était à la fois assez compliqué, assez célèbre, assez intéressant pour que cela prouve quelque chose que l’on arrive à en venir à bout. J’ai donc travaillé sur ce sujet avec Robert Silhol qui est spécialiste de géométrie algébrique réelle. C’est d’ailleurs, de toute ma carrière, le seul article que j’ai écrit en collaboration. On a donc travaillé tous les deux et publié un article en 1992 ou 93. J’étais très contente de ce travail. J’ai donc fait, et Robert aussi, beaucoup d’exposés de séminaires sur ce sujet.
Je savais que les gens pensaient que je travaillais sur ce thème parce que Sophie Kowalevski était une femme.
AC – Dans le livre, tu dis qu’il n’en est rien.
MA – Oui, effectivement. J’avais donc décidé que Sophie Kowalevski ne m’intéressait pas. Tout ce que l’on pouvait raconter sur elle, sur sa vie, ne m’intéressait pas. Pendant des années, j’ai parlé de ce sujet, j’ai essayé de faire des mathématiques en citant SK tout en faisant beaucoup d’efforts pour ne pas savoir qui était SK.
RM – Au fond, les propos de ces gens ont un peu porté ; puisque visiblement ils ont eu un effet de censure.
MA –
Non,
non ! C’est parce que je voulais juste que
ça m’intéresse parce que ce
sont de bonnes mathématiques. Point ! Et rien
d’autre ne m’intéressait.
Je refuse d’être
mise dans ce ghetto des femmes, bien que
l’on m’y mette sans arrêt !
Quand Anne-Charlotte Leffler (la sœur du mathématicien Gösta Mittag-Leffler) a écrit la bibliographie de SK à sa manière, Weierstrass a été très en colère, il a dit : « les gens meurent, ce sont les idées qui restent ».
J’étais complètement sur cette ligne-là.
Et puis petit à petit, peut-être parce que j’avais davantage de reconnaissance dans le sujet, les gens savaient que j’avais fait des choses intéressantes et je n’avais donc plus besoin de me défendre par rapport à ça. Et enfin, grâce à mon ami Jean-François Peyret, qui est apparu dans cette histoire comme un caillou dans la mare, j’ai été obligé de m’y intéresser. Et alors j’ai été séduite, car finalement SK était quelqu’un un peu comme moi.
AC – Dans l’histoire de Sofia Kovalevskaya (SK) que tu racontes, quel est le personnage qui t’a le plus mise en fureur ?
MA – Je crois que personne ne m’a mise en fureur. Ils m’ont plutôt fait rigoler. Je suis en colère contre ceux de nos contemporains qui écrivent des articles dans lesquels ils évoquent Sophie Kowalevski. Par exemple le mathématicien russe Valeri Kozlov, qui par ailleurs est un mathématicien tout à fait respectable, a écrit récemment un article [Kozlov 2000] extrêmement intéressant sur les mathématiques de Sofia Kowalevski (pour le cent-cinquantenaire de sa naissance qui a été fêté en Russie) dans lequel il glisse deux ou trois phrases de commentaire biographique absolument sans intérêt et surtout très misogynes. Cela m’a un peu fâchée.
Mais concernant des gens du début du 20e siècle, comme par exemple Gino Loria, j’ai trouvé cela plutôt rigolo.
AC – Même la réflexion du président de l’Académie des sciences de Suède ?
MA – Cette réflexion est un cadeau ! Le président de l’Académie des sciences de Suède qui dit : « Si on ne se met à considérer des candidatures de femmes, jusqu’à quels animaux de la création n’allons nous pas descendre ! » ; c’est un cadeau (pour mon livre) et je suis finalement très contente qu’il ait dit cela !
 Sophie Kowalevski
(1850 - 1891)
|
La
pièce de théâtre
de Jean-François Peyret
AC – Est-ce ton travail sur la pièce de Jean-François Peyret qui t’a décidée à écrire ?
MA – Oui. D’ailleurs le titre du livre m’a été vraiment inspiré par Jean-François Peyret, qui a dit de son spectacle que c’était un peu comme raconter « des souvenirs sur quelqu’un qu’on n’a pas connu ». En fait, je l’aurais bien appelé « Je me souviens de SK », mais la référence à Perec était tout de même trop forte.
AC – Il y a une belle référence à Perec, en particulier avec le chapitre « Je me souviens de Sophie, par Georges, Gösta, Julia et les autres», qui d’ailleurs est un très beau chapitre ; je trouve que tous ces « je me souviens » mis ensemble, c’est superbe !
RM – Pourrais-tu nous dire comment Jean-François Peyret en est venu à s’intéresser à SK ?
MA – Je vais vous dire comment lui-même raconte cela. Jean-François Peyret, qui est un grand metteur en scène de théâtre, un grand intellectuel, passait un jour devant le BHV - il aime bien, paraît-il, le sous-sol du BHV, car en tant qu’intellectuel ça lui remet les pieds dans la réalité (il dit cela mais en fait il ne va pas au sous-sol mais au premier étage, où il y a les livres !). Ce jour-là, il tombe sur le livre « Une nihiliste » [Kovalevskaya 2004]. Sur la quatrième de couverture, il voit que la personne qui l’a écrit était la femme d’un biologiste, lequel est le traducteur de Darwin en russe. Jean-François Peyret venait de monter plusieurs spectacles consacrés à Darwin : il a donc acheté ce livre.
L’auteur de ce livre est en fait SK. C’est un roman, partiellement autobiographique, qu’elle a écrit vers la fin de sa vie. Il y a quelques années, a été publiée une traduction française de ce livre. Je l’avais achetée aussi (dans une librairie plus standard que le BHV !). C’est donc comme cela que Jean-François Peyret a découvert SK. Il avait également le projet de faire un spectacle sur un mathématicien, ou plutôt sur « comment fonctionne le cerveau d’un mathématicien ». Le fait que SK fut une femme l’a certainement un peu interpellé. Il s’est mis à chercher tous ses textes, ses biographies, etc. Il n’y a pas de livre en français sur SK, excepté un livre publié par Jacqueline Détraz en 1993, qui est essentiellement le texte d’Anne-Chalotte Leffler et les souvenirs que Sophie a elle-même écrits [Détraz 1993] (avec seulement quelques pages sur les travaux mathématiques de SK).
Jean-François Peyret a pris contact avec Jacqueline Détraz, qui lui a dit de s’adresser également à moi. Il m’a téléphoné. J’étais extrêmement réticente. J’ai finalement accepté. Il m’a donné rendez-vous à Paris, à Chaillot, dans un bistro. Puis il m’a fait rentrer dans Chaillot par l’entrée des artistes… J’ai trouvé cela impressionnant !
La suite est dans le livre…
EV – Cette pièce a-t-elle eu du succès ?
MA – Elle a été donnée deux fois : à Avignon et Chaillot. À Avignon, en juillet au programme du festival, c’était plein. À Chaillot c’était en mai, et d’après Jean-François Peyret personne ne va au théâtre en mai… Ce n’était pas plein, mais il y avait un nombre raisonnable de spectateurs. En tout cas, le jour où j’y suis allée c’était le cas. À Avignon, c’était à la Chartreuse. Peyret utilise la technologie moderne, en particulier la vidéo. Il y a des acteurs qui sont présents sur le plateau et d’autres filmés en vidéo ailleurs en direct ou non. Il a utilisé le décor de la Chartreuse assez admirablement (d’ailleurs à Chaillot aussi, il a utilisé les coulisses du théâtre de façon très brillante). La musique de ce spectacle était également extraordinaire : il y avait un piano sur la scène et un musicien, Alexandros Markeas, pianiste et compositeur bien connu, qui improvisait. Le piano était relié à un ordinateur et ce qu’il jouait faisait tourner une toupie sur un grand écran. C’était vraiment très réussi. Un très beau spectacle. Ce n’était pas vraiment une pièce ; il y avait trois actrices sur le plateau, un acteur, le musicien et de temps en temps les vidéastes. C’était une réalisation technique extrêmement belle. Il y avait en particulier un moment où un texte de Poincaré sur la création mathématique était dit (un texte assez difficile) par les actrices filmées dans les loges ; elles lisaient alternativement, on ne voyait que leur bouche, c’était vraiment magnifique ! Du très beau théâtre !
J’avais
travaillé un peu avec eux ; j’ai beaucoup
aimé
le spectacle donné à Avignon. Et lorsque je
l’ai revu à Chaillot où les
conditions matérielles sont meilleures, j’ai
été vraiment impressionnée.
 "Le cas de Sophie K."
Une pièce de Jean-François Peyret |
RM – Qu’as-tu apporté personnellement à la pièce ?
MA – Probablement rien.
RM – Il t’a demandé quelques conseils ?
MA – J’ai fait deux choses. Premièrement j’ai participé à l’une des premières répétitions. Tout le monde était assis autour d’une table et j’ai fait un vrai cours de maths ; j’avais apporté une toupie, mais il y en avait déjà 50 sur le plateau ! Je leur ai expliqué la courbe elliptique, j’ai fait plein de dessins et ils me posaient des questions. À un moment donné, l’une des actrices a réalisé qu’elle n’avait jamais compris qu’un nombre négatif n’avait pas de racine carrée ; le niveau mathématique n’était donc pas très élevé.
AC – Peyret a une formation mathématique ?
MA – Non, pas du tout.
Ensuite, j’ai assisté à des répétitions : ils ont beaucoup de textes et improvisent sur ces textes. À la fin, il reste ce que Peyret appelle une partition : certains de ces textes étant conservés et d’autres pas.
Ma participation n’apparaît donc pas de façon explicite dans le spectacle mais c’était très intéressant comme travail. J’ai passé des après-midi extrêmement difficiles et intenses.
J’ai fait autre chose avec eux. Peyret a organisé quatre après-midi à la Chartreuse, qui ont eu beaucoup de succès. Il avait appelé cela « Ce soir on improvise, mais c’est l’après-midi ».
Chaque après-midi, des
scientifiques et des acteurs étaient
là : les scientifiques parlaient de sciences et les
acteurs improvisaient
sur ce qui était dit ou ce qui aurait pu être dit.
J’ai donc participé à une
après-midi sur les mathématiques, et
j’ai participé à une autre
après-midi avec
l’écrivaine A.S. Byatt, qui a écrit un
des plus beaux textes littéraires [Byatt
2003] sur les mathématiques, que
j’évoque dans mon livre (page 179), sur le
procédé diagonal de Cantor (décrit
page 143 dans le livre). Ça été
l’une des
plus grandes joies intellectuelles de ma vie : j’ai
pu demander aux
acteurs de nous lire ce texte. Devant l’auteur et
à ma demande. J’étais
vraiment heureuse. Il y avait un public qui a semblé
content ; il y a eu
une discussion.
Voilà en ce qui concerne mes expériences théâtrales liées aux mathématiques et SK.
RM – Qu’est-ce qui fait selon toi que des metteurs en scène, des auteurs de théâtre, s’intéressent aux mathématiciens ? Il y a quelques années Yasmina Reza avait aussi mis en scène un mathématicien, joué par Richard Berry (« Trois versions de la vie »). Est-ce que nous représentons pour le grand public une espèce mystérieuse, bizarre ?
MA – J’ai du mal à me mettre à la place du grand public.
AC – Quand j’ai commencé à m’intéresser aux mathématiques, j’étais tombé sur une émission de radio dans laquelle on demandait aux gens quel était le plus beau métier et lequel était le plus affreux ? Le plus beau était médecin et le plus affreux mathématicien ! J’écoutais cela avec mes parents, qui étaient médecins tous les deux, et c’est là que j’ai décidé de faire des maths !!! (Rires…)
L’éducation
mathématique de Michèle Audin
RM – Michèle, comment en es-tu venue aux mathématiques ? Ton père et ta mère étaient mathématiciens, n’est-ce pas ?
MA – Ma mère surtout. Je dis « surtout » car mon père étant mort assez jeune, c’est surtout ma mère qui a eu en charge mon éducation mathématique.
Répondre à cette question est un peu compliqué. Je suis d’une génération où lorsqu’on était bon élève, on était poussé à faire des mathématiques. Je me rappelle très bien qu’en classe de troisième, j’avais un prof de français absolument génial et un prof de math très mauvais. Moi, je voulais écrire des romans. On m’a dit « très bien, il faut donc aller en C », car « c’est là que vont les bons élèves ». J’ai donc été poussée vers les mathématiques et je ne regrette pas du tout ce choix, bien entendu.
RM – Avec ce livre, tu as fini par écrire un roman d’une certaine façon.
MA – Si l’on veut.
Les
lecteurs
non
mathématiciens - Courrier des lecteurs
AC – Bien que tu dises que ce livre n’est pas un roman, est-ce que tu as eu des retours de lecteurs non-mathématiciens ?
MA – Pour ce livre j’ai eu énormément de courriels.
Typiquement des collègues qui m’écrivent pour me dire : « j’ai acheté ton livre mais je ne peux pas le lire parce que ma femme me l’a piqué. Et maintenant il faut que je lui explique ce qu’est un sinus !». Je réponds que c’est enfin l’occasion de parler de maths avec leur femme !
AC – Tu n’as pas eu la même chose avec « mon mari » ?
MA – Non. Personne ! Par ailleurs, je n’ai pas eu de retour négatif.
RC – Mais à part dire « c’est bon ou mauvais », il ne s’est pas engagé de discussion sur tel ou tel point ?
MA –
Non.
J’aimerais tout de même signaler une remarque qui
m’a été faite à
l’occasion du
colloque organisé pour les 80 ans de l’institut
Henri Poincaré. Une personne
(au masculin) m’a interpellée en me demandant
pourquoi je n’avais pas plutôt
écrit un livre sur Emmy Noether, qui est selon lui la plus
grande
mathématicienne qui ait jamais existé. Je me suis
dit intérieurement :
« Quel dommage que le livre soit
déjà publié parce que
celle-là il aurait
fallu la mettre dedans. Ça sera dans la seconde
édition ! »
RC – Et pour tes autres livres avais-tu reçu des messages?
MA – En général, je reçois beaucoup de messages de gens qui veulent les solutions des exercices. J’ai pourtant mis sur ma page web qu’il n’y avait pas ces solutions.
AC – Peut-être devrais-tu dire que tu ne sais pas faire les exercices ! (Rires …)
MA – Oui peut-être, pour que les choses soient claires !! En fait, je sais les faire quand j’écris le livre et après je ne sais plus les faire. (Rires !)
J’ai même été contactée par quelqu’un qui était près à me payer pour avoir les solutions !!
Le
mélange (histoire,
romans, mathématiques)
AC – Bien que tu dises que ton livre n’est pas un livre d’histoire, il y a tout de même pas mal d’histoire dedans, avec beaucoup de documents. Est-ce que tu as trouvé ça plus facile ou plus difficile que de faire des mathématiques ?
MA – J’écris assez facilement. J’avais envie du mélange histoire–maths–littérature. Ce n’est pas vraiment un livre d’histoire dans le sens où il n’y a aucune source primaire (il se trouve que depuis j’ai fait vraiment de l’histoire). Même la lettre à Vollmar a déjà été publiée en allemand. La lettre de Mittag-Leffler a été publiée en russe. Donc il n’y a rien d’inédit. Et par ailleurs il y a aussi des mathématiques dans ce livre.
RM – Il y a une démarche rigoureuse qui est celle d’un universitaire, je pense, et d’une certaine façon, on voit que même si tu n’es pas historienne tu te mets dans une sorte de discipline d’exigence.
MA – Oui ! La rigueur est vraiment importante.
AC – Et la forme du livre, avec ses notes très abondantes, c’est venu tout de suite comme cela ?
MA – Oui parce que je suis quelqu’un qui fait tout le temps des parenthèses et des digressions.
RM –
Les
parenthèses étaient aussi aimées de
Roland Barthes ! Il les plaçait quant
à lui dans le texte même. Il en parle
d’ailleurs joliment dans « Barthes
par lui-même ».
AC – Par toutes ces notes où il y a souvent « je », on a l’impression que tu es contente d’écrire ce livre et que tu as envie de le dire.
Quand vas-tu écrire un roman ?
MA – J’en ai déjà écrit, mais personne ne les veut !
RM – Tu nous dis un mot de ton livre de géométrie ?
MA – Je dis toujours que j’ai écrit le Berger du pauvre [Berger 1990]. Tout ce que je sais en géométrie, je l’ai appris dans le livre de Marcel Berger. Plus précisément dans son polycopié, car le livre est sorti l’année d’après celle où j’ai passé l’agrégation. C’est un livre que j’aime beaucoup, qui est très riche ; il a aussi des tas de défauts, sa numérotation à quatre chiffres, etc. Mais il y a tout dans ce livre, il est vraiment très bien.
Mes étudiants semblaient avoir peur de l’ouvrir ; ils le trouvaient trop gros, trop compliqué,
J’ai donc essayé d’écrire le Berger du pauvre [Audin 2005].
RM – À quel moment de la journée travailles-tu?
MA – Le matin ! Je me lève à 5h et je travaille. En fait, je travaille tout le temps maintenant !
L’esthétisme
des
mathématiques
EV – Revenons à ton livre sur SK. Au début de celui-ci tu abordes l’idée de l’esthétisme en mathématiques. Tu dis à plusieurs reprises « Ces formules sont belles » ou la belle expression « asymptotes à une courbe ». Il y a également l’histoire du papier peint. Comment vois-tu cela ? « L’esthétisme dans les maths » ?
MA – C’est très facile de faire de vilaines formules. Et c’est plus difficile de faire des belles formules. Quand on a l’habitude de taper des mathématiques en TeX, on le voit très bien.
Les gens ont souvent peur des formules. Il faut leur dire qu’une formule peut être belle. Le signe « intégrale » est joli ! Ce signe a la même forme que les ouies d’un violon.
AC –
À la
page 89 de ton livre, tu expliques ce qui fait
« qu’un travail
mathématique est
intéressant ». Tu dis des tas de choses,
mais pourquoi ne
dis-tu pas simplement parce qu’il est
beau ! Moi c’est la première
chose que j’aurais dite.
MA – Tu as parfaitement raison ! C’est une erreur. C’est noté pour la prochaine édition !
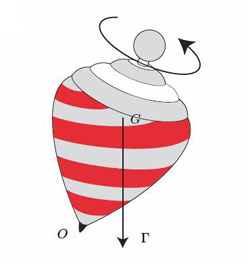
Il s’agit du chapitre où je décris le mouvement du solide, que j’ai écrit en étant un peu sur la défensive. J’ai une façon d’écrire un peu spéciale : j’écris quelque chose puis je l’épaissis. Ce texte a eu comme point de départ la préparation d’une conférence faite dans le cadre du cycle « Un texte, un mathématicien » et d’une émission de radio sur France Culture qui a précédé la conférence. Je devais expliquer simplement les choses. À la radio, c’est encore plus difficile. Il y avait la journaliste, une femme extrêmement intelligente, et Martin Andler (qui organise les conférences « un texte, un mathématicien »). Au cours de la discussion, j’ai dû expliquer pourquoi ce sujet était intéressant à des gens qui pensaient que ça ne l’était peut-être pas. Je l’ai donc pris sur la défensive.
RM –
Il y a
une très jolie comparaison avec le regard que l’on
peut porter sur une toupie.
Il y a plusieurs façons d’admirer le mouvement
d’une toupie. Un enfant va
regarder ce mouvement et trouver ça beau.
Quelqu’un comme Lagrange aura un
autre regard. Toi-même comment regardes-tu une toupie
tourner ?
MA – Il se trouve que lorsque j’ai commencé à travailler sur SK ma fille avait environ deux ans. J’ai donc été tentée de lui offrir des jouets en bois. J’ai donc à ce moment-là découvert la jubilation de la toupie. Ni moi ni mes frères n’y avions joué dans notre enfance.
Je regardais tourner cette toupie avec ma fille tout en sachant comment Lagrange la regardait. Les deux à la fois c’était vraiment agréable. Cela ne vaut pas seulement pour les toupies. Quand on regarde la nature aussi : par exemple on peut regarder un coucher de soleil au niveau zéro ou bien tout en connaissant la façon dont les nuages sont formés, pourquoi le ciel est bleu. Cela n’enlève aucun plaisir. Au contraire !
Célébrité
de Sophie –
Les récits de sa vie
RC – Est-ce qu’un étudiant, disons, en première année de mathématiques de l’Université de Stockholm, sait qui est Sofia Kovalevskaya ?
MA – C’est une bonne question. La semaine dernière, j’étais à Cornell University aux US. J’ai fait deux exposés dont l’un portait sur la toupie de SK. Il était donc annoncé que je devais parler de SK. Un collègue d’origine suédoise est venu me voir et m’a informée que généralement en Suède on sait que SK était la première femme professeure de mathématiques dans une université suédoise. Je lui ai demandé s’il y en avait eu d’autres, mais il a été incapable de répondre. Je pense donc que tous les Suédois savent cela. On leur apprend cela. Par ailleurs, je pense que Mittag-Leffler a fait un coup fumant : il a fait recruter SK… et du même coup ça a permis aux Suédois de ne plus jamais recruter de femmes !
RM – Selma Lagerlöf est tout de même plus célèbre en Suède que SK !
MA – Oui, mais elle a tout de même reçu le prix Nobel (1914) plusieurs années avant d’entrer à l’Académie. Et de plus ce n’est pas une mathématicienne, mais une écrivaine.
 Sophie Kowalevski en
1887
|
RC – Est-ce qu’on peut savoir « combien » elle est connue respectivement en Russie, en Allemagne, en France ; tu as dit qu’on a fêté (en 2000) les 150 ans de sa naissance.
MA
– En Russie
tout le monde la connaît. De son vivant, SK était
extrêmement célèbre. Tout le
monde la connaissait partout. De nos jours, en Suède, on
sait qu’elle a été
professeure à Stockholm.
En Russie, elle est
extrêmement connue et c’était donc
normal qu’il y ait de grandes
cérémonies pour le cent cinquantenaire de sa
naissance. En France, personne ne la connaît, même
nos collègues. En Russie, SK
est connue du corps scientifique, en particulier dans
l’école de mécanique
soviétique, qui a utilisé et enseigné
les travaux de SK sur la toupie (au moins
jusque dans les années 1960).
De son vivant, elle était
célèbre et reconnue dans la communauté
mathématique (par les gens qui
comprenaient ce qu’elle faisait).
Les choses ont changé
continûment après sa mort. Quantité de
choses fausses ont été écrites sur
elle. Anne-Charlotte Leffler porte une
grande part de responsabilité. Anne-Charlotte
était une écrivaine assez connue
en Suède et très amie avec SK. Elles ont
écrit des pièces de théâtre
ensemble.
Elles étaient vraiment très liées.
Quand SK est morte, Anne-Charlotte Leffler a
écrit une biographie de SK dans laquelle elle
explique de façon très
inattendue pour un mathématicien que SK était
très malheureuse de faire des
mathématiques et que ce n’était pas la
vie qu’elle aurait voulue. C’est un
discours un peu difficile à admettre pour un
mathématicien : on ne peut
pas imaginer qu’elle ait fait ce qu’elle a fait
comme mathématiques sans en
avoir éprouvé du bonheur et de la joie. Elle
était d’ailleurs, au moment où elle
est morte, très heureuse semble-t-il. Anne-Charlotte Leffler
la présente comme
quelqu’un qui aurait été
très malheureux à cause des
mathématiques, dont
la vie de femme ne s’est pas épanouie parce
qu’elle était
mathématicienne !
RM – Anne-Charlotte Leffler dit à un moment que le véritable bonheur de la femme est la recherche de l’amour, n’est-ce pas ?
MA – La recherche de l’amour fait partie du bonheur de tout le monde ; et des hommes aussi, je l’espère ! Mais les mathématiques peuvent aussi faire partie du bonheur. Et clairement pour elle, c’était le cas ! Le texte d’Anne-Charlotte Leffler a eu une assez grande diffusion, car SK était très célèbre. Il a été malheureusement pris au pied de la lettre par des gens qui ne souhaitaient pas que des jeunes filles fassent des mathématiques. Je pense par exemple à Gino Loria, historien des mathématiques (par ailleurs apparemment respectable), et surtout à Eric Temple Bell, dont le livre « Men of mathematics » a eu énormément de succès et qui est toujours lu. J’ai des collègues qui l’offrent à leurs enfants.
RM – Par exemple moi-même !
AC – J’ai constaté que Bell est cité dans l’article du « Dictionnary of Scientific Biography ».
MA – Pourtant, ce n’est pas un livre si remarquable que ça ! Il faudrait en faire une édition critique. Il y a certainement des choses très intéressantes et des tas de gens ont eu envie de faire des mathématiques en lisant ce livre. Mais d’un autre côté, il y a une sorte de « fictionalisation » de la vie des mathématiciens. Il y a deux exemples qui sont célèbres : celui de SK sur laquelle il raconte des choses absolument infâmes, et puis il y a le cas de Galois. Je dois dire que, dans ma formation de future mathématicienne, lire le livre de Léopold Infeld sur Galois a été extrêmement important. J’ai été très déçue quand j’ai appris que la réalité était différente de ce beau roman. Il faudrait faire des éditions critiques de ces ouvrages. Plutôt que de les rééditer comme ça !
RC –
Néanmoins le livre de L. Infeld a fait moins de tort
à Galois que le livre
d’Anne-Charlotte n’a fait de mal à SK.
MA – Bien sûr, Galois devait être un type insupportable, avec un mauvais caractère, qui envoyait promener tout le monde. Et plutôt que dire cela, l’auteur explique que Galois était un jeune héros incompris et révolutionnaire. Évidemment, c’est plutôt flatteur ! Alors que le portrait de SK est assez insultant comme d’ailleurs le sont aussi ceux des autres femmes qui apparaissent fugitivement dans le livre de Bell. L’histoire du chapeau par exemple, que j’ai prise à la rigolade dans mon livre, mais tout de même…
 Karl Weierstrass
(1815-1897)
|
Histoire du chapeau
MA – Quand SK était étudiante à Heidelberg, ses professeurs se sont aperçus qu’elle était douée et aimait les mathématiques. Ils se sont dit qu’elle devait aller boire la science au pied du maître lui-même. Ils l’ont donc envoyée voir Weierstrass à Berlin. Mais à Berlin ce n’était pas comme à Heidelberg : une femme n’avait pas le droit de mettre un pied dans l’Université, encore moins de suivre un cours ! Elle est donc allée voir Weierstrass pour lui demander des cours privés. Il faut imaginer cette jeune femme d’une vingtaine d’années, ne parlant pas très bien allemand. Weierstrass était une autorité. Elle était certainement intimidée. L’histoire raconte qu’elle aurait mis un chapeau afin qu’il ne voie pas qu’elle était si jeune. Elle a donc rencontré Weierstrass, qui lui a posé des questions et donné des exercices. Il a trouvé qu’elle était très douée et a accepté de lui donner des cours. Après quoi, il lui a fait passer une thèse etc.
Cette anecdote est racontée par Bell de cette façon : elle met son chapeau ; Weierstrass accepte de lui donner des cours ; et au bout de quelques séances « elle perdit son chapeau » !
Cette seule phrase est vraiment… D’ailleurs, dans la traduction française, le traducteur n’a pas osé écrire cela ! Tout est raconté dans cet esprit-là. Il y a notamment la légende colportée par Bell, et probablement inventée par d’autres, que Weierstrass et SK avaient des relations amoureuses. Ce qui n’est probablement pas vrai et n’a aucun intérêt de toute façon !
RM – Est-ce que cela aurait été un mal si tel avait été le cas ?
MA – Non, et c’est évident qu’il l’aimait beaucoup, et elle aussi. Les lettres qu’il lui écrit sont extrêmement touchantes. C’était sa « jeunesse », la plus douée de ses élèves disait-il.
Mais l’insinuation de Bell se veut justifier en partie la réussite de SK. Il faut toujours qu’elle prouve plus que les autres parce qu’elle est une femme : personne ne dirait que Mittag-Leffler a fait ce qu’il a fait parce qu’il a couché avec Weierstrass !
Femmes mathématiciennes
EV – SK a été l’une des premières femmes mathématiciennes au sens où on l’entend aujourd’hui. Ça a été parfois difficile. À plusieurs reprises dans le livre, tu sembles dire, en lançant quelques piques, que c’est toujours difficile pour une mathématicienne.
MA – En fait, ce n’est pas la première à avoir fait des mathématiques et à avoir passé une thèse. Mais SK a été la première à avoir été une mathématicienne dans le milieu académique, universitaire. Elle a été la première à être une mathématicienne professionnelle. Elle a fait exactement les choses que nous faisons maintenant. Elle donnait des cours, elle était membre d’un comité de rédaction d’un journal, elle participait à des séminaires, elle allait à des congrès. Et elle a vécu cela en faisant d’autres choses, en élevant sa fille, en écrivant des romans, etc. Il a fallu qu’elle invente le conflit entre vie familiale et carrière. Dans une moindre mesure, ces difficultés existent toujours. De façon moindre évidemment, notre vie, ma vie, a été tout de même plus facile que la sienne. Et pourtant, j’étais certainement moins bonne en maths qu’elle !
EV – Cela pose de vraies questions. J’ai rencontré récemment Véronique Slovacek-Chauveau (lire sur CultureMATH interview 2004) responsable de l’association « Femmes et mathématiques », qui s’inquiète du petit nombre de filles dans les filières scientifiques.
MA – Oui, c’est une vraie question. Pourquoi peu de femmes font des mathématiques ? Mais ensuite se pose une autre question à savoir lorsqu’une femme décide de faire des mathématiques, pourquoi doit-elle démontrer plus que les autres ?
Il faut dire également que le fait d’avoir été la seule femme mathématicienne à son époque l’a certainement aidée. Les gens s’intéressaient à ce qu’elle faisait, elle était unique. Bien que les choses soient assez différentes maintenant, j’ai déjà ressenti cela quand j’étais jeune. Le fait d’être la seule femme à faire telle recherche dans telle discipline me poussait clairement en avant. C’est le côté positif. Après il y a des tas de difficultés qu’elle a été la première à expérimenter, et que l’on continue à expérimenter.
RC – Tu considères qu’aujourd’hui une femme mathématicienne doit encore faire plus et montrer plus.
MA – Oui. Et d’ailleurs, je vais vous raconter une anecdote. Lorsque j’étais très jeune et que je cherchais un premier poste, un collègue demanda à un autre collègue qui avait écouté mon exposé, s’il était d’accord pour me rédiger une lettre de recommandation. Celui-ci répondit que non, car selon lui s’il le faisait, tout le monde aurait pensé que j’avais couché avec lui !
RC – Je suis désolé de le souligner, mais cela s’est passé il y a quelques années !
MA – Tu as raison, c’était en 1980. Mais ce n’était pas au Moyen-âge !
RC – Il y a 25 ou 30 ans j’ai entendu, dans une commission de spécialistes à Jussieu, un éminent professeur dire : « il faut qu’elle choisisse : faire des enfants ou faire des mathématiques ».
RM – Cela a beaucoup changé !
MA – Ce n’est pas tout à fait vrai : on ne dit plus ce genre de choses, mais on les pense encore !
Quand j’ai été recrutée à Strasbourg (il y a 21 ans) il n’y avait pas de femme. Ils se sont interrogés pour savoir s’il fallait vraiment recruter une femme. Finalement, la situation ressemble à la Suède du temps de SK, puisque je suis toujours la seule femme professeure à Strasbourg (en mathématiques pures) ! Ils sont contents d’en avoir une, car comme cela ils n’ont pas besoin d’en recruter d’autres !
RM – Je voudrais tout de même souligner quelque chose. De nos jours, les hommes se consacrent aussi énormément à leurs enfants. Ils sont donc beaucoup plus aptes à comprendre cette part de la vie qui est consacrée à la famille et à la relation avec les enfants. Ils comprennent donc parfaitement bien qu’une collègue consacre une partie de son temps à élever ses enfants, à s’occuper de son intérieur, à avoir des relations sociales etc. Il me semble que les mentalités ont beaucoup changé à ce sujet. Elles ont changé non parce que les hommes sont devenus plus intelligents, mais plutôt parce que les hommes se sont investis dans cette partie du quotidien qui était auparavant sous la responsabilité exclusive des femmes.
MA – Soyons clairs ! Les mentalités ont beaucoup changé, mais il y a beaucoup moins de femmes mathématiciennes aujourd’hui en France qu’il y en avait il y a 25 ans !!!
RM – Les doctorantes qui sont ici (Paris 7)…
MA – Les doctorantes qui sont ici font soit des mathématiques appliquées, ou bien alors elles n’auront pas de postes !! Des femmes qui font des thèses en mathématiques pures il n’y en a plus beaucoup.
AC – Des hommes qui font des thèses en mathématiques pures il n’y en a plus beaucoup non plus !
MA – D’accord, mais en proportion il y en a tout de même beaucoup plus !
RC – D’accord Michèle, c’est effectivement un problème. Mais je crois qu’une mathématicienne qui fait partie du petit nombre des mathématiciennes – et en effet, le fait que ce soit un « petit nombre » est problématique - qui est reconnue, qui a un poste, n’a pas à prouver chaque jour plus qu’un homme. Toi, par exemple, tu n’as pas à prouver plus que ton voisin parce que tu es une femme !
MA – Non, puisque je ne suis plus candidate à rien. Je n’ai donc plus besoin de prouver quoi que ce soit ! (Rires …)
SK a été candidate à des tas de choses. Elle a attendu très longtemps pour avoir un poste. Après un poste où elle n’était pas payée, elle a eu un poste temporaire et finalement elle a obtenu un poste permanent deux ans avant sa mort !
RC – Ce que tu démontres tout de même c’est qu’à chaque fois qu’elle obtenait des avancements elle continuait à devoir batailler pour justifier ce qu’elle avait déjà eu.
MA – Oui, bien sûr.
RC – Ce n’est peut-être plus le cas aujourd’hui. Toi, tu n’as pas à justifier ce que tu es aujourd’hui. Enfin, il me semble.
MA – Je ne sais pas si c’est le cas de toutes mes collègues.
RM – Quitte à paraître vouloir interrompre un peu votre échange, je voudrais t’interroger, Michèle, sur le mot « réputation » qui revient très souvent dans ton livre. Cela m’a interpellé. On parle rarement de la réputation d’un homme. Il y a la réputation scientifique. Tu y fais allusion. Mais j’ai l’impression qu’il s’agit dans ton propos plutôt de la réputation de la femme dans sa conduite morale ?
MA – Je n’ai absolument pas pensé à cela. J’ai pensé à Brassens et à la mauvaise réputation. Et d’autre part je pensais vraiment à la réputation scientifique.
RC – Revenons à la question de savoir pourquoi aussi peu de femmes font des mathématiques. Est-ce que tu as écrit ce livre entre autres pour dire à des jeunes filles de moins hésiter à faire des mathématiques.
MA – Oui, bien sûr ! Le point était d’expliquer qu’on pouvait être heureuse en faisant des mathématiques. C’est effectivement une des choses que j’ai essayées de faire dans ce livre.
 Gösta
Mittag-Leffler
(1846 - 1927)
|
Sophie Kowalevski et Weierstrass
RC – Je ne sais pas si le tutoiement vouvoiement existe en allemand.
MA – Il existe.
RC – Donc dans ton livre, tu rapportes un échange entre SK et Weierstrass dans lequel ils se tutoient.
MA : Absolument ! Ils se tutoient tous les deux.
RC – Tutoie-t-elle Mittag-Leffler également ?
MA – Non. Il faut noter que Weierstrass ne tutoyait aucun de ses élèves. SK a été assez proche de Weierstrass. En tout cas assez proche pour lui raconter que son mariage était un mariage blanc. Il a alors compris qu’elle ne faisait pas des mathématiques comme cela, mais qu’elle avait besoin d’un diplôme pour ensuite trouver du travail. C’est à partir de ce moment qu’ils se sont tutoyés.
AC – D’ailleurs, il signe « ton Weierstrass ».
MA –
Oui ! Il avait une relation très
particulière avec elle. Au minimum, il la
considérait vraiment comme sa fille. Ils avaient une
relation très amicale et
très forte. On sait qu’il la tutoyait car bien
qu’il ait lui-même brûlé
toutes
les lettres de S après sa mort, l’une
d’entres-elle a été
retrouvée par miracle
par Reinhard Bölling. Ce dernier était un chercheur
est-allemand (au temps de
l’Allemagne de l’Est). En janvier 1990, juste
après la chute du mur de Berlin,
il est allé à l’institut
Mittag-Leffler, où il a enfin pu étudier les
documents
concernant SK conservés dans cet institut. Il a ouvert un
dossier dans lequel
il y avait des documents relatifs aux obsèques de S et le
bouillon d’une lettre
que SK avait envoyée à Weierstrass dans laquelle
elle le tutoie.
Les étudiants de Sophie Kowalevski
RC – Il y a dans le livre assez peu de choses sur les étudiants de SK. Y a-t-il peu de documents, peu de renseignements ? Il y a un passage où tu fais allusion à sa façon de faire cours.
MA – Oui, il y a quelques documents dans lesquels des étudiants racontent comment elle était en cours. Il est dit notamment qu’elle recevait des cadeaux car ses cours étaient bien. Elle n’a pas eu (on le saurait) d’étudiant qu’elle aurait fait travailler sur un sujet dans le cadre d’une thèse.
RC – J’ai fait une recherche sur « The Mathematics Genealogy Project » et on y trouve le nom d’Emil Stenberg, finlandais, qui aurait fait une thèse dirigée par SK, soutenue en 1885.
MA – Je n’en avais pas entendu parler. Il faudra le mettre dans l’édition suivante du livre. Mais avant, il faudra vérifier car il y des erreurs sur ce site.
RC – Quelle est selon toi la raison pour laquelle SK n’a pas eu (davantage) d’étudiants. Est-ce qu’elle était trop jeune ? À quel âge dirigeait-on des thèses à cette époque ?
MA –
À cette
époque, le statut de directeur de thèse
n’existait pas. Elle aurait pu avoir
des étudiants, c’était
quelqu’un de reconnu, elle écrivait des rapports,
des
lettres de recommandation, etc. Donc je ne sais pas pourquoi.
Les mathématiques du livre
MA – Il y aussi la question des mathématiques qui sont dans ce livre. Je prétends qu’il peut être lu, en sautant quelques passages, par quelqu’un qui ne fait pas de mathématiques.
AC – ça, je n’y crois pas !
MA – J’ai le témoignage d’un lecteur : Jacques Roubaud.
AC – Mais il a une thèse de mathématiques !
MA – Laisse-moi finir ! Il a lu ce livre en se disant qu’il y avait trop de mathématiques et donc que personne ne pourrait le lire. Mais finalement, il m’a dit qu’il trouvait vraiment bien qu’il y ait toutes ces mathématiques dans le livre. Selon lui, le lecteur non mathématicien (qui ne lira pas ces parties) serait convaincu lorsqu’il est dit que les travaux mathématiques de SK sont excellents. (Sourires)
AC – Sur ce point je suis d’accord. Mais ce n’est pas lisible par n’importe qui.
MA – C’est peut-être lisible en sautant les mathématiques.
AC – Je ne sais même pas si les mathématiques de ce livre sont compréhensibles pour nos étudiants de licence.
MA – Probablement pas. Mais ils peuvent sauter quelques pages et regarder les images. Il y a de jolies images.
AC – Cauchy est superbe ! Il a bien l’air d’un baron.
MA – Et Lagrange, le pauvre, qu’est-ce qu’il a l’air triste.
AC – Moi, j’ai été très heureux des mathématiques qui sont dans ton livre. C’est d’ailleurs la raison pour laquelle je me suis dit qu’ayant aimé lire ces mathématiques elles n’étaient certainement pas pour un lecteur non mathématicien.
RM – Peut-être parce que tu vois plus que nous ce qu’il y a derrière. Ce sont peut-être encore des regards différenciés, comme on regarde la toupie. D’ailleurs Alain, ton avis m’importe beaucoup : comment vois-tu les mathématiques de ce livre ?
AC – Ce sont des mathématiques que j’aime beaucoup. Je trouve que Michèle a fait un gros effort pour raconter ces choses passionnantes. En particulier, les figures pour montrer où interviennent ces courbes elliptiques ou hyper-elliptiques. Pour quelqu’un qui connaît le domaine c’est un très joli résumé des idées. Elle nous dit même qu’il y a encore des mystères : pourquoi le fait que ces solutions soient méromorphes implique-t-il qu’il y a une intégrale première ? Pourquoi y a-t- il une courbe de genre 2, une courbe de genre 3, etc. ? Il y a plein de problèmes. J’ai trouvé très joli d’arriver à mettre tout cela dans ce bouquin.
Tu t’es beaucoup attachée à la toupie, qui correspondait à ton travail. Je ne sais pas si tu avais lu l’article sur SK dans le « Dictionary of Scientific Biography ». Moi, il m’a sidéré. Il ne parle pratiquement pas de ce travail sur la toupie qui est considéré aujourd’hui comme le plus important. Il en dit juste quelques mots. L’auteur manifestement n’y comprend rien et elle dit juste que ce travail est en rapport avec les intégrales hyper-elliptiques. Finalement, elle parle surtout de Saturne, ne parle pas de l’erreur trouvée par Volterra, et ne parle donc pratiquement pas de ce qui est son plus beau travail.
MA – Oui, tu as raison. Mais dans le « Dictionary of Scientific Biography », il y a parfois des choses étranges. Par exemple, lisez l’article sur Fatou où il n’est pas question de ses travaux sur l’itération des fractions rationnelles non plus.
C’est amusant que les anneaux de Saturne prennent une si grande place.
AC – Poincaré parle tout de même dans plusieurs mémoires de SK en disant que c’est elle et lui qui ont démontré que ça existe.
MA – Mais c’était de la mécanique des fluides et l’on savait déjà que l’on ne pouvait pas considérer les anneaux de Saturne comme un fluide.
AC – Oui, mais je crois qu’elle se fiche des anneaux de Saturne ; elle regarde le problème de mécanique des fluides puis elle montre que l’on peut calculer les développements jusqu’à n’importe quel ordre. C’est tout de même un article important.
MA – Oui. C’est un joli « truc » les anneaux de Saturne. Il y a cette astronome Dorothéa Klumpke qui a continué à travailler sur ce sujet.
AC – Ce qui est curieux c’est que cet auteur russe ne la cite pas.
MA – Klumpke est aussi quelqu’un d’intéressant. Elle a arrêté de faire des mathématiques et a continué à donner de l’argent à l’Observatoire pendant longtemps.
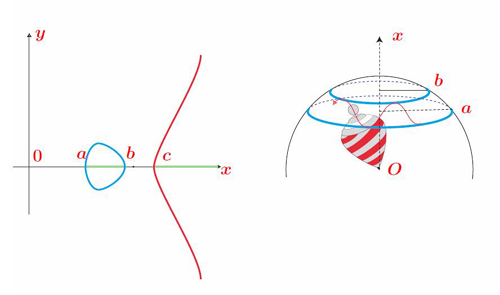 Courbe de elliptique
de genre 1 -
Nutation de
l'axe de la toupie
|
La
difficulté du
travail mathématique
RC – On ne se rend peut-être pas assez compte en lisant ce livre de la quantité et de la qualité du travail que tout cela suppose. J’essaye de me mettre à la place d’un jeune qui ouvre ce livre : je ne suis pas persuadé qu’il mesure l’étendue de la tâche. Tout ce que représente le travail qui mène à la publication d’un article de mathématiques.
MA – Tout de même ! SK dit qu’elle pense à cela depuis les années 1872, qu’en 1884 elle écrit une lettre à ce sujet et que finalement, en1888, elle écrit un article. Que ce travail est nouveau. Qu’il y a 50 pages de calculs pour réussir à écrire les solutions ! Je n’ai donc pas cette impression, mais par ailleurs je ne suis pas lectrice du livre. Peut-être ai-je une mauvaise appréciation, mais j’ai l’impression d’avoir essayé de mettre cela dans le livre.
RC – Il y a deux chapitres de mathématiques dans lesquels on ne peut pas ne pas mesurer l’effort que tout ceci suppose. Mais sur l’ensemble du livre, je ne suis pas sûr ; d’autant plus que certains lecteurs ne s’attarderont pas sur les deux chapitres de mathématiques.
RM – En tout cas le message que tu veux, mon cher René, faire passer c’est que pour faire des maths il faut bosser !
RC – Et ces gens-là bossaient comme des dingues !
RM – Et nous continuons à le faire !
AC – C’est vrai que nous passons tous notre vie à travailler.
RC – Ce que je voudrais dire c’est que pour nous cela va de soi. Mais je ne suis pas sûr que pour un lecteur lambda cela soit le cas.
AC –
Moi je
ne suis pas capable de me mettre dans la peau de quelqu’un
qui n’a pas fait de
mathématiques pendant 40 ans…
MA – Cela rejoint ce que disait Jacques Roubaud : le lecteur voit que j’ai écrit beaucoup de maths, donc il va penser que tout ceci est difficile !
Paul Painlevé
RM – Il y a la photo de Paul Painlevé dans ton livre. Il y a depuis longtemps un square à Paris qui porte son nom. C’est un personnage qui revient un peu à la mode. Quelle est la place de Painlevé dans l’histoire de SK ?
 Paul Painlevé (1863
- 1933)
|
MA – C’est marginal. Il y a quelque chose aujourd’hui qu’on appelle la propriété de Painlevé qui a plus ou moins été utilisée pour la première fois par SK.
AC – C’est cette propriété qui était d’abord dans l’article d’Adler et Van Moerbeke sous le nom de Kovaleskaya et qui a disparu ensuite.
MA – Oui. Ils ont tout d’abord publié un article dans lequel ils l’ont appelée « Propriété de Kowalevski ». Quelques années plus tard, elle est devenue « Propriété de Kowalevski – Painlevé ». Puis ils ont publié un livre dans lequel il n’y avait plus que le nom de Painlevé.
AC – C’est tout de même extraordinaire !!!
RM – Painlevé a été ministre de la guerre.
MA – Bien après ! Painlevé est un personnage intéressant. Il s’est arrêté de faire des mathématiques relativement tôt au début du 20e siècle en raison d’un problème personnel.
Un deuil me semble-t-il. Puis il s’est mis à faire de la politique. Il a été premier ministre un moment pendant la première guerre mondiale. Il a donc eu un rôle politique non négligeable au début du 20e siècle. Il a créé la Direction des inventions : les mathématiciens se sont mis à travailler pour l’effort de guerre grâce ou à cause de lui.
C’est quelqu’un qui a fait de belles mathématiques. Il connaissait bien les équations différentielles et il a inventé des tas de choses très belles, dont les équations que l’on appelle maintenant les équations de Painlevé.
Il était un peu plus jeune que SK. Donc lorsqu’il est arrivé dans le milieu des équations différentielles, SK était déjà célèbre. Je trouve qu’il est un peu condescendant avec elle quand il en parle ; mais cela me semble de bonne guerre : il était plus jeune et il voulait se faire une place parmi les gens déjà installés.
AC – Poincaré, lui, n’est pas condescendant.
MA – Oui, mais Poincaré n’avait rien à prouver !
AC – Certes, mais il dit « j’ai repris la méthode de Mme Kowalevski ».
MA – Poincaré était quelqu’un de bien.
 Henri Poincaré (1854
- 1912)
|
Après la mort de Vladimir
RM – Je voudrais parler d’un passage de ton livre que je trouve important : quand le mari de SK, Vladimir Kowalevski, se suicide, elle est malade pendant quelques jours. Elle est extrêmement malheureuse. Puis un jour elle commence à griffonner des formules et se met à faire des mathématiques. Tu dis que c’est « une leçon à méditer ». Est-ce que cela veut dire que tu vois dans les mathématiques comme une guérison possible face aux souffrances de la vie ?
MA – Je n’ai pas dit tout à fait cela : mais plutôt « une belle histoire édifiante ».
AC – Je suis un peu étonné de la question ! Cela me paraît évident que si vous êtes passionné par les mathématiques, elles deviennent une de vos raisons de vivre.
RM – Oui, mais ma question est : y aurait-il une dimension consolatrice dans les mathématiques ? Trouverait-on une sorte de consolation en faisant des mathématiques lorsque l’on est en souffrance ?
MA – Pourquoi pas ?
AC – Sans doute oui. Mais de même qu’un écrivain trouverait de la consolation en écrivant.
RM – Le mot « édifiant » n’est pas innocent.
MA – Oui, je trouve « édifiant » qu’elle n’ait rien fait pendant 5 jours et que la première chose qu’elle ait faite soit des mathématiques.
RM – J’ai une autre question derrière celle-là. Lorsque son père meurt, elle trouve de la consolation en consommant son mariage ?
MA – On ne sait pas vraiment. C’est ce qu’on raconte…
RM – Alors qu’est-ce qui est le plus consolant ?! Il fallait bien arriver à la troisième question !! (Rires)
MA – Bon, faisons le point sur cette affaire. Elle a fait un mariage blanc et il semble que cela se soit bien passé avec son mari dans le sens où ils s’entendaient bien et étaient d’accord sur ce mariage blanc. Il est probable qu’il est tombé amoureux d’elle. Et ça n’a pas été un mariage blanc tout le temps puisqu’ils ont eu une fille assez tardivement. Anne-Charlotte Leffler raconte que ce serait lorsque le père de SK est mort qu’elle et son mari auraient couché ensemble pour la première fois. Moi je veux bien, mais je crois que l’on n’en sait rien. Personne ne peut savoir une chose pareille ! Et ça n’a pas grande importance. En revanche, on sait qu’ils ont eu une vie amoureuse assez difficile. Apparemment, lorsqu’ils sont vraiment devenus mari et femme leur relation a changé. Vladimir s’attendait à ce qu’elle se comporte désormais comme une épouse et non plus comme une camarade qui continue à faire ses études et à vivre sa vie. Ce n’était pas franchement la tasse de thé de Sophie. Je pense qu’ils avaient beaucoup d’affection l’un pour l’autre, mais ils n’ont pas réussi à vivre ensemble. Ils ont donc eu une vie extrêmement difficile et agitée. Ils se sont séparés puis retrouvés. Je crois qu’ils s’aimaient beaucoup lorsqu’ils étaient loin l’un de l’autre mais qu’ils avaient du mal à se supporter.
Lui a eu d’autres problèmes : il a eu du mal à trouver un boulot et il a perdu tout son argent et celui de Sophie ; et il a fini par se suicider. Je pense que Sophie en a beaucoup souffert même si elle n’était pas une épouse modèle.
Elle en a beaucoup souffert, mais elle en a aussi bénéficié. Car à l’époque, la seule façon pour une femme d’être adulte et majeure était d’être veuve. Dès que son mari est mort, Mittag-Leffler et Weierstrass se sont mis à penser à lui trouver un poste. C’est donc à ce moment-là que l’on a commencé à la considérer comme une professionnelle. Je fais remarquer que ce fut aussi le cas pour Marie Curie, qui a obtenu un poste après la mort de son mari.
Le statut de veuve était la seule façon pour une femme d’être majeure. Et c’est encore comme cela pour des jeunes femmes de l’autre côté de la Méditerranée, par exemple.
RC – Je reviens sur le mariage blanc de Sophie. Tu as l’air de dire que la pratique des mariages blancs était très courante.
MA – Oui, dans ces milieux-là, ça se faisait.
RC – Cette pratique était connue et tolérée de tout le monde, ou bien cherchait-on à les embêter ?
MA – Ces mariages blancs n’étaient bien sûr pas annoncés comme tels. Sophie s’est mariée en blanc. Elle a forcé la main à son père en faisant quelque chose de nuisible à sa réputation. Son père ne voulait pas de ce mariage. Malgré cela elle est allée chez son futur époux et son père n’avait donc plus le choix : il fallait qu’il marie sa fille pour sauver sa réputation. Elle s’est mariée en robe blanche. L’une de ses tantes a témoigné en disant qu’elle était belle, heureuse et amoureuse. Donc personne ne savait que c’était en fait un mariage blanc.
On comprend bien ce qu’une jeune fille gagnait par ce type de mariage. Par contre, je ne vois pas bien ce que cela apportait au jeune homme. À moins de faire cela par militantisme : ces gens avaient dans l’idée que le peuple avancerait par l’éducation. Il était donc important d’éduquer les gens et en particulier très important d’éduquer les femmes. Cette idée est très fondamentale : la vie s’améliorerait quand les femmes seraient mieux éduquées. C’est maintenant quelque chose que nous savons et nous voyons bien que, dans certains pays, les choses avancent grâce à l’éducation des femmes.
C’est un fait que ces gens-là ont inventé à l’époque. Il y a 150 ans.
À Alger
RM – Tu as offert cinq exemplaires de ton livre à l’Université d’Alger : pourquoi Alger et pas Abidjan ou Dakar ?
MA – C’est l’éditeur qui a proposé d’offrir des livres à une université en Afrique et j’ai choisi Alger. J’ai des liens avec l’Algérie : j’y suis née. Ce sont des liens très distendus, car je refusais d’y aller depuis longtemps jusqu’à l’année dernière où je n’ai pas été capable de refuser. Je suis allée faire un cours dans une école d’été qui se tenait à Tipaza, non loin d’Alger. On m’a aussi proposé de faire un exposé très grand public à l’université d’Alger (un peu comme celui que j’avais fait à la BnF - Le cas de Sophie Kowalevski). À mon arrivée, j’ai été reçue par le président (on dit le « Doyen », je crois) qui a présenté la conférence. C’était dans une très grande salle remplie d’étudiants et d’étudiantes dont la plupart étaient voilées (mais pas toutes). Ce fut un peu difficile pour moi, car le Doyen m’a présenté comme étant la fille d’un homme faisant partie de l’histoire de l’université. Ce fut donc un peu dur de commencer une conférence dans des conditions pareilles. Mais bon, je l’ai fait.
À la fin de la
conférence il y a eu des questions : un
collègue algérien m’a
demandé comment SK était devenue professeure. Je
me suis
donc retrouvée devant toutes ces jeunes filles, toutes
mineures, soumises à
leur père, puis à leur mari, à
expliquer qu’à l’époque si on
voulait faire des
études à l’étranger, il
fallait y aller avec son mari et que l’on devenait
majeure lorsqu’on était veuve. Je me sentais
vraiment très mal ! Et donc
j’ai souhaité que ces jeunes filles lisent ce
bouquin.
Les métamorphoses causées par le mariage
RM – Une question concernant deux passages de ton livre où tu parles de la métamorphose des hommes et des femmes après le mariage. Quels conseils donnerais-tu à de nouveaux mariés dont l’un des deux est mathématicien ?
MA – Entourée d’une majorité d’étudiants hommes pendant mes études, j’ai eu le manque d’originalité de choisir un ami mathématicien. L’avantage pour moi est qu’il sait que je peux être assise sur une chaise en ayant l’air de ne rien faire mais pourtant être en train de travailler. Je conçois que ce n’est pas évident à comprendre pour quelqu’un qui travaille à heures fixes, un ingénieur par exemple. On peut rester chez soi, parfois même on reste au lit, mais on est tout de même en train de travailler. La vie est donc plus facile avec un conjoint qui comprend que ce n’est pas parce que l’on reste à la maison que l’on est disponible.
RM – Je voudrais faire allusion à un passage qui m’a interpellé. Il s’agit de la métamorphose de certains individus dans le mariage.
MA – Il est dit dans le livre qu’il y a des femmes mathématiciennes qui se sont métamorphosées en femmes au foyer en se mariant. Et des maris qui se métamorphosent en hommes exigeant de leur femme d’agir ainsi. C’est quelque chose que je ne comprends pas. C’est un fait d’expérience. J’ai été étudiante dans une école où il y avait beaucoup des filles (l’École normale supérieure de jeunes filles) et je connais beaucoup de jeunes mathématiciennes qui sont devenues des femmes au foyer ; je connais aussi beaucoup de mathématiciens qui ont épousé ces jeunes mathématiciennes et qui les ont transformées en femmes au foyer. Ils vivent parfaitement heureux comme cela. Mais c’est un phénomène social que je ne comprends pas.
RC – Tout cela ne me semble pas spécifique aux mathématiciens et mathématiciennes ?
MA – Certainement, je ne suis pas sociologue. Mais je constate et regrette que, dans mon milieu, ça soit souvent ainsi. Et cela est incontestablement favorisé par ce que j’évoquais plus haut : puisque qu’on travaille à la maison en horaires libres on n’a qu’à s’occuper des gosses et faire les courses !
Par ailleurs, je n’ai jamais dit que tous les mathématiciens ne faisaient jamais les courses…
AC – On pense très bien aux mathématiques en faisant les courses, ou en faisant la vaisselle…
MA – Oui, la vaisselle est le cas typique d’une activité qui favorise la réflexion.
Engagement
politique
de SK
RC – As-tu une idée du degré de l’engagement de SK dans des combats politiques à Paris, en Allemagne ?
MA – À Moscou, elle appartenait à un groupe nihiliste. Elle est ensuite allée à Paris pendant la Commune, parce que sa sœur y était et elle et son mari étaient inquiets. Sa sœur est mentionnée dans les histoires de la Commune comme ayant participé aux mouvements des femmes. Le mari de sa sœur était aussi un communard ; il a été condamné à mort. SK a servi comme infirmière pendant la Commune ; donc pendant une période très courte. Comme vous le savez, la Commune n’a pas duré plusieurs mois mais juste quelques semaines.
AC – Oui. Tu fais une remarque à ce sujet dans le livre.
MA – Je dois dire que c’est difficile de lire : « SK a passé plusieurs mois à Paris pendant la Commune… ». La Commune a commencé le 18 mars, et le 28 mai ils étaient tous morts !
Je suis une grande admiratrice des communards et notamment des femmes de la Commune.
Sa contribution a
été de parler avec des gens ; elle
était notamment très amie avec des
révolutionnaires polonais ; elle était
dans un cercle de révolutionnaires russes et polonais
lorsqu’elle vivait à
Paris.
RC – Elle n’a pas cassé les caténaires des trains?
MA – Non elle n’a pas fait cela. Mais elle a défendu la cause des femmes bien que je ne sache pas vraiment comment.
L’article erroné de Sophie
RC – Tu racontes l’histoire de son article erroné d’une façon convaincante. Tu montres bien que cette erreur que SK a faite dans un article a été utilisée de façon pas très correcte contre elle ! Tu cites un commentaire d’Hermite qui transmet la note à l’Académie des sciences : « Les recherches mathématiques de Mme Kowalevski sur la physique mathématique ont eu pour objet la propagation de la lumière […] Un si rare talent, une telle supériorité d’intelligence me font vivement désirer que dans l’intérêt de son enseignement mathématique l’Université de Stockholm s’assure le concours de Mme Kowalevski ». Et en marge tu écris : « Je saute ici les compliments sur un travail qui va s’avérer erroné ».
Je me demandais si tu avais eu vraiment raison de les sauter. Parce que citer des commentaires élogieux d’Hermite sur un travail erroné ça me paraît être un excellent argument en faveur de ta thèse qui est que l’on s’est beaucoup trop servi de cette erreur contre elle. Après-tout, le fait que quelqu’un comme Hermite soit capable, au moment où le travail est proposé, de faire des commentaires extrêmement élogieux relativise l’importance de cette erreur. Et montre que ceux qui l’ont exploitée de façon éhontée ont certainement eu tort !
MA – Tu as raison, mais je ne pense pas qu’Hermite ait lu le papier très sérieusement. Par contre, ce qui est sûr, c’est que Weierstrass l’a lu ! Runge aussi l’a lu, Sophie l’a lu avec lui. Je le raconte dans le livre. Ils ont travaillé un été. Il l’a aidée à corriger l’allemand, à corriger des fautes. Je ne suis pas absolument certaine qu’Hermite lisait tous les papiers qui passaient à l’Académie des sciences. Et c’est pourquoi je n’ai pas insisté sur ce point.
AC – À propos de Hermite : je suis allé voir la correspondance de Hermite et Stieltjes.
Il y a une lettre adorable d’Hermite à Stieltjes qui lui dit en substance : « Je suis très embêté, car j’ai reçu de l’université de Stockholm une demande de rapport sur les travaux scientifiques de Madame Kowalevski. J’ai du mal à le faire. Pourriez-vous m’aider ? »
Je me suis donc demandé si tu aviais vu une lettre ou un rapport de Stieltjes. Il y a une réponse de Stieltjes qui dit qu’il va surtout s’attacher au mémoire paru dans Astonomische Nachrichten sur Saturne et sur celui du Journal de Crelle sur les intégrales.
MA – Comme je l’ai dit tout à l’heure il n’y a pas de sources primaires citées dans ce livre. Maintenant que j’ai pris l’habitude (depuis que j’ai écrit ce livre) de fréquenter les archives de l’Académie des sciences, je regrette beaucoup de ne pas y être allée plus tôt.
Ils se sont tous mobilisés pour qu’elle ait un poste et cela vaudrait la peine d’aller regarder ces correspondances.
AC – Hermite écrit : « Les mémoires de Mme Kowalevski étant écrits en allemand, sauf celui qui a été couronné récemment par l’Académie des sciences, je viens vous demander de me sortir d’anxiété et de me tirer d’un extrême embarras… ».
MA – Hermite est un épistolier délicieux, comme dit ma collègue Catherine Goldstein.
RC – N’est-il pas possible que cet embarras soit dû au fait qu’il a des doutes sur le travail erroné de SK ?
MA – Non. Personne ne s’était aperçu de l’erreur. C’est Volterra qui, après la mort de Sophie, s’est aperçu qu’il y avait une faute dans cet article. Il était très jeune.
 Charles Hermite
(1822-1901)
|
Ce
livre et
les
professeurs de mathématiques
EV – Que peut apporter ton livre aux professeurs de mathématiques du secondaire ? Y as-tu pensé en l’écrivant ? Car, par les professeurs de mathématiques du secondaire, les idées que développe ce livre pourraient être disséminées dans les jeunes générations.
MA – Il y a deux choses : les mathématiques et le reste.
J’ai été confrontée à cette question l’autre jour pour l’exposé que j’ai fait dans le cadre du séminaire de l’IREM Paris 7 ( Vidéo de la conférence). J’ai raconté dans l’introduction que deux élèves de première du lycée Victor Duruy avaient écrit à l’association « Femmes et mathématiques » en expliquant qu’elles souhaitaient faire un TPE sur SK, qu’elles avaient lu l’article de Michèle Audin dans « Tangente », qu’elles n’avaient rien compris et demandaient conseil pour trouver d’autres documents.
« Femmes et mathématiques » en la personne de Véronique Chauveau m’a donc contactée. J’ai travaillé dans un groupe IREM sur les TPE (travaux personnels encadrés) pendant assez longtemps, du temps où les TPE avaient aussi lieu en terminale. Nous nous étions rendu compte qu’il était difficile de faire des TPE, avec par exemple des équations différentielles, pour des élèves de terminales qui savent tout juste ce qu’est une dérivée. Ma réponse a donc été qu’il valait mieux que ces élèves changent de sujet. Je pense que les mathématiques de SK sont trop difficiles pour des élèves de première et même de terminale parce que le premier outil est toujours une équation différentielle. En général, celle-ci est assez compliquée, ça peut être une équation aux dérivées partielles comme pour le théorème de Cauchy–Kowalevski, ou bien un système d’équations aux dérivées partielles ; c’est donc trop difficile !
En revanche le fait que des professeurs de mathématiques sachent qu’il y a eu des femmes qui ont fait des mathématiques et qu’elles ont été heureuses d’en faire me semble une bonne chose. Dans les manuels scolaires lorsqu’il y a la photo ou l’image d’un mathématicien, c’est toujours (ou presque) un vieux barbu ! Je n’ai rien contre les barbus, ni les vieux, mais bon…
AC – Ah non ! Il y a tout de même le buste de Fermat à Toulouse avec une femme déshabillée qui lui tend un crayon (Rires…)
MA – Je ne vois jamais Fermat ! Dans le meilleur des cas, je vois Euclide et Pythagore, qui n’étaient probablement pas barbus, mais qui sont représentés comme tels. Dans le chapitre sur les équations différentielles des livres de terminale, peut-être pourrait-il y avoir la photo d’une femme. Si les professeurs de mathématiques savent qu’il y a eu des femmes mathématiciennes qui ont travaillé sur ce thème, peut-être en parleront-ils à leurs élèves.
Mais quant au contenu « mathématique », c’est trop difficile. D’ailleurs il en est de même de Poincaré…
RC – C’est évidemment beaucoup trop difficile pour des élèves. Mais pour que les professeurs soient accrochés il faut qu’eux-mêmes puissent entrer dans les maths de SK. Tu as l’air de considérer que même pour les profs de maths, c’est trop difficile.
MA – Non pas du tout ! J’ai écrit un article pour « Tangente » (Tangente 109, mars-avril 2006 p 26-29) qui est non seulement accessible aux profs mais visait les profs, voire des étudiants de premier cycle.
Il y a donc des mathématiques de SK que l’on peut expliquer aux professeurs de mathématiques. D’ailleurs, n’ai-je pas fait une conférence à L’IREM de Paris 7 ? Mais il est vrai que je n’ai pas parlé de la « toupie ».
AC – C’était sur le théorème Cauchy-Kowalevski qui semble plus facile à raconter que la « toupie ».
MA – Quoi que j’aime bien le dessin avec la courbe elliptique (pages 95 et 98).
AC – Oui, mais si on ne sait pas qu’une courbe elliptique est un tore…
MA – Non, on n’a pas besoin de cela. Je parlais du petit ovale qui bloque l’axe de la toupie entre les deux cercles parallèles. Il n’y a pas besoin de complexes pour faire cela. J’en parle d’ailleurs dans l’article dans Tangente.
EV – En ce qui me concerne cela m’a pris un peu de temps pour rentrer dans les maths de SK que tu décris dans ces deux chapitres. J’avais étudié cela, il y a une vingtaine d’années dans le cadre des cours de DEA de Boutet de Monvel et Vaillant. Je conçois que si quelqu’un n’a pas réfléchi à la résolution de systèmes différentiels depuis un moment cela puisse poser quelques difficultés.
MA – Oui, ce sont des maths difficiles. C’est vrai.
EV – Je pense néanmoins qu’il y a là un enjeu intéressant que CultureMath ou les IREM, il me semble, voient aussi comme tel : ces notions ne sont pas très loin dans la tête des enseignants et finalement il suffit de réactiver quelques liens pour leur donner accès à ces idées. J’ai le sentiment que lorsqu’on a fait des mathématiques à un certain niveau (peut-être y a-t-il un point de non retour, c’est possible, c’est ce que disent certains chercheurs en neurosciences comme Changeux par exemple) il doit en rester pas mal de choses. Il suffirait de réactiver un peu ses neurones ; ça demande effectivement du travail, de l’énergie, mais cela est possible !
AC – Réactiver demande toujours du travail : on a tous fait l’expérience de relire un de ses propres articles écrit il y a plusieurs années en arrière et devoir travailler pour le re-comprendre.
EV – Ce que je voudrais dire c’est que des lieux, comme le séminaire de l’IREM de P7 par exemple, existent pour que des enseignants continuent à faire des mathématiques. Cette discipline est une des rares disciplines, et cela a été dit au « Colloque sur l’avenir de l’enseignement de mathématiques » (novembre 2008), où les enseignants cessent souvent de faire des mathématiques au-delà du programme de terminale. Parfois ils ont envie de faire ou refaire des maths mais cela leur demande beaucoup d’énergie. J’ai l’impression que ce genre d’ouvrage pourrait donner envie aux enseignants (au même titre qu’une conférence dans un IREM) de refaire des mathématiques.
AC – Est-ce que dans la production éditoriale actuelle il y a des bouquins qui peuvent se comparer à celui-là, qui seraient dans la même catégorie ?
RM – Il serait difficile d’en faire l’inventaire. J’ai remarqué un bouquin sur Euler à l’occasion du tricentenaire de sa naissance, avec un peu de mathématiques dedans. Il y a eu des livres de vulgarisation sur le théorème de Fermat [Singh 1999] et il y a eu aussi un livre sur Hadamard (Voir le résumé) . Plus récemment, il y a eu un livre qui raconte en photos les mathématiciens de l’IHÉS, et ayant pour titre « Les déchiffreurs »(Voir le résumé).
Vulgarisation
des
mathématiques vs Vulgarisation de la physique
EV – Tout ceci pose le problème de la vulgarisation des mathématiques. Est-ce que les mathématiques sont suffisamment vulgarisées ? Doit-on chercher à sensibiliser un maximum de gens aux idées mathématiques, même les idées profondes ? Est-ce possible ?
MA – C’est possible et ça vaut le coup ! Mais il faut dire « On va raconter des mathématiques intéressantes avec des idées profondes à tel niveau et en choisissant ce niveau ». Dans le cas de SK, on part d’un niveau qui est déjà fixé. Cela dit j’ai déjà raconté l’« histoire » de la toupie devant des élèves de terminale dans un lycée très lambda de l’île de la Réunion, à trois classes de terminale dans un amphi, entre deux champs de cannes à sucre. Ils faisaient les mariolles avant d’entrer. Je me suis demandée comment ça allait se passer, et puis j’ai sorti et fait tourner ma toupie : ils étaient subjugués ! Je crois qu’ils ont compris des « trucs », avec la toupie et avec la courbe elliptique. Bon évidemment, j’ai aussi parlé du théorème de Pythagore et du théorème de Fermat. C’est possible, mais il faut fixer le niveau.
AC – Je ne crois pas que ce soit une question de niveau. J’ai eu une expérience il y a longtemps avec Jean Petitot et Bernard Teissier. On louait un local où l’on faisait des réunions, pas avec des élèves, mais avec des biologistes, des philosophes, des littéraires, des gens qui n’avaient rien à voir avec les mathématiques et nous nous racontions mutuellement ce que nous faisions. Je me suis aperçu que c’est très facile de raconter des mathématiques très sophistiquées pourvu que l’on n’écrive pas 2 + 2 = 4 ou x + y = z. Si on écrit une équation, c’est fini, il n’y a plus personne. Mais par contre on peut raconter des idées de stabilité, de systèmes dynamiques, de topologie, d’ouvert, de fermé ; c’est tout à fait possible.
MA – On peut parler de phénomènes mathématiques sans l’écrire comme dans un article de mathématiques. J’ai eu des difficultés avec des magazines de vulgarisation qui souhaitent que les objets soient correctement définis. Si je veux parler de géométrie symplectique dans un article, « Pour la science » par exemple me demandera de définir cette notion avant d’en parler. J’ai eu beaucoup de difficultés avec eux pour cela. Je prétends que l’on peut définir un phénomène mathématique comme un phénomène physique. On peut décrire un phénomène, une idée sans avoir défini tous les objets rigoureusement avant.
AC – C’est parce que prendre contact avec des idées mathématiques ne demande pas des années d’expérience. Par contre, avoir des outils dans les mains qui permettent de travailler demande des années d’expérience. On peut donner aux gens des idées, mais on ne leur donnera pas un outil avec lequel ils pourraient eux-mêmes réfléchir.
MA – Si quelqu’un me demande ce qu’est un système intégrable, je demande :« Vous savez quoi ? ». Et ensuite j’essaye d’expliquer.
EV – Ta posture humaniste par rapport à la vulgarisation, penses-tu la partager avec bon nombre de mathématiciens ? Il me semble que les physiciens ou les biologistes sont vus par le grand public comme de bons vulgarisateurs. J’ai l’impression que peu de mathématiciens font cet effort de vulgarisation et que beaucoup le trouvent un peu vain.
MA –
Je
voudrai dire quelque chose à propos de cette apparente
facilité pour
vulgariser la physique. C’est un point de
désaccord dans mes relations avec
« Pour la science » ou
« La Recherche ». Il est souvent
considéré qu’un Boson W est un objet
plus concret qu’une forme symplectique.
Les éditeurs de revues de vulgarisation pensent que
l’on peut facilement en
parler alors que d’une forme symplectique, non. Je ne sais
pas à quel moment
cette idée est apparue. Un Boson W est évidemment
beaucoup plus abstrait qu’une
forme symplectique !
La différence entre « mathématiques » et « physique » dans le domaine de la vulgarisation ne me semble pas si évidente.
L’idée que les mathématiciens ne seraient pas intéressés par la vulgarisation de leur discipline vient aussi d’une certaine image que l’on avait des mathématiciens. C’est peut-être de moins en moins vrai.
EV – Tu constates dans ta pratique quotidienne que tes collègues consacrent une petite partie de leur temps (deux ou trois fois dans l’année par exemple) à essayer de vulgariser leur travail ?
MA – Par exemple pour la fête de la science à Strasbourg on a fait appel aux volontaires : tous les doctorants étaient volontaires et je crois que j’étais le seul professeur volontaire ! Il s’agirait donc d’une petite partie de mes collègues.
AC – Tout dépend de ce que l’on appelle vulgariser. Mais je suis frappé de voir que sur « Wikipedia » il y a beaucoup d’articles de mathématiques. Donc les gens éprouvent le besoin de raconter des mathématiques. Il y a des maths de tous les niveaux.
MA – Avec tous les niveaux de fautes !
AC – Il y a eu une étude statistique sur les fautes. Et il semblerait qu’il n’y ait pas plus de fautes sur « Wikipedia » que dans les autres encyclopédies ou bien dans les livres de maths. Ce qui est d’ailleurs assez rassurant.
MA – Je n’ai jamais corrigé d’article de maths sur « Wikipedia ». En revanche j’ai corrigé celui sur SK et j’ai mis mon livre en référence !
J’ai également
corrigé l’article sur Lebesgue. Il y avait
écrit : « Son père
était employé dans une
imprimerie ». Cela m’a
énervé ! J’ai
corrigé par : « Son
père était ouvrier dans une
imprimerie ». Lebesgue y attachait beaucoup
d’importance. Son père
n’était
pas un bourgeois… De temps en temps je vais
vérifier que personne n’a changé
cette phrase !
AC – Je crois qu’il y a un certain nombre de mathématiciens qui ont envie de partager leur travail. Justement parce que c’est beau. Quand on trouve de belles choses, on a envie de dire aux gens : « Regardez, c’est beau ; ne manquez pas cela ! ».
Les
Activités de
découverte
RC – Il y a une chose très encouragée en ce moment, y compris par les institutions, qui est de faire une place aux activités de découverte. L’idée est de mettre les gens dans des « situations de problèmes » variées qui ne demandent pas de connaissances préliminaires très importantes, mais qui nécessitent souvent des raisonnements assez sophistiqués et très jolis. On met alors l’élève ou l’étudiant dans la position d’un chercheur. C’est une chose qui est extrêmement favorisée aujourd’hui. Mais il y a une contrepartie à cela : le corpus des mathématiques lui-même est alors un peu sacrifié. C’est-à-dire que l’on donne aux gens des problèmes, mais on ne leur donne pas les outils qui forment un tout cohérent et qui permettent d’aborder autrement ces problèmes, autrement qu’un par un.
AC – Comment se fait-il que les Russes pendant très longtemps ont réussi à faire les deux. Vladimir Arnold a écrit son premier article à 17 ou 18 ans !
RC – Je sais bien. J’ai l’impression que l’on est en train de négliger l’enseignement des bases fondamentales. Il est vrai que cet enseignement était rebutant et ne marchait pas bien. On a donc choisi de développer l’esprit de curiosité et de découverte, en demandant aux élèves ou étudiants d’avoir une démarche de recherche, en montrant que l’erreur peut être féconde, etc. C’est très bien et j’y participe, mais…
AC – Ce n’est pas à un logicien qu’il faudrait dire cela : ne crois-tu pas que le problème n’est pas de mettre les gens dans une situation de recherche très tôt, mais plutôt la multiplication des options et la disparition d’un véritable corpus solide…
RC – C’est ce que je suis en train de dire. C’est lié.
AC – Quand il y avait maths 1- maths 2, méca-géné, les gens apprenaient des maths !
RC – Oui, mais le nombre de gens qui apprenaient des maths n’était tout de même pas très élevé.
AC – On va bientôt le joindre ce nombre ! Non ?
RC – Par ailleurs, c’est vrai. Mais ceci étant dit, il y a un défi qui à mon avis est loin d’être résolu : amener davantage de gens, et en particulier davantage de filles, à faire des mathématiques. Tout ce que vous décrivez sur l’intérêt que peuvent avoir des manifestations comme la « Fête de la science », les sites internet attirent certes des gens, on ne voit cependant pas de traduction de cet intérêt en matière de choix d’études. Ces études restent difficiles et la façon dont on est en train de les transformer n’est pas forcément une bonne réponse à cette question, puisqu’au fond on se dirige vers un programme d’enseignement extrêmement minimaliste. On diminue les notions de base que l’on enseigne au profit de ces activités intéressantes et ludiques mais néanmoins un peu marginales.
AC – Je crois que c’est un problème sociologique beaucoup plus vaste. Honnêtement, aujourd’hui il faut qu’un étudiant soit fou pour vouloir faire des études longues, difficiles et aléatoires, qui ne lui feront probablement pas gagner beaucoup d’argent ; ce dernier point étant tristement devenu le critère majeur de notre société.
Un livre « people » ?
RM – Michèle, que réponds-tu lorsque l’on te dit que c’est un livre très « people ».
MA – La seule personne qui pour l’instant a employé cette expression, c’est toi ! Donc je n’ai rien à dire là-dessus ! (Rires …)
AC – Moi, je ne dirai pas « people ». Les « people » ne savent pas qui est Calvino ou Perec.
RM –
Oui, on
pourrait dire « people »
raffinés ! Je pense que ce bouquin
s’adresse tout de même à des gens qui
ont une certaine maturité, une certaine
culture. Car les gens qui y sont cités sont connus
d’une petite élite, d’un
petit cercle. C’est d’autant plus vrai que
l’on a l’impression en lisant le
livre de rentrer dans leur club. On se sent un peu intelligent.
La
« Pathétique » -
Dostoïevski : amour de jeunesse
RM – Pour conclure, pourrais-tu nous dire deux petits mots de la « Pathétique » ?
MA – La Pathétique est donc une sonate de Beethoven (que précisément ma fille, qui est pianiste, jouait innocemment pendant que j’écrivais ce livre). Ce n’est pas la plus difficile, sans être toutefois facile.
Sophie était folle amoureuse de Dostoïevski quand elle avait 13 ans. Elle l’avait entendu dire un jour que c’était sa sonate préférée. Sophie étant une jeune fille de la bonne société jouait du piano (et parlait le français). Un jour, elle décida qu’à la prochaine visite de Dostoïevski elle lui jouerait cette sonate. Ce jour est arrivé ; il est allé dans le salon avec Anna (la sœur de Sophie) et elle s’est mise au piano pour jouer la « Pathétique » de tout son cœur. Mais au bout d’un moment, la pauvre Sophie réalisa que pendant qu’elle lui déclarait à sa manière son amour, Dostoïevski était en train de déclarer sa flamme à Anna deux pièces plus loin. Il n’avait probablement pas vraiment écouté ce qu’elle avait joué. C’est une histoire très pathétique ; elle était évidemment très malheureuse.
RC – Le début de la partition de cette sonate a été dans une première version manuscrite de ton livre.
MA – Oui. Mais il a été impossible de trouver une version libre. J’ai eu peur des problèmes de droits d’auteur.
RC – Il aurait peut-être fallu acheter les droits de publication. Elle était superbe…
MA –
Oui
c’est très beau une partition. C’est
comme une formule de mathématiques !
Un
secret
bien gardé
EV – Nous nous reverrons quand ?
MA – À la sortie de mon prochain livre !
AC – Il s’appelle comment ?
MA – C’est un secret !
RC – Joli titre !
Bibliographie
[Audin 2005]
Audin, Michèle, Géométrie, deuxième édition, EDP-Sciences, 2005.
[Berger 1990]
Berger, Marcel, Géométrie, Nathan Université, Collection : Sciences, 1990, 429 p.
[Byatt 2003]
Byatt, Antonia, Une femme qui siffle, Flammarion, Paris, 2003, Traduit de l’anglais par Jean-Louis Chevalier.
[Chenciner
2008]
Chenciner, Alain, Courbes algébriques planes, Springer, 2008, 160 p.
À l'origine paru dans Publications mathématiques de l'université Paris VII, 1978.
[Détraz 1993]
Détraz, Jacqueline, Kovalevskaïa, l’aventure d’une mathématicienne, Belin, Paris, 1993.
[Kovalevskaya 2004]
Kovalevskaya (Sophie), Une nihiliste, Phébus, 2004, préface de Michel Niqueux, Paris, 175 p.
Kozloff, Valeri, Sofya Kovalevskaya: A Mathematician and a Person, Russian Math. Surveys, 55, 2000, p. 1175-1192.
Annick Lesne, Jean-François Dars, Anne Papillault, Les déchiffreurs – Voyage en mathématiques, Belin, 2008.
[Singh 1999]
Singh, Simon, Le dernier théorème de Fermat, Hachette littératures, Collection Pluriel, 1999
Articles et conférences de Michèle Audin
- Le cas de Sophie Kowalevski, conférence "Un texte, un mathématicien" de la BnF
- Equations différentielles: le cas Cauchy - Kowalevski, conférence donnée dans le cadre du séminaire "Enseignement des mathématiques" de L'IREM Paris 7
- Le cas de Sophie Kowalevski, Tangente 109, mars-avril 2006 p 26-29
- Les deux idées de Sofia, Images des mathématiques, janvier 2009
- Autres articles et billets dans images des mathématiques

