Il n'y a que deux signes pour exprimer tous les nombres : 1 (
) et 10 (
)
59 chiffres
La numération est basée sur 59 « chiffres ». Ces chiffres sont écrits en répétant les 1 et les 10 autant que nécessaire (comme dans la numération égyptienne, par exemple)
unités :
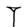
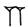
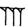
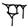
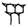
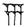
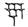
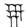
dizaines :
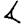
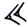
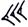
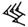
Exemple :
= 59
Base 60
La numération obéit à un principe de position à base soixante : le 1 (
) de chaque position vaut soixante fois plus que celui de la position précédente (à droite).
Exemples :
= 1.3 (1 soixantaine et 3 unités, soit 63 en numération décimale)
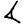
= 2.15 (2 soixantaines et 15 unités, soit 135 en numération décimale)
Virgule flottante
Il n’y a pas de signe pour le chiffre zéro. L’écriture cunéiforme des nombres positionnels n’indique donc pas l’ordre de grandeur, comme nous le faisons en écrivant des zéros pour distinguer une unité (1), une dizaine (10), un dixième (0,1). Le signe
peut désigner 2, ou 2×60, ou 2/60, etc. Les nombres sont donc définis à un facteur 60^n près, n entier positif ou négatif. Ce système est équivalent à ce que nous appelons aujourd’hui une écriture en « virgule flottante ».
Par exemple, le produit 9×20 de la table de 9 (voir les tables de multiplication) s’écrit 3, et non 3.0.
Exercice: écrire en base 60, à la façon des scribes, les nombres suivants.
100
120
600
1000
2007
245 466 735