Encart 2 : La généralisation de la condition R2
Nous
proposons de présenter la précision et la
généralisation faites par Du
Bois-Reymond et par Lebesgue
de la condition
d’intégrabilité R2.
| - Définition : Oscillation d'une fonction sur un
intervalle - Définition : Oscillation d'une fonction en un point - Un théorème de Du Bois-Reymond : Précision de la condition R2 - Un théorème de Lebesgue : Généralisation de la condition R2 |
Définition
(L’oscillation d’une fonction sur un
intervalle)
Soit
f une fonction bornée
définie sur un
intervalle I = [a,
b].
Alors l’oscillation de f sur l’intervalle I est :
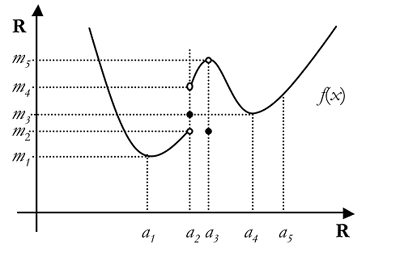Exemple :
Prenons le graphe de la
fonction tel que représenté sur la figure
ci-contre :
Alors,
nous avons les oscillations sur les intervalles suivants :
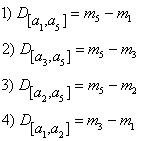
Du
Bois-Reymond précisa la définition
de Riemann
en
introduisant la notion suivante :
Définition
(L’oscillation d’une fonction en un
point)
Soit
une fonction f définie
sur un
ensemble E de nombres
réels et soit a un point
limite de E. Soit une suite {Ii}
d’intervalles qui
contiennent a et qui converge vers a.
Alors
Exemple :
En reprenant le graphe
de la fonction précédente, nous avons :
Du
Bois-Reymond précisa la condition R2 en
remplaçant la notion d’oscillation sur
un intervalle par la notion d’oscillation en un point.
Théorème
(Précision de R2)
Soit
f, une fonction bornée. Alors les deux conditions
suivantes sont
équivalentes :
R2 :
La somme des longueurs des intervalles où
l’oscillation de la fonction est
supérieure à σ
peut être rendue aussi petite que l’on veut.
Autrement dit :
R2’ :
L’ensemble G(σ)
des points où l’oscillation est plus grande que σ
est un groupe intégrable,
c’est-à-dire qu’il peut être
enfermé dans un nombre fini
d’intervalles dont la longueur peut être rendue
aussi petite
que l’on veut.
Pour les détails de la preuve, consulter les pages 27 à 29 de [Lebesgue, 1904].
Consulter
ce texte
(pdf, 4479 ko).
Finalement,
Lebesgue a
montré que
l’intégrabilité au sens de Riemann se
ramenait à des
considérations sur les points de discontinuité de
la fonction. En
fait, une fonction est discontinue en un
point si l’oscillation en ce point n’est pas nulle. De plus, il
généralisa la notion de groupe
intégrable en
remarquant qu’un groupe intégrable est un cas
particulier d’un ensemble de
mesure nulle. Voici
donc sa généralisation
de la condition R2.
Une
fonction bornée satisfait la condition R2, si
l’ensemble de ses points de
discontinuité est de mesure nulle,
c’est-à-dire qu’il peut être
enfermé dans un
nombre fini ou dénombrable
d’intervalles dont la longueur peut être rendue
aussi
petite que l’on veut.
Pour les détails de la preuve, consulter la page 29 et 109 de [Lebesgue, 1904].
Consulter
ce texte
(pdf, 4.479 Mo).
L’analyse de la preuve de Lebesgue nous permet d’affirmer que Lebesgue a trouvé une façon d’utiliser le résultat de Du Bois-Reymond pour faire cette généralisation; il a donc fait une généralisation conservative.