Dans ses Réflexions sur la cause générale des vents (1747), puis dans son Essai d'une nouvelle théorie de la résistance des fluides (1752), D'Alembert délaisse l'approche unidimensionnelle du parallélisme des tranches au profit d'une nouvelle méthode qu'il applique notamment, dans le second traité, à la mise en équation des écoulements plan (c'est-à-dire des écoulements supposés ne dépendre que de deux variables d'espaces). Il considère, pour ce faire, un élément de fluide infinitésimal rectangulaire $H$ (voir la figure 2a) et représente les deux composantes horizontale et verticale de la vitesse qui l'anime sous la forme de deux fonctions $p(x,y,t)$ et $q(x,y,t)$ dépendant continument des variables d'espaces $x$ et $y$ et de la variable temporelle $t$ (dans le cas compressible, la densité $\rho$ du fluide est de même mathématiquement définie comme une fonction de $x$, $y$ et $t$). Grâce à l'utilisation du calcul différentiel et intégral de fonctions de plusieurs variables ainsi qu'à l'application de son principe de dynamique, il lui est ainsi possible, comme nous allons le voir, de parvenir à des équations (aux dérivées partielles) beaucoup plus générales que ne l'étaient les équations différentielles ordinaires obtenues par le biais de l'hypothèse du parallélisme des tranches.

Figure b

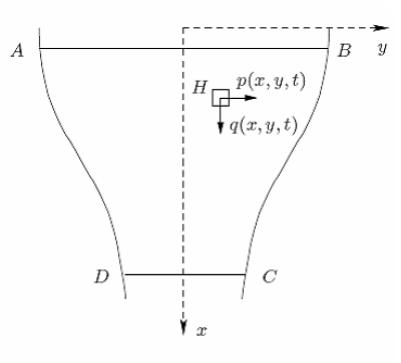Partant donc de cette représentation analytique du fluide et examinant un écoulement dans un vase ouvert en ses deux extrémités (voir la Figure b. ci-dessus), D'Alembert remarque que les composantes $p$ et $q$ de la vitesse répondent à la relation $\displaystyle{\frac{q(x,y,t)}{p(x,y,t)}=\frac{dx}{dy_{0}}}$
au niveau des parois du vase (avec $y_0$ l'équation, supposée connue, de ces parois), ce qui l'incite à y séparer les variables d'espace et de temps, c'est-à-dire à définir une fonction $\theta$ du temps $t$ telle qu'en tout point $(x,y)$ du fluide $p$ et $q$ vérifient :

$\displaystyle{p(x,y,t)={\theta}(t)p'(x,y)}$ 
$\displaystyle{q(x,y,t)={\theta}(t)q'(x,z)}$

Une telle hypothèse, ce dont D'Alembert est tout à fait conscient, équivaut à la considération d'un type particulier d'écoulement pour lequel les lignes de courant (définies par la relation $\displaystyle{\frac{dy}{p}=\frac{dx}{q}}$), dirions-nous en termes modernes, sont indépendantes du temps et confondues avec les trajectoires du fluide. La méthode dalembertienne de mise en équation du mouvement se décline dès lors en deux étapes.

La première, relative aux fluides tant compressibles qu'incompressibles --- nous nous placerons néanmoins dans le seul second cas de figure, ce qui revient à poser $\rho =1$ — consiste en la traduction mathématique de la conservation de la masse de l'élément de fluide $H$ entre deux instants successifs de son mouvement. Le fluide étant incompressible, et le mouvement s'effectuant dans le plan, la masse de toute partie du volume de fluide est donnée par son aire. La conservation de la masse revient donc à égaler l'aire $MO\times MN$ ou $dx\times dy$ de l'élément $H$ à l'instant $t$, c'est-à-dire l'aire du rectangle infinitésimal $MNQO$, et l'aire de ce même élément à l'instant suivant $t+dt$, c'est-à-dire l'aire $mo\times mn$ du rectangle infinitésimal $mnqo$ (voir la Figure c. ci-dessous).

Figure c

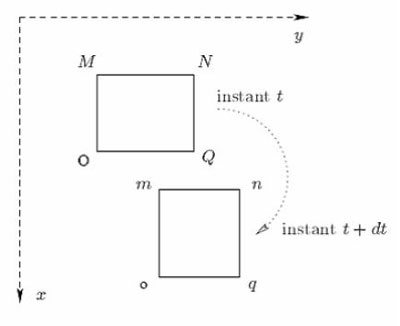Afin de parvenir à l'expression des quantités $mo$ et $mn$, D'Alembert a par ailleurs recours à la différentiation des fonctions $p$ et $q$, de telle sorte que (nous respectons ici les notations du XVIII^e siècle ; l'opérateur de différentiation partielle apparaît donc sous la forme $d$ au lieu de la notation actuelle $\partial$) :

$\displaystyle{mo=q(x+dx,y,t)dt=q(x,y,t)dt+dx\frac{dq}{dx}dt=\left(1+\frac{dq}{dx}dt\right)dx,}$
$\displaystyle{mn=p(x,y+dy,t)dt=p(x,y,t)dt+dy\frac{dp}{dy}dt=\left(1+\frac{dp}{dy}dt\right)dy}$

L'égalité des aires $MO\times MN=mo\times mn$ conduit alors, après avoir négligé les termes d'ordre $2$ en $dt$, à

$\displaystyle{dxdy=dxdy\left(1+\frac{dq}{dx}dt+\frac{dp}{dy}dt\right)}$,

c'est-à-dire

$\displaystyle{\frac{dp}{dy}(x,y,t)=-\frac{dq}{dx}(x,y,t)}$,

ou encore

$\displaystyle{\frac{dp'}{dy}(x,y)=-\frac{dq'}{dx}(x,y)},

compte tenu de l'opération de séparation des variables précédente. D'Alembert obtient ainsi sa première équation, aujourd'hui appelée équation de continuité ou équation de conservation de la masse d'un écoulement bidimensionnel stationnaire incompressible. Nous la trouverons couramment aujourd'hui sous la forme $\displaystyle{\nabla \cdot\mathsf{v}=0}$ avec $\displaystyle{\mathsf{v}=(q(x,y,t),p(x,y,t),0)}$ le champ de vitesse et $\nabla$ l'opérateur divergence.

La seconde étape de sa méthode de mise en équation, relative aux seuls fluides incompressibles, repose sur l'application de son principe de dynamique : en ramenant le problème à l'étude d'une situation d'équilibre, celui-ci lui permet d'avoir recours à la condition obtenue par Alexis Clairaut dans sa Théorie de la figure de la Terre (1743). Sachant, pour être plus précis, que cette condition d'équilibre s'écrit $\displaystyle{\frac{d{ R}}{dy}=\frac{d{Q}}{dx}}$
et fait intervenir les composantes horizontale ${ Q}(x,y,t)$ et verticale ${ R}(x,y,t)$ de la résultante des forces accélératrices s'exerçant sur l'élément $H$, D'Alembert se contente de leur substituer, d'après son principe, les forces accélératrices $F_y$ et $F_x$ perdues suivant $y$ et $x$ au cours du mouvement de l'élément entre les instants $t$ et $t+dt$.
$F_y$ et $F_x$ vérifieront donc l'équation $\displaystyle{\frac{dF_x}{dy}=\frac{dF_y}{dx}}$.        (7)
D'Alembert, pour aboutir à l'équation du mouvement, doit à présent parvenir à une expression analytique des deux composantes $F_y$ et $F_x$. Celles-ci correspondant à la résultante de la gravité (seule force extérieure s'exerçant sur le fluide) et des forces d'inertie, de telle sorte que

$\displaystyle{F_{x}=g-\frac{dq(x,y,t)}{dt}}$

$\displaystyle{F_{y}=-\frac{dp(x,y,t)}{dt}}$

D'Alembert procède à la différentiation des composantes $p=\theta p'$ et $q=\theta q'$ de la vitesse en considérant les variables d'espace $x$ et $y$ comme des fonctions de la variable temporelle $t$.

Il parvient ainsi à

$\displaystyle{F_{x}=g-\frac{d({\theta}(t)q'(x,y))}{dt}=g-\frac{q'd\theta +{\theta}dq'}{dt}=g-\frac{q'Tdt+{\theta}(Adx+Bdy)}{dt}}$
$\displaystyle{F_{y}=-\frac{d({\theta}(t)p'(x,y))}{dt}=-\frac{p'd\theta +{\theta}dp'}{dt}=-\frac{p'Tdt+{\theta}(A'dx+B'dy)}{dt}}$

avec $\displaystyle{{T=\frac{d{\theta}(t)}{dt}}, {A=\frac{dq'(x,y)}{dx}}, {B=\frac{dq'(x,y)}{dy}}, {A'=\frac{dp'(x,y)}{dx}}}$ et $\displaystyle{{B'=\frac{dp'(x,y)}{dy}}}$, système que l'on peut également, sachant que $\displaystyle{\frac{dx}{dt}=q=\theta q'}$ et $\displaystyle{\frac{dy}{dt}=p=\theta p'}$, exprimer sous la forme

$\displaystyle{F_{x}=g-\frac{q'Tdt+{\theta}(Adx+Bdy)}{dt}=g-q'T-{\theta}^{2}Aq'-{\theta}^{2}Bp'}$
$\displaystyle{F_{y}=-\frac{p'Tdt+{\theta}(A'dx+B'dy)}{dt}=-p'T-{\theta}^{2}A'q'-{\theta}^{2}B'p'}$

et conduit donc, compte tenu de l'équation (7), à

$\displaystyle{\frac{d(g-qT-{\theta}^{2}Aq-{\theta}^{2}Bp)}{dy}=\frac{d(-pT-{\theta}^{2}A'q-{\theta}^{2}B'p)}{dx}}$.

A cette équation aux dérivées partielles du second ordre caractérisant, en termes modernes, un écoulement à champ de force conservatif, D'Alembert préfère néanmoins une équation plus simple et moins générale,

$\displaystyle{\frac{dp'}{dx}(x,y)=\frac{dq'}{dy}(x,y)}$,

dont il se contente donc de montrer qu'elle y satisfait, restreignant ainsi son statut à celui de condition suffisante du problème. Il s'agit de la seconde équation du mouvement obtenue par D'Alembert dans son Essai d'une nouvelle théorie de la résistance des fluides. Elle s'écrit également $\displaystyle{\nabla\times \mathsf{v}=\mathsf{0}}$ en termes modernes (avec $\displaystyle{\mathsf{v}=(q(x,y,t),p(x,y,t),0)}$ le champ de vitesse et $\nabla$ l'opérateur rotationnel) et caractérise ce que nous appellerions un écoulement potentiel incompressible stationnaire idéal.

Dans son célèbre mémoire intitulé « Principes généraux du mouvement des fluides », présenté en 1755 devant l'Académie des sciences et belles-lettres de Berlin et publié deux années plus tard, Euler s'attaque aux écoulements tridimensionnels compressibles et considère donc un élément de fluide parallélépipédique animé d'une vitesse possédant trois composantes $q$ (suivant x), $p$ (suivant y), $r$ (suivant z) fonctions, comme la densité $\rho$, des trois variables d'espace $x$, $y$, $z$ et du temps $t$.

Généralisant la méthode mise au jour par D'Alembert au cas non stationnaire, Euler commence par établir l'équation de continuité ou de conservation de la masse et parvient, aux notations près, à

$\displaystyle{\frac{d\rho}{dt}+q\left(\frac{d\rho}{dx}\right)+p\left(\frac{d\rho}{dy}\right)+r\left(\frac{d\rho}{dz}\right)+\rho\left(\frac{dq}{dx}\right)+\rho\left(\frac{dp}{dy}\right)+\rho\left(\frac{dr}{dz}\right)=0}$,
que nous écririons également aujourd'hui
$\displaystyle{{\frac{\partial \rho}{\partial t}+\nabla\cdot (\rho\mathsf{v})=\mathsf{0},}}$
avec le champs de vitesse $\displaystyle{\mathsf{v}=(q(x,y,z,t),p(x,y,z,t),r(x,y,z,t))}$.

Pour parvenir à la seconde équation du mouvement, Euler opte en revanche pour une approche physique différente de celle de D'Alembert, fondée sur l'application de la seconde loi de Newton aujourd'hui connue sous la forme F = ma, où m et a correspondent respectivement à la masse et l'accélération de l'élément de fluide considéré, et F à la somme des forces qui s'exercent sur lui. Cette quantité $F$ regroupe non seulement la somme $f$ des forces extérieures (par exemple celle due à la pesanteur), de composantes $f_{x}$, $f_y$ et $f_z$, mais aussi la somme des forces internes exercées sur l'élément par les parties du fluide environnantes. Sa détermination requiert donc la prise en compte des pressions internes s'exerçant sur chacune des faces de l'élément de fluide. Là où le principe D'Alembert permet de faire fi des forces internes en équilibrant les forces accélératrices détruites, la formulation newtonienne des lois du mouvement à laquelle Euler a recours le conduit ainsi à introduire la notion de pression interne, représentée sous la forme d'une fonctions $P$ des trois variables d'espace et de la variable de temps. Il obtient, de cette façon, le système de trois équations

$\displaystyle{{f_{x}-\frac{1}{\rho}\left(\frac{dP}{dx}\right)=\frac{dq}{dt}+q\left(\frac{dq}{dx}\right)+p\left(\frac{dq}{dy}\right)+r\left(\frac{dq}{dz}\right),}}$
$\displaystyle{{f_{y}-\frac{1}{\rho}\left(\frac{dP}{dy}\right)=\frac{dp}{dt}+q\left(\frac{dp}{dx}\right)+p\left(\frac{dp}{dy}\right)+r\left(\frac{dp}{dz}\right),}}$
$\displaystyle{{f_{z}-\frac{1}{\rho}\left(\frac{dP}{dz}\right)=\frac{dr}{dt}+q\left(\frac{dr}{dx}\right)+p\left(\frac{dr}{dy}\right)+r\left(\frac{dr}{dz}\right),}}$


équivalent à la formulation moderne

$\displaystyle{{\frac{\partial \mathsf{v}}{\partial t}+(\mathsf{v}\cdot\nabla) \mathsf{v}=-\frac{1}{\rho}\nabla P+\mathsf{f}}}$

avec le champs de vitesse $\displaystyle{\mathsf{v}=(q(x,y,z,t),p(x,y,z,t),r(x,y,z,t))}$ et l'opérateur gradient $\nabla$. Nous reconnaissons là la fameuse équation d'Euler gouvernant l'écoulement d'un fluide parfait compressible, dont l'équation (7) de D'Alembert constitue un cas particulier.

Retour au sommaire

Retour à l'article