Comment rendre compte de l'écoulement d'un fluide à l'intérieur d'un vase ouvert ou percé d'un orifice en son fond ?

Dans l'Hydrodynamica, publiée en 1738, Daniel Bernoulli fournit une piste prometteuse par le biais d'une approximation unidimensionnelle due à Newton : l'hypothèse du parallélisme des tranches. Celle-ci consiste à diviser le volume de fluide CDLP s'écoulant dans un vase vertical en tranches horizontales (du type KZzk : voir la Figure a. ci-dessous) d'épaisseur infinitésimale et à supposer que chacune de ces tranches est animée par une même vitesse v, dirigée dans le sens de l'écoulement. Le fluide considéré par Daniel Bernoulli étant incompressible — c'est-à-dire de densité ρ constante, ce qui permet, comme il est de coutume au XVIII^e siècle, de poser ρ = 1 — , la vitesse v de chaque tranche sera liée à sa section y par la relation vy = Cste et ne dépendra donc que d'une seule variable d'espace : la hauteur x, dépendant elle-même du temps t, du fluide dans le vase. Combinée avec l'application d'un principe mécanique adéquat, cette hypothèse permet d'appliquer le calcul différentiel au mouvement du fluide et, ce faisant, de parvenir à une équation différentielle ordinaire, vérifiée par v, que les outils disponibles à cette époque permettent d'intégrer.

Figure a. 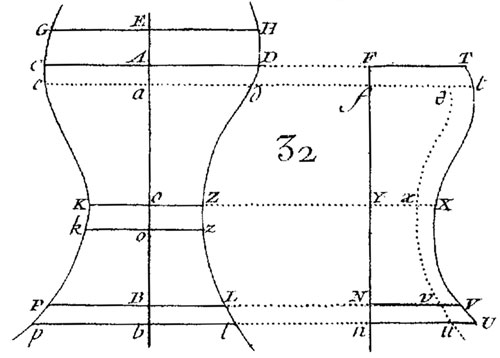Division du volume de fluide CDLP s'écoulant dans un vase vertical en tranches horizontales d'épaisseur infinitésimale du type KZzk.

Pour ce qui est du principe mécanique employé, D. Bernoulli a recours au principe dit de conservation des forces vives selon lequel la descente actuelle, c'est-à-dire la hauteur de chute du centre de gravité d'un système de corps soumis à la gravité, est égale à la montée potentielle, hauteur dont le centre de gravité remonterait si la vitesse de ces mêmes corps, supposés indépendants les uns des autres, était dirigée vers le haut. En termes modernes, la descente actuelle et la montée potentielle correspondraient respectivement à l'opposé de l'énergie potentielle E_p et à l'énergie cinétique E_c d'un système de corps soumis à la pesanteur, et leur égalité renvoie à ce que nous appellerions aujourd'hui la conservation de l'énergie mécanique — définie comme la somme de l'énergie cinétique et de l'énergie potentielle du système. Appliqué au mouvement de l'ensemble des tranches (de section y et d'épaisseur dx constituant le volume de fluide CDLP (de masse M), le principe de conservation des forces vives s'écrirait donc (nous respectons les notations de l'époque et ne faisons donc pas apparaître les bornes d'intégration ; elles correspondent néanmoins ici, comme dans toute la suite, à une variation de x comprise entre les hauteurs des surfaces supérieure et inférieure du volume de fluide CDLP) :

$\displaystyle{\frac{1}{M}\int{\frac{v^{2}}{2g}\cdot ydx}=\frac{1}{M}\int{x\cdot ydx}}$    (1)

Le premier terme correspond à la montée potentielle du système, le second à sa descente actuelle. Dans l'Hydrodynamica, D. Bernoulli ne raisonne pas directement sur cette équation, mais en considère une version différentiée entre les deux instants du mouvement précédant et suivant la sortie par l'orifice d'une masse infinitésimale de fluide afin d'être en mesure de parvenir à l'équation différentielle du mouvement.

D'Alembert, dans le Traité des fluides (1744), opte pour la même approche unidimensionnelle (fondée sur l'hypothèse du parallélisme des tran-ches), mais pour un principe mécanique différent : le principe de dynamique énoncé et déjà brièvement appliqué à l'écoulement d'un fluide à l'intérieur d'un vase dans la toute dernière partie de son Traité de dynamique (1743). Rappelons que ce principe permet de ramener un problème de dynamique mettant en jeu un ensemble de corps en interactions les uns avec les autres à un problème auxiliaire de statique : ainsi, comme l'explicite D'Alembert dans le Traité des fluides, « comme toutes les lois du mouvement des Corps Solides entre eux, ont été réduites par ce principe aux Lois de l'équilibre de ces mêmes corps, les Lois du mouvement des Fluides, peuvent aussi se réduire par ce même moyen aux Lois de l'équilibre des Fluides ».

Pour ce faire, D'Alembert considère le volume de fluide CDLP comme un ensemble de corps (les tranches) en interaction mutuelle, puis décompose, entre deux instants du mouvement t et t+dt, le mouvement gdt que chacune de ces tranches (par exemple la tranche KZzk de section de vitesse v à l'instant t et v+dv à l'instant t+dt) aurait reçu si elle se mouvait librement en deux autres : le mouvement dv réellement acquis par la tranche et le mouvement gdt - dv perdu ou détruit compte tenu de ses interactions avec le reste du système. Son principe assure dès lors que le volume tout entier serait à l'équilibre si chacune des tranches qui le compose n'était animée que par l'incrément de vitesse gdt - dv, ou par la force accélératrice $\displaystyle{g-\frac{dv}{dt}}$, lesquels seront donc perdus ou détruits au cours de l'intervalle de temps dt. Partant de là, il ne reste plus qu'à exprimer l'équilibre obtenu, ce que D'Alembert réalise en annulant le poids que la masse de fluide CDLP exerce dans son mouvement sur le fond ZC du vase, supposé immobile. Ayant établi que ce poids est proportionnel à la somme des forces accélératrices détruites dans chacune des tranches d'épaisseur dx du système, le savant en déduit l'équation

$\displaystyle{\int{\left(g-\frac{dv}{dt}\right)dx}=0}$     (2)

de l'écoulement du volume de fluide.

Nous verrons dans un instant comment s'écrit l'équation différentielle du mouvement correspondante. Avant cela, précisons néanmoins que, selon D'Alembert, « l'un des plus grands avantages que l'on tire de [cette] Théorie, c'est de pouvoir démontrer que la fameuse Loi de Méchanique, appellée la conservation des forces vives, a lieu dans le mouvement des Fluides comme dans celui des Corps Solides ». La critique s'adresse à D. Bernoulli qui ne donne pas, dans l'Hydrodynamica, de démonstration proprement dite du principe mécanique auquel il a recours.

La démonstration promise par D'Alembert consiste en une réécriture de son équation du mouvement (2) grâce à deux relations tirées du parallélisme des tranches et de l'hypothèse d'incompressibilité du fluide : la relation  yv = mu liant la section y et la vitesse v de la tranche quelconque KZzk avec celles, supposées connues, d'une tranche de référence GH et la relation  ydx = Cste. Sachant que $\displaystyle{dt=\frac{dx}{v}}$, c'est-à-dire $\displaystyle{dt=\frac{ydx}{mu}}$ compte tenu de la première des deux relations précédentes, D'Alembert parvient, d'une part, à $\displaystyle{\int{gdx}=\int{\frac{mudxdv}{ydx}}}$,
puis, grâce à l'application successive des deux relations, à $\displaystyle{(ydx)\int{gdx}=\int{ydx\cdot vdv}}$, soit $\displaystyle{(ydx)\int{gdx}=\int{ydx\cdot d\left(\frac{v^{2}}{2}\right)}}$.
Posant enfin $\displaystyle{N=\int{\frac{m^{2}dx}{y}}}$, et sachant que $\displaystyle{v^{2}=\frac{m^{2}u^{2}}{y^{2}}}$, il vient $\displaystyle{(ydx)\cdot g\cdot AB=d\left(\frac{1}{2}Nu^{2}\right)}$,
ou encore, puisque $ydx=\textrm{Cste}$, et posant $AB=x$ :

$\displaystyle{(CD\cdot Ff) \cdot gx=\frac{1}{2}u^{2}dN+Nudu}$     (3)

qui correspond à la version différentiée sur l'intervalle de temps dt de l'équation (1).

Pour parvenir à l'équation différentielle du mouvement, il ne reste plus qu'à obtenir une expression de la quantité dN. A l'instar de D. Bernoulli dans l'Hydrodynamica, D'Alembert s'appuie à cette fin sur un diagramme géométrique (voir la partie droite de la Figure a.) qu'il construit de la façon suivante : "imaginons [...] une Courbe TXV, dont les Ordonnées YX soient égales au quarré de la ligne constante $GH$, divisé par la ligne correspondante KZ, parallèle à GH ; & soit appelée N l'Aire de la portion FTVN, qui répond à une portion donnée CDLP de l'espace indéfini renfermé entre les lignes Courbes GKP, HZL". La courbe TXV ainsi définie est donc telle que $\displaystyle{YX=\frac{GH^{2}}{KZ}}$ et l'aire FTVN correspond bien à la grandeur $\displaystyle{N=\int{\frac{m^{2}dx}{y}}}$ dans laquelle, rappellons-le, m = GH.

Supposant que cd et pl sont respectivement infiniment proches de CD et de PL, et tels que $CDdc=PLlp$, la différentielle $dN$, telle qu'exprimée par D'Alembert, correspond à la différence entre les valeurs de $N$ aux instants $t+dt$ et $t$, c'est-à-dire à la différence entre les aires $ftUn$ et $FTVN$. La quantité $dN$ vérifie donc

$\displaystyle{dN=ftUn-FTVN=(ftVN+NVUn)-(ftVN+FTtf)=NVUn-FTtf}.

Sachant par construction que $\displaystyle{NVUn=NV\cdot Nn=\frac{GH^{2}}{PL}\cdot Nn}$ et $\displaystyle{FTtf=FT\cdot Ff=\frac{GH^{2}}{CD}\cdot Ff},$

et compte tenu de $CDdc=PLlp$, c'est-à-dire $Ff\cdot CD=Nn\cdot PL$, D'Alembert obtient : $\displaystyle{dN = NVUn-FTtf = \frac{GH^{2}}{PL}\cdot \frac{CD}{PL}\cdot Ff-\frac{GH^{2}}{CD}\cdot Ff = Ff\cdot GH^{2}\cdot \left(\frac{CD^{2}-PL^{2}}{PL^{2}\cdot CD}\right)}$.

Soient $k$ et $K$ les sections respectives des surfaces supérieure $CD$ et inférieure $PL$ du vase et $Ff=-dx$ (D'Alembert repère implicitement la hauteur $x$ du fluide par rapport au fond du vase, ce qui revient donc à orienter l'axe des $x$ dans le sens inverse de l'écoulement et explique l'apparition du signe " - " dans l'expression de $Ff$), l'équation (3) s'écrit donc

$\displaystyle{-kgxdx=-m^{2}\left(\frac{k^{2}-K^{2}}{kK^{2}}\right)\frac{u^{2}}{2}dx+Nudu}.

Elle correspond, aux notations près, à l'équation différentielle gouvernant l'écoulement d'un fluide dans un vase vertical de section variable obtenue par D'Alembert dans le Traité des fluides (livre II, art. 105) et par D. Bernoulli dans l'Hydrodynamica (section III, § 7).

Son application à la détermination de la vitesse de sortie $u$ d'un fluide s'écoulant dans un vase de section supérieure $k$ et percé en son fond d'un orifice de section $K$ nécessite ensuite de faire correspondre la tranche de référence $GH$ avec la tranche inférieure du volume de fluide en mouvement. Soit donc $GH=m=K$, la vitesse de sortie $u$ vérifiera l'équation différentielle

$\displaystyle{-xdx=\left(\frac{K^{2}}{k^{2}}-1\right)\frac{u^{2}}{2g}dx+\frac{N}{k}d\left(\frac{u^{2}}{2g}\right)}$      (4)

soit, sous une forme légèrement modernisée

$\displaystyle{x=\left(1-\frac{K^{2}}{k^{2}}\right)\frac{u^{2}}{2g}+\frac{N}{k}\frac{d}{dx}\left(\frac{u^{2}}{2g}\right)},

ou encore, en remarquant que $\displaystyle{\frac{d}{dx}\left(\frac{u^{2}}{2g}\right)=\frac{udu}{gdx}}$, c'est-à-dire $\displaystyle{\frac{1}{g}\frac{k}{K}\frac{du}{dt}}$ compte tenu de la relation $\displaystyle{\frac{dx}{dt}=\frac{Ku}{k}}$ :

$\displaystyle{x=\left(1-\frac{K^{2}}{k^{2}}\right)\frac{u^{2}}{2g}+\frac{1}{g}\frac{N}{K}\frac{du}{dt}}$      (5)

avec, rappelons-le, $\displaystyle{N=\int{\frac{K^{2}dx}{y}}}$.

Quoique D. Bernoulli et D'Alembert n'éprouvent aucune difficulté à intégrer (4) par quadrature, cette équation ne leur permet cependant pas de parvenir à une solution concordante avec l'expérience en dehors du cas où la section inférieure du vase ou de l'orifice percé en son fond est très petite en comparaison de sa section supérieure — ce qui équivaut à supposer $K$ négligeable par rapport à $k$. Cette hypothèse implique notamment, en termes modernes, la stationnarité ou quasi-stationnarité de l'écoulement (la vitesse du fluide ne dépend pas du temps $t$, de telle sorte que $\displaystyle{\frac{du}{dt}=}$ ou $\simeq 0$). L'équation (4), ou (5), conduit alors à la relation $u^{2}=2gx$ et contient donc une première démonstration rigoureuse d'un résultat bien connu depuis son énoncé par Torricelli à la fin de la première moitié du XVII^e siècle (l'écoulement correspondant porte d'ailleurs aujourd'hui son nom), résultat selon lequel la vitesse d'échappement d'un fluide par un vase percé d'un très petit orifice correspond à la vitesse acquise par la chute libre d'un corps tombé de la hauteur séparant l'ouverture de la surface supérieure du fluide.

Nous conclurons ce bref panorama de l'approche du parallélisme des tranches en notant que l'Hydrodynamica contient également une version embryonnaire de ce que nous appellerions aujourd'hui la forme stationnaire du théorème de Bernoulli, version dans laquelle D. Bernoulli se restreint en particulier, compte tenu de son approche globale du mouvement du volume de fluide, à la considération de la pression externe, c'est-à-dire de la pression exercée sur les parois du vase contre lesquelles s'opère l'écoulement.

Rappelons qu'en termes actuels, ce théorème stipule que pour un écoulement parfait (c'est-à-dire non visqueux) , incompressible et irrotationnel (la vitesse dérive d'un potentiel), la somme de l'énergie cinétique $\displaystyle{\rho\frac{v^{2}}{2}}$, de la pression $p$ et de l'énergie potentielle $\rho gx$ se conserve le long des trajectoires du fluide, de telle sorte que : $\displaystyle{\rho\frac{v^{2}}{2}+p+\rho gx=\textrm{Cste}}$.

Dans l'Hydraulica, publiée en 1743, Jean Bernoulli parvient à une généralisation au cas non stationnaire de la version du théorème énoncée par son fils Daniel, généralisation que nous retrouvons sous la plume de D'Alembert dans le Traité des fluides. Précisons, pour finir, que l'équation (4) renferme elle-même ledit théorème dans le cas non stationnaire, mais exprimé entre les surfaces supérieure et inférieure du fluide (les pressions extérieures exercées sur ces deux surfaces étant égales, elles n'y apparaissent pas).