Dossier de Bernard Vitrac sur les géomètres de la Grèce antique - Chapitre 9 :: Le renouveau d'Alexandrie à l'époque impériale

 Encart 1: "Calculer" les cordes 

Ptolémée construit ses tables de cordes à l'aide des quatre règles démontrées ci-dessous.


Règle 1: corde sous-tendue par l'angle supplémentaire

Soit AB une corde sous-tendue par l'angle AKB et AC la corde sous-tendue par l'angle supplémentaire. BC est donc un diamètre donc le triangle ABC est rectangle en A et, d'après le théorème de l'hypoténuse (Euclide, I. 47), on a :

CA² + AB² = BC². Comme BC = 120, BC²  = 14400.  

Si  on connait AB on peut donc calculer AC.

Règle 1 : cord (180° - α ) = √(14400 - [cord (α)]²) 

                         Retour article

                     Retour au sommaire



Règle 2: corde sous-tendue par l'angle moitié

Soit AB une corde et AC la corde sous-tendue par l'angle supplémentaire. On coupe l'arc AB en deux parties égales au point D. On veut calculer la corde BD, corde de l'angle moitié.

On place CE égale à CA, on joint DE et on mène la perpendiculaire DF.

Dans le triangle BCD, rectangle en D, la droite DB est moyenne géométrique des droites BC et BF (Euclide, VI. 8); 

donc DB2 = BC.BF. Or BC vaut 120.
Il suffit donc de savoir calculer BF. On vérifie facilement que les triangles ACD, ECD sont isométriques par construction. Donc AD = DE. Mais AD = DB par hypothèse; donc DE = DB et le triangle DEB est isocèle. Sa hauteur est aussi médiane; F est le milieu de EB donc CF est la demi-somme de CE et CB, c'est-à-dire de CA et CB (puisque CE = CA). La règle 1 permet de calculer CA. D'où CF, puis FB. On en déduit DB.

Règle 2 : cord (α/2) = √(60.[120 - cord (180°- α)]) 


     Retour article

Retour au sommaire



Règles 3 et 4 : corde sous-tendue par la différence et la somme de deux angles

Soit ABCD un quadrilatère quelconque inscriptible dans un cercle. Alors le produit des diagonales (Ptolémée dit le rectangle contenu par AC, BD) est égal à la somme des produits des côtés opposés (les deux rectangles contenus par (AB, CD) et (AD, BC) respectivement.

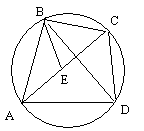
Soit E le point sur AC tel que l'angle ABE soit égal à l'angle DBC.

On vérifie que les triangles ABD, BCE sont équiangles donc semblables.

D'où : BC : CE :: BD : AD, soit : AD.BC = CE.BD  (*).

De même les triangles BAE et BDC sont semblables, d'où AB : BD :: AE : CD, 

soit AB.CD = AE.BD   (**).

En additionnant (*) et (**) : AD.BC + AB.CD = CE.BD + AE.BD = (AE + EC).BD = AC.BD.

A partir de là, si on se donne deux cordes AB, BC, on peut calculer les cordes sous-tendues par la différence ou la somme des arcs.

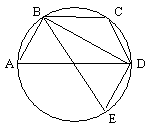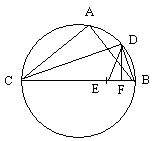
Cherchons, par exemple, AC. On mène les diamètres AD et BE. On a donc AB = DE et DE est connue.

Par la règle n°1 nous pouvons calculer BD et CE. D'après le théorème de Ptolémée appliqué à BCDE, on a : 

BD.CE = BC.DE + BE.CD.

Dans cette égalité BD, CE, BC, DE, BE sont connues. On en déduit CD.

De nouveau, par la règle n°1, on obtient AC.

Règle 3 : 120 cord (α - β) = cord (α). cord (180° - β) - cord (β). cord (180° - α)

Règle 4 : 120 cord [180° - (α + β)] = cord (180° - α).cord (180° - β) - cord (α).cord (β)


     Retour article

Retour au sommaire