Dossier de Bernard Vitrac sur les géomètres de la Grèce antique - Chapitre 4 : Euclide
Encart 2 : la structure des treize Livres des Éléments d'Euclide
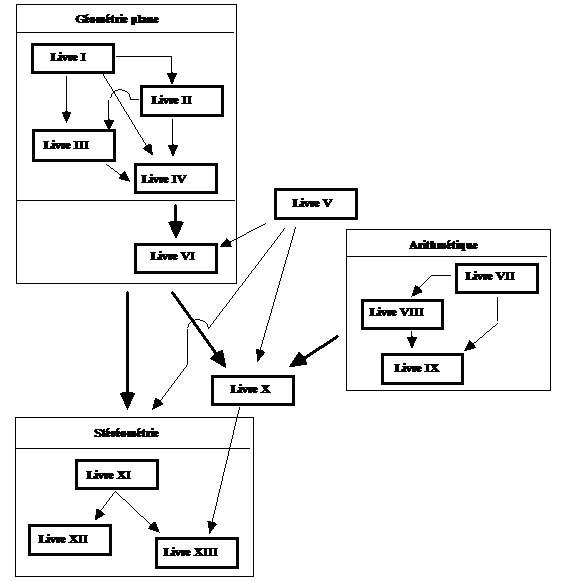
Structure globale des Eléments d'Euclide
Les flèches indiquent les liens déductifs ( en traits fins: de Livre à Livre; en traits gras: de sous-ennsemble à sous-ensemble)
Livre I
Constructions fondamentales. De l'égalité des triangles et des parallélogrammes
Livre II
Section d'une droite et égalités d'aires associées. De la quadrature d'une aire rectiligne
Livre III
Le cercle et ses segments. Tangence.
Livre IV
Des figures inscrites et circonscrites relativement à un cercle
Livre V
Théorie générale de la proportionnalité entre grandeurs
Livre VI
Des figures rectilignes planes semblables. De l'application des aires
Livre VII
Nombres entiers (PGCD, proportionnalité et rapports de nombres, PPCM)
Livre VIII
De la proportionnalité continue entre nombres. Nombres carrés, cubes, plans et solides semblables
Livre IX
Proportionnalité continue et nombres premiers. Théorie du pair et de l'impair. Nombres parfaits
Livre X
Commensurabilité et incommensurabilité des grandeurs. Classification de droites irrationnelles
Livre XI
Constructions stéréométriques fondamentales. Égalité et similitude des parallélépipèdes.
Livre XII
Pyramides et prismes. Proportionnalité dans les cercles, les cônes, les cylindres et les sphères
Livre XIII
Section en extrême et moyenne raison. Construction et comparaison des cinq polyèdres réguliers
.