Dossier de Bernard Vitrac sur les géomètres de la Grèce antique - Chapitre 4 : Euclide
Encart 1 : Le problème à trois ou quatre droites
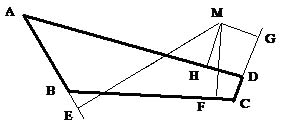
Soient quatre droites quelconques AB, BC, CD, DA et un point M. On mène à partir de M les perpendiculaires ME, MF, MG, MH sur ces quatre droites ou leurs prolongements.
Le lieu à quatre droites est l'ensemble des points M tels que le rapport ME.MG : MF.MH soit donné.
Ici ME, MF, MG, MH représente les distances du point M aux droites. Les géomètres grecs ne parlent pas du produit des distances mais des rectangles contenus par (ME, MG) et (MF, MH). S'il n'y a que trois droites, par exemple AB, BC, CD on impose que le rapport du rectangle (ME, MG) au carré décrit sur MF soit donné. Le point M satisfaisant cette condition appartient au lieu dit à trois droites. Ces deux lieux sont des coniques.
Dans la formulation qu'en donne Pappus le problème a été généralisé de différentes manières : d'abord on peut supposer que les droites ME, MF, MG, MH ne sont pas perpendiculaires mais menées à partir de M seulement sous des angles donnés. Cela ne change pas la nature des lieux. Ensuite on peut considérer davantage que quatre droites. Mais alors les lieux obtenus ne sont plus des coniques.
Ce problème est le premier grand problème que Descartes discute dans le I er Livre de sa Géométrie (1537).