Dossier de Bernard Vitrac sur les géomètres de la Grèce antique - Chapitre 3: La tradition mathématique alexandrine
Encart 1 : La mesure de la circonférence terrestre par Ératosthène
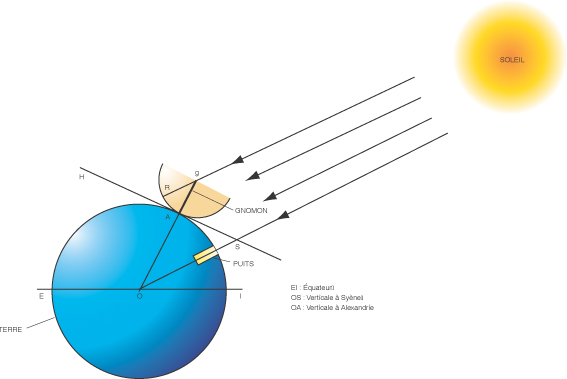
Le jour du solstice d'été, à Syène, quand le soleil est au méridien (midi), le fond d'un puits vertical est éclairé sans aucune ombre portée. Ératosthène en déduit que Syène est située sur le Tropique d'été.
Le même jour, à la même heure, l'ombre mesurée à l'aide d'un gnomon ajusté dans une demi sphère, AR, représente la cinquantième partie de la circonférence de ladite sphère.
Puisque le soleil est très éloigné de la terre, Eratosthène fait l'hypothèse que l'on peut supposer, pour simplifier, ses rayons parallèles. Il admet également que Syène et Alexandrie sont sur le même méridien, ce qui n'est pas tout à fait vrai.
Il en déduit (Proposition I. 29 des Eléments d'Euclide) que les angles RGA et AOS, alternes, sont égaux. L'arc AS est donc la cinquantième partie de la circonférence terrestre.
Sachant que la distance Alexandrie-Syène a été mesurée et vaut 5000 stades, il obtient donc 250 000 stades pour la circonférence terrestre. Comme il divisait le cercle en 60 parties (et non en 360°) il majora son résultat en adoptant 252 000 stades (soit 4200 stades par parties).
Plus que la précision toute relative du résultat — pour l'apprécier il faudrait connaître la valeur du stade utilisé (le stade athénien valait environ 178 m, le stade ptolémaïque 210 m) —, on admirera la simplicité de la méthode.